Théoriser un monde-Musique

à la lumière des mathématiques de Grothendieck (topos de faisceaux)

et à l’ombre de la philosophie de Badiou (Logiques des mondes)

(work in progress)

[ Programme de travail mamuphi (2008-2009) ]

Version fin décembre 2009

François Nicolas

Enjeux

1. Stimuler la théorisation de la musique à la lumière des « mathématiques fondamentales » (A. Connes) contemporaines et, ce faisant, consolider une ligne de partage des théorisations : pratiques théoriques musiciennes versus théories musicologiques [1]. Pour ce faire, après une pratique théorique convoquant la théorie mathématique de l’intégration pour théoriser l’audition et l’écoute musicales [2], une autre convoquant la diagrammatisation catégorielle pour théoriser le concert [3], je voudrais, à la suite de la semaine Grothendieck [4], convoquer la mathématique grothendieckienne des topos de faisceaux pour théoriser un monde-Musique.

2. Déployer cette pratique théorique de musicien à l’ombre de la philosophie, en l’occurrence celle d’Alain Badiou (Logiques des mondes). [5]

3. Objectif annexe plus pragmatique : s’approprier la théorie mathématique en question (celle des topos de faisceaux) en construisant un modèle musical, aussi systématique que possible (mais sans brutaliser notre domaine musical de référence…), qui mette à l’épreuve la série des concepts mathématiques enchaînés dans cette théorie [6]. On mesurera à cette occasion combien ce « recours » musicien aux mathématiques s’écarte méthodologiquement du rapport qu’un philosophe (tel Badiou) peut entretenir avec la même mathématique. [7]

Le programme initial était de dégager les réalités musicales susceptibles de constituer des interprétations pertinentes des notions mathématiques de faisceau, de site (de Grothendieck), de catégorie et de topos (de Grothendieck).

Si l’on diagrammatise ainsi le mouvement de pensée de toute pratique théorique musicienne :

le programme initial se présentait de la manière suivante :

Il y s’agissait donc de

1) formaliser un morceau de musique comme faisceau [8] des interprétations de sa partition,

2) formaliser la bibliothèque des partitions de musique comme site [9] de ses quodlibets,

3) formaliser le monde de la musique comme catégorie [10] puis topos [11] des morceaux [12] de cette bibliothèque,

4) examiner enfin les propriétés phénoméno-logiques du monde de la musique ainsi formalisé à l’ombre des concepts philosophiques de Logiques des mondes.

Au total, il s’agissait donc de constituer de toute pièce un modèle [13] musical possible pour la théorie mathématique existante des topos des faisceaux.

Assez vite, ce programme a buté sur sa troisième étape : formaliser une catégorie des morceaux de musique. À cette étape, en effet, le point décisif tient aux rapports musicaux entre morceaux susceptibles de constituer les morphismes de notre catégorie – une catégorie se constitue, à partir d’un diagramme d’objets, par une série de conditions sur les morphismes (plutôt que sur les objets [14]) - ; or il s’avère pour le moins difficile de formaliser mathématiquement les relations musicales entre morceaux (lors même que la formalisation de ces objets musicaux comme faisceaux ne pose par contre guère de problème).

Après différentes investigations, il s’est avéré nécessaire d’abandonner ce projet à sa troisième étape pour réaliser une conversion stratégique dont le principe est le suivant : on ne saurait construire une catégorie musicienne d’un monde-Musique par interprétation rigoureuse de la notion mathématique de topos, ni même par application du concept philosophique de monde (tel que déployé par Badiou dans Logiques des mondes ). Si le musicien veut soutenir l’idée musicienne d’un monde-Musique, il lui faut donc déployer à ses propres frais une catégorie spécifiquement musicienne de ce que « monde-Musique » veut dire.

Bref, le musicien doit assumer explicitement sa conception musicienne de ce que est un monde-Musique [15] sans pouvoir espérer la déduire (par projection) de la catégorie mathématique de topos ou du concept philosophique de monde.

Comprenons bien : un musicien ne partira pas d’un concept général de monde pour ensuite tenter de l’appliquer à la musique ; il s’agira plutôt pour lui de penser la musique comme monde-Musique en concevant cette expression « monde-Musique » comme un véritable nom propre composé.

D’où que notre schéma va s’avérer celui-ci plutôt que celui rapporté plus haut :

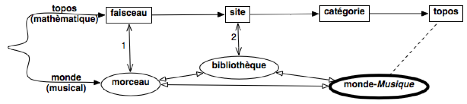
En introduction à ce travail, on esquissera cette problématique musicienne du monde, avant d’exposer les étapes 1 (faisceaux) et 2 (site) du programme initial.

On se contentera pour la suite de remarques plus éparses concernant un possible équivalent musical des objets caractéristiques d’un topos : initial, terminal, classifieur de sous-objets, limites et colimites…

Table des matières

I. Introduction 5

I.1 Une Idée musicienne du monde-Musique 5

I.2 Huit propriétés du monde-Musique 5

Remarque générale : les œuvres musicales proprement dites ne relèvent pas de ce travail. 8

I.3 Comment formaliser notre monde-Musique ? 8

II. Notations 10

III. Formalisation (1) : Le morceau musical comme faisceau 12

III.1 Cadre général 12

III.2 Topologie 15

III.3 Foncteur 16

III.4 Préfaisceau 16

III.5 Faisceau 17

IV. Premiers résultats musicaux 18

IV.1 Compte-pour-un 18

IV.2 Un type singulier d’un 18

IV.3 L’un d’un foncteur : la cohésion d’un morceau 18

IV.4 L’un d’un faisceau : la situation locale comme constituante 19

V. Formalisation (2) : la bibliothèque comme site 21

V.1 Cadre général 21

V.2 Topologie de Grothendieck 24

V.3 Site 25

VI. Seconds résultats 25

VI.1 Importance de la musicalisation incessante 25

VI.2 Importance du solfège dans la musicalisation 25

VI.3 Frontière mobile pièces/œuvres 25

VI.4 Importance musicienne des quodlibets… 25

VI.5 Statut musical d’une improvisation ? 26

VII. Simples notes mathématiques 26

VII.1 Objets 26

VII.2 Morphismes : hypothèse fondamentale d’une formalisation sans transposition 26

VII.3 Morphismes 27

VII.4 Limites/colimites 28

VII.5 Objets terminal/initial 30

VII.6 Sous-objets 32

VII.7 Foncteur représentable 32

VII.8 Catégorie de faisceaux 33

VII.9 Passage de la catégorie au topos 33

VII.10 Le classifieur de sous-objets Ω 33

VII.11 Les morceaux-limites 33

VIII. Notre monde-Musique à l’ombre de la logique philosophique 37

VIII.1 Préalables 37

VIII.2 Objet/sujet 37

VIII.3 Objet 38

VIII.4 Être & apparaître 38

VIII.5 Transcendantal (classifieur de sous-objets) 38

VIII.6 Matérialisme du silence musical 38

VIII.7 Conjonction et enveloppe 38

VIII.8 Dépendance et envers 40

VIII.9 Foncteur transcendantal 43

VIII.10 Points du topos 43

IX. Un monde-Musique 43

IX.1 Récapitulation 43

IX.2 « Monde » ? 44

IX.3 L’objectivation procède d’un monde-Musique qui constituant 45

X. Annexe : Discrétisation de la fonction interprétation I 45

XI. Notes de références bibliographiques 47

I. Introduction

I.1 Une Idée musicienne du monde-Musique

L’enjeu de ce travail est de bâtir une Idée proprement musicienne d’un monde-Musique.

· Pourquoi bâtir une telle Idée ? Car cette Idée occupe une place stratégique dans mon intellectualité musicale (ou Idéation musicienne de la musique).

Pourquoi une telle place stratégique ? Car s’y nouent les notions de logique et d’autonomie (auto-nomos) musicales, car s’y assure le principe : « la musique fait le musicien » (K. Marx) - non l’inverse [16] - car s’y joue la possibilité d’un art qui accède à une Idée et une pensée proprement musicales (où la musique ne se réduit donc pas, comme toute notre époque tend à nous le faire croire, au statut culturel et sensuel de la gastronomie et de l’œnologie [17]), un art qui donne droit à des œuvres musicales et valide le principe hégélien : « il y a des œuvres d’art ».

Dit autrement : il s’agit de soutenir, contre la doxa contemporaine « des musiques » - « à chaque dividu, à chaque communauté, à chaque culture sa musique » – qu’il n’y a qu’une musique au sens précis suivant : il n’y a qu’un monde de la musique, et ce monde est connexe (en droit, tout morceau de musique est susceptible d’intéresser tout autre).

· Comment bâtir une telle Idée ? La difficulté est ici patente : il n’existe pas de catégorie musicienne communément admise d’un monde, moins encore de la manière propre à la musique de faire monde. Mon hypothèse de travail est pourtant que chaque musicien sait bien, par sa pratique propre, que la musique fait monde, mais ce savoir pratique, empirique, communément partagé par tous les musiciens, n’a cependant pas de contrepartie notionnelle ou conceptuelle. Il existe bien un magazine intitulé Le monde de la musique mais ici l’expression ne touche au concept qu’au sens dévoyé que la publicité désormais lui donne ; au mieux le titre renvoie à l’idée platement sociologique qu’un monde de la musique se caractériserait… comme « monde des musiciens » [18].

Rien - à ma connaissance - dans les intellectualités musicales existantes qui permettent de s’orienter ; rien qui permette ne serait-ce que de s’attaquer au problème. C’est à tous ces titres qu’il importe ici de ne négliger ni la lumière des mathématiques, ni l’ombre de la philosophie.

Quelles sont les principales caractéristiques escomptées de notre monde-Musique ?

Quelle caractérisation axiomatique un musicien est-il en droit de donner du monde-Musique en sorte ensuite d’examiner l’adéquation ou non de cette catégorie musicienne spécifique (nom propre) à la notion mathématique (grothendieckien) de topos et au concept philosophique (badiousien) de monde ?

On se contentera ici d’esquisser la démarche, sachant qu’elle prend désormais place dans un vaste ouvrage dont le plan [19] pourrait être le suivant :

1) Les œuvres et l’écoute musicales : « L’œuvre agit la musique au fil d’une écoute. »

2) Le monde de la musique et ses morceaux : « la musique forme un monde à part entière » [c’est la partie en cours d’exposition dans la suite de ce texte]

3) Les musiciens et l’intellectualité musicale : « la musique fait le musicien, ce passeur évanouissant et pensif. ».

4) L’environnement du monde-Musique et ses raisonances (avec les mathématiques, les autres arts, la politique…) : « la musique ne pense pas seule ».

I.2 Huit propriétés du monde-Musique

Donnons, en première approche, huit propriétés qu’un monde-Musique doit assurer pour mériter – aux yeux du musicien - de s’appeler monde.

Précisons : ce travail s’inscrit dans l’édification d’une conception matérialiste et non anthropomorphique de la musique.

I.2.a Matérialité

On commencera par caractériser un point qui suffirait à lui tout seul à distinguer notre monde-Musique d’un topos stricto sensu : sa matérialité propre [20].

On posera que la matérialité de notre monde-Musique s’inscrit dans une dialectique entre matériau sonore et matière scripturale pivotant autour de la matérialité instrumentale d’un corps-accord (interaction d’un corps physiologique - celui du musicien - et d’un corps mécanique - celui de l’instrument de musique -).

La matérialité de notre monde ne tiendra donc ni à sa seule nature sonore (le son constitue le matériau musical) ni à la seule matière de la lettre (la note constitue la matière musicale) mais bien à leur dialectique via la matérialité instrumentale propre à la musique.

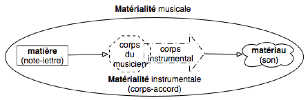
On voit d’ores et déjà que cette « matérialité » spécifique du monde-Musique n’a nul équivalent dans un topos. On va cependant voir – point suivant- qu’elle sert de base matérielle à la constitution musicale d’objets par découpage d’entités musicalement consistantes dans cette matérialité.

I.2.b Objets

Il s’agit maintenant d’examiner comment le monde-Musique va être constituant de ses objets.

Il y a en effet qu’un monde-Musique est fait d’objets qui lui sont propres ; mais un tel monde-Musique fait objet musical de « choses » (étants) qui composent sa matière particulière plutôt qu’il n’est fait par eux. Un monde-Musique est en capacité de constituer ses objets propres (musicaux) plutôt que d’être constitué par une récollection d’objets trouvés préexistants (par exemple sonores).

D’où la question stratégique : qu’est-ce qu’un objet musical ? Comment un tel objet musical est-il constitué par le monde-Musique à partir de sa matérialité propre (de « choses »), ou à partir d’objets sonores préexistants hors de ce monde ?

La réponse avancée sera ici : un objet musical est un morceau de musique. Et ce qui objective un tel morceau, ce qui découpe dans la matérialité musicale la figure spécifique d’un objet musical, ce qui transforme une simple chose sonore (éventuellement un « objet sonore » au sens de Pierre Schaeffer) en objet proprement musical, c’est l’opération spécifiquement musicale du solfège (de l’écriture musicale) – on sait, musicalement, qu’on ne transite pas des objets sonores aux objets musicaux et tout le Traité des objets musicaux de Schaeffer peut être vu comme l’exploration de cette impossibilité -.

L’enjeu sera donc de caractériser précisément ce qu’est un morceau de musique en sorte que le monde-Musique s’avère un monde des morceaux de musique, plutôt qu’une société des musiciens, une organisation des activités musicales, ou un système de notes et d’accords, etc.

C’est en ce point précis que la notion mathématique de faisceau nous sera d’une grande utilité : pour être un objet (musical), un morceau de musique doit d’abord être un objet ; on verra qu’il s’avère « un » au sens exact où un faisceau est lui-même « un » : un morceau de musique est le faisceau des interprétations d’une partition donnée.

I.2.c Relations

Un monde, c’est un ensemble dense et ordonné de relations entre ses objets. Ce n’est pas un paquet désordonné, un ensemble fourre-tout mais une mise en relation spécifique d’objets spécifiques.

Si la musique fait monde, il faut donc que les relations entre ses objets soient elles-mêmes musicales, appartiennent aussi à ce monde – et ne soient pas renvoyées à l’extériorité des relations humaines ou acoustiques ou techniques.

D’où la question : quelles sont les relations entre objets musicaux qui sont proprement musicales ? Là encore, un monde n’est pas l’incorporation de relations préexistantes extra-musicales mais l’institution d’un type nouveau de relations entre ses objets (entre les objets musicalement constitués). Par exemple, une relation musicale entre deux morceaux ne saurait être une simple relation de genèse musicienne (tenant au fait que tels et tels morceaux ont été produits par le même dividu) ; pas davantage une relation musicale entre morceaux ne saurait tenir à des propriétés strictement acoustiques, ou à telle ou telle propriété arithmétique. Par définition, une relation musicale tiendra à une logique musicale endogène : celle, par exemple, que met en œuvre cette pratique spécifiquement musicale du concert qui fait entrer plusieurs œuvres en résonance successive. Une relation musicale entre morceaux sera un type d’influence spécifiquement musicale entre morceaux.

En vérité, il ne faut pas concevoir musicalement qu’il y aurait d’abord des morceaux de musique puis des relations musicales entre eux : c’est d’un seul geste musical que morceaux et relations sont musicalement constitués par le monde-Musique (de même que dans une catégorie mathématique, l’identification des objets est inséparable de l’identification des morphismes qui les relient). Ceci veut musicalement dire qu’un morceau de musique n’existe jamais seul mais toujours en relation avec d’autres morceaux. Tout morceau de musique s’appuie sur d’autres morceaux qui lui préexistent et dont il reprend l’harmonie, la forme, les rythmes pour les varier. Tout morceau de musique existe enserré dans une réseau dense de relations musicales avec d’autres morceaux. Il s’agira donc d’examiner comment ce type musical de relations entre morceaux se laisse ou non formaliser dans le cadre des catégories de faisceaux.

I.2.d Compositions entre objets

Un monde, c’est la capacité de s’y déployer à l’infini sans en sortir par des opérations immanentes. Un monde est donc une instance de clôture sur soi.

Le monde-Musique est clos pour ses propres opérations (musicales). Il n’est bien évidemment pas clos pour des opérations mathématiques, acoustiques ou techniques – c’est-à-dire des opérations hétérogènes qui constituent des opérations sur les objets de monde plutôt que des opérations de ce monde - : par exemple, briser un piano, même pendant un concert, ne constitue pas une opération musicale mais une simple opération publicitaire amusicale (il faut ici récuser une fois de plus l’axiome nihiliste de Duchamp : ce n’est pas l’artiste – qu’il soit autoproclamé ou socialement proclamé – qui fait l’art).

Cette clôture sur soi du monde-Musique au regard de ses opérations propres concerne au premier chef les objets de ce monde : il s’agit ainsi de caractériser les opérations proprement musicales de fragmentation/récollection des objets-morceaux qui n’extranéisent pas les objets ainsi engendrés mais produisent de nouveaux objets musicaux (de nouveaux morceaux de musique donc) : il s’agit donc de légitimer respectivement la production d’« extraits » musicaux et celle de « pots pourris » ou de « recueils » de morceaux.

On examinera si ces opérations musicales ont des équivalents en matière d’opérations sur les faisceaux.

I.2.e Compositions entre relations

La clôture sur soi du monde-Musique doit valoir également pour ses opérations. Il nous faudra donc examiner ce qu’il en est des compositions possibles entre les relations musicales qu’on aura dégagées plus haut : comment se composent les « influences » musicales entre morceaux ?

Où l’on verra que cette composition musicale des relations musicales entre objets musicaux ne correspond pas exactement à l’axiomatique d’une catégorie (et donc a fortiori d’un topos).

I.2.f Logique

Un monde, c’est l’instauration d’une logique propre, immanente, autonome.

Un monde, c’est la capacité de prendre mesure propre et endogène de ce qui y compte, de l’existence : un monde-Musique, c’est la capacité de prendre musicalement mesure de l’existence proprement musicale. Un monde, c’est la dotation immanente d’un opérateur logique spécifique.

On posera qu’en musique, cet opérateur est le solfège, c’est-à-dire l’écriture proprement musicale. L’écriture solfégique – invention assez prodigieuse – dote la musique de cette capacité de mesurer ce qui du sonore importe musicalement. L’existence d’une écriture spécifiquement musicale centre le monde-Musique autour de principes logiques autonomes.

Il s’agira alors de prendre mesure de la consistance logique du solfège à la lumière de la notion mathématique de classifieur de sous-objets d’un topos.

Hypothèse décisive : le solfège construit un espace métrique (ℝ²) structurant une algèbre de Heyting ; il faut en effet concevoir la note de musique, au principe de ce solfège, comme désignant moins un point d’un espace qu’une famille d’ouverts (un ensemble mesuré de voisinages ouverts d’un point donné).

Dans la suite de ce texte, cette structuration du solfège comme algèbre de Heyting restera peu développée. Elle mériterait, à elle seule, tout un développement spécifique qu’on renverra ici à d’autres travaux mamuphi ultérieurs.

I.2.g Objets-limites

Un monde de morceaux de musique doit être en capacité de différencier les objets qui le peuplent du point des relations musicales qui les rapportent entre eux. Il doit être en état de typologiser les morceaux, en particulier d’identifier certains morceaux ayant dans ce monde-Musique une position exceptionnelle.

Le monde-Musique est ainsi doté de morceaux aux statuts spéciaux, d’objets-limites, par exemple de morceaux tels qu’en-deça (cf. Morton Feldman) ou au-delà (cf. Brian Ferneyhough) d’eux, il ne s’agit plus vraiment de morceaux de musique (d’objets musicaux) mais de simples objets textuels (cas pour Feldman) ou sonores (cas pour Brian Ferneyhough) : dans les deux cas, l’écriture musicale se dissout, soit vers le bas en écriture purement textuelle (« partitions verbales »), soit vers le haut en écriture purement numérique (« partitions informatiques »).

Il s’agira donc de spécifier deux types de morceaux-limites (minimaux et maximaux) par confrontation à la logique des objets-limites (injectives) et colimites (projectives) dans un topos.

I.2.h Le musicien, comme visiteur

Un monde, autonome par définition, n’est pas pour autant nécessairement autarcique. Un monde tolère d’être visité, parcouru sans pour autant qu’une telle visite constitue pour lui une menace de désagrégation.

On examinera en ce point le rôle dévolu au dividu musicien, lui dont le corps physiologique vient un temps animer un corps instrumental selon la logique proprement musicale d’un corps-accord.

On soutiendra que le musicien opère dans le monde-Musique non comme acteur de musique mais comme passeur évanouissant, comme une sorte de différentielle dans le calcul intégral d’une trace : il vient prêter temporairement son corps à une opération musicale immanente au monde-Musique. On relèvera combien cette opération proprement musicale a pour contrepartie nécessaire du côté du musicien, précisément « quand la musique s’arrête » (T. Heik) et qu’il se trouve décheté hors du monde-Musique, une pensivité spécifique.

*

Au total, matérialité, objets et relations, composition des objets et des relations, logique propre, objets limites et visiteur musicien constituent les huit propriétés au principe de notre Idée musicienne d’un monde-Musique.

Remarque générale : les œuvres musicales proprement dites ne relèvent pas de ce travail.

On n’abordera pas ici la question spécifique de l’œuvre musicale qu’on ne distinguera donc pas dans ce travail de la simple pièce de musique. On réunira les deux dans la notion englobante de morceau de musique : morceaux={pièces+œuvres}.

Philosophiquement dit, la question de l’œuvre renvoie à la figure du sujet en musique. Musicalement dit, elle renvoie à la figure spécifique de l’écoute musicale (par rapport à celle de la simple audition et de la perception).

On laissera ici cette question de côté sous l’axiome philosophique général qu’en musique comme ailleurs, le sujet est constitué et nullement constituant (en particulier de la phénoménalité) [21]. Cet axiome se dit musicalement : de même que c’est la musique qui fait le musicien (plutôt que l’inverse : le musicien fait de la musique, mais il ne fait pas la musique), de même c’est parce qu’il y a la musique, et donc des morceaux, bref parce qu’il y a un monde-Musique, qu’il y a des œuvres, et non l’inverse (les œuvres musicales ne font pas le monde-Musique : elles font l’art musical, ce qui est tout autre chose ; l’art musical est une partie du monde-Musique qui se distingue des régions formées comme simples cultures [22]).

I.3 Comment formaliser notre monde-Musique ?

I.3.a Morceaux-faisceaux

Notre problème de départ sera transposé de celui de Leibniz : un morceau de musique, pour être un morceau, doit être un morceau.

Hypothèse ici expérimentée : un morceau de musique fait un comme le fait un faisceau ; soit : le mode d’un du morceau de musique est formellement celui du faisceau.

Cette formalisation permettra de donner consistance à l’idée musicienne du morceau de musique comme unité objectale pertinente dans l’idéation musicienne de la musique. [23]

Question d’échelle

Comme on le reverra en cours d’exposition, il serait possible – comme René Guitart le suggérait déjà en 2002 - de formaliser une seule exécution-interprétation d’une partition donnée comme constituant déjà par elle-même un faisceau (auquel cas, un morceau de musique devient conçu comme topos de ces faisceaux-interprétaitons…).

On procèdera ici tout autrement, et ce pour des raisons proprement musicales : formaliser l’ensemble des exécutions-interprétations auxquelles une même partition peut donner lieu (en sorte de dégager l’un musical du morceau qui procède de cette partition) comme faisceau dote cet ensemble d’une structure supplémentaire, non transitive avec la structure topologique de la partition P sur lequel il se fonde. En effet, le concept mathématique de faisceau va ici attraper spécifiquement la structure musicale plurielle « des » interprétations (qui vont devenir les sections du faisceau) en sorte que la multiplicité du morceau sera désormais structuré selon deux niveaux hiérarchisés : le niveau de la multiplicité topologique que constitue une interprétation, et le niveau de la pluralité algébrique que constituent les interprétations-sections du morceau-faisceau.

Où se décide une question, essentielle dans tout processus de formalisation, qu’on dira celle de la bonne échelle, ici celle de savoir à quelle échelle musicale introduire le concept de faisceau. Comme on vient de le dire, on le fera ici à l’échelle du morceau de musique.

I.3.b Bibliothèque-site

Une fois clarifié ce qu’est un morceau, on se demandera : qu’en est-il d’un ensemble possible de ces morceaux de musique ?

Puisqu’un morceau est défini sur la base d’une partition qui lui est propre, il nous faudra examiner ce qu’il en est d’un ensemble de ces partitions. Soit la question de notre bibliothèque musicale.

Quelle structure lui donner ?

Notre hypothèse de travail sera de lui donner la structure d’un site, ce qui permettra de nous doter d’une bibliothèque « mobile » ou « ouverte » (au sens de « l’œuvre ouverte »). Il nous faut en effet autoriser que cette bibliothèque inclut d’une part tout extrait d’une partition existante et même tout pot-pourri ou quodlibet extrait d’une telle partition mais également tout recueil d’extraits, tout pot-pourri ou quodlibet prélevé dans l’ensemble des partitions de départ (celles des morceaux initialement répertoriés comme tels). Il faut ainsi qu’on trouve dans cette bibliothèque non seulement tous les morceaux du type « fantaisie sur les thèmes de Parsifal », « réminiscences de Don Juan », « paraphrases sur Rigoletto » mais également tous les recueils du type « classiques favoris », « le best of de Claude François », « les grands solos de Charlie Parker », « les grands chœurs des opéras de Wagner », « soirées de Vienne », « les mélodies traditionnelles de la Roumanie orientale », etc.

I.3.c Suites…

À partir de ce point, nous poursuivrons notre exploration du monde-Musique en nous détachant du chemin suivi par la mathématique, faute de pouvoir formaliser rigoureusement les relations musicales entre morceaux de musique (les morphismes entre objets).

On se contentera donc, à partir de là, d’incursions plus ponctuelles dans la mathématique des topos de faisceaux.

*

II. Notations

P : une partition

I : une interprétation-exécution

E : un enregistrement

S : un sonagramme

P [={P_i}] : ensemble (dénombrable) de partitions

I [={I_i}] : ensemble (dénombrable) d’interprétations-exécutions

E [={E_i}] : ensemble (dénombrable) d’enregistrements

S [={S_i}] : ensemble (dénombrable) de sonagrammes

I(P) : fonction interprétation I qui associe le sonagramme S à une partition P

ℐ(P) : Foncteur composé de la famille des fonctions I(P) pour une partition P donnée

ℱ(P) : ℱaisceau des interprétations I(P) pour une partition P donnée

Paramétrages

τ : paramétrage horizontal [0, 1] d’une partition-rouleau P

t(τ) : paramètre temporel d’une interprétation/enregistrement/sonagramme I/E/S

T : durée globale d’une interprétation/enregistrement/sonagramme I/E/S

T° : τ→t = fonction « tempo »

Sonagrammes

ƒ(t) : fréquence à l’instant t d’un sonagramme S

a(ƒ,t) ou a_τ(ƒ) : amplitude de la fréquence ƒ à l’instant t d’un sonagramme S(P) correspondant à l’instant τ de la partition P.

α : t→a(f) = fonction « amplitude »

i= αoT° : τ→a(f) = fonction « interprétation »

Topologie sur une partition

μ[P(∆τ)] : moment de la partition P (délimité par l’intervalle ∆τ) = un « ouvert » connexe

Q(P)=∑μ_i[P(∆τ_i)] : ouvert de P composé comme pot-pourri ou quodlibet tiré de P (non-connexe)

θ(P) : ensemble des ouverts de P (connexes ou non-connexes)

Bibliothèque

K : catalogue du présite ℘

Q(℘)=∑μ_i(P_j) : ouvert de ℘ (quodlibet) = série des moments μ_i des partitions P_j

ℬ [=℘_K] : bibliothèque (structurée comme site) des partitions cataloguées selon K,

Ⓜ : topos des faisceaux ℱ(P) sur ℬ , ou monde de la musique

Catégorie

M(P) : morceau de musique (« objet » de Ⓜ) conçu comme faisceau sur la partition P

m=m(M)=m↪M : sous-objet de M (ou sous-morceau)

S(M)= S↪M : moment de silence global du morceau M délimité par s⊂P

S(M) : ensemble des moments de silence global du morceau M

Topos

M_⓪=Ø : morceau initial (vide) [Stockhausen]

M_① : morceau terminal (entièrement silencieux) [Cage]

W=[0,1] : classifieur de sous-objets de Ⓜ

M_Ω : morceau étalon [Solfège]

ML : morceau-limite [Ferneyhough]

J(I)∈[0,1] : fonction justesse (ou exactitude) d’une interprétation conçue comme simple exécution (voir les morceaux-limites)

III. Formalisation (1) : Le morceau musical comme faisceau

Enjeu : formaliser qu’un morceau musical est un faisceau d’interprétations/exécutions [24], le faisceau des interprétations d’une partition donnée.

Une interprétation sera alors une section (globale) de ce faisceau [25].

III.1 Cadre général

III.1.a Idée directrice

Il s’agit de formaliser les différentes interprétations concevables d’une même partition donnée P.

On suppose ce faisant qu’il existe pour un morceau donné (mettons la Fantaisie op. 17 de Schumann) un partition canonique.

Ces interprétations de P sont dénombrables : soit I_i(P) avec i∈ℕ.

On formalisera chaque interprétation via un enregistrement E(I) puis un sonagramme S(E).

On fera les hypothèses (musicalement raisonnables) suivantes :

· à 2 partitions différentes correspondent des interprétations différentes : P≠P’ ⇒ I(P)≠I’(P’)

· à 2 interprétations différentes correspondent 2 enregistrements différents : I≠I’ ⇒ E(I)≠E’(I’)

· à 2 enregistrements différents correspondent 2 sonagrammes différents : E≠E’ ⇒ S(E)≠S’(E’)

· donc, par transitivité, à 2 partitions différentes ne peuvent correspondre que des sonagrammes différents : P≠P’ ⇒ S{E[I(P)]}≠ S’{E’[I’(P’)]}

Au total, on pourra donc discriminer les différentes interprétations d’une même partition P directement par leur sonagramme.

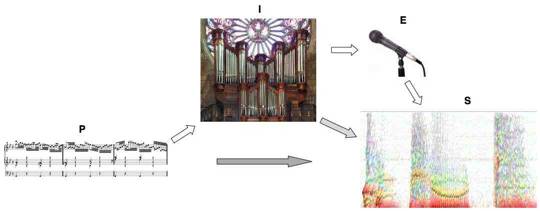
III.1.b Éléments

Soit une partition P paramétrable horizontalement par τ∈ [0,1] : on donne donc à notre partition la forme d’un rouleau d’un seul tenant, dévidable d’un bout à l’autre. Le paramètre est musicalement mesuré : par exemple par le nombre de mesures, de tactus ou d’impulsions élémentaires, ou encore par une distance en centimètres sur l’édition de référence (pour ne pas nous encombrer ici de problèmes d’ordre philologique, on suppose que la partition canonique est dotée d’une telle édition de référence).

Soit une interprétation I de cette partition P, fixée par un enregistrement E.

Cet enregistrement E peut se formaliser en un sonagramme S qui indiquera, pour chaque fréquence ƒ de l’instant t, une amplitude a(t,ƒ), cette amplitude se trouvant généralement représentée comme luminosité-couleur du point a.

Dans toute la suite (l’enjeu est ici une formalisation de pensée, pas la mise en place d’un dispositif computationnel), on supposera :

· que l’enregistrement E n’influe pas sur la compréhension de I, que E est techniquement neutre [26],

· que le sonagramme S n’influe pas sur la compréhension de E, que S est techniquement neutre [27],

· qu’il y a donc bijection stricte entre P={I} et S={S} via E={E} : I≅E≅S.

Par contre entre P={P} et I≅E≅S, il y a seulement surjection : pour tout P, existe au moins une I, un E et un S.

On parlera donc indistinctement d’une interprétation I pour désigner l’enregistrement E et/ou le sonagramme S.

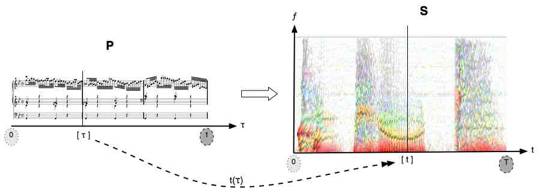
L’interprétation I(P) peut se formaliser en S[I(P)] selon la double application suivante :

· elle établit une bijection (continue et ∞-différentiable [28]) entre τ∈[0,1] de la partition P et t∈[0,T] de l’interprétation I (où T désigne le temps total de l’interprétation I) ; ceci formalise l’agogique propre de l’interprétation en question (tempo, rubato, dimension temporelle du phrasé…) ; appelons fonction tempo cette fonction T:τ→t ;

· elle associe à tout instant t de l’interprétation I (i.e. à tout instant τ de la partition P) et à toute fréquence ƒ du sonagramme S (ƒ∈ℝ⁺) une amplitude a(t,ƒ) – ce qui revient à dire qu’elle associe à tout instant t (i.e. à tout instant τ) une fonction (une courbe de relief, par exemple) a_τ(ƒ) de ℝ⁺ dans [0,1] [29] ; ceci formalise le reste de l’interprétation (hauteurs-timbre-accords et intensités…) ; appelons fonction amplitude cette fonction α : t→a(f) qui associe au nombre réel t la fonction a(f).

Soit la figure suivante :

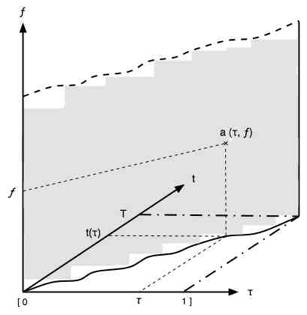
Le sonagramme S est ici représenté par un plan ondulé vertical où chaque point sera coloré selon l’intensité de son amplitude. Autre image : a désigne une « altitude » - ici horizontale - du point sur le plan ondulé :

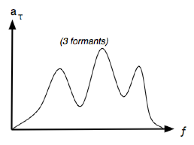
On peut référer directement a à τ plutôt qu’à t - soit la fonction a_τ(f) - puisque l’application τ→t est bijective (en même temps qu’elle est continue et ∞-différentiable).

Au total, appelons fonction interprétation la fonction I : τ→{t(τ),a_τ(f)}

On formalise ainsi une interprétation donnée I d’une partition donnée P (paramétrée horizontalement par τ) par la donation d’un sonagramme S c’est-à-dire la donation simultanée :

· d’une fonction bijective tempo t(τ) de [0, 1] sur un intervalle de ℝ⁺,

· d’une famille de fonctions amplitude α:τ →a_τ(f) de [0, 1] sur l’ensemble des fonctions réelles continues à valeur dans [0, 1].

On appellera donc I(P) [30] la fonction résultante : P→S qui associe à tout instant τ de la partition le couple des fonctions {t(τ),a_τ(f)}.

III.1.cDiscrétisation possible

On pourrait discrétiser cette fonction interprétation, somme toute comme le fait un interpréteur Midi d’une partition musicale.

On donne, en annexe finale, le principe d’une telle discrétisation qui, au point où nous en sommes, n’est pas décisive pour notre développement.

III.1.d Point de méthode essentiel

On admettra ici que les musiciens disposent de la capacité propre de trancher la validité ou non d’une I(P) donnée (c’est-à-dire d’un sonagramme-enregistrement-interprétation donné pour une partition donnée) : agogique valide (et donc durée T valide), exécution valide (en termes d’accord des instruments, de vibrato, de taux de fausses notes musicalement acceptables, et de dynamiques).

Rappel : la théorie mathématique des modèles suppose bien que le modèle est doté d’une règle de véridicité immanente (non formalisée : une sorte donc de boîte noire pour la théorie) apte à trancher sur la valeur de vérité (vrai ou faux) des formules du modèle.

Que la musique apparaisse pour partie aux mathématiques comme une « boite noire » (boite noire à l’intérieur de laquelle les musiciens, par contre, se meuvent en toute clarté) est essentiel : il ne saurait y avoir de transparence intégrale de la musique pour la mathématique, et ce pour des raisons philosophiques (la musique mobilise des sujets singuliers - les œuvres et les Œuvres - ; or la mathématique ne peut qu’ignorer le propre des sujets : tout au plus peut-elle radiographier leur être et l’être de leurs effets [31]).

Il y a donc tout lieu de se « méfier » d’une théorie mathématisée qui prétendrait formaliser un modèle musical dépourvu pour elle d’obscurités, de consécutions incompréhensibles, de liaisons opaques…

III.2 Topologie

Revenons à une interprétation I donnée.

Les ouverts qui vont être au principe de la topologie de P seront les intervalles de nature temporel : ∆τ désignera un intervalle horizontal (de « temps ») sur la partition.

III.2.a Remarque

On pourrait certes envisager de compléter l’intervalle « temporel » par un intervalle vertical ∆ƒ (un registre) de registres-fréquences. On aurait ainsi des parties-rectangles dans la partition. Mais il n’est pas possible, dans le sonagramme, d’isoler un intervalle de fréquences qui corresponde à un registre dans la partition : les harmoniques des sons se mélangent, et c’est précisément en la qualité de mélange que réside l’interaction musicale. On ne peut donc associer fonctionnellement un registre précis de la partition (un ∆hauteur) à un formant du sonagramme (∆ƒ).

Il nous faut ainsi travailler sur les seuls intervalles « temporels » : ce sont eux qui vont nous fournir la topologie naturelle de P.

III.2.b Ouvert de base : un moment

Si on dote ℝ de sa topologie naturelle (un ouvert de base est un intervalle ouvert), alors l’espace de départ P devient un espace topologique tel qu’un ouvert de base y est un intervalle de temps (∆τ).

Convenons de noter μ[P(∆τ)] un moment de la partition P défini par l’intervalle ∆τ

On notera θ(P) l’ensemble des ouverts de P.

Ce θ(P) constitue ipso facto une catégorie (dont les objets sont les ouverts et les morphismes les inclusions). P se trouve ainsi organisé en catégorie.

Une partie de P est donc, à la base, constituée d’un moment particulier de la partition.

On compose à partir de là des ouverts par les axiomes topologiques traditionnels pour les ouverts (intersection finie – union ad libitum). Ceci nous conduit à bâtir dune famille de pots-pourris ou quodliberts ouverts.

III.2.cQuodlibets…

La topologie d’une partition P s’édifie sur la base des intervalles ouverts ∆τ avec ∆τÌ[0,1] soit {∆τ}=P ([0,1]) – ensemble des parties de l’intervalle [0,1] -.

Un ouvert de P aura pour forme générale celle d’un ensemble de moments μ[P(∆τ)]. Appelons quodlibet un tel ensemble et notons-le Q(P). On écrira Q(P)=∑μ[P(∆τ_i)]=∑ μ_i

On retrouve ici cette vieille pratique musicale consistant à jouer des séries d’extraits d’un même opus, que ce soit pour des raisons didactiques ou pour des raisons de divertissement (songeons par exemple aux réminiscences, fantaisies, illustrations et paraphrases de telle ou telle œuvre chez Liszt).

Remarque

Un quodlibet étant défini par un ∑(∆τ_i) est un élément de P {P ([0,1])}.

Le nombre de quodlibets différents égale donc la cardinalité de P [P {P ([0,1])}]. Autant dire que notre base de travail est formellement infiniment infinie !

Remarquons cependant que musicalement, les choses sont beaucoup plus restreintes : l’infinité est ici plus formelle que musicale s’il est vrai que toute partition ne disposant que d’un nombre fini d’éléments, l’ensemble des intervalles ∆τ musicalement différents est en vérité fini. D’où que le nombre de quodlibets musicalement différents restera lui-même fini (mais bien sûr extrêmement grand).

III.3 Foncteur

Rappelons : une interprétation I fait correspondre à tout « point » de P (c’est-à-dire à tout instant τ) l’ensemble {t_τ, a_τ(ƒ)} d’un réel t_τ et d’une fonction continue réelle a_τ(ƒ) : ℝ→ℝ

À tout ouvert ∆τ de P, elle fera cette fois correspondre une fonction t(τ) et une nouvelle fonction a(τ,ƒ) : ℝ²→ℝ.

Un foncteur opère entre deux catégories pour y affecter tant les objets que les morphismes. Ici il va opérer de la catégorie θ(P) vers la catégorie Ens.

Un foncteur est « plus » qu’une fonction : il établit une correspondance non seulement entre des objets mais également entre les relations (de ces objets entre eux). Il opère entre deux catégories.

Ici, on peut dire musicalement que notre foncteur va identifier non plus, comme le faisait la fonction, la structure intérieure propre à chaque interprétation mais la structure de l’ensemble des interprétations. Le foncteur va donc concerner les rapports que les différentes interprétations-exécutions d’un même morceau entretiennent entre elles.

Il va transformer tout ouvert de P en un ensemble de fonctions-interprétations, et transformer toute inclusion d’ouverts de P (morphismes « topologiques » de type ↪) en morphisme contravariant entre interprétations. Il va ainsi opérer de θ(P) sur Ens.

Pour bâtir un tel foncteur, il nous faut passer d’une fonction à une famille de fonctions (et pour cela passer à l’espace de toutes les interprétations), famille qui va elle-même appartenir à une nouvelle catégorie en sorte que notre foncteur sera une correspondance entre la catégorie θ(P) et une région (celle de l’ensemble des fonctions continues ℝ⁺→ℝ⁺) de cette nouvelle catégorie : disons entre notre partition P et l’ensemble des exécutions musicales (i.e. musicalement valides) de cette partition.

On obtient ce faisant le Foncteur ℐ(P) des interprétations I (musicalement valides) de la même partition P qui, à tout ouvert ∆τ de P (« moment » de P) associe cette fois l’ensemble des fonctions (musicalement valides) {t(∆τ), a(τ,ƒ)}

Ce foncteur ℐ(P) est clairement contravariant sur un ouvert de P : V→U ⇒F(U)→F(V)

où V→U (parfois noté V↪U) correspond à V⊂U.

C’est un foncteur contravariant de la catégorie (espace topologique) θ(P) sur [une partie de] la catégorie Ens (constituée par l’ensemble des fonctions continues ℝ⁺→ℝ⁺).

ℐ(P) : θ(P)^op→Ens ℐ(P)∈ Ensθ^op

[ La catégorie fonctorielle obtenue est usuellement notée Ĉ=EnsC^op ]

Voyons maintenant comment ce foncteur ℐ(P) constitue un faisceau de fonctions sur P à valeur dans Ens, faisceau qu’on notera ℱ(P).

III.4 Préfaisceau

De manière assez immédiate, le foncteur ℐ(P) constitue un préfaisceau ℱ car il satisfait la propriété de restriction : toute réalisation sonore (sonagramme) valide d’une partie ouverte U de P constitue bien par excès une réalisation sonore (sonagramme) valide de toute partie V de U :

I(U) ∈ ℱ ⇒ I(V) = I|_V ∈ ℱ

(on retrouve simplement là le caractère contravariant de notre foncteur ℐ)

Rappel : on note indifféremment ici I(U), E(U), S(U) puisque interprétations, enregistrements et sonagrammes sont en correspondance bijective.

III.4.a Remarque

La restriction est transitive [a] : (f|v)|w=f|w

III.5 Faisceau

Ce préfaisceau ℱ est en fait un faisceau car il satisfait de plus la propriété de recollement : pour toute partie (ouverte) U de P et pour tout recouvrement (ouvert) U_i de U, si un ensemble d’interprétations I_i(U_i) est tel qu’elles coïncident sur leurs parties communes, alors il existe bien (dans le faisceau ℱ) une et une seule interprétation I sur U dont les restrictions coïncident avec les précédentes I_i sur les différents U_i.

Remarquons ici que cette propriété de recollement découle très directement du fait que les interprétations musicalement retenues (qui se situent au principe de cette formalisation) sont d’emblée des interprétations globales du morceau considéré (sans procéder ici d’une construction détaillée de proche en proche).

III.5.a Rappels

Cette propriété de recollement sur un préfaisceau ne va pas de soi : le point délicat tient ici [b] non pas à l’existence en soi d’un unique « recollement » mais au point de savoir si cet unique recollement – dont l’existence va de soi – appartient bien au préfaisceau ℱ des interprétations !

Cf. les contre-exemples élémentaires suivants :

· Un préfaisceau de fonctions constantes n’est pas un faisceau car une fonction « recollante » n’est plus une fonction constante.

· Le préfaisceau des fonctions continues bornées ℝ→U n’est pas un faisceau car une fonction « recollante » n’est plus bornée. [c]

· Soit un espace topologique T à deux points : T={x,y}. Soit le préfaisceau ℱ ainsi défini : ℱ(ø)=ø ; ℱ({x})=ℝ ; ℱ({y})=ℝ ; ℱ({x,y})=ℝxℝxℝ. Une restriction est une projection. ℱ est clairement un préfaisceau. Or une section globale sera déterminée par 3 nombres quand les valeurs des sections sur {x} et {y} n’en déterminent que 2 : on ne peut donc recoller de manière unique 2 sections sur {x} et {y}.

III.5.b Section

Une section du faisceau sur un moment U de P est une interprétation de ce moment.

III.5.cRemarque d’échelle

On aurait pu doter chaque interprétation d’une structure de faisceau puisque tout espace topologique est « faisceau-isable ».

L’idée aurait été la suivante : à tout ouvert ℴ de P on associe l’ensemble des fonctions t(τ) et a_t(f) corespondantes, et à toute inclusion d’ouverts de P (ℴ₁↪ℴ₂) on associe la restriction (contravariante) correspondante des fonctions t(τ) et a_t(f) : t₁(τ)→ t₂(τ) et a₁(f)→ a₂(f). On vérifiera facilement qu’un tel Foncteur contravariant constitue un faisceau (il est bien doté de la propriété de recollement).

Ceci dit, dégager la structure de faisceau d’une interprétation I donnée d’une partition donnée P ne nous apprend rien musicalement sur l’objet « interprétation » : la structure de faisceau reste ici purement formelle [32] à mesure précisément du point qu’elle ne fait que découler de la structure d’espace topologique de θ(P).

D’où qu’introduire le concept de faisceau à cette échelle serait, pour les buts proprement musicaux de notre formalisation, inutile et constituerait donc une simple pédanterie mathématique.

D’où qu’on réserve le concept de faisceau à la formalisation du morceau, ce concept de faisceau attrapant alors la pluralité spécifique des interprétations d’un même morceau.

La formalisation retenue structure topologiquement le multiple qu’est une interprétation et structure en faisceau la pluralité des différentes interprétations d’une même partition.

III.5.d Au total…

Au total un morceau-faisceau associe à l’indexation d’un rouleau-partition P selon l’intervalle [0, 1] un ensemble de rouleaux-sonagrammes :

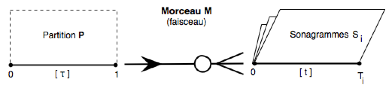
IV. Premiers résultats musicaux

On a donc établi qu’un morceau de musique est le faisceau ℱ(P) que composent les I(P). Un opus musical est un faisceau d’interprétations : un opus est le faisceau des interprétations musicalement concevables d’une partition donnée.

Il est clair que cette démarche met au cœur de la pratique musicale le rapport écriture-interprétations-perceptions [33].

Qu’est-ce que ce premier temps de cette pratique théorique permet de clarifier musicalement ?

Quel est l’intérêt proprement musical de cette formalisation ? Quel en est l’intérêt pour la musique ?

Rappel : on ne vise ici nulle implémentation calculatoire de la formalisation. Cette formalisation vise à à éclairer l’intellectualité musicale, à soutenir une Idée musicienne de la musique.

IV.1 Compte-pour-un

Un premier intérêt de cette formalisation est de donner forme à l’unité propre que constitue un opus musical : l’un d’un opus musical est ainsi formellement inscrit comme l’un d’un faisceau : le compte-pour-un de l’opus se fait sous le paradigme du faisceau.

Ceci lève l’hésitation traditionnelle à établir où se joue l’un d’un opus : est-ce dans l’unité finie d’une partition (auquel cas on s’affronte au problème : où est la musique si l’on s’arrête au niveau inaudible de la partition ?) ? Et s’il n’y a de musique qu’audible, faut-il alors compter pour un chaque nouvelle interprétation, poser donc qu’il y a non pas « L’ »Appassionata mais autant d’Appassionata différentes qu’il y en a d’interprétations contrastées ?

Le compte-pour-un en terme de faisceau stabilise ainsi le compte-pour-un de l’opus musical.

IV.2 Un type singulier d’un

Cette forme du compte-pour-un devient alors très précise (cf. les propriétés constitutives des préfaisceaux et faisceaux) : il ne s’agit pas seulement de compter-pour-un l’ensemble des interprétations. L’un d’un opus n’est pas seulement l’un d’un ensemble. Un opus n’est pas seulement l’ensemble des interprétations musicalement recevables d’une partition donnée. Cet ensemble est doté d’une structure particulière : celle de faisceau. C’est un ensemble structuré.

C’est précisément cette structure de faisceau qui va nous permettre dans la suite de construire des structures plus larges (en terme de topos) qui sont mieux formées ou informées que de simples notions d’ensembles. On ne se contentera pas de parler d’ensembles d’ensembles – ce qui ne spécifie pas grand-chose s’il est vrai que l’Être général n’est fait que d’ensembles d’ensembles ! – mais de faisceaux et de topos de faisceaux, ce qui nous fera travailler sur des structures géométrico-algébriques précises. C’est d’ailleurs ce qui nous permettra d’interpréter cette formalisation à l’ombre cette fois de la philosophie de Badiou, d’une philosophie non seulement de l’Être mais surtout – et ceci est forcément décisif pour la musique comme pour tout art – des phénomènes propres à l’apparaître (à l’être-là).

IV.3 L’un d’un foncteur : la cohésion d’un morceau

Il y a d’abord qu’un morceau de musique est un foncteur (rappel : un faisceau est un foncteur d’un type particulier).

Remarque : un foncteur transforme simultanément les objets et leurs rapports (morphismes) – ici à la fois les différents moments de P et leurs rapports – et structure donc à la fois l’ensemble des interprétations concevables d’un moment donné et les rapports entre différents ensembles d’interprétations pour différents moments.

La manière dont une exécution est ou n’est pas musicalement cohérente n’est pas ici formalisée. On admet que les musiciens disposent de leurs moyens propres pour trancher en matière de cohérence musicale face à telle ou telle fonction-exécution. On y reviendra : le fait que cette pratique théorique « économise » la formalisation proprement mathématique de ce type de relations musicales est essentiel et non pas contingent ; il en va là d’une dissymétrie constitutive du rapport entre un modèle et sa théorisation (au sens pris par ces mots dans la « théorie des modèles »).

Par contre, la cohésion entre interprétations différentes d’un même morceau est ici formalisée, précisément sous la notion de foncteur (puis de faisceau).

L’idée est donc la suivante : c’est le musicien, seul, qui tranche sur le fait que telle chose sonore est bien un objet musical recevable (en l’occurrence une exécution musicalement valide d’une partition donnée). C’est le musicien qui vient en gage de l’un de l’objet sans qu’il y ait lieu que la formalisation assure autre chose qu’en prendre acte.

Par contre, il est possible de formaliser certaines conséquences très particulières de ces actes musiciens en matière de cohérence : par exemple, si telle exécution de A est musicalement validée (décision musicale exogène), alors l’exécution qui en découle d’une partie B de A doit être musicalement valide (effet formalisé). Etc.

D’où que la formalisation concerne aussi certaines (pas toutes !) relations entre objets-exécutions, ce à quoi la notion de foncteur précisément nous sert.

Bref, ce qui fait qu’un morceau est bien « un », c’est un certain régime de cohérence entre exécutions musicalement valides : la notion de foncteur sert précisément à formaliser (à « attraper », à « fixer » dans l’écriture mathématique) cette cohérence (faite de relations entre objets).

IV.4 L’un d’un faisceau : la situation locale comme constituante

Un faisceau, c’est un foncteur spécifique. C’est une modalité particulière de l’un (du foncteur).

Un faisceau, on l’a vu, c’est une manière de faire-un à partir du local et « de proche en proche ».

Cette manière de faire-un nous intéresse musicalement car elle est analogue au travail musical qui s’approprie toujours une partition de proche en proche, de mesure en mesure, de page en page, de situation en situation, et ceci vaut tout autant pour le travail musical d’exécution et d’interprétation que pour le travail de l’écoute musicale (qui opère également « de proche en proche ») et pour celui de composition. C’est aussi à ce titre que la notion mathématique de faisceau est ici pour nous très éclairante.

On comparera ainsi deux interprétations d’une même partition [34] en priorité par confrontation de passages avant de pouvoir confronter les grandes architectures : ce qui légitimera que deux interprétations soient globalement différentes sera toujours enraciné en des différences d’abord locales, ne serait-ce que parce que l’écoute d’une interprétation donnée est toujours le résultat d’un recollement de proche en proche : on ne saurait écouter « d’un coup » une interprétation d’un bout à l’autre.

L’un du faisceau nous souligne que si un opus musical fait un, c’est donc d’abord parce qu’il est musicalement légitime de confronter localement différentes interprétations du même passage de la partition [35]. Et cela est légitime précisément parce qu’un opus n’existe réellement que lorsqu’un musicien prend en charge (en y prêtant un temps son corps, le temps de l’interprétation en question) cet opus de proche en proche et non pas globalement : bien des supposées « visions globales » d’un opus restent abstraites à mesure de ce qu’elles ne savent précisément pas se concrétiser localement, « de proche en proche ».

Plus généralement, il n’y a de vrai travail musical, y compris de composition, que « de proche en proche », ce qui n’est nullement déconsidérer l’approche globale d’une partition [36] mais simplement rappeler que cette globalité n’est ultimement jamais constituante : elle est constituée par ce qui occupe en musique la vraie position constituante et qui est la situation locale.

L’un d’un opus se constitue localement, et de proche en proche, nullement globalement puis par restrictions locales successives. Ainsi l’un de Tristan, ce n’est pas de prime abord sa vaste architecture de quatre heures (au demeurant forme en arche plutôt traditionnelle), c’est son début, étoilé du fameux accord qui rayonnera, de proche en proche [37] à grande échelle, c’est le renouvellement incessant de ces miniatures que Nietzsche avait bien saisies comme le vrai constituant de l’art musical wagnérien. Comme le moment-faveur de Farben, comme l’attaque de la première symphonie de Brahms, comme la fin de l’opus 11 n°3 de Schoenberg, l’accord de Tristan est le germe local d’un faisceau de points de vue musicaux à la fois différents et cependant localement enracinés en la même micro-structure écrite. L’un d’un opus musical procède bien d’un tel type de variété contrôlé localement bien plus qu’assuré globalement.

IV.4.a Constitution et détermination locale d’une interprétation

On peut soutenir techniquement qu’une interprétation est une fonction déterminée avant tout localement, aux deux sens suivants [d] :

1) si elle est musicalement valide sur un ouvert U (par exemple sur une mesure donnée), elle sera valide sur tout ouvert V partie de U (par exemple sur tout temps particulier de cette mesure) ;

2) si elle est musicalement valide sur un recouvrement U_i de U (par exemple sur toutes les mesures d’une section ou page donnée de la partition), alors il existe une et une seule interprétation musicalement valide de toute la page qui recolle ses interprétations partielles. Songeons par exemple ici au travail musical d’enregistrement d’une interprétation donnée qui va recoller une série de prises d’une partition dont on s’est assuré au préalable qu’elles sont compatibles sur les zones de recouvrement :

Au demeurant, cette appropriation par l’ingénieur du son d’une interprétation musicale (comme recollement d’une série de prises fragmentées et compatibles sur leur zones de recouvrement) correspond assez exactement à une compréhension de l’objet-interprétation comme Faisceau (voir plus haut la « remarque d’échelle »).

On pressent cependant que cette approche de l’interprétation comme faisceau relève d’une problématique plus technico-acoustique que musicale : disons qu’elle apparaît au moment de l’enregistrement d’une interprétation, au moment de construire une image de cette interprétation (sous l’hypothèse générale que la musique enregistrée constitue une image musicale, une image de musique plutôt que de la musique même).

On voit que, pour le musicien interprète, les choses se présentent un peu autrement : certes il ne jouera son morceau que de proche en proche – un musicien ne saurait jouer instantanément un morceau qui dure un certain temps ! – mais il va pour lui de soi qu’il dirige globalement son interprétation, qu’il porte aussi de proche en proche une vision globale du morceau et que cette vision globale ne saurait être la simple résultante d’un recollement : une interprétation, pour être musicalement valide, doit offrir une cohésion musicale globale, certes qui passe par le travail « de proche en proche » mais cependant ne s’y limite pas.

On dira : la possibilité pour l’ingénieur du son de recoller différentes prises partielles de manière musicalement significative (et pas seulement en s’assurant qu’il n’a pas de clic acoustique) tient ultimement à la capacité de l’interprète enregistré d’offrir une et une seule vision de l’œuvre à la fois.

D’où qu’on ne privilégie pas ici, pour des raisons musicales et non pas techniques, la formalisation d’une interprétation comme faisceau : c’est l’interprète qui assure musicalement que son interprétation sera un faisceau. Ou encore : si une exécution d’un morceau est musicalement validée (point de départ de notre formalisation), c’est parce qu’elle assure, a minima, qu’il y a bien recollement (c’est vraiment le minimum qu’on puisse exiger d’une exécution, après s’être quand même assuré qu’il n’y a pas trop de fausses notes !).

IV.4.b Perception locale et audition globale…

La pertinence du concept de faisceau pour formaliser ce qu’est un morceau musical se parachève ainsi : de même qu’un faisceau est une unité globale assurée de proche en proche, de même la validité d’une exécution donnée d’un morceau donné s’auditionne en intégrant de proche en proche (intégrale de Riemann ou de Kurzweil-Henstock) les données locales que constitue la perception. [38]

V. Formalisation (2) : la bibliothèque comme site

V.1 Cadre général

Nous avons vu comment une partition P engendre un ensemble d’interprétations I_i, et donc autant d’enregistrements E_i et de sonagrammes S_i :

P→I_iE_iS_i et donc P→S_i

où désigne un engendrement unique

Remarque

ne désigne pas ici un monomorphisme car les I, E et S n’appartiennent pas à une même catégorie.

ne désigne pas non plus ici un foncteur fidèle car les ensembles d’objets ℐ, ℰ et S ne constituent pas, a priori, des catégories (en tous les cas, on n’a pas ici défini de morphismes entre I, entre E et entre S qui permettraient de structurer ℐ, ℰ et S en catégories).

On a donc le diagramme suivant :

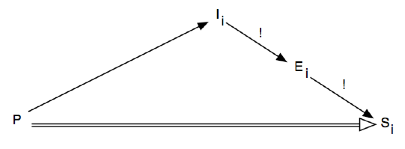
Demandons-nous maintenant, à l’inverse, dans quelles conditions il est possible de remonter d’une interprétation I donnée ou d’un enregistrement E donné à une partition P.

V.1.a Transcriptions

Premier cas : exécution

On posera qu’il est toujours musicalement possible de remonter d’une exécution musicale quelconque sur un instrument de musique quelconque à la partition implicite de cette exécution et ce par ce qu’on appelle musicalement une transcription. On remarquera que les différents dispositifs « midi » réalisent désormais automatiquement ce type de transcription.

On supposera qu’il est toujours musicalement possible de compacter les différentes transcriptions envisageables selon une seule partition canonique (face, par exemple, à différentes transcriptions du même solo de Charlie Parker, on compactera ces différentes transcriptions en une seule qui sera la plus détaillée).

On pose donc :

IP

Second cas : enregistrement sonore

On part ici d’un enregistrement sonore (par exemple d’un chant d’oiseau).

On posera que certains de ces enregistrements sonores peuvent être musicalisés au moyen d’une transcription qui prend musicalement mesure de sa structure sonore.

On supposera, comme précédemment, qu’on aboutit pour ces enregistrements (ceux que le musicien tient pour musicalisables), à une seule partition-transcription canonique dans le cadre logique de l’écriture musicale, disons du solfège (en entendant bien que ce solfège [39] a une historicité propre et qu’il évolue au fur et à mesure, précisément, des nouvelles tâches d’inscription musicale qu’il doit mettre en œuvre).

On pose donc :

EP

Remarque

On exclut ici toute écriture qui ne soit pas spécifiquement musicale. Par exemple le codage informatique d’un enregistrement par une série de 0 et de 1 stockés sur un CD n’appartient nullement à une telle écriture musicale. Au demeurant, un tel type d’écriture n’ouvre à aucune réinterprétation du texte, en raison précisément du caractère non musical de ce texte informatique.

On a donc ici les flèches suivantes

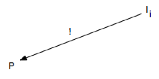
que l’on peut compléter alors des réinterprétations de la partition-transcription obtenue (comme par exemple les Double Six ont pu le faire pour quelques fameuses sessions de jazz…) dans le diagramme suivant :

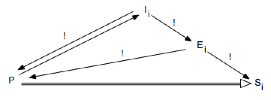
V.1.b Une bibliothèque

On va sur cette base constituer une bibliothèque P constituée de l’ensemble des partitions P existantes (ensemble dénombrable, potentiellement infini).

Cette bibliothèque regroupe les partitions existantes de tous les morceaux ou opus (pièces [40] & œuvres) de musique, qu’ils aient été dès le départ musicalement écrits ou que leur écriture procède d’une transcription.

P={P_i}

V.1.c Présite

Comment géométriser cet espace P de notre bibliothèque de partitions ?

Il nous suffit pour cela

1. de disposer d’une mesure uniforme pour toutes nos partitions. On rappelle que chaque partition a ici la forme d’un rouleau. Pour mesurer ces partitions-rouleaux, on retiendra naturellement le paramétrage, identique pour toute partition P, de son « temps » propre τ par l’intervalle [0, 1] : rapprocher différentes partitions au point τ = 0,33 reviendra à les examiner toutes au terme de leur premier tiers (spatialement mesuré) ;

2. de disposer d’un classement des partitions de notre bibliothèque, ce qui formellement ne pose guère de problèmes puisque l’ensemble des partitions constituant cette bibliothèque est dénombrable.

Au total, l’espace de notre bibliothèque est donc ainsi formalisable :

V.1.d Classement

Il faut ensuite choisir un ordre des partitions, sachant qu’en ce point, l’expérience musicale n’en impose guère qui soit canonique. Il y a donc, en ce point, un nouveau facteur subjectif qui va jouer : comment tel ou tel musicien va-t-il classer cette bibliothèque de partitions ? Une conséquence est qu’a priori, le topos des morceaux de musique auquel on va aboutir sera construit légèrement différemment par chaque musicien. Mais en vérité, tout ceci n’aura pas grande importance formelle (même si cette affaire de classement est par contre musicalement décisive) puisque les différents espaces obtenus (en variant dans la même bibliothèque l’ordre des partitions) s’avèrent formellement isomorphes en sorte qu’on pourra facilement transiter entre bibliothèques ainsi différemment ordonnées (toutes ces bibliothèques, différemment classées, étant en tout état de cause composées des mêmes partitions, canoniquement éditées).

V.1.e Remarque latérale : un fibré

Remarquons que notre bibliothèque est structurée comme un espace fibré : elle est le produit d’espaces topologiques.

Chaque partition-rouleau, dotée de sa topologie canonique, constitue une fibre P.

Notre axe vertical – catalogue dénombrable et ordonné - constitue la base du fibré, laquelle va relever d’une topologie discrète. Soit K le catalogue : K∈ℕ avec i∈[1,K] qui indexe la partition P_i. On a P={P_i}.

Le pied de la fibre P_i – ou projection sur la base K – est ici formalisé par le nombre i.

V.2 Topologie de Grothendieck

Pour constituer notre bibliothèque en site susceptible de constituer la base d’un topos, il nous faut maintenant doter ce site d’une topologie dite de Grothendieck.

Une telle topologie de Grothendieck vise à exprimer en termes catégoriels les propriétés des recouvrements topologiques en sorte de pouvoir doter une catégorie (faite d’objets et de morphismes, non d’ouverts et de fermés) de propriétés analogues à celles d’un espace topologique. En quelque sorte, il s’agit là de doter une catégorie d’un ersatz de topologie. Comme en fait notre bibliothèque est facilement topologisable, sa topologie naturelle va faire office de topologie de Grothendieck.

Mais rappelons d’abord le sens mathématique précis des notions ici nécessaires.

V.2.a Principe général

Définition d’un recouvrement ouvert dans un espace topologique

Soit les ouverts U de l’espace topologique T.

Un recouvrement ouvert associe à tout ouvert U de θ une famille d’ouverts {U_x} (où U_x⊂U) dite famille recouvrante C(U) telle que

1) U appartient à cette famille C(U).

2) L’union de recouvrants est un recouvrement de leur union.

3) La restriction d’un recouvrant est un recouvrement de la restriction.

On a alors les propriétés suivantes [e] :

· Cette famille C(U) inclut toute sous-famille qui recouvre U de manière plus fine.

· Cette famille C(U) recouvre également toute partie V⊂U.

· Si une famille d’ouverts O(U) génère un recouvrement de chaque partie U_x du recouvrement C(U), alors cette famille O(U) est aussi un recouvrement de U.

Les ouverts de notre topologie (par intervalles horizontaux dans les partitions) vont nous servir de base pour une telle topologie de Grothendieck sur notre bibliothèque exhaustive de rouleaux ou de feuillets.

Définition d’une topologie de Grothendieck

Une topologie de Grothendieck transpose ces propriétés à une catégorie [f] en remplaçant espace topologique T par catégorie K, ouvert U par objet a, inclusion U_x⊂U par morphisme a_x→a, C(U) par C(a), et nos trois propriétés précédentes par celles-ci :

1. Id_a : a→a∈C(a).

2. La composition de deux recouvrants est un recouvrement du composé.

3. Le produit d’un recouvrant est un recouvrement du produit.

Équivalences

Pour un espace topologique, un recouvrement topologique équivaut à celui d’une topologie de Grothendieck [g].

On transforme en effet facilement un espace topologique en une catégorie en transformant, à l’inverse de la transformation ci-dessus,

· ses ouverts en objets de la catégorie ;

· les inclusions ⊂ en morphismes ↪.

Il nous suffit donc de doter notre bibliothèque d’une topologie et de recouvrements ouverts pour transformer cette topologie (au sens traditionnel) en topologie de Grothendieck et par là transformer notre présite en site.

V.2.b Topologie naturelle

La topologie naturelle de la bibliothèque – espace fibré résultant – va être le produit de deux topologies, l’une horizontale (sur l’axe τ des partitions), l’autre verticale (sur l’axe - discret - du classement des partitions).

Des quodlibets

On a vu comment un ouvert d’une partition P était un quodlibet (série ordonnée de moments librement prélevés dans cette partition).

Étendons ceci à toute notre bibliothèque.

Un ouvert sera cette fois un quodlibet sur toutes les partitions Q_i composant la bibliothèque (et non plus sur une seule).

On écrira Q(P)=∑μ_i[P_j] : un ensemble de moments μ_i prélevés dans l’ensemble des partitions P_j.

Topologie discrète

Verticalement, la topologie de l’axe de classement des partitions sera la topologie discrète.

Rappel

Une topologie discrète compte tous ses éléments comme ouverts en sorte que toute partie y devienne un ouvert. C’est la topologie qui comporte le plus d’ouverts possibles.

Au total…

Au total, la topologie de P sera le produit des deux topologies précédentes.

Qu’est-ce alors, dans cette bibliothèque, qu’un ouvert pour cette topologie ? C’est un ensemble ad libitum de moments musicaux de longueurs arbitraires restant indexés de la partition dont ils sont extraits.

Notation

La bibliothèque P={P_i} munie de cette topologie sera notée ℬ (pour ℬibliothèque).

V.3 Site

V.3.a Recouvrements

La notion classique de recouvrement ouvert d’un espace topologique [h] suffit à constituer les recouvrements de nos ouverts de ℬ.

Notre topologie « naturelle » sur ℬ suffit donc à doter notre bibliothèque d’une topologie de Grothendieck et donc à constituer notre présite en site.

VI. Seconds résultats

Examinons les nouveaux « résultats » de cette « pratique théorique ».

Qu’est-ce que la constitution de notre bibliothèque musicale en « site » nous apprend musicalement ?

VI.1 Importance de la musicalisation incessante

D’abord que notre bibliothèque vit par incorporation incessante de nouvelles transcriptions et de nouvelles manières de transcrire. Il y a en effet un déplacement incessant des frontières du monde-Musique pour y incorporer de nouveaux types de sonorités, d’instruments, etc.

N’oublions pas non plus les territoires musicaux laissés en jachère puis abandonnés par la musique vivante (voir certains instruments - luth, orgue, … - et certains genres – parmi les différentes danses par exemple -). Une musique n’existe vraiment que rejouée : les enregistrements du passé sont des images de musique plutôt que de la musique vivante… Ce sont des photos de la musique du passé plutôt qu’une musique d’ici et maintenant.

VI.2 Importance du solfège dans la musicalisation

Cf. les enjeux proprement logiques de l’écriture musicale. Cf. les transformations et mutations de l’écriture musicale…

Cf. enjeu aujourd’hui : comment musicaliser l’écriture informatique ?

VI.3 Frontière mobile pièces/œuvres

Cette différence (interne au monde-Musique et non plus externe comme les précédentes) est subjective : on peut ainsi incorporer à un nouveau processus sujet (à une nouvelle subjectivation) - on peut musicalement subjectiver - ce qui jusque-là n’était qu’une simple pièce.

Réciproquement, une œuvre de musique peut être jouée, exécutée comme une simple pièce et être ainsi désubjectivée, réduite à un simple morceau de concours, numéro virtuose, pièce du répertoire, etc.

VI.4 Importance musicienne des quodlibets…

Cf. appropriation de la musique comme monde sous forme de libres et variés quodlibets, propres à chaque musicien (ex. séries de moments-faveur, de « beaux passages », de « classiques favoris »,…).

VI.4.a On ne sort pas du monde-Musique par fragmentation des morceaux

Noter aussi ce point : on ne « sort » pas du monde-Musique par fragmentation des morceaux puisque tout extrait, comme tout autre morceau, donne lieu à un faisceau qui appartient au même ensemble de faisceaux.

VI.5 Statut musical d’une improvisation ?

Qu’en est-il du statut musical précis d’une improvisation non enregistrée ?

C’est une chose musicale morte, qui a vécu seulement le temps de son exécution, qui peut laisser des souvenirs dans la tête des musiciens (des individus) mais qui, pour le monde-Musique, est morte. Pour le monde-Musique, cette chose a le simple statut d’une étincelle.

Le monde-Musique qu’on vise ici à formaliser inclut bien ce genre d’étincelles. Il faut donc tenir non pas exactement que ce monde est un topos (comme si tout ce qui n’avait pas le statut d’un faisceau – telle ou telle improvisation non enregistrée par exemple – ne pouvait y appartenir) mais qu’il a la structure d’un topos de faisceaux.

*

Nous avons successivement montré :

1) que l’opus musical est le faisceau des interprétations de sa partition ;

2) que la bibliothèque des partitions de musique est le site de ses quodlibets.

3)

La catégorie des faisceaux d’interprétations sur ce site va-t-elle constituer un topos de Grothendieck [41] ?

C’est très précisément en ce point que notre expérience de formalisation (bâtir un modèle musical à la théorie grothendieckienne des topos de faisceaux) doit se suspendre.

Contentons-nous à partir d’ici d’indiquer les étapes telles qu’elles étaient initialement envisagées.

VII. Simples notes mathématiques

Appelons Ⓜ le topos des faisceaux ℱ(P) sur ℬ

Voyons d’abord ce que veut dire que notre ensemble de faisceaux sur notre site ℬ forme une catégorie.

Nous verrons ensuite ce que veut dire que cette catégorie forme un topos.

VII.1 Objets

Nos objets sont nos faisceaux, c’est-à-dire les faisceaux d’interprétations d’un quodlibet (ou d’un opus) donné.

VII.1.a Notation

Notons désormais M (pour « morceau de musique ») un tel faisceau en tant qu’objet de Ⓜ.

On distinguera soigneusement le faisceau M de sa base scripturale P qui désigne la partition prélevée dans la bibliothèque ℬ.

M signifiera donc M(P), soit le faisceau des interprétations de la partition P.

Il va de soi que désormais nous ne ferons plus aucune différence entre partitions originelles et quodlibets bâtis sur le stock de partitions originelles. Rappelons : nous nous situons ici au niveau des morceaux de musique, non des œuvres musicales ; autant il serait aberrant de faire musicalement équivaloir Parsifal et un pot-pourri de ses « meilleurs moments », autant un quodlibet extrait d’études de Czerny constitue un morceau de musique à part entière.

VII.2 Morphismes : hypothèse fondamentale d’une formalisation sans transposition

Qu’est-ce qu’un morphisme entre de tels faisceaux : M→M’ ?

C’est un rapport entre deux faisceaux, donc pour nous entre deux « morceaux ».

Remarque : un morphisme de faisceaux est une transformation naturelle de foncteurs [i]. Si on l’appelle ∆:M→M’, il est tel que, pour V⊆U dans [0, 1], le diagramme suivant commute :

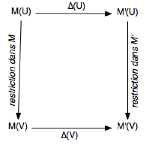
Quels rapports musicaux allons-nous ici prendre en compte ? La décision est d’importance : une catégorie est mathématiquement définie tout autant par ses morphismes que par ses objets - ainsi un même ensemble d’objets peut donner lieu à des catégories fort différentes selon les relations (entre ces objets) prises en compte.

VII.2.a « Influences » entre morceaux ?

A priori, nos rapports musicaux sont les rapports que les musiciens pratiquent et connaissent par leur travail propre : ce sont par exemple les rapports entre pièces et œuvres musicales qui sont pointés lorsque les musiciens parlent de l’influence de tel opus sur tel autre, de la différence entre une fugue et un rondo, etc.

∆:M→M’ formalise donc une influence donnée du morceau M sur le morceau M’.

VII.2.b Les trois axiomes des morphismes

On appliquerait alors à ces morphismes-influences les trois axiomes présidant à l’organisation des morphismes dans une catégorie :

Composition des influences

Si M influence M’ et M’ influence M”, alors M influence également M” : M→M’ et M’→M” ⇒ M→M” au sens où M influence M” via M’ (mais pas forcément directement).

Cette règle semble musicalement acceptable.

Associativité des influences

M→(M’→M”→M’’’)=(M→M’→M”)→M’’’

Cette règle est musicalement beaucoup moins évidente : il ne va pas musicalement de soi que l’influence indirecte de M sur M’’’ via M’ et M” ne dépende pas de l’ordre dans lequel les influences directes de proche en proche sont regroupées, compactifiées.

Identités

Il y a pour tout morceau M, une influence du morceau sur lui-même : Id(M) :M→M.

VII.2.c Difficulté

Au total, on pressent la difficulté : ce type d’influences entre morceaux, qui fait la vie même du working musician, n’est pas facilement « objectivable » (comme le morceau a pu l’être, en particulier grâce à cette base matérielle que lui constitue sa partition).

VII.3 Morphismes

Rappelons ici les principales distinctions catégorielles faites en matière de morphismes.

VII.3.a Monomorphismes/épimorphismes/isomorphismes

Il s’agit ici de la généralisation des injection/surjection/bijection traditionnelles.

Injection : f(a)=f(b)⇒a=b a≠b⇒f(a)≠f(b)	Injection catégorielle : ƒog=ƒoh ⇒ g=h	Monomorphisme (conserve les différences) noté « ↣ » ƒog=ƒoh ⇒ g=h simplifiable à gauche
Surjection : ∀b $a:f(a)=b	Surjection catégorielle : ∀g $h:ƒoh=g	Épimorphisme (préserve les identités) noté « ↠ » goƒ=hoƒ ⇒ g=h simplifiable à droite
Bijection : a=bÛf(a)=f(b) a≠bÛf(a)≠f(b)		Isomorphisme goƒ=Id(a) / ƒog=Id(b) noté « ↔ »

VII.4 Limites/colimites

Limites à gauche (projectives) / Colimites à droite (injectives)

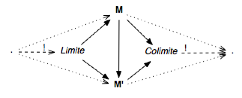
Rappel : « ! » désigne l’unicité du morphisme.

VII.4.a Exemples

a. Produits/sommes

Les produits (MxM’) et sommes (M+M’) :

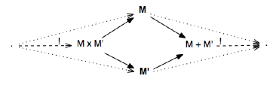
b. Égalisateurs/coégalisateurs

Les limites et colimites du diagramme à deux flèches

f°e=g°e… / c°f=c°g…

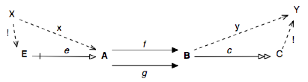
c. Produits fibrés [42] / sommes amalgamées [43]

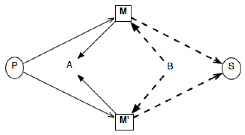
VII.4.b Projectif/injectif en musique ?

Peut-on transposer en musique ces deux notions de limites projectives et injectives ?

Suggérons deux premières possibilités de faire raisonner en musique le couple catégoriel projectif/injectif..

En matière de développements thématiques…

On peut distinguer un thème projectif (correspondant à la situation du développement musical classique) d’un thème injectif (une sorte alors de co-thème correspondant à un co-développement musical) où le thème n’apparaît qu’à la fin du développement (et non plus en son entame) : voir, par exemple, la Fantaisie et fugue pour orgue sur « Ad nos, ad salutarem undam » (1850) de Franz Liszt ou le premier choral pour orgue (1890) de César Franck…

On posera donc que chacun de ces deux morceaux produit sa propre limite injective sous forme respectivement des sous-objets-morceaux suivants :

Liszt

Franck

La polarité Rythme/Timbre

On pourrait considérer que la synthèse qu’opère le rythme est plutôt projective alors que celle que réalise le Timbre est plutôt injective :

· on déduit en effet un motif rythmique par la consécution de ses durées ;

· on induit par contre un Timbre-fusion à partir de ses partiels (on remonte des partiels vers le Timbre global et on ne saurait, à l’inverse, déduire d’un Timbre ses partiels).

On verra plus loin comment affiner cette problématique.

VII.5 Objets terminal/initial

VII.5.a Objet terminal ①

Généralisation du singleton : M①

① est donné par ①(M)={Ø} soit un singleton.

Le foncteur terminal d’une catégorie fonctorielle est le foncteur qui associe à tout objet le singleton. [j]

Faisceau-morceau terminal

On posera que M_① est un morceau silencieux (mettons 4’33” de Cage… [44]) en sorte qu’il n’y en ait qu’une interprétation concevable. M_① désigne donc ici la classe d’équivalence des morceaux entièrement silencieux, c’est-à-dire dont les partitions n’inscrivent que des lettres de silence, ce qui est rigoureusement isomorphe au morceau n’inscrivant qu’une seule lettre de silence : Œ

On l’inscrira du mathème suivant : = Œ

M_①= Œ [ ≡4’33” ou Cage ]

VII.5.b Objet initial ⓪

Généralisation de l’ensemble vide Ø : ⓪M

Le foncteur initial d’une catégorie fonctorielle est le foncteur constamment vide. [k]

Faisceau-morceau initial

C’est le morceau vide M_⓪=Ø vide (et non plus musicalement silencieux), soit cette fois celui qui procède d’une partition vide de tout signe musical et non plus de la partition d’un simple silence musical (M_①) d’une simple feuille de papier réglé : ===

On pensera en ce point à ce qu’on a pu appeler dans les années 60 les « partitions verbales » (et qui, à proprement parler, n’étaient plus des partitions puisqu’elles étaient précisément vides de tout signe musical). Sachant que l’objet initial est unique « à un isomorphisme près », on élira comme représentant de cette classe d’équivalence des « partitions verbales » vides Aus den Sieben Tagen de Stockhausen en raison à la fois de l’éminence du compositeur et de sa date de rédaction (mai 1968) et on inscrira :

M_⓪=/===/ [ ≡ADST ou Stockhausen ] [45]

VII.6 Sous-objets

Un sous-objet m du morceau M sera, par définition, une classe d’équivalence dans les monomorphismes de cible M (↣M) : m↣M.

On peut le caractériser par le produit fibré suivant :

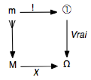
Un sous-foncteur Q de P est tel que Q(c)P(c) et que Q(f) est une restriction de P(f). [l]

Propriété qui nous sera utile : l’ensemble partiellement ordonné (EPO) des sous-objets de tout Foncteur F de la catégorie fonctorielle Ĉ=EnsC^op, ensemble noté SubĈ(P), est une algèbre de Heyting. [m]

VII.6.a Sous-morceau

Qu’est-ce qu’un sous-objet du morceau M ? C’est tout simplement un quodlibet ordonné extrait de M, c’est-à-dire une série d’exemples extraits de M et restant ordonnés selon l’ordre chronologique fixé par τ.

Remarque

On pourrait penser que m serait plutôt une famille particulière d’interprétations de M(Q) : par exemple, si l’on part d’une invention à deux voix de Bach, la famille des interprétations qui privilégient le staccato sur le legato, ou la famille de celles qui « romantisent » le morceau par un phrasé exagérément rubato. Mais dans ce cas, une telle famille ne constituerait plus a priori un faisceau et ne formerait donc plus un morceau-objet de notre monde.

Pour préserver le fait qu’un sous-objet doit toujours être un objet, donc ici un faisceau, il nous faut poser plutôt m(p)↣M(P) avec p⊆P : le sous-morceau de musique n’est pas un sous-ensemble des interprétations du morceau M de départ mais l’ensemble des interprétations d’un sous-morceau q de la partition Q. On écrira :

M’(P’)↪M(P) ⇔ P’⊂P

VII.7 Foncteur représentable

C’est un cas particulier des Foncteurs de Ⓜ dans Ens. [n]

Une topologie pour laquelle chaque foncteur représentable est un faisceau est appelé standard. [o]

VII.7.a Rappel

Cf. à tout M de Ⓜ on associera deux foncteurs Ⓜ[M,-]_covariant et Ⓜ[-,M]_{contravariant} de Ⓜ dans Ens que je note plus simplement ℳ_- et ℳ^-:Ⓜ→Ens

Par exemple, pour le premier ℳ_-=Ⓜ[M,-]

· ℳ_-(M’)={M→M’} : un objet M’ donne un ensemble de morphismes ;

· ℳ_-(f:M’→M”)=ℳ_-(M’)→ℳ_-(M”)={(u:M→M’)→(g:M→M”)} avec g=f°u (un morphisme entre objets donne un ensemble de morphismes entre deux ensembles de morphismes).

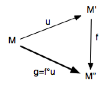
On dit que M représente ces deux foncteurs.

Inversement, un foncteur F : Ⓜ→Ens (co/contra-variant) sera dit représentable s’il existe M tel que F soit naturellement équivalent à Ⓜ[M,-] ou Ⓜ[-,M].

VII.7.b Transposition musicale

Ceci se transpose immédiatement à notre monde : un foncteur représentable de ce monde musical des morceaux vers le monde des ensembles est un foncteur « représenté » par un morceau de musique donné. Ceci désigne en quelque sorte une « représentation » du monde de la musique du point spécifique d’un morceau donné : par exemple le monde de la musique tel qu’éclairé par l’Art de la fugue ou Farben…

VII.8 Catégorie de faisceaux

On a ainsi décrit la catégorie de nos faisceaux qui se trouve ce faisant être dotée des principales propriétés aptes à la constituer en topos.

Mais rappelons-le : cette catégorie, fondée sur les morphismes entre faisceaux que constituent les transformations naturelles entre foncteurs, n’a plus notre monde-Musique pour modèle puisque nos relations musicales entre morceaux de musique (les « influences » musicales) ne sauraient s’ajuster à l’axiomatique catégorielle des morphismes.

VII.9 Passage de la catégorie au topos

Une catégorie de faisceaux (soit un type tout à fait particulier de catégorie), par définition, est un topos de Grothendieck, lequel s’avère (cf. théorème de Giraud) un topos élémentaire (au sens cette fois de Lawvere).

On sait [p] en effet que la théorie des topos résulte de la confluence de deux problématiques : d’abord celle de Grothendieck (topos de faisceaux) [46], et celle – plus logique - de Lawvere (topos élémentaire), le théorème de Giraud venant relier les deux.

Quelles sont les propriétés d’un tel topos qui sont susceptibles de nous intéresser ?

Essentiellement celles qui tiennent à ces objets spécifiques qui délimitent le topos (un topos est une catégorie suffisamment grande et complète pour inclure en son sein une grande variété d’objets).

VII.10 Le classifieur de sous-objets Ω

Pour faire accéder Ω au statut de morceau de musique – le classifieur de sous-objets Ω est un objet particulier du topos -, on imaginera un morceau Ω de notre monde de la musique dont la partition sera le recueil des signes de l’écriture musicale, une sorte donc de manuel de solfège qui détaille, sous forme d’exercices, l’ensemble des symboles musicaux en usage.

On l’appellera morceau-Solfège et on l’écrira M_Ω (pour nous conformer à la notation mathématique du classifieur de sous-objets) en rappelant qu’une fois de plus, M_Ω désigne une classe d’équivalence d’objets « à un isomorphisme près ».

M_Ω=Solfège

VII.11 Les morceaux-limites

L’idée est la suivante : certains morceaux sont fondés sur des partitions si compliquées qu’il convient d’évaluer les différentes interprétations qui en sont proposées non plus deux par deux comme précédemment mais une par une du point de vue cette fois de leur pure et simple qualité d’exécution.

VII.11.a Brian Ferneyhough

Prenons par exemple le cas de cette page d’une œuvre pour guitare solo de Brian Ferneyhough : Kurze Schatten II (1983-1989)

Exécuter cette page de manière exacte ou juste s’avère absolument impossible pour un humain (l’œuvre comporte 24 pages de cet acabit et dure globalement 14 minutes).

Examinons par exemple la dernière mesure de cette page 6 d’un simple point de vue rythmique. La mesure délimite 33 quadruples croches (dans un tempo où la croche vaut 36 et donc la quadruple 288). La mesure au total vaut donc une blanche + une quadruple. Il y faut simultanément :

· partager les 4 premières croches en 7 (7:4) [47] en sorte de n’en jouer que la 6°…

· partager la mesure (de 33 quadruples) en 4 en sorte d’attaquer la 2°…

· partager la mesure en 5 valeurs en sorte d’en attaquer la 3°…

· se livrer à des calculs supplémentaires encore plus détaillés si l’on veut respecter les silences écrits…

L’entreprise est humainement impossible. [48]

Ceci suggère que les interprétations d’une telle pièce vont devenir ordonnables selon le degré d’exactitude ou de justesse de leur exécution.

Entreprenons de formaliser cet ordre.

VII.11.b Fonction Justesse

On posera une fonction J (de justesse ou d’exactitude) de l’interprétation I qui mesure à quel degré d’exactitude l’exécution de la partition est respectée. Cette fonction J(I) opère dans notre intervalle canonique [0,1] qu’on pourra interpréter selon une logique de pourcentage : on dira que J(I)=0,8 veut dire que l’interprétation I exécute la partition à 80% près.

Méthode : une exécution de référence I_midi

On pourra supposer pour ce faire qu’il est possible d’établir pour toute partition une exécution de référence obtenue mécaniquement par un dispositif de type midi. Appelons I_midi cette exécution de référence. On comparera alors, pour tout τ, les résultats de l’interprétation I à ceux de I_midi et on obtiendra ainsi un taux d’exactitude ou de justesse J_τ(I) qu’il suffira ensuite d’intégrer sur l’intervalle [0,1] pour obtenir une valeur globale de justesse de I :

J(I)=J_τ(I)dτ.

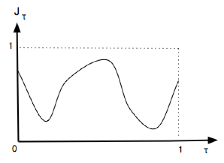
On disposera ainsi d’une évaluation précise de l’interprétation I du point (musicalement très limité) de l’exactitude de son exécution.

Ceci ouvre alors à une mise en ordre de toutes les interprétations-exécutions concevables de cette partition puisque, dans ce cas précis, il est impossible d’obtenir une interprétation vérifiant J(I)=1 c’est-à-dire exécutant à 100% l’ensemble des prescriptions de la partition.

On voit pourquoi cette fonction J acquiert dans ce cas une pertinence musicale quand elle n’en aurait aucune dans le cas d’une invention à deux voix de Bach où l’exécution à 100% peut être très facilement atteinte en sorte que la variabilité musicalement significative des interprétations se situe au-delà de cette justesse ou exactitude parfaite et non pas, comme chez Ferneyhough, en deçà.

Cette remarque indique au demeurant combien une telle « complexité » n’opère pas, comme on le dit souvent, comme un facteur d’ouverture pour les interprètes mais enferme plutôt leur interprétation dans le champ linéairement ordonné des exécutions tentant, a minima, de restituer le texte de la partition dans l’espace propre des sons.

VII.11.c Une structure propre

Ce qui nous intéresse dans cet exemple extrême est qu’il configure ce qu’on appellera un objet-limite de notre monde, un morceau-limite.

On pourrait dire : aucune des exécutions de l’opus de Ferneyhough n’atteignant le seuil d’exactitude adopté partout ailleurs (disons le taux de fausses notes) ne devrait être musicalement admise dans notre monde. Le point est précisément que ces interprétations y sont bien admises et ce pour des raisons proprement musicales qu’il n’y a pas lieu, ici, de détailler.

Ces opus se voient ainsi occuper des positions limites dans notre monde, positions limites qui, au demeurant, suggèrent que ces opus, loin d’ouvrir une nouvelle orientation d’écriture et une nouvelle ressource de musicalisation du sonore (comme peuvent le faire par exemple les opus d’un Helmut Lachenmann auxquels on les compare souvent, à tort me semble-t-il), ferment le monde en en fixant précisément un point-limite, indépassable, du moins dans le cadre d’une écriture musicale. Aller au-delà, si ce n’est pas une absurdité pure et simple, installerait de facto le musicien hors du monde-Musique : dans le pur sonore géré par une écriture non musicale (tel le codage informatique).

Peut-on formaliser ce statut de morceau-limite dans notre topos ?

Esquissons une problématique.

VII.11.d Limites…

L’hypothèse est celle-ci : nos morceaux-limites sont dotés d’une structuration interne spécifique (par la fonction J) et cette structuration propre peut servir de base à un type particulier de morphismes entre ces morceaux-limites et l’ensemble des morceaux « ordinaires »…

Formalisons cela un peu plus avant.

Distinguons les morceaux ordinaires (M) des morceaux-limites (ML).

Le morceau-limite est doté d’une fonction unaire sur les interprétations : J(I)∈[0,1] qui donne naissance à une fonction à deux places : J(I|I’)=min{J(I),J(I’)}∈[0,1]. Les deux fonctions associent à chaque interprétation un nombre unique de l’intervalle [0,1] – un élément et non plus une partie du segment – qui mesure (en pourcentage) la justesse-exactitude de l’interprétation.

Que voit-on si on applique J aux morceaux ordinaires ?

1. On aura d’abord :

∀M≠ML et ∀I(M) : J(I)≃1

Toute interprétation I musicalement validée d’un morceau ordinaire M assure (doit assurer !) le texte de la partition et n’avoir qu’un tout petit nombre éventuel de « fausses notes ».

2. On aura en conséquence :

∀M≠ML et ∀I(M) et I’(M) : J(I|I’)≃1

Deux interprétations I et I’ musicalement validées d’un même morceau ordinaire M seront, du point de vue de leur justesse, toujours équivalentes à 100%.

Où l’on voit que notre fonction justesse, cardinale pour les morceaux-limites, tend à rendre équivalentes toutes les interprétations des morceaux ordinaires : on ne saurait donc plus ordonner deux par deux les interprétations des morceaux ordinaires à mesure du fait que toutes doivent, par définition, être exactes ou justes pour être musicalement valides.

On dira : une interprétation d’un morceau ordinaire doit assurer au préalable qu’elle est une exécution juste. J(I)=1 est une condition nécessaire.

Le morceau-limite, centrant sa mesure propre sur la justesse, est donc ce qui mesure la dimension de pure exécution de l’interprétation I, dimension en-deça de la quelle on ne saurait aller. C’est bien en ce sens que le morceau-limite est une limite : au-delà de lui, l’objet n’est plus musical et redevient un objet sonore, non arrimé à une écriture-partition musicalement évaluable ; au-delà du morceau-limite, l’objet est démusicalisé. Au-delà de lui, la dimension exécution de toute interprétations n’est plus assurée.

La fonction J que génère le morceau-limite peut être alors vue comme un opérateur de mise-en-un de toutes les interprétations I(P) d’une même partition P puisque ∀I(P) et I’(P) : I≡_JI’ (I et I’ s’équivalent du point de leur justesse vis-à-vis de la partition P).

Diagramme : colimite

En vérité, ce morceau-limite relève de ce que la théorie des catégories appelle plus précisément une co-limite. On peut en effet diagrammatiser son opération ainsi :

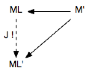
Pour tout morphisme M’→ML et pour tout autre moment-limite ML’, on aura une flèche unique J :ML→ML’ telle que le diagramme commute, ce qui formalise que ML est en position de colimite.

VII.11.e Morton Feldman

La position duale de cette colimite (Ferneyhough) pourra être assignée à ce type de morceaux de musique que Morton Feldman a emblématisé : des morceaux qu’on dira cette fois minimaux dans la mesure où leur écriture est minimale, par exemple ce morceau dépourvu de toute durée (et de toute intensité) :

Au total, on posera donc l’existence de morceaux minimaux (Feldman) ou limites projectives – en deçà, on n’a plus d’écriture musicale - et de morceaux maximaux (Ferneyhough) ou colimites injectives – au-delà, l’écriture n’est plus musicale et bascule dans un autre type d’écriture (informatique, par exemple, ou numérique : codage sonore des sons…) -.

VIII. Notre monde-Musique à l’ombre de la logique philosophique

Il s’agit maintenant d’examiner notre monde de la musique à l’ombre des concepts philosophiques de Logiques des mondes. Qu’en est-il des propriétés phénoméno-logiques de notre monde des morceaux de musique ?

VIII.1Préalables

VIII.1.a Attention au vocabulaire

Faisons d’abord bien attention à un problème de vocabulaire : le même mot n’a pas, dans ce livre de philosophie, exactement le même sens qu’il a dans la mathématique des topos. Ainsi site, objet, point, logique, existence sont des vocables qu’on trouve dans les deux univers avec des sens certes apparentés mais non strictement homologues.

Dans cette partie, on va privilégier leur sens badiousien (en rappelant, quand cela apparaîtra nécessaire, leur équivalent mathématique).

VIII.1.b Attention au philosophème

Il ne va plus s’agir ici de « transposer » les concepts philosophiques de Logiques des mondes dans notre modèle musical comme nous avons tenté de le faire pour les concepts mathématiques de la théorie des topos de faisceaux.

Le rapport musique-philosophie est de nature entièrement différente du rapport musique-mathématiques – je ne vais pas ici m’étendre sur ce point -. Je dirai simplement qu’il va s’agir ici de mettre nos catégories musicales, en particulier celles que nous venons de dégager, à l’épreuve de ces concepts philosophiques (cette philosophie de Badiou étant ici sélectionnée pour des raisons générales sur lesquelles je ne m’étendrai pas plus [49]).

VIII.2Objet/sujet

L’objet du monde de la musique, l’objet proprement musical, c’est le morceau (l’enregistrement n’est qu’un objet sonore). L’objet musical n’est donc pas ici un accord, une mélodie, une cellule rythmique, une tonalité, une série, etc. mais un morceau de musique (une pièce répertoriée de la bibliothèque ou un quodlibet bâti sur cette même bibliothèque).

Le sujet du monde de la musique, c’est l’œuvre musicale (pas le musicien !).

On a ici caractérisé notre monde de la musique sans avoir pour cela besoin de caractériser ce qu’est une œuvre donc un sujet. Nos objets (nos morceaux) n’ont donc nul rapport essentiel à quelque sujet que ce soit (si l’on admet, bien sûr, qu’en musique le sujet n’est pas le musicien mais l’œuvre…).

Le couple objet/sujet est donc bien défait dans notre monde de la musique.

VIII.3Objet

Dans Logiques des mondes l’objet est repensé tout autant que le sujet l’était dans L’être et l’événement. De même que le sujet n’est plus l’individu ou l’être humain, de même l’objet n’est plus dans ce livre un outil qu’on manipule en extériorité mais un site [50] possible pour que quelque chose y advienne.

Ceci se projette dans notre monde de la musique en ce que le morceau de musique va être soumis à la question : pièce ou œuvre ? Le morceau musical va ainsi apparaître comme le site possible pour une œuvre, non pas que le sujet musical soit celui qui instrumente une pièce de musique ou s’en sert (ce serait revenir par la bande à un sujet musicien), mais plutôt que le sujet musical se matérialise en un type tout nouveau de morceau de musique – le lieu n’est pas ici de déployer ce point [51] -.

VIII.4Être & apparaître

On pourrait dire que la partition fixe l’être du morceau de musique et que les interprétations en déploient l’apparaître.

On pourrait donc examiner les rapports interprétations/écriture (ou perception/écriture) à la lumière des rapports apparaîtres/être.

Je ne m’y livrerai pas : l’analogie me semble prêter à confusion, nous engageant sur la voie musicalement périlleuse du philosophème.

VIII.5Transcendantal (classifieur de sous-objets)

Le transcendantal Ω de notre monde (ou classifieur de sous-objets) se présente formellement comme l’ensemble [0,1] en tant qu’il prend mesure de toute partition P (qui se trouve au principe du morceau M) et plus concrètement comme « morceau-étalon » M_Ω.

Ceci pointe en vérité que le transcendantal du monde de la musique met directement en jeu le rapport de la réalité sonore à l’écriture proprement musicale, autant dire au solfège. Le solfège est ainsi constituant du transcendantal du monde-Musique au sens où il est ce qui autorise de prendre musicalement mesure de ce qu’exister veut musicalement dire.

VIII.6Matérialisme du silence musical

Le silence peut être vu comme condensant ce qui en musique fait matière. Il s’agit alors du silence posé comme atome, c’est-à-dire comme couplage d’une marque d’écriture et d’une univocité d’interprétation. Le silence devient ainsi l’univocité du rapport entre deux « uns » :

· l’un d’une marque,

· l’un d’une interprétation.

C’est aussi à ce titre que le silence écrit est au principe du morceau terminal ① et des singletons-atômes musicaux.

VIII.7Conjonction et enveloppe

L’écriture musicale travaille sur une double relation d’ordre : horizontale par les durées, verticale par les hauteurs.

Chacune de ces deux relations d’ordre va donner lieu à conjonction et enveloppe.

Rappelons : les conjonctions sont les maxima des inférieurs, et les enveloppes sont les minima des supérieurs (respectivement les pgi et pps de toute algèbre de Heyting complète).

On aura alors :

	Conjonction ∩	Enveloppe ∪
Durées	Rythmesconj	Rythmesenv
Hauteurs	Fondamentales	Spectres

VIII.7.a Les rythmes

· Les rythmes de conjonction maximisent les durées en commun.

· Les rythmes d’enveloppe minimisent les durées résultantes.

Soit, avec deux rythmes A et B donnés :

VIII.7.b Du côté des hauteurs

· Les fondamentales maximisent les harmoniques générateurs.

· Les spectres minimisent les harmoniques résultants.

VIII.7.c Au total

VIII.8Dépendance et envers

VIII.8.a Envers

Rappel

C’est la complémentation au sens de l’algèbre de Heyting (ou pseudo-complémentation absolue) : ∼a est le plus grand ouvert ne contenant pas a qu’on note parfois [q] (non-a)°. C’est l’intérieur du complémentaire ensembliste de a.

Comme l’on sait, cet envers est une négation particulière puisque, en général, ∼∼a≠a (a⊆∼∼a) : cette double négation « agrandit » topologiquement l’objet initial en lui ajoutant son adhérence.

La particularité de cette négation tient au fait de travailler ici sur les seuls ensembles qui, dans une topologie donnée, sont des ouverts.

Musicalement ?

En première approche, on considèrera que cette nuance n’est pas d’une importance capitale pour notre compréhension des morceaux et du monde-Musique.

Ceci, somme toute, tient au point suivant : en musique, la négation (qu’elle soit ensembliste – complémentarité – ou topologique – envers -) n’est pas un opérateur évident. Le développement musical travaille plutôt par contrastes (a⋂b=Ø) et altérations (a⋂a’=a”) que par négation proprement dite.

D’où l’intérêt par contre de la notion suivante de dépendance ou pseudo-complémentation relative à un objet donné (et non plus absolue pour a dans un ensemble-tout donné).

VIII.8.b Dépendance

Le concept de dépendance (de l’objet b vis-à-vis de l’objet a : a⇒b) dans Logiques des mondes correspond à la notion de pseudo-complémentation d’un objet relativement à un autre. [52]

Dans la logique des propositions a⇒b désigne « non a ou b ». [r]

Rappel

La pseudo-complémentation de a relative à b (dans l’ensemble E) désigne la plus grande partie c de E telle que a⋂c⊆b.

On a c=∼a∪b

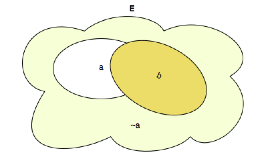
Où l’on voit par exemple que

— si a⊂b, alors (a⇒b)=E : la dépendance de b par rapport à a est partout assurée.

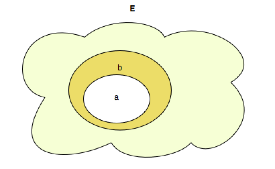
— bien sûr (cas particulier : a⊆a) : (a⇒a)=E

— si a⋂b=Ø, alors (a⇒b)=∼a (la pseudo-complémentarité relative se rabat alors sur le simple envers de a) : si a et b sont disjoints, la dépendance de b relativement à a recouvre exactement l’extérieur de a.

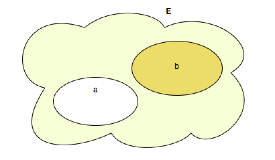
Rappelons : une algèbre de Heyting est un treillis (ensemble partiellement ordonné) doté d’une telle pseudo-complémentarité relative et d’un minimum.

Philosophiquement…

Dans Logiques des mondes [s], un tel type de pseudo-complémentation relative, renommée « dépendance », va jouer entre les degrés du transcendantal (T=Ω) d’un monde.

Musicalement ? Un développement qui soit une variation-altération plutôt qu’une déduction

La difficulté ici de « transposer » - cette fois de la philosophie vers la musique – tient au léger décalage entre notre formalisation et celle que Logiques des mondes met en œuvre pour son compte propre. Il va de soi que nos objectifs (pratique théorique de musicien) assument un tel léger décalage par rapport aux objectifs proprement philosophiques de Badiou (fonder une Grande Logique philosophique, renouant dans les conditions d’aujourd’hui, avec l’ambition de Hegel et débordant de toute part la petite logique langagière qui encombre le paysage depuis le supposé « tournant linguistique »).

Si la notion de « dépendance » est susceptible d’une certaine pertinence dans ce travail musicien, ce sera donc de manière légèrement décalée.

Je me contenterai ici d’avancer une hypothèse : la catégorie de dépendance relative d’un objet B par rapport à un objet A peut nous mettre sur la piste d’une compréhension non implicative du développement musical. Précisons rapidement.

Pierre Boulez – dont on sait combien l’orientation constructiviste de sa pensée est étroitement associée à une thématisation du discours musical comme langage [53] - exhausse régulièrement la dimension déductive du développement musical : pour lui un compositeur est un musicien qui sait déduire des conséquences musicales de son matériau.

Le point – on l’a déjà relevé – est que si on note « ⇒ » une telle déduction (par exemple T⇒T’ désignera que l’objet-thème T’ est déduit de l’objet-thème T), une telle opération n’apparaît comme telle nulle part lors d’un morceau de musique : ni dans la partition, ni dans l’exécution sonore. La seule opération phénoménale qui intervient musicalement est celle de consécution. Mais l’on sait parfaitement en musique que ce n’est pas parce que B suit A que pour autant A engendre B – c’est même très exactement le reproche que Boulez fait aux mauvais compositeurs : ils écrivent des successions qui ne sont pas des déductions -.

Pour ma part, j’ai toujours été très sceptique sur cette catégorie de déduction (qui, en deux mots, me semble relever unilatéralement d’un style constructiviste de pensée musicale) et j’ai plutôt cherché du côté de « développements » musicaux qui ne soient pas déductifs (sans pour autant être bien sûr de purs collages éclectiques). D’où l’idée de concevoir le développement musical comme une variation-altération (Veränderung).

L’idée de « dépendance », formalisée avec un signe « ⇒ » (A⇒B) qui désigne cette fois non plus l’engendrement de B par A mais un nouveau site (∼A∪B) ajusté au degré d’altération que B comporte vis-à-vis de A, peut à ce titre s’avérer stimulante.

L’idée, très simple, serait alors la suivante : B ajouté à A disjoint, dans la situation musicale de départ, deux nouvelles parties : d’un côté A rogné de B, de l’autre le reste.

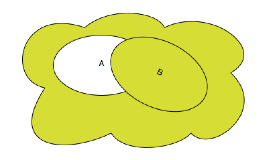
D’où une série de variations-altérations qui vont successivement « éclairer » ce qui de l’objet A de départ (mettons le thème initial de notre situation E) résiste :

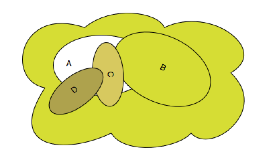
Bref, il y a, en ce concept de « dépendance », matière sans doute à formaliser ce qu’il en est d’un développement musical qui enchaîne par succession sans à proprement parler déduire.

VIII.9Foncteur transcendantal

VIII.9.a Rappel

Badiou désigne ainsi le couple (A, Id) qui associe à tout degré i de Id la partie de l’objet-site A telle que Id(A)=i – qui « découpe » l’objet-site A selon les degrés d’intensité dans l’apparaître -.

Cela pourrait désigner pour nous l’analyse musicale des différentes interprétations d’un même morceau selon le couple (M,J) - plutôt que (M,R) - en sorte de les classer selon le degré d’exactitude de leur exécution. Mais ce n’est pas musicalement très éclairant.

VIII.9.b Problème

On pourrait transposer cela un peu autrement : cette fois comme découpage d’une interprétation donnée selon les moments où son exécution est plus ou moins fidèle (on l’a vu : c’est là l’objet même de la fonction Justesse J).

La difficulté est patente : en ce point, la transposition de l’idée philosophique ne marche guère car notre fonction J – on l’a vu – n’est musicalement pertinente que pour les morceaux-limites alors qu’elle reste muette pour les autres types de morceau (où la condition J≅1 est un préalable - pour admettre musicalement l’exécution – et non pas une cible inatteignable).

Laissons ici cette difficulté non résolue…

VIII.10 Points du topos

Cela peut s’entendre comme les moments névralgiques des différents morceaux de musique, en particulier comme index de possibles moments-faveurs autour desquels l’écoute musicale peut se constituer comme telle et donc une œuvre musicale se constituer en surplomb de la simple audition d’une pièce de musique.

On remarquera que la conjonction matérialiste point/atôme de Logiques des mondes a pour exacte contrepartie (transposition) dans notre monde-Musique la conjonction moment-faveur/silence, ce qui pointe cette donnée musicalement capitale : un moment-faveur est toujours, peu ou prou, un moment de vertige généré dans un discours musical par un silence-vide imprévu…

IX. Un monde-Musique

IX.1 Récapitulation

Récapitulons ce que notre pratique théorique de formalisation a dégagé.

1. Un morceau de musique (pièce ou œuvre) est le faisceau des interprétations (ou exécutions) d’une partition donnée.

2. Les objets du monde-Musique sont des morceaux musicaux. Ce ne sont donc nullement les musiciens.

3. Un morceau admet des sous-morceaux formés à partir de quodlibets extraits de sa partition.

4. Le monde-Musique est l’ensemble des morceaux que supporte une bibliothèque ordonnée (classée) de toutes les partitions (transcriptions comprises qui transforment certains objets sonores en objets musicaux) ; ces morceaux incluent l’ensemble des quodlibets concevables à partir des pièces répertoriées dans la bibliothèque.

5. Les silences écrits (un silence sonore n’est musical que s’il est écrit) constituent les atômes insécables de nos morceaux.

6. Le monde-Musique a un morceau initial (Stockhausen) et un morceau terminal (Cage). Il comporte également des morceaux minimaux-limites (Feldman) et maximaux-colimites (Ferneyhough) en-deça ou au-delà desquels on sortirait de ce monde (par défaut ou excès d’écriture musicale)…

7. Les différentes composantes d’un morceau musical (c’est-à-dire ses différentes exécutions-interprétations) sont ordonnables deux par deux selon une fonction de ressemblance indexée sur la partition selon Ω=[0,1]. Un morceau-Solfège vient donner figure d’objet à cet Ω qui sert de référence pour toute mesure de la composante exécution de toute interprétation.

8. Les deux opérateurs fondamentaux de synthèse musicale sont le rythme (de conjonction ou d’enveloppe) et le timbre (conjonction par les fondamentales et enveloppe par les spectres).

9. Le monde-Musique ainsi conçu est structuré de part en part par le solfège.

10. Les points du monde-Musique (où celui-ci éprouve donc son réel propre) mobilisent le silence écrit comme atome de ce que la musicalisation du sonore signifie.

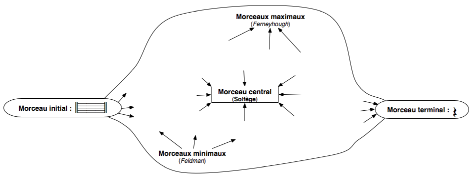
IX.2 « Monde » ?

Reformulons ce que veut dire, pour nous musiciens, que la musique forme un monde, un tel monde-Musique.

· Cela veut essentiellement dire que la musique est dotée d’une consistance autonome de monde par une logique qui lui est propre et qui s’arrime dans son écriture propre : dans son solfège. L’autonomie de la musique comme monde est gagée sur son solfège (invention, comme l’on sait, précisément datable et qui traverse ensuite des péripéties interminables). Travailler au développement du « solfège » en sorte de doter la musique de nouvelles possibilités de « musicaliser » le sonore est une tâche musicalement stratégique.

· De ce point de vue, l’attention à ce qui rend un silence spécifiquement musical (et qui repose sur une marque d’écriture propre) est capitale : un silence musical tend à être doté de propriétés stratégiques et pas uniquement tactiques.

· La musique est un monde de morceaux, non de musiciens. Le musicien connaît et pratique ce monde-Musique mais il n’en est pas un « objet » : le musicien n’est pas un habitant du monde-Musique mais un visiteur.

Le musicien n’est pas plus le sujet de ce monde-Musique s’il est vrai qu’il nous faut chercher des sujets proprement musicaux du côté des œuvres musicales (entendues comme type tout à fait spécifique de morceau : essentiellement celui qui ordonne son cours à la constitution d’une écoute musicale et non pas à une simple perception sonore ou à une pure audition).

La question du musicien reste donc entière une fois dégagée l’existence spécifique du monde-Musique.

· De même pour la question spécifique de l’œuvre musicale : le monde-Musique n’est pas fait d’œuvres mais de simples pièces. Et il ne va nullement de soi qu’un tel monde-Musique supporte cette forme tout à fait singulière d’existence musicale qu’est l’œuvre.

· Le monde-Musique est clos sur lui-même, en particulier par des morceaux-limites et co-limites qui en fixent les bornes (quand un morceau initial et un morceau terminal en fixent les extrémités) : au-delà, tout morceau bascule dans le pur et simple sonore, devient « démusicalisé ».

· Le monde-Musique est un chatoiement infini des rapports entre ses morceaux, comme l’exemple le plus simple (celui des quodlibets avec ses rapports d’inclusion) le montre bien. Le fait que notre formalisation attrape mal ces rapports ne doit pas laisser penser qu’ils seraient sans importance musicale et que notre monde-Musique pourrait être vu comme pur et simple amas chaotique de morceaux. La vie musicale effective des morceaux repose certes sur les exécutions incessamment renouvelées de leur partition mais, ce faisant, elle met en jeu un ensemble de relations, rapports, interactions entre ces morceaux (l’idée de quodlibets extraits non plus d’une seule partition mais bien de la totalité de la bibliothèque en donne une petite image) qui composent la vie même de ce monde. Que ces relations musicales (par exemple celle qu’un concert donné établit entre les exécutions successives de différentes partitions) soient plus difficilement formalisables dans le cadre de la théorie des topos que ne le sont les morceaux ne doit pas nous faire oublier qu’elles sont musicalement essentielles : la pensée du musicien ne doit nullement se cantonner à cette pratique théorique (son idéation ne s’y limite nullement), et ses idées propres de musicien ne se réduisent nullement aux idées mathématiquement formalisables.

· Au total, on peut sur cette base envisager (ce sera un autre travail) d’exposer plus systématiquement comment ce monde fait d’objets et de leurs relations – sa structure donc -, et de quoi il s’avère capable…

IX.3 L’objectivation procède d’un monde-Musique qui constituant

On pourrait croire, à suivre notre mouvement d’exposition, qu’on fait un monde à partir d’objets : par assemblage d’objets, et qu’on ferait donc le monde-Musique à partir de morceaux (de musique). Mais c’est en vérité tout l’inverse : c’est le monde qui fait l’objet, et c’est le monde – non le sujet [54] – qui est l’objectivation, ce qui se dit ici : c’est la musique qui fait le morceau de musique.

On discerne clairement ce point dans le rôle central ici joué par l’existence d’une partition, donc du solfège musical : sans partition, sans solfège, sans écriture musicale, pas de morceau de musique ; sans tout cela, la musique ne fait pas monde. Ce qui découpe un morceau dans la musique, c’est la partition, c’est elle qui délimite l’un musical du morceau.

Sans écriture musicale, pas de monde-Musique. Sans solfège, il y a certes « de la musique », mais cette musique ne fait pas monde et donc n’objective pas, est dans l’incapacité d’objectiver (au sens donné ici, à l’ombre de la philosophie de Logiques des mondes, à la catégorie d’objet) – voir sur ce point l’exemple de l’antique musique grecque -. Sans son écriture la musique ne saurait découper ses objets. Sans solfège, il y a sans doute des objets sonores, mais la musique n’est pas en état de constituer ses propres objets musicaux (c’est, au demeurant, une grande leçon - par la négative peut-on dire – du Traité des objets musicaux de Pierre Schaeffer puisque son échec avoué est de n’avoir pas pu déduire les objets musicaux des objets sonores, faute précisément d’un solfège adéquat).

Il ne faut donc pas confondre notre mouvement d’exposition, qui suit l’élaboration théorique des topos de faisceaux en entreprenant de lui donner pour modèle un monde-Musique de morceaux musicaux, avec un mouvement qui serait constituant : si notre pratique théorique opère des faisceaux-morceaux aux topos-monde, cette démarche, qui peut être mathématiquement constituante, en tous les cas ne saurait l’être musicalement.

Ceci se voit d’ailleurs immédiatement dans le fait suivant : il nous a bien fallu supposer, au principe même de ce travail, l’existence de musiciens, de partitions, de morceaux de musique, et finalement d’un monde-Musique pour arriver à constituer les bases de notre modèle, en particulier pour considérer qu’il existe bien « quelque part » - mais ce « quelque part » est précisément le monde-Musique – de quoi se prononcer sur la validité proprement musicale de telle ou telle exécution de telle ou telle partition. On a donc bien supposé qu’il existait musicalement un tel monde-Musique pour pouvoir alors entamer la tâche musicienne de le formaliser. Et ce n’est bien sûr pas cette pratique théorique qui porte à l’existence un tel monde : elle se contente de dégager théoriquement sa structure toposique.

X. Annexe : Discrétisation de la fonction interprétation I

Que fait un logiciel de partition tel Finale ? Il transforme les lettres du solfège en données numériques « midi » susceptibles d’être alors mécaniquement exécutées en sorte de générer une image sonore exacte de la partition. Le principe de cette « midification » repose sur l’idée de ce que le logiciel Max appelle une « Q-list » c’est-à-dire une liste d’instructions ordonnée et quantifiée. Le principe revient à construire un fibration temporelle : on strie (verticalement) l’intervalle [0,1] de la partition en sorte d’identifier, par une série τ_i, les instants où il se passe quelque chose (une hauteur est attaquée, ou est arrêtée…) et d’associer à chacun de ces τ_i une liste (verticale) d’actions ou d’événements (attaquer telle hauteur, arrêter telle autre…). [55]

Notre fibré se trouve alors constitué

· d’une base temporelle : notre série de τ_i convertie en une série de t_i (« temps réel ») selon les caractérisations fournies par les tempi et plus généralement l’agogique notées dans la partition ;

· d’une série de fibres qui vont prendre la forme d’un vecteur vertical composé des 128 intensités données aux 128 hauteurs distinguées dans la formalisation midi [56]. Détaillons cela.

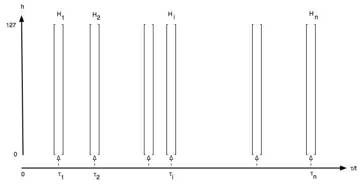
Chaque vecteur Hi est composé de 128 valeurs a_j,i qui vont donner forme de matrice à notre ensemble :

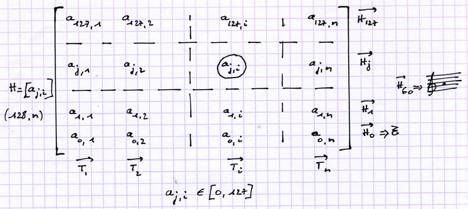
H₀ désignera la hauteur-silence.

La valeur de a_i,j (qui appartient à l’intervalle 0-127) désigne ici l’intensité propre de la hauteur H_j à l’instant T_i de la partition P. Lorsqu’une hauteur doit devenir silencieuse (car sa durée d’exposition s’arrête), cette valeur devient 0 : a_0ij = g

Il faut compléter le dispositif de la donation d’une matrice uni-ligne (ou vecteur) qu’on notera T et qui donne les valeurs cette fois en temps réel t (et non plus en temps proportionnel τ de la partition) des instants constituant la base de notre fibré temporel :

T=[t₁, …, t_i, … t_n]

Au total, notre fonction associe à la partition P l’ensemble d’une matrice uniligne T (1,n) et d’une matrice H (128,n) :

X.1.a Remarque

On pourrait imaginer de calculer Hxtr(T) [T transposé en vecteur uni-colonne] : cela donnerait la matrice uni-colonne des H_j=∑_i h_j,i.t_i qui représenterait en quelque sorte le poids de la hauteur H_j dans l’ensemble du morceau…

X.1.b Foncteur

On a ainsi bâti un foncteur θ(P)→Ens qui associe à tout ouvert de la partition P le couple des matrices <T(1,n), M(128,n>.

On voit clairement que ce foncteur - qu’on désignera ici par la lettre σ (pour indiquer qu’il correspond à une pure et simple opération de solfégiation) – est lui-même un faisceau.

On voit tout de suite que les deux foncteurs I (interprétation : application continue) et σ (solfégiation : application discrète) sont alors reliables par une transformation naturelle qu’on notera ∂ (pour discrétisation) :

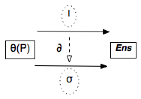
qui va mettre en correspondance les deux applications :

I : θ(P)→<t(τ), {a_τ(f)}>

σ : θ(P)→<T(τ_i), H=[a_j,i]>

À la fonction continue τ→t correspond l’application discrète τ_i→t_i ; à l’autre application continue générant une fonction continue τ→a_τ(f) correspond l’application discrète générant une matrice τ→[a_j,i].

La transformation naturelle « discrétisation » fait alors commuter le diagramme suivant :

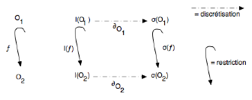
XI. Notes de références bibliographiques

[CWM] : Catégories for the Working Mathematician de Sanders Mac Lane

[SGL] : Sheaves in Geometry and Logic. A First Introduction to Topos Theory de Sanders Mac Lane et Ieke Moerdijk

---

[1] Cf. Des connivences entre intellectualités musicale et mathématique (mamuphi, 9 octobre 2008) :

http://www.entretemps.asso.fr/Nicolas/2008/Connivences.htm

[2] Cf. La troisième audition est la bonne (De l’audition musicale conçue comme une intégration), Musicæ Scientæ (n° 2, 1997) :

http://www.entretemps.asso.fr/Nicolas/TextesNic/Audition3.html

Comment l'écoute tricote du temps (Penser le temps musical avec Lautman), polycopié Ens (19 février 2004) :

http://www.entretemps.asso.fr/Nicolas/Ecoute/6.html

[3] Cf. Le concert/Enjeux, fonctions, modalités, ouvrage collectif dirigé avec F. Escal (L’Harmattan, 2000)

[4] Cf. Peyresq (août 2008) : http://www.entretemps.asso.fr/Grothendieck/Peyresq.htm

[5] Les rapports musique-mathématiques, saisis de l’intérieur de la musique, musicalement donc, et par le musicien pensif, sont certes musiciennement pensables – c’est bien là le défi de ce travail – mais par contre la pensée de cette pensée ne saurait être immanente à la pensée du musicien : en ce point, il faut la philosophie.

En ce point se dessine une ligne de partage, essentielle pour mamuphi, avec le vaste travail de G. Mazzola. Celui-ci accouple en effet sa théorie mathématique de la musique (qui renoue – c’est sa grandeur - avec le projet eulérien) à une musicologie computationnelle et thématise l’ensemble ainsi constitué comme une manière d’adjoindre mathématiques et musique. Cette manière de réfléchir les rapports mathématiques-musique selon des notions intra-mathématiques, l’adjonction en l’occurrence, et non selon des concepts philosophiques (comme si la mathématique pouvait, de l’intérieur d’elle-même, envelopper ses rapports extérieurs - à la musique en l’occurrence -) le conduit à la construction de mythes (son mythe de la vérité mathématique du beau musical, son mythe de voisinages musicaux – celui par exemple de la HammerKlavier et de L’Essence du bleu -), ce qui confirme bien, s’il en était besoin, qu’en cette réflexion des rapports mathématiques-musique, il en va d’une alternative « mythe ou philosophie » (il est bon de rappeler que cette alternative est elle-même constitutive de la philosophie : voir le Poème de Parménide).

Voir également la manière dont Charles Alunni a reconvoqué cette alternative « mythe ou philosophie » en matière de compréhension bachelardienne de ce qu’un « temps long » peut être.

[6] Remarquons, à ce titre, la convergence inattendue entre cette approche et celle que René Guitart prônait dès 2002 (voir sa contribution « Que peut-on écrire et calculer de ce qui s’entend ? » au volume mamuphi « Penser la musique avec les mathématiques ? » - Delatour, 2006), et qui l’amenait à écrire : il conviendrait « de voir une partition comme un site de Grothendieck, […] une interprétation comme un faisceau sur ce site, et l’espace des interprétations comme le topos de ces faisceaux. » (p. 146). Cette proximité incite à pousser plus avant les confrontations musiciens/mathématiciens sur la pertinence musicale du concept de faisceau. Remarquons cependant le décalage entre cette proposition de formalisation (les interprétations d’un même morceau de musique constitueraient un topos) et celle tentée dans ce texte (ces interprétations d’un même morceau constituent un faisceau et c’est seulement l’ensemble des morceaux qui constitue un topos). En vérité ce dilemme de formalisation s’avère, en l’état de cette expérimentation théorique, se situer au cœur même de notre problème.

[7] Écart supplémentaire, concernant cette fois l’ordre d’exposition : là où Logiques des mondes privilégie l’approche logique des topos (topos élémentaires de Lawvere) pour des raisons immédiatement liées à son propos philosophique (reconstituer l’espace d’une Grande logique proprement philosophique), mon approche abordera les topos par leur versant ontologico-mathématique (topos de faisceaux de Grothendieck) - au demeurant le premier à s’être chronologiquement constitué - puisqu’elle fait l’hypothèse que « l’être-là » d’un morceau de musique (dans le monde de la musique) est formalisable comme faisceau.

On circule ici des faisceaux vers les topos (des morceaux vers le monde-Musique) quand Logiques des mondes circule pour sa part du monde-topos vers ses objets-faisceaux…

[8] Un faisceau est un ensemble doté d’une structure particulière. S’il va quasi de soi qu’une pièce de musique peut être vue comme « l’ensemble des interprétations de sa partition », il ne va plus de soi que cet ensemble ait particulièrement la structure d’un faisceau.

[9] Même remarque que précédemment : un site est un ensemble doté d’une structure (topologique) particulière. S’il va de soi qu’une bibliothèque est l’ensemble des partitions qu’elle regroupe, il ne va plus de soi que cet ensemble ait particulièrement la structure d’un site.

[10] Même remarque que les deux précédentes : une catégorie est un ensemble d’objets (ici de morceaux) doté d’une structure particulière, en particulier par ses relations (« morphismes ») entre ses objets.

[11] Toujours la même remarque : un topos est un ensemble doté d’une structure catégorielle particulière. S’il va de soi qu’un monde est l’ensemble de ses choses et de leurs rapports, il ne va plus de soi que cet ensemble ait particulièrement la structure d’un topos.

[12] Morceaux = pièces + œuvres

[13] Attention : « modèle » doit s’entendre ici au sens logico-mathématique qu’il a dans « la théorie des modèles » et non pas au sens empirico-positiviste, inverse, qu’il a dans « la modélisation mathématique ». Le modèle est ici l’original à copier (cf. le modèle pour un peintre), non le « modèle réduit », la maquette, donc la copie.

[14] À l’inverse, une catégorie donnée devient un topos par une série de conditions sur ses objets (existence d’objets-limites, etc.) et non plus sur ses morphismes.

[15] Cette conception d’un monde, on l’aura compris, n’est pas une Weltanschauung…

[16] L’axiome inverse (le musicien fait la musique) sera dit axiome nihiliste de Duchamp…

[17] Autrement dit : il en va ici de la possibilité spécifiquement musicale d’une écoute qui ne se réduise ni à une perception psycho-physiologique, ni à une audition savante.

[18] Le sociologue qui « théorise » ce point de vue s’appelle Howard S. Becker. Voir son livre « Les mondes de l’art » (Art Worlds, Flammarion, 1988) et cette définition, évidemment circulaire : « Un monde de l’art se compose de toutes les personnes dont les activités sont nécessaires à la production des œuvres bien particulières que ce monde-là (et d’autres éventuellement) définit comme de l’art. » (p. 58).

[19] en torsion subjective explicite, non en déduction linéaire…

[20] Un topos n’a pas d’autre « matière » que ses objets et leurs morphismes…

[21] Rappelons que ce point distingue radicalement la phénoménologie de Badiou de celle de Husserl (voir par exemple Logiques des mondes p. 185-6)

[22] Philosophiquement dit : l’art musical de l’écoute faisant vérité du monde-Musique, les œuvres produisent les vérités de ce monde.

[23] Ceci règlera par le haut les questions scolastiques traditionnelles en matière de phénoménologie musicale, du type « qu’est-ce qu’un opus musical ? : est-ce sa partition ?, mais alors l’existence musicale serait essentiellement muette… Et si l’opus n’existe musicalement qu’interprété, alors cette existence serait essentiellement volatile (le temps de l’exécution) et plurielle (il y en aurait autant d’existences distinctes qu’il y en a d’interprétations différentes)… » Etc…

[24] On ne distinguera pas ici exécution d’interprétation. En toute rigueur, cette distinction renvoie à celle entre pièces et œuvres de musique, distinction qui n’est pas ici mise en jeu.

[25] Il faudra plus tard se demander si l’intuition philosophisante qu’une interprétation serait l’apparaître (l’être-là) d’une œuvre dont la partition serait « l’être » - la partition comme structuration saisie à partir du vide – est ou non pertinente…

[26] prise de son uniforme, taux d’échantillonnage constant, etc.

[27] taux de résolution constant, etc.

[28] Rappelons : on ne retient ici que les interprétations musicalement valides, pas les prises ratées, interrompues, etc.

[29] On retient comme échelle des amplitudes cet intervalle plutôt que l’intervalle [0,127] de la norme Midi…

[30] expression qui en quelque sorte compactifie S{E[I(P)]}.

[31] Disons « la nature » de leurs effets, au sens où Galilée parlait d’une « nature » [pas d’un sujet !] « écrite en langage mathématique »…

[32] au sens où elle est sans contenu musical propre, sans signification musicienne distincte…

[33] Il va de soi que notre formalisation ne touche qu’à la perception et l’audition musicales, la question spécifique de l’écoute musicale renvoyant à des déterminations proprement subjectives qui ne sauraient être formalisées dans ce cadre mathématique…

[34] Rappelez-vous l’ancienne Tribune des critiques de disques sur France-Musique où André Boucourechliev s’opposait à Antoine Goléa !

[35] Je m’y livre, de préférence, à propos de ce que j’appelle les moments-faveur des œuvres…

[36] J’en sais quelque chose comme compositeur s’il est vrai que je commence toujours une œuvre en m’en donnant d’abord un plan global.

[37] Cf. le « bar » wagnérien : A₁-A₁’-A₂

[38] Voir La troisième audition est la bonne (De l’audition musicale conçue comme une intégration), op. cit.

Je tiens que l’écoute musicale procède d’une tout autre logique : celle de l’œuvre musicale et non plus de la simple pièce de musique…

[39] Solfège désigne ici l’amas désordonné et chaotique de l’écriture musicale proprement dite (« notes ») et des notations hétéroclites qui la complètent (mots, signes, dessins, codes variés, neumes, tablatures…)

[40] La pratique musicale avère que le partage pièce/œuvre est subjectivement décidé plutôt qu’objectivement scellé, qu’il est donc mobile puisqu’il dépend d’un traitement musicien : la partition d’une simple pièce de musique peut, grâce à une interprétation musicale d’un genre tout nouveau, s’avérer constituer la base possible d’une véritable œuvre - songeons par exemple au destin des études pour piano dont on voit bien (cf. Chopin) comment ce genre de « morceau » oscille entre « pièce » et « œuvre » selon l’interprétation musicienne -.

[41] Un topos de Grothendieck est, par définition, une catégorie équivalente à une catégorie de faisceaux sur un site.

[42] Pullback

[43] Pushout

[44] On sait qu’une version de 4’33”, écrite en notation proportionnelle, a été réalisée par l’auteur en 1960. Cette partition doit donc être vue comme une transcription (!!!) par l’auteur du morceau concerné…

[45] Remarquons qu’il n’y aurait pas ici de sens musical à remplacer cette partition vide par une transcription d’une exécution donnée. En effet l’ensemble des exécutions d’une pièce donnée d’ADST (et donc l’ensemble des transcriptions envisageables qui en découle) ne saurait constituer un « faisceau » : il est musicalement impossible de décider si une exécution donnée (et présentée comme exécution d’ADST) relève bien fidèlement d’une telle partition verbale (comme en a récemment attesté les ateliers musicaux organisés au CNR de Paris au printemps 2008 autour du colloque « Mai 68 et la musique »…).

[46] Voir à partir de 1963 SGA IV : 3 volumes de Springer-Verlag pour un total de 1623 pages…

[47] Attention : pour une raison qui ici m’échappe, et comme pour compliquer encore l’écriture (s’il en était besoin…), la partition indique d’une noire entre parenthèses qu’il faut compter les durées comme doubles de leur valeur écrite !

[48] Est-elle pour autant musicalement absurde ? Cela ne va nullement de soi – voir à ce propos mes propres articles sur la musique de Brian Ferneyhough -.

[49] Voir l’exposé mamuphi du 12 mai 2007 : En quoi la philosophie de Logiques des mondes (Alain Badiou) peut servir au musicien (ou la question d’un matérialisme de type nouveau).

Texte http://www.entretemps.asso.fr/Nicolas/2006.2007/sur.LDM.htm

Vidéo Diffusion des savoirs : www.diffusion.ens.fr/index.php?res=conf&idconf=1642

[50] Corrélativement, le concept philosophique de « site » (événementiel) ne recouvre pas la notion grothendieckienne de « site »…

[51] En deux mots, l’œuvre musicale se caractérise d’un projet d’écoute (qui s’écarte de la simple audition des pièces de musique et de leur perception corrélative)…

[52] Lacan, pour sa part, a nommé cette relation celle du « ou aliénant » (27 mai 1964). Son exemple canonique est celui-ci : « La bourse ou la vie ! Si je choisis la bourse, je perds les deux. Si je choisis la vie, j’ai la vie sans la bourse, à savoir, une vie écornée. » (Séminaire XI ; p. 192) Voir aussi « La liberté ou la mort ! »…

[53] Voir

· « L'intellectualité musicale de Boulez » http://www.diffusion.ens.fr/index.php?res=conf&idconf=580 et http://www.entretemps.asso.fr/Nicolas/IM/Colloque.Boulez.htm

· « La catégorie de langage musical chez Boulez » : http://www.entretemps.asso.fr/Nicolas/IM/VIII.Boulez.langage.htm

· « La théorie musicale de Pierre Boulez » : http://www.entretemps.asso.fr/Nicolas/Textes/Boulez.theorie.htm

[54] Je rappelle : ce point distingue la phénoménologie badioussienne de toutes les autres…

[55] On néglige ici le paramètre « timbre »…

[56] On pourrait bien sûr se contenter ici des 88 hauteurs distinguées par le piano, mais les données midi ont pour intérêt propre leur généralité. En particulier elles autorisent facilement la prise en compte des micro-intervalles grâce aux « midi cents » c’est-à-dire tout simplement le passage de ℕ à ℚ.

---

[a] SGL, 65

[b] Géométrie algébrique, Daniel Perrin, CNRS Éditions, p. 45

[c] SGL, 66

[d] Voir SGL, 65

[e] Voir par exemple

— Toposes, Triples and Theories de M. Barr et C. Wells (Springer-Verlag, 1985) : 6.7. - Grothendieck Topologies (p. 232…)

— An introduction to sheaves, de Pierre Schapira (2006) : 2.1 - Grothendieck Topologies (p. 17…)

[f] Cf. Goldblatt p. 374

[g] Cf. Schapira : ex. 2.1.7 (i) p. 19 ; Goldblatt, ex. 1 p. 375

[h] Cf. Laurent Schwartz : Analyse (Hermann, 1970) ; chapitre VIII : Espaces compacts (p. 81)

[i] SGL, 67

[j] SGL, 30

[k] SGL, 39

[l] SGL, 36

[m] SQL, 56

[n] Cf. Lavendhomme p. 305

[o] Cf. Barr & Wells p. 236

[p] Voir par exemple Barr & Wells (87-89)

[q] Goldblatt p. 180

[r] SGL, 51

[s] Goldblatt pp. 144… et 183…