« Un pays où les enfants mènent
boire les chevaux »
(De
la musicalité de Récoltes
et Semailles d’A. Grothendieck)
Peyresq,
27 août 2008
Semaine
Grothendieck 24-30 août 2008 (dir. P. Lochak, W. Scharlau, L. Schneps)
« Ich liebe die, welche nicht zu leben
wissen, es sei denn als Untergehende, denn es sind die Hinübergehenden. » [ J’aime ceux qui ne savent vivre à moins de se perdre, car
ce sont ceux qui passent sur l’autre rive. ]
Nietzsche
(Ainsi parlait Zarathoustra, Prologue 4)
Mon exposé sera celui d’un musicien, qui n’est
ni mathématicien (j’ai appris ce qu’est un mathématicien au contact de Laurent
Schwartz), ni philosophe (j’ai appris ce qu’est un philosophe au contact
d’Alain Badiou).
Un exposé de musicien s’adressant à des
mathématiciens pour leur parler de mathématiques (et non pas de musique) :
le défi est majeur !
J’aurais pu minorer le défi en vous faisant un
exposé sur la musique plutôt que sur les mathématiques. J’aurais pu ainsi vous
exposer :
·
comment la mathématique de Grothendieck
éclaire la musique, par exemple par sa problématique des faisceaux en vue de
caractériser un topos (ceci m’aurait donné l’occasion d’engager une discussion
critique du Topos of music de G. Mazzola [1]),
ou par son art de la conjecture (voir l’exposé d’Yves André [2]
et les interrogations musicales qu’il peut susciter en matière de développement
thématique…) ;
·
comment le mathématicien Alexandre
Grothendieck instruit par ses écrits propres (Récoltes
et Semailles…) le musicien : par exemple sa
manière de distinguer deux manières de résoudre un problème mathématique (par
effraction au moyen d’un burin, ou par dissolution patiente au moyen d’une
immersion) éclaire deux logiques thématiques en musique (par fracturation du
thème en motifs, ou par déploiement de variantes mélismatiques [3]) ;
de même la distinction de ses deux figures de mathématicien (le pionnier et le
bâtisseur) consonne avec la distinction de deux figures de compositeur :
celui qui conquiert de nouveaux territoires sonores pour la musique / celui qui
occupe musicalement les nouveaux territoires sonores acquis par d’autres
(disons Scarlatti face à Bach, Varèse face à Boulez…).
J’ai plutôt choisi d’aggraver le défi en
circulant à l’inverse : de la musique vers les mathématiques, en vous
montrant comment un point de vue musicien peut éclairer une réflexion
mathématicienne (celle d’Alexandre Grothendieck dans Récoltes et Semailles). Je plaiderai ainsi, moins pour une raisonance musique-mathématiques [4],
que pour une connivence musicien-mathématicien [5].
Pour inscrire cette conférence sous le signe
d’une telle connivence, je la prononcerai debout (comme le font usuellement les
mathématiciens, là où les « littéraires » préfèrent lire un texte
assis) et en usant d’une craie sur le tableau noir plutôt que d’un affichage de
transparents…
*
L’objectif de cette conférence est très
délimité : il s’agit de dégager une dimension (parmi mille autres
également envisageables) du discours grothendieckien de Récoltes et Semailles, dimension que j’appellerai « musicalité ».
M’adressant à des mathématiciens, j’adopterai
autant que possible leur style d’exposition. Je poserai donc liminairement
ceci :
je
nomme musicalité un dynamique constituée par la circulation d’une place vide et constitutive d’une incorporation [6].
Je ne soutiendrai pas
·
que le texte Récoltes et Semailles ressemble à de la musique,
·
ou que Récoltes et Semailles parle de musique [7].
Je soutiendrai que Récoltes et Semailles thématise une dynamique qui relève d’une attention proprement mathématicienne
mais qui cependant peut également se penser comme « musicale ». Je
vais donc me servir d’un point de vue musicien sur ce qu’écouter musicalement
veut dire pour distinguer une strate du discours grothendieckien de Récoltes
et Semailles. Ce rapprochement m’a été suggéré par
Grothendieck lui-même quand il écrit (je ramasse son propos) :
« Ce qui fait la qualité du chercheur,
c’est la qualité de son attention à l’écoute de la voix des choses qui ne cessent
de se révéler à celui qui se soucie d’entendre. » (Récoltes et
Semailles 2.9)
ou lorsqu’il rapproche l’entendre du lire :
« Toutes les propriétés essentielles de
“la cohomologie” de la variété se “liraient” (ou s’“entendraient”)
déjà sur le motif correspondant. » (Récoltes et Semailles 2.16)
Je vais tenter de faire tout ceci sérieusement, c’est-à-dire en recourant là encore au mode d’exposition spécifique
du mathématicien : à une formalisation ad hoc (celle d’un taquin
rudimentaire apte à inscrire l’homologie en jeu dans mon sous-titre : musicalité
de Récoltes et Semailles).
*
Point de méthode.
J’aborde ici Récoltes et Semailles comme un texte qui relève
·
ni de la mathématique proprement dite –
il ne s’agit pas là d’un texte mathématique tel celui des EGA ou des SGA…
- ;
·
ni de la philosophie proprement dite (je
renvoie l’argumentation détaillée de ce point à d’autres textes)
·
mais très exactement de ce que j’appelle
une intellectualité mathématique.
Je nomme intellectualité mathématique un effort de discursivité (dans la langue vernaculaire de tout un
chacun) pour dire la mathématique de l’intérieur de son faire. Disons, plus
simplement : une manière de réfléchir en mathématicien la pensée
mathématique en la projetant dans le médium du langage ordinaire, une manière
de mettre des mots sur l’expérience mathématique du mathématicien.
Cette catégorie d’intellectualité mathématique
me vient directement de celle d’intellectualité musicale.
Je nomme intellectualité musicale un discours entreprenant de dire la musique dans la langue commune, de
projeter la pensée musicale (non langagière !) dans la langue commune, de mettre
des mots sur l’expérience musicale du musicien.
Pour situer rapidement la chose,
l’intellectualité musicale naît à mon sens avec Rameau (très précisément autour
de 1750). Au XIX° siècle, les intellectualités musicales notables sont celles
de Schumann, Berlioz et Wagner. Au xx°
siècle, elles prolifèrent avec Schoenberg, Hindemith, puis d’un côté la
filiation Krenek→Babbitt, et de l’autre la génération sérielle
Boulez-Stockhausen-Barraqué-Pousseur-Boucourechliev [8].
Sans trop m’étendre ici [9],
l’intellectualité musicale se distingue radicalement de la musicologie
(celle-ci organise des savoirs sur la musique en extériorité objectivante quand
l’intellectualité musicale réfléchit des connaissances en musique selon une
intériorité subjectivante). Elle se structure autour de trois pôles
enchevêtrés :
1) un pôle théorique - il y s’agit de
théoriser musicalement la musique (exemple
canonique : Rameau) ;
2) un pôle critique - il y s’agit
d’évaluer musicalement les œuvres et leurs
généalogies (exemple canonique : Boulez) ;
3) un pôle esthétique (en un sens non
philosophique du terme) - il y s’agit de caractériser musicalement les rapports de la musique à son extérieur : société, autres
modes de pensée… (exemple canonique : Wagner).
Il faudrait sans doute explorer non moins
systématiquement l’hypothèse d’une intellectualité mathématique à l’œuvre,
depuis le xx° siècle au moins (en
la distinguant aussi soigneusement de l’épistémologie qu’il convient de
distinguer l’intellectualité musicale de la musicologie).
J’ai amorcé une telle réflexion à propos
d’Henri Poincaré et d’Hermann Weyl [10].
On pourrait également le faire à l’endroit d’Alexandre Grothendieck en se
demandant, par exemple, quelles sont les spécificités de son intellectualité
mathématique ; on devrait alors se demander ce que les pôles onto-théorique, logique et esthétique [11] y ont de
propre…
Mais j’ai ici un objectif moins général :
il s’agit pour moi de dégager, dans cette intellectualité mathématique
singulière, une dimension particulière susceptible d’être nommée
« musicalité ».
Je vais pour ce faire extraire de Récoltes
et Semailles – plus singulièrement de sa première
partie (le « Prélude » de janvier 1986) – les composantes de cette
dynamique.
*
Le fil conducteur de la formalisation que je
vais vous proposer est le suivant : je vais partir d’une formalisation construite
pour rendre compte de la dynamique musicale de l’écoute et me demander ensuite
s’il est possible d’extraire de Récoltes et Semailles un autre modèle de cette même formalisation.
L’idée, tirée de la théorie mathématique des
modèles [12], est donc
de dégager un modèle hérétique pour une théorie existante – en l’occurrence
celle ayant l’écoute musicale pour modèle canonique -. On peut diagrammatiser
ainsi le propos : on part d’une théorie existante, bâtie pour un modèle
canonique (ici l’écoute musicale)
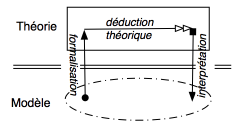
puis on greffe à cette théorie un modèle
hérétique :
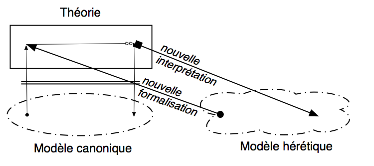
Quelle est la formalisation que je vais ici
mobiliser ?
J’en présenterai d’abord la syntaxe, puis la
sémantique « canonique » (correspondant au modèle de l’écoute
musicale).
Syntaxe
Il s’agit d’un petit taquin très élémentaire,
circulaire et à trois places [13].
Les taquins les plus connus ont celle
allure :

Le nôtre se présentera ainsi :
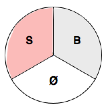
Il est fait de trois cases et de deux pièces
(que je distingue de deux lettres S et B), la case vide [14]
étant indexée d’un classique Ø.
La dynamique du taquin tient à la rotation de
sa case vide que je réaliserai canoniquement dans le sens
trigonométrique :
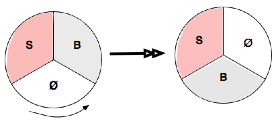
Les deux pièces étant ici distinguées, il faut
deux tours de la case vide pour obtenir un retour à la position de départ (il
suffirait d’un seul tour si les deux pièces étaient par contre indiscernables),
ce qui correspond au parcours complet d’une bande de Möbius :
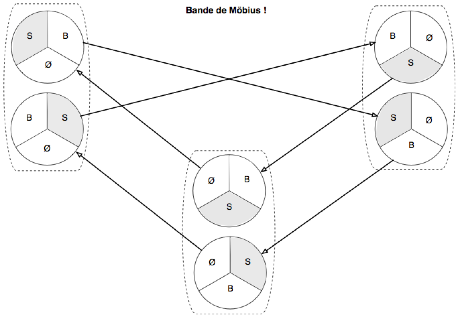
Sémantique
La sémantique « canonique » sera
celle-ci :
1) Chaque case se trouve ainsi nommée :
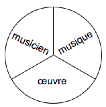
2) Les pièces S et B sont interprétées comme
source et but d’une transformation :
S → B
3) La disposition des pièces S et B sur deux
des trois cases {musicien, musique, œuvre} est
alors interprétée selon l’exemple suivant :
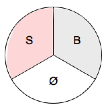
=
{musicien → musique}
qui signifiera : « le musicien fait
de la musique ».
À l’inverse, la disposition suivante
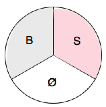
sera ainsi interprétée canoniquement :
{musique → musicien}. Soit : « la musique fait le musicien » [15].
On peut, à partir de là, théoriser l’écoute
musicale comme tourniquet entre les six dispositions de ce taquin.
Mon hypothèse de lecture de Récoltes et
Semailles consiste alors à nous demander si l’on peut
y repérer une dynamique analogue : une manière de rendre compte du travail
mathématique qui soit modèle de cette même formalisation et qui caractérise
alors la musicalité de ce texte de mathématicien ?
J’exploiterai pour ce faire le petit florilège
suivant, constitué sur la seule base des deux premières parties de Récoltes
et Semailles.
Florilège [Prélude]
·
Je me suis vu
amené à dégager et à dire des choses qui jusque là étaient toujours restées
dans le non-dit. [1]
·
C’est des choses
qui n’ont rien de technique. [1]
·
Dans Récoltes
et Semailles, je parle du
travail mathématique. C’est un travail que je connais bien et de première main.
La plupart des choses que j’en dis sont vraies, sûrement, pour tout travail
créateur, tout travail de découverte. [1]
·
La passion
d’amour est, elle aussi, pulsion de découverte. [1]
·
Au cours de la Promenade, il sera surtout question du travail
mathématique lui-même. [1]
·
Les problèmes de
maths […] qui se trouvaient dans le livre […] tombaient un peu trop du ciel,
comme ça à la queue-leue-leue, sans dire d’où ils venaient ni où ils allaient.
C’étaient les problèmes du livre, et pas mes problèmes. [2.1]
·
Quand une chose
me “tenait”, je ne comptais pas les heures ni les jours que j’y passais, quitte
à oublier tout le reste ! [2.1]
·
Mon énergie
était suffisamment absorbée à tenir la gageure que je m’étais proposé :
développer une théorie qui me satisfasse pleinement. [2.1]
·
L’intuition du
volume […] ne pouvait qu’être le reflet d’une réalité, élusive pour le moment,
mais parfaitement fiable. C’est cette réalité qu’il s’agissait de saisir, tout
simplement. [2.1]
·
La mathématique
est une chose illimitée en étendue et en profondeur. [2.1]
·
J’étais un
mathématicien : quelqu’un qui “fait” des maths, au plein sens du terme -
comme on “fait” l’amour. [2.2]
·
Je sais aussi
quel est le signe que je suis entendu. C’est quand, au delà de toutes les
différences de culture et de destin, ce que je dis de ma personne et de ma vie
trouve en toi [lecteur] écho et résonance. [2.2]
·
Je me sens faire
partie, quant à moi, de la lignée des mathématiciens dont la vocation spontanée
et la joie est de construire sans cesse des maisons nouvelles. [2.5]
·
Je viens là
d’esquisser à grands traits deux portraits : celui du mathématicien
“casanier” qui se contente d’entretenir et d’embellir un héritage, et celui du
bâtisseur-pionnier, qui ne peut s’empêcher de franchir sans cesse ces “cercles
invisibles et impérieux” qui délimitent un Univers. On peut les appeler aussi,
par des noms un peu à l’emporte-pièce mais suggestifs, les “conservateurs” et
les “novateurs”. L’un et l’autre ont leur raison d’être et leur rôle à jouer,
dans une même aventure collective se poursuivant au cours des générations, des
siècles et des millénaires. Dans une période d’épanouissement d’une science ou
d’un art, il n’y a entre ces deux tempéraments opposition ni antagonisme. [2.5]
·
Si j’ai excellé
dans l’art du mathématicien, c’est moins par l’habileté et la persévérance à
résoudre des problèmes légués par mes devanciers, que par cette propension
naturelle en moi qui me pousse à voir des questions, visiblement cruciales, que
personne n’avait vues, ou à dégager les “bonnes notions” qui manquaient […]
ainsi que les “bons énoncés” auxquels personne n’avait songé. [2.6]
·
Mais plus encore
que vers la découverte de questions, de notions et d’énoncés nouveaux, c’est
vers celle de points de vue féconds, me conduisant constamment à introduire, et
à développer peu ou prou, des thèmes entièrement nouveaux, que me porte mon
génie particulier. C’est là, il me semble, ce que j’ai apporté de plus
essentiel à la mathématique de mon temps. À vrai dire, ces innombrables
questions, notions, énoncés dont je viens de parler, ne prennent pour moi un
sens qu’à la lumière d’un tel “point de vue”. [2.6]
·
Le point de vue
fécond est celui qui nous révèle, comme autant de parties vivantes d’un même
Tout qui les englobe et leur donne un sens, ces questions brûlantes que nul ne
sentait. [2.6]
·
Ce sont les
points de vue féconds qui sont, dans notre art, les plus puissants outils de
découverte - ou plutôt, ce ne sont pas des outils, mais ce sont les yeux même
du chercheur qui, passionnément, veut connaître la nature des choses mathématiques.
[2.6]
·
Il arrive,
parfois, qu’un faisceau de points de vue convergents […] donne corps à une
chose nouvelle. [2.6]
·
Rarement ai-je
pris le loisir de noter noir sur blanc […] le maître-plan invisible à tous […]
sauf à moi, qui au cours des jours, ces mois et années guidait ma main avec une
sûreté de somnambule. [2.7]
·
Parmi les
nombreux points de vue nouveaux que j’ai dégagés en mathématique, il en est
douze, avec le recul, que j’appellerais des “grandes idées”. [2.8]
·
J’étais pris
alors par la fascination de ce qui m’appelait… [2.8]
·
C’est bien cette
harmonie, non encore apparue mais qui sûrement “existait” déjà bel et bien,
quelque part dans le giron obscur des choses encore à naître – c’est bien elle
qui a suscité tour à tour ces thèmes qui n’allaient prendre tout leur sens que
par elle, et c’est elle aussi qui déjà m’appelait à voix basse et pressante.
[2.8]
·
Une vision
nouvelle est une chose si vaste, que son apparition ne peut sans doute se
situer à un moment particulier, mais qu’elle doit pénétrer et prendre
possession progressivement pendant de longues années, si ce n’est sur des générations,
de celui ou de ceux qui scrutent et qui contemplent. [2.8]
·
Jusqu’à il y a
deux ans encore ma relation à la mathématique se bornait (mis à part la tâche
de l’enseigner) à en faire. [2.8]
·
Je me rappelle
encore de cette impression saisissante (toute subjective certes), comme si je
quittais des steppes arides et revêches, pour me retrouver soudain dans une
sorte de “pays promis” aux richesses luxuriantes, se multipliant à l’infini
partout où il plaît à la main de se poser, pour cueillir ou pour fouiller… Et
cette impression de richesse accablante, au delà de toute mesure , n’a
fait que se confirmer et s’approfondir au cours des ans, jusqu’à aujourd’hui
même. [2.9]
·
C’est pour
exprimer, le plus fidèlement que nous le pouvons, ces choses que nous sommes en
train de découvrir et de sonder, et cette structure réticente à se livrer, que
nous essayons à tâtons, et par un langage encore balbutiant peut-être, à
cerner. [2.9]
·
Ce qui fait la
qualité de l’inventivité et de l’imagination du chercheur, c’est la qualité de
son attention, à l’écoute de la voix des choses. Car les choses de l’Univers ne
se lassent jamais de parler d’elles-mêmes et de se révéler, à celui qui se
soucie d’entendre. [2.9]
·
J’ai fait
confiance simplement, comme par le passé, à l’humble voix des choses. [2.11]
·
Le pouvoir
rénovateur en nous n’est autre que l’innocence. [2.11]
·
C’est le point de
vue des faisceaux qui a été le guide silencieux et sûr. [2.13]
·
Je ne vois
personne d’autre sur la scène mathématique, au cours des trois décennies
écoulées, qui aurait pu avoir cette naïveté, ou cette innocence, de faire (à ma
place) cet autre pas crucial entre tous, introduisant l’idée si enfantine des topos.
[…] Je ne vois personne d’autre, […] qui aurait eu […] la foi, pour mener à
terme cette humble idée. [2.14]
·
C’est un pays
peut-être où il n’y a plus d’enfants pour mener boire les chevaux, et où les
chevaux ont soif, faute d’un gamin qui retrouve le chemin qui mène à la
rivière… [2.15]
·
Dans mon travail
de mathématicien, je vois à l’œuvre surtout ces deux forces ou pulsions,
également profondes, de nature (me semble-t-il) différentes. Pour évoquer l’une
et l’autre, j’ai utilisé l’image du bâtisseur, et celle du pionnier ou de
l’explorateur. [2.17]
·
Quand je “bâtis
des maisons”, c’est le “connu” qui domine, et quand “j’explore”, c’est
l’inconnu. Ces deux “modes” de découverte, ou pour mieux dire, ces deux aspects
d’un même processus ou d’un même travail, sont indissolublement liés. Ils sont
essentiels l’un et l’autre, et complémentaires. Dans mon travail mathématique,
je discerne un mouvement de va-et-vient constant entre ces deux modes
d’approche. [2.17]
·
Ce que je dis
ici sur le travail mathématique est vrai également pour le travail de
“méditation” (dont il sera question un peu partout dans Récoltes et Semailles). Il n’y a guère de doute pour moi que c’est
là une chose qui apparaît dans tout travail de découverte, y compris dans celui
de l’artiste (écrivain ou poète, disons). [2.17]
·
Essayant dans
ces pages de cerner ce que j’ai apporté de plus essentiel à la mathématique de
mon temps, par un regard qui embrasse une forêt, plutôt que de s’attarder sur
des arbres - j’ai vu, non un palmarès de “grands théorèmes”, mais un vivant
éventail d’idées fécondes, venant concourir toutes à une même et vaste vision.
[2.17]
·
“L’enfant” et
“le bâtisseur” étaient un seul et même personnage. Ce nom est donc devenu, plus
simplement, “L’enfant bâtisseur”. [2.18]
·
J’ai commencé
par l’introduire sous le nom flamboyant de “pionnier”, suivi de celui, plus
terre-à-terre mais encore auréolé de prestige, d’“explorateur”. [2.18]
·
Tu es l’enfant,
issu de la Mère, abrité en Elle, nourri de Sa puissance. Et l’enfant s’élance
de la Mère, la Toute-proche, la Bien-connue - à la rencontre de la Mère,
l’Illimitée, à jamais Inconnue et pleine de mystère… [2.18]
On peut dans Récoltes et Semailles repérer clairement trois instances.
1) L’instance du mathématicien.
Elle est inscrite au cœur de ce texte qui
entreprend explicitement de réfléchir le travail du mathématicien Alexandre Grothendieck.
Le mathématicien y est doublement saisi :
·
comme celui qui fait de la mathématique (working mathematician), soit la flèche
mathématicien
→ mathématiques
·
mais également comme celui qui est modelé
par la situation mathématique sur laquelle il travaille, selon la figure cette
fois passive d’un Yin ; soit cette fois la flèche
→
mathématicien
Remarque : je
ne me prononcerai pas ici sur la véridicité de ce que Grothendieck nous énonce
dans Récoltes et Semailles, en particulier à son
endroit. Alexandre Grothendieck était-il bien, entre 1954 et 1970, pour
l’essentiel en position féminine au regard des mathématiques (comme il nous le
déclare bien plus tard en 1986) ? La question ici n’est pas là : je
travaille sur un discours, pour en dégager une figure intelligible du travail
mathématique, non pour évaluer quelle a été la vie d’Alexandre G.
Au total, le mathématicien se trouve
explicitement l’enjeu d’un va-et-vient entre une position active et une
position passive, va-et-vient que Grothendieck aime à présenter comme une
pulsation Yang/Yin.
La thèse de Grothendieck est que l’aspect
principal de cette opposition est du côté passif (Yin) – celui qu’il dit
relever d’une position d’enfant - si bien que la
synthèse [16] du
va-et-vient doit être nommé une passivité active, celle que pour sa part
Grothendieck dénomme « enfant bâtisseur »
(2.18) ou « somnambulisme » (2.7).
Cette passivité active s’applique
exemplairement aux rapports du mathématicien à la mathématique :
mathématique→mathématicien
{la mathématique fait le mathématicien, le constitue comme tel}
mathématicien→mathématique
{le mathématicien fait de la mathématique}
ce qu’Alexandre Grothendieck métaphorise
ainsi :
« L’enfant
s’élance de la Mère… à la rencontre de la Mère » !
(2.18)
2) La deuxième instance est donc celle de la mathématique.
La mathématique se trouve avant tout en
position de source S (active, génératrice) : elle est un univers aux
paysages inépuisables ; elle est une Mère-matrice qui engendre le
mathématicien.
Mais la mathématique est aussi ce qui est
transformé par les maisons qu’on y construit, par les territoires qu’on y explore
et défriche ; la mathématique est aussi ce qui est fécondé par le travail
et les idées des mathématiciens ; la mathématique est aussi un pays que
l’activité des hommes transforme en succession de paysages. Elle est donc
également un but et pas seulement une source :
→
mathématique →
3) La troisième instance apparaît moins
immédiatement dans Récoltes et Semailles :
c’est celle des « points de vue féconds », des
« idées-forces », des douze grands thèmes grothendieckiens ; je
la nommerai l’instance de la théorie (mathématique).
La théorie (mathématique), c’est la maison que
construit le mathématicien :
mathématicien→théorie
C’est tout autant l’idée-force qui le
guide :
théorie→mathématicien
Grothendieck réunit ces trois instances sous
la forme de cette très belle image d’« un pays
[la mathématique] où les enfants [les mathématiciens]
mènent boire les chevaux [les théories] »
(2 .15).
On se retrouve donc avec un diagramme à trois
termes (ou « objets ») reliés en l’état selon les
« morphismes » suivants :
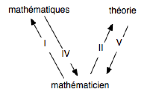
que je formulerai ainsi (selon un numérotage
dont le principe s’éclaircira plus loin) :
I : le mathématicien fait de la
mathématique.
IV : la mathématique constitue le
mathématicien.
II : le mathématicien s’incorpore à la
théorie.
V : la théorie passionne le musicien.
Restent donc, pour compléter ce diagramme, les
deux morphismes supplémentaires entre mathématique et théorie
![]()
que Grothendieck thématise ainsi :
·
La théorie agit la mathématique, la
laboure : c’est l’image des chevaux qui paissent et modèlent ainsi le
paysage.
·
La mathématique est « à la
théorie » (comme on peut dire que la musique est « à l’œuvre »
en entendant ainsi à la fois qu’elle est affaire d’œuvre et que l’œuvre est
affaire de musique) au sens où la mathématique n’existe effectivement que comme
déploiement et développement de théories (et non pas comme ensemble statique de
résultats et de formules à appliquer).
D’où le diagramme complet suivant :
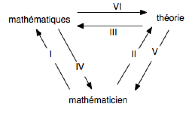
I : le mathématicien fait de la
mathématique.
II : le mathématicien s’incorpore à la
théorie.
III : la mathématique est à la
théorie.
IV : la mathématique constitue le
mathématicien.
V : la théorie passionne le
mathématicien.
VI : la théorie agit la mathématique.
Rendu en ce point, l’idée simple va être de
transformer ce diagramme en un diagramme dual (au sens de la dualité des
graphes) par interversion entre ses sommets et ses flèches. On prendra ici
simplement soin de dédoubler chaque sommet selon qu’il est source ou but selon
le principe suivant :
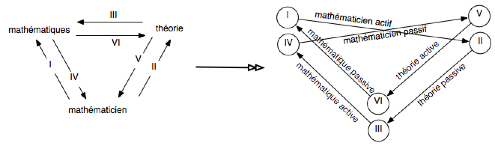
Le sens de parcours de notre diagramme dual se
fait par pivotement alterné sur une position active puis sur une autre position
passive (transformation d’un but pour une même source, puis d’une source pour
un même but) :
mathématicien
actif (I-II) / théorie passive (II-III) / mathématique active (III-IV) /
mathématicien passif (IV-V) / théorie active (V-VI) / mathématique passive
(VI-I)…
On peut alors formaliser notre diagramme selon
notre précédent taquin, en interprétant cette fois ainsi ses trois cases :
On formalise au total le parcours möbiusien
suivant :
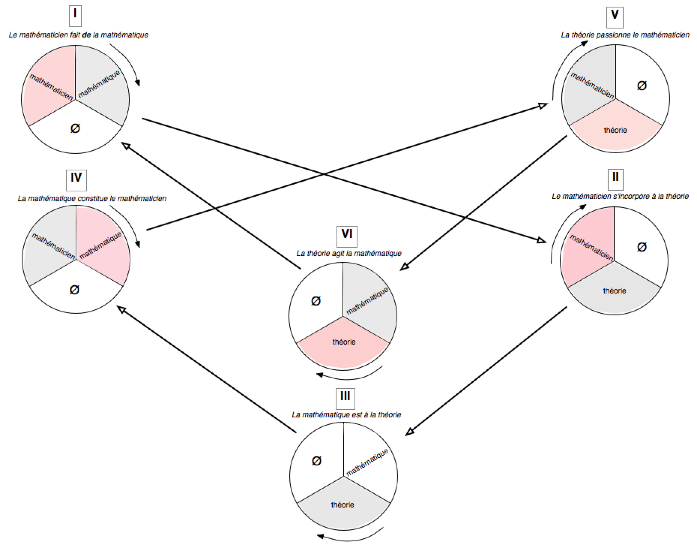
On peut alors résumer cette dynamique en une
seule phrase [17] :
le mathématicien
fait de la mathématique
en s’incorporant à une
théorie
irriguée
par cette même mathématique
laquelle
constitue ce mathématicien
passionné
par la théorie précédente
qui
se trouve agir la mathématique
que
fait le mathématicien !
Ce tourniquet est isomorphe au tourniquet de
l’écoute musicale [18]
s’il est vrai que l’écoute musicale consiste à se trouver incorporé contre soi
(contre sa part individuelle, engluée dans la simple audition [19])
à la passivité active de l’interprète qui prête son corps à l’œuvre pour faire
exister la musique qu’elle agit.
Il y a donc bien musicalité de Récoltes et
Semailles. Cqfd.
*
Ce rapprochement me suggère ultimement la
remarque suivante : une théorie mathématique ne se réduit pas à tel ou tel
texte mathématique, pas plus qu’une œuvre musicale ne se réduit à sa partition.
Une théorie mathématique n’existe vraiment que comprise non pas comme
consécution logique informatisable mais comme dynamique de pensée que l’on
épouse pour la prolonger. À ce titre, comprendre le rôle d’une démonstration
dans une théorie mathématique donnée, c’est un peu comme comprendre une œuvre
musicale (soit l’écouter jouer).
Il est donc vrai que, comme Yves André le
soutient avec constance, la mathématique, sommet de l’intelligible, n’est pas
pour autant sans attache du côté du sensible.
––––