Intellectualité
mathématique & intellectualité musicale : convergences et divergences (à la lumière des écrits d’Henri
Poincaré et Hermann Weyl)
Séminaire mamuphi (mathématiques, musique & philosophie)
Ens, 14 octobre 2006
François Nicolas
(Ens : Collectif HPS, Laboratoire Pensée des sciences)
Résumé
Existe-t-il une
« intellectualité mathématique » comme il existe, depuis 1750
(Rameau), une intellectualité musicale (essentiellement Schumann, Wagner,
Schoenberg, Boulez) ? Quels en sont les traits constitutifs, les moments historiques
cruciaux, les principales délimitations, les grandes intensions… ?
On avancera sur ces points
quelques hypothèses à la lumière d’une relecture des écrits d’Henri Poincaré et
Hermann Weyl, en attachant une importance particulière à la clarification de la
manière dont cette intellectualité mathématique s’articule à la philosophie
proprement dite avec laquelle elle est le plus souvent confondue.
Pour ce faire, on distinguera
préalablement cette « intellectualité mathématique » du cas, tout à
fait singulier, des écrits de mathématiciens qui se trouvent être également des
philosophes (Russell, Whitehead…), comme des écrits de philosophes qui se
trouvent être également des mathématiciens (Descartes, Leibniz, Husserl…).
On appellera
« intellectualité mathématique » les efforts du mathématicien pensif
pour réfléchir, en intériorité et
dans la langue vernaculaire [1],
la spécificité de la pensée mathématique.
« Le risque de l’activité créatrice, quand elle n’est pas surveillée par la réflexion, est qu’elle dévie du sens, se fourvoie, cristallise en routine. […] Ce que nous avons fait ici, c’est de la réflexion. » Hermann Weyl (1930)
« Je ne partage pas le dédain de G. H. Hardy à l’égard
de celui qui “parle sur” [les mathématiques, etc…] L’activité créative non
contrôlée par la réflexion risque de se détacher de toute signification, de
perdre contact et perspective, de dégénérer en routine. » Hermann Weyl (1953)
À ce titre, cette réflexion
mathématicienne refuse de mettre la mathématique en position d’objet, saisi de
l’extérieur par un discours préconstitué, et se distingue ainsi de
l’épistémologie conçue comme discipline autonome et extérieure à son
« objet » [2] :
de même que l’intellectualité musicale se déploie en nouant, de l’intérieur de
la musique, une triple problématique (théorique, critique
et esthétique), de même
l’intellectualité mathématique s’avère nouer, de l’intérieur de la
mathématique, une triple problématique (qu’on proposera de nommer onto-théorique, logique
et esthétique) qui la fait
interagir successivement avec les autres sciences, la philosophie [3]
et les arts.
« Les mathématiques ont un triple but. Elles doivent
fournir un instrument pour l’étude de la nature. Mais ce n’est pas tout : elles
ont un but philosophique et, j’ose le dire, un but esthétique. » Henri Poincaré (1898)
À tous ces titres, on
explorera l’hypothèse que l’intellectualité mathématique se serait constituée
dans la seconde partie du XIX° siècle, sous la poussée des exigences réflexives
portées par la recomposition mathématique tant de la géométrie que de la
logique.
On tentera sur cette base une
première recension des principaux motifs de cette « intellectualité
mathématique » : un rapport spécifique à l’histoire des
mathématiques, une préoccupation didactique singulière (instruction et
éducation des jeunes mathématiciens comme des non-mathématiciens), l’examen
mathématicien des effets intra-mathématiques de la philosophie, etc.
On ne manquera pas de se
demander, in fine, à quel titre
cette réflexion se voit engagée sous le signe de l’intellectualité musicale,
par un musicien donc, qui se trouve à proprement parler n’être ni
mathématicien, ni philosophe.
On soutiendra que l’enjeu de
cet exercice est triple :
·
Il s’agit d’abord de
restaurer à la philosophie sa puissance singulière (sans la compromettre dans
la généralité creuse d’un discours prétendant parler de tout [4])
en sorte de préserver pour le musicien sa capacité de l’orienter dans la
pensée.
·
Il s’agit ensuite de
dégager la possibilité d’une capacité réflexive interne au champ mathématique
et d’exhausser ainsi la figure du mathématicien pensif (ou réflexif) comme interlocuteur possible pour le musicien pensif [5].
·
Il s’agit enfin d’une
nouvelle effectivité du principe (musicien) : « La musique ne pense
pas seule », en l’occurrence de la quête, en ce XXI° siècle naissant, de
nouveaux alliés pour une intellectualité musicale qui soit contemporaine du
front actuel de la mathématique et de la logique mathématisée.
Au total, il apparaîtra que ce
n’est donc pas tout à fait un hasard si cette réflexion musicienne tente de se
clarifier au moment même où des workings mathematicians acceptent de s’intéresser à une « école
mathématique pour musiciens et autres non-mathématiciens »…
–––––
I. Enjeux
et méthode
Objectif
Modèle
Récréation musicale préliminaire
Alliance à trois…
Rappel rapide
De la philosophie…
Deux figures de mathématicien
Autres possibles ?
II. Poincaré/Weyl
Distance prise d’avec la philosophie
Réponse : le pragmatisme du mathématicien
Que sont les mathématiques ?
Délimitations
Ontologie…
Une pensée…
De l’articulation entre mathématiques et physique mathématisée
De l’articulation entre mathématiques et logique mathématique
Situation de la mathématique dans la pensée
Distance prise avec une conception langagière de la pensée
Subjectivité de mathématicien
Le travail du mathématicien
Nécessité d’une intellectualité mathématique !
La dimension esthétique dans les mathématiques et dans le
travail du mathématicien
L’adresse aux non-mathématiciens
La mathématique concerne la pensée de tout un chacun
Le contenu de pensée de tel concept mathématique
III. Plus
synthétiquement…
Définition
Mathématicien pensif, ou réflexif
L’intellectualité mathématique n’est pas une affaire de
« traduction »
Différences mathématique/musique
Différences sciences/arts
Différence de rapport à la philosophie
Deux caractéristiques communes
La mathématique est la cible
Le mathématicien est celui qui fait des mathématiques
Thèmes, enjeux, intensions
Onto-théorie
Logique
Esthétique
Triple interlocution
Différents types d’intellectualité mathématique ?
L’anti-intellectualité mathématique
Deux hypothèses
Constitution de l’intellectualité mathématique dans la seconde
partie du 19° siècle
Aujourd’hui ?
Questions, objections et réponses
I. Enjeux et méthode
Objectif
Objectif très restreint : convaincre de l’émergence d’un type singulier de discours tenu par un certain nombre de mathématiciens - ceux des working mathematicians que j’appellerai « mathématiciens pensifs » -, type que je propose d’appeler « intellectualité mathématique ».
Il s’agit donc de faire émerger une figure singulière de discours et, pour cela, d’en distinguer les principaux traits caractéristiques, de faire des hypothèses quant à ses enjeux, son histoire, sa diversification interne (une éventuelle typologie).
Modèle
Modèle sera pris sur l’intellectualité musicale [6] : discours musicien né en 1750 puis déployé par Schumann, Wagner, Schoenberg, Boulez…
L’enjeu est une alliance possible entre intellectualités musicale et mathématique, par-delà la simple mathématique appliquée à la musique et – beaucoup mieux ! - les théories mathématiques de la musique (par exemple Mazzola).
Récréation musicale préliminaire
De même qu’on réduit souvent les mathématiques à un pur calcul (comme si le mathématique était le calculable), de même on réduit souvent la musique à un pur jeu sonore (comme si le musical était le sonore organisé).
Pour donner une preuve par l’exemple négatif, on peut écouter les transcriptions sonores effectuées de quelques déductions logico-mathématiques [7]– je vous laisse juge - :
— le principe d’identité donne ceci :

— le « théorème x=x » donne ceci :

— le « théorème 2+2=4 » donne ceci :
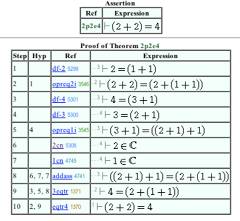
Où l’on voit que, de même que démonstration mathématique ≠ déduction logique, de même développement musical ≠ organisation sonore : l’organisation sonore indéniable de ces exemples n’est tout simplement pas musicale !
Alliance à trois…
Importance, me semble-t-il, d’une alliance entre mathématiques, musique et philosophie au seuil du XXI° siècle.
Rappel rapide
· nœud (quasi borroméen) au VI° siècle av. J.-C. : le moment grec
· dénouage du côté de la musique avec Aristoxène de Tarente (IV° siècle av. J.-C.) : première théorie musicienne de la musique
· renouage, cette fois direct, entre musique et philosophie avec St Augustin
· renouage à trois chez Descartes (mais non borroméen : cf. musique-philosophie-mathématiques)
· invention de l’intellectualité musicale par Rameau, très exactement à partir de 1750 : quand il ne se contente plus d’une théorie musicienne de la musique et qu’il prend ses distances d’avec Descartes
Ensuite, l’intellectualité musicale ne se déploiera plus guère sous l’horizon mathématique.
Aujourd’hui, deux nouveautés (peut-être !) :
1) l’intellectualité musicale est dégagée comme telle : nommée, identifiée…
2) peut-être le temps est-il venu, au seuil du XXI° siècle, d’un nouveau nouage à 3 dont le titre même de notre séminaire mamuphi atteste (j’aurais préféré mumaphi !)
De la philosophie…
C’est dire que dans les rapports intellectualité musicale (IM) / intellectualité mathématique (IƐ), la philosophie (φ) joue un rôle clef, non seulement dans un éventuel nouage à 3 mais plus encore de manière interne : l’intellectualité musicale s’est constituée par distance subjective prise d’avec la philosophie (cf. Rameau par rapport à Descartes à partir de 1750 : voir la différence entre le premier et le second Rameau).
D’où l’importance particulière d’examiner les rapports de l’intellectualité mathématique (IƐ) avec la philosophie (φ). On verra en effet que IƐ/φ≠IM/φ
Cependant investigation par analogie : convergences ? divergences ?
Deux figures de mathématicien
Examen de deux figures particulières :
· celle d’Henri Poincaré (1854-1912)
· celle d’Hermann Weyl (1885-1955)
Hypothèse : leur place éminente dans la constitution d’une telle intellectualité mathématique. D’où l’examen non de leurs travaux proprement mathématiques mais de leurs ouvrages « didactiques » et « réflexifs », pensifs.
Cf. pour Poincaré :
· La Science et l’hypothèse (1902) [Réf. : P.-I]
· La Valeur de la Science (1905) [Réf. : P.II]
· Science et méthode (1908)
· Dernières pensées (1913)
· Recueil
d’articles (1891-1911) : L’analyse et la recherche
Je me réfèrerai aujourd’hui aux deux premiers.
Cf. pour Weyl :
· Le continu et autres écrits (Recueil de textes ; Vrin 1994) [Réf. : W.]
· Symétrie et mathématique moderne (1951)
Je me réfèrerai aujourd’hui au premier.
Autres possibles ?
Y aurait-il d’autres mathématiciens possibles ? Hadamard ? Thom ? Penrose ?
J’élimine :
· les mathématiciens et/ou logiciens qui sont aussi explicitement des philosophes : Bolzano, Russell, Whitehead…
· les philosophes qui sont aussi explicitement des mathématiciens : Descartes, Leibniz, Husserl…
· les mathématiciens qui n’ont parlé sur la mathématique que marginalement – je les appellerai des intervenants - : par exemple André Weil, Laurent Schwartz, ou Alain Connes.
· Cas particulier : Grothendieck ? Il me semble qu’il y a une trop grande séparation chronologique entre ses écrits proprement mathématiques et sa réflexion mathématicienne pour le retenir (mais ce serait à discuter).
À proprement parler, je ne trancherai pas la question de savoir si Poincaré et Weyl, mathématiciens indiscutables, peuvent être aussi tenus par certains de leurs travaux pour de véritables philosophes (cf. thèse de Gabriella Crocco à Cerisy…). S’ils l’étaient (ce que je ne crois pas [8]), mon propos garderait pour objectif de dégager dans leurs écrits un type singulier de discours qui n’est ni le discours mathématique proprement dit, ni un éventuel discours philosophique.
II. Poincaré/Weyl
S’agissant d’introduire à la catégorie d’intellectualité mathématique, je vais moins insister sur la différence entre Poincaré et Weyl que sur leurs traits communs, du moins sur ceux qui permettent de discerner la consistance discursive recherchée.
Commençons donc par une recension désordonnée de thèmes, de préoccupations chez ces deux mathématiciens.
*
Je propose de repérer les traits suivants, que j’indexerai de citations prélevées dans :
· Poincaré : La Science et l’hypothèse [P.-I]
· Poincaré : La Valeur de la Science [P.II]
· Weyl : Le continu et autres écrits [W.]
Distance prise d’avec la philosophie
Soit un souci de se dégager d’une préoccupation d’ordre strictement philosophique, souci qui les conduit alors à caractériser en extériorité cette philosophie comme « métaphysique ».
Poincaré
Je n’emploie jamais le verbe percevoir, ni le substantif
perception parce que je ne sais pas ce qu’ils veulent dire. J’ignore si la
perception est une sensation ou un jugement, et je crois voir que les
philosophes qui emploient ce mot l’entendent les uns dans le premier sens,
les autres dans le second. C’est pourquoi j’évite de l’employer. [Lettre au directeur de Mind (1906) en réponse aux
critiques de Russell] (P.-I.13)
Un philosophe, bien sûr, n’éviterait pas la question de la perception…
Pourquoi une si longue préparation est-elle nécessaire pour
s’habituer à cette rigueur parfaite [des mathématiques], qui, semble-t-il,
devrait s’imposer naturellement à tous les bons esprits ? C’est là un
problème logique et psychologique bien digne d’être médité. Mais nous nous
y arrêterons pas ; il est étranger à notre objet [« Sur la nature du raisonnement mathématique »]. (P.-I.35)
notre objet… de mathématicien
Quand on dit que la force est la cause d’un mouvement, on
fait de la métaphysique, et cette définition, si l’on devait s’en
contenter, serait absolument stérile. (P.-I.118)
« Stérile » pour qui ? Pour le savant et le mathématicien…
Dans l’hypothèse déterministe, [la loi de conservation de
l’énergie] apparaîtrait comme une limite imposée à la liberté. Mais ce mot
m’avertit que je m’égare et que je vais sortir du domaine des mathématiques et
de la physique. (P.-I.148)
… pour entrer dans celui de la philosophie !
Les théories mathématiques n’ont pas pour objet de nous
révéler la nature des choses ; ce serait là une prétention déraisonnable.
Leur but unique est de coordonner les lois physiques que l’expérience nous fait
connaître, mais que sans le secours des mathématiques nous ne pourrions même
énoncer. Peu nous importe que l’éther existe réellement, c’est l’affaire des métaphysiciens ;
l’essentiel pour nous c’est que tout se passe comme s’il existait et que cette
hypothèse est commode pour l’explication des phénomènes. Après tout, avons-nous
d’autre raison de croire à l’existence d’objets matériels ? Ce n’est là aussi
qu’une hypothèse commode. (P.-I.215)
Pragmatisme contre métaphysique
Un jour viendra peut-être où les physiciens se
désintéresseront de ces questions [départager entre différentes explications
que l’expérience ne peut trancher], inaccessibles aux méthodes positives, et
les abandonneront aux métaphysiciens. Ce jour n’est pas venu. (P.-I.225)
Net partage subjectif entre savants et métaphysiciens
Les philosophes font une objection… […] « Et après ? disent les
philosophes… […] Est-ce à dire qu’il n’y a rien à retenir de cette
objection des philosophes ? Ce n’est pas cela que je veux
dire… » (P.-II.34)
Cf. dialogue explicite avec les philosophes, en extériorité subjective : il ne se compte clairement pas pour philosophe.
C’est là l’affaire du psychologue et du métaphysicien et je ne discuterai pas cette question [de savoir si l’intuition pure saurait ou non se passer du secours des sens]. (P.-II.39)
Il se déclare subjectivement extérieur à cela…
Weyl
Il va de soi qu’il faudrait ici une analyse phénoménologiquement approfondie de la notion d’existence. (W.-126)
Cf. l’intellectualité mathématique n’est pas la philosophie (sous l’espèce d’une phénoménologie)
Les mathématiques ont manifesté leur entière participation à la révolte d’esclaves des sciences positives contre la philosophie. (W.-165)
Là encore mathématiques et philosophie font deux.
Je n’entrerai pas dans de grandes discussions afin de vous convertir à cette opinion de Brouwer [la définition d’une somme finie ne détermine pas a priori le sens d’une somme infinie]. C’est entièrement une affaire de réflexion, qui n’a rien à voir avec des théories épistémologiques, voire métaphysiques, ni avec de quelconques axiomes arbitrairement nommés mathématiques, ni avec leurs manipulation techniques. (W.-166)
Écart de la « réflexion » par rapport à la philosophie (épistémologie + métaphysique)
La nature de la vérité dans les théories physiques est un problème philosophique ou épistémologique plutôt qu’un problème physique. (W.-171)
Je n’ose imaginer qu’un mathématicien aurait le courage d’en éluder l’honnête solution [un problème de jeu dont von Neumann a montré la finitude] en mettant en avant un dogme métaphysique. (W.-179)
Le mathématicien ne fait pas de métaphysique.
Aristote en fait parle de la métaphysique plutôt que des mathématiques. (W.-268)
Depuis toujours la métaphysique a tenté de surmonter le dualisme de l’objet et du sujet, de l’être et du possible, de l’être et du sens, de la contrainte et de la liberté. (W.-298)
Cf. sa caractérisation de la philosophie comme « métaphysique » extérieure à son propos…
Les mathématiques elles aussi, soit de leur propre mouvement, soit en dépendance de la philosophie, n’ont pas résisté à cet attrait de l’absolu. (W.-298)
Il s’agit aussi pour lui de réfléchir en mathématicien les effets intra-mathématiques de la philosophie.
Réponse : le pragmatisme du mathématicien
Poincaré
Une géométrie ne peut pas être plus vraie qu’une autre ; elle peut seulement être plus commode. (P.-I.76) La géométrie n’est pas vraie, elle est avantageuse. (P.-I.108)
Peu nous importe que l’éther existe réellement, c’est
l’affaire des métaphysiciens ; l’essentiel pour nous c’est que tout se
passe comme s’il existait et que cette hypothèse est commode pour l’explication
des phénomènes. Après tout, avons-nous d’autre raison de croire à l’existence
d’objets matériels ? Ce n’est là aussi qu’une hypothèse commode. (P.-I.215)
Je n’ai pas l’intention de traiter ici la question de la contingence des lois de la nature, qui est évidemment insoluble, et sur laquelle on a déjà tant écrit. Je voudrais seulement faire remarquer que de sens différents on a donné à ce mot de contingence et combien il serait utile de les distinguer. (P.-II.171)
Pragmatisme, évitant explicitement les discussions proprement philosophiques sur un « mot » (le concept philosophique est traité comme un simple mot dont on décidera conventionnellement de l’usage…).
Que sont les mathématiques ?
Un souci de caractériser ce que sont les mathématiques (ce qui ne veut nullement dire les définir) pour mieux comprendre comment il est possible qu’elles aient l’efficacité et l’applicabilité qu’on leur connaît.
Délimitations
Poincaré
Le véritable continu mathématique est tout autre chose que celui des physiciens et celui des métaphysiciens. (P.-I.48)
La mathématique a (doit avoir) sa vision propre du continu.
On vous a sans doute souvent demandé à quoi servent les mathématiques […]. Parmi les personnes qui font cette question, je dois faire une distinction ; les gens pratiques réclament seulement de nous le moyen de gagner de l’argent. Ceux-là ne méritent pas qu’on leur réponde ; c’est à eux plutôt qu’il conviendrait de demander à quoi bon accumuler tant de richesses et si, pour avoir le temps de les acquérir, il faut négliger l’art et la science qui seuls nous font des âmes capables d’en jouir et propter vitam vivendi perdere causas. D’ailleurs une science uniquement faite en vue des applications est impossible ; les vérités ne sont fécondes que si elles sont enchaînées les unes aux autres. (P.-II.104)
Caractériser les mathématiques par leur sens…
Je veux défendre la Science pour la Science. […] Ce
n’est que par la Science et par l’Art que valent les civilisations. On s’est
étonné de cette formule : la Science pour la Science ; et pourtant
cela vaut bien la vie pour la vie, si la vie n’est que misère. (P.II-186)
Les mathématiques valent pour elles-mêmes.
Ontologie…
Poincaré
Pour Poincaré : ontologie/ontique ou Être/étants=Forme/matières (la Forme de l’Être / les matières des étants)
Ce que [la science] peut atteindre, ce ne sont pas les choses elles-mêmes, comme le pensent les dogmatiques naïfs, ce sont seulement le rapport entre les choses ; en dehors de ces rapports, il n’y a pas de réalité connaissable. (P.-I.25) Les mathématiciens n’étudient pas des objets, mais des relations entre les objets ; il leur est donc indifférent de remplacer ces objets par d’autres, pourvu que les relations ne changent pas. La matière ne leur importe pas, la forme seule les intéresse. (P.-I.49)
Écart par rapport à l’ontique. Le partage ontologie/ontique est ici désigné comme partage forme/matière.
On peut se demander pourquoi, dans les sciences physiques, la généralisation prend volontiers la forme mathématique. La raison est facile à voir ; ce n’est pas seulement parce que l’on a à exprimer des lois numériques ; c’est parce que le phénomène observable est dû à la superposition d’un grand nombre de phénomènes élémentaires tous semblables entre eux ; ainsi s’introduisent tout naturellement les équations différentielles. […] Les mathématiques nous apprennent en effet à combiner le semblable au semblable. […] C’est donc grâce à l’homogénéité approchée de la matière étudiée par les physiciens que la physique mathématique a pu naître. (P.-I.171)
Beaucoup de matière rassemblée exhausse l’homogène, le semblable des formes par-delà les différences d’étants…
L’esprit mathématique dédaigne la matière pour ne s’attacher qu’à la forme pure. C’est lui qui nous a enseigné à nommer du même nom des êtres qui ne diffèrent que par la matière, à nommer du même nom par exemple la multiplication des quaternions et celle des nombres entiers. (P.-II.106)
À nouveau sa manière (forme/matière) de pointer que la mathématique est l’ontologie
Weyl
L’applicabilité de notre science apparaît comme un symptôme de son enracinement. (W.-32)
Enracinement… dans l’Être !
Une pensée…
Weyl
La mathématique est la science de l’infini. Avoir rendu féconde, pour la connaissance de la réalité, la tension entre fini et infini est le grand accomplissement des Grecs. […] Pour les Grecs, la tension entre fini et infini et son dépassement deviennent […] le motif qui pousse la connaissance en avant. (W.-137) (W.-292)
Intéressante caractérisation des mathématiques qui complète bien celle de Szabo : ce qui fait la mathématique, ce n’est pas seulement la démonstration mais aussi la constitution d’une « tension entre fini et infini »…
Les mathématiques, a-t-on dit, sont la science de l’infini. En effet le mathématicien invente des constructions finies qui décident de questions par nature infinies. C’est son titre de gloire. (W.-267)
L’ontologie finie de l’Être infini…
On pourrait soutenir que les mathématiques s’occupent de choses qui ne concernent pas du tout l’homme. Elles ont la qualité inhumaine de la lumière stellaire, brillante, aiguë, mais froide. (W.-267)
Cf. Lautréamont…
Si les mathématiques, au nom de la sécurité, se retiraient sérieusement sur cette ligne de défense du simple jeu, elles se retrancheraient totalement de l’histoire universelle de l’esprit. (W.-305)
Les mathématiques ne sont pas un simple jeu sans enjeu.
Weyl défend les mathématiques dans le champ de la pensée, de l’esprit. C’est bien là un des enjeux de l’intellectualité mathématique.
De l’articulation entre mathématiques et physique mathématisée
Soit une caractérisation de la distinction mathématique/physique dans le lien même qui les unit et qui établit la physique mathématique (synthèse conjonctive ?)
Poincaré
Pour que la science soit possible… (P.-I.164) Les conditions qui ont permis le développement de la physique mathématique… (P.-I.167)
Réfléchir en mathématicien les conditions mathématiques de possibilité d’une physique mathématisée…
Le mathématicien ne doit pas être pour le physicien un simple fournisseur de formules ; il faut qu’il y ait entre eux une collaboration plus intime. La physique mathématique et l’analyse pure ne sont pas seulement des puissances limitrophes, entretenant des rapports de bon voisinage ; elles se pénètrent mutuellement et leur esprit est le même. (P.-II.104)
De l’articulation entre mathématiques et logique mathématique
Soit une caractérisation de la distinction mathématique/logique, là encore dans le lien qui les unit et qui établit la logique mathématisée.
Poincaré
La logique toute pure ne nous mènerait jamais qu’à des tautologies ; elle ne pourrait pas créer du nouveau ; ce n’est pas d’elle toute seule qu’aucune science peut sortir. […] Pour faire une science quelconque, il faut autre chose que la logique pure. Cette autre chose, nous n’avons pour la désigner d’autre mot que celui d’intuition. (P.-II.32)
Le logicien décompose pour ainsi dire chaque démonstration en un très grand nombre d’opérations élémentaires ; quand on aura examiné ces opérations les unes après les autres et qu’on aura constaté que chacune d’elles est correcte, croira-t-on avoir compris le véritable sens de la démonstration ? […] Évidemment non. (P.-II.36)
Cf. plus loin : le travail du mathématicien…
Cf. pour petit exemple de ce dont parle ici Poincaré une présentation logico-informaticienne du « théorème 2+2=4 » [9] qui mobilise plus de 2 000 sous-théorèmes pour retrouver le fondement des axiomes de la théorie des ensembles (en creusant à plus de 100 niveaux de profondeur)…
Weyl
Mathématique et logique doivent être formalisées conjointement. La logique mathématique si décriée dans le parti des philosophes a un rôle indispensable à cet égard. (W.-156)
La logique, en partage avec les philosophes… et avec les logiciens.
« Les mathématiques sont la science qui tire des conclusions nécessaires », cette définition proposée par Pierce en 1870 est restée en vogue pendant des décennies. Il me semble qu’elle ne fournit qu’une pauvre information sur la nature véritable des mathématiques. (W.-227)
Cf. la démonstration mathématique n’est pas une simple déduction logique… Ceci est bien illustré par son analogie avec le jeu d’échecs et la question singulière de comprendre une partie…
Noter aussi le non-besoin pour le mathématicien, même pensif, de définir les mathématiques, exactement comme c’est le cas en musique pour le musicien pensif.
Situation de la mathématique dans la pensée
Poincaré
Les mathématiques ont un triple but. Elles doivent fournir un instrument pour l'étude de la nature. Mais ce n'est pas tout : elles ont un but philosophique et, j'ose le dire, un but esthétique. Elles doivent aider le philosophe à approfondir les notions de nombre, d'espace et de temps. Et surtout leurs adeptes y trouvent des jouissances analogues à celles que donnent la peinture et la musique. Ils admirent la délicate harmonie des nombres et des formes ; ils s'émerveillent quand une découverte nouvelle leur ouvre une perspective inattendue ; et la joie qu'ils éprouvent ainsi n'a-t-elle pas le caractère esthétique, bien que les sens n'y prennent aucune part ? […] C’est pourquoi je n’hésite pas à dire que les mathématiques méritent d’être cultivées pour elles-mêmes. (P.-II.104)
Cf. plus loin : le triangle de l’intellectualité mathématique…
Distance prise avec une conception langagière de la pensée
Le constat que le mathématicien opère dans la distance entre pensée mathématique et mots (ou langage)
Rappel : ce point est développé de manière très intéressante dans le livre d’Hadamard…
Poincaré, plus intuitionniste peut-être que Weyl, n’insiste guère sur ce thème.
Weyl
Remarquer son insistance à détacher la pensée mathématique de la pensée langagière, lors même qu’il se déclare constructiviste.
Les mathématiques elles-mêmes n’ont pas besoin d’un langage quel qu’il soit, puisque ses formules ne signifient rien et ne véhiculent rien. (W.-169)
Les mathématiques sont célèbres pour l’air d’abstraction
raréfié qui y règne. Cette mauvaise réputation n’est méritée qu’à demi. Le fait
est que la première difficulté rencontrée par l’homme du commun quand on lui
enseigne à penser mathématiquement est qu’il doit apprendre à regarder les
choses en face beaucoup plus carrément ; sa confiance dans les mots
doit être ébranlée ; il lui faut apprendre à penser plus concrètement.
[…] Les mots sont des instruments dangereux. […] Nous assistons aux effets
désastreux du pouvoir magique des mots. […] Un scientifique doit percer le brouillard des mots
abstraits pour atteindre le roc concret de la réalité. […] On ne peut pas
appliquer les mathématiques tant que les mots obscurcissent la réalité.
(W.-214-5)
« Les mathématiques secouent les chaînes du langage. » Andreas Speiser [cité par Weyl] (W.-218)
Le jeu mathématique se joue sans bruit, sans mots, comme les échecs. Seules les règles ont à être communiquées verbalement, et il est naturel que toute argumentation sur les possibilités du jeu, par exemple sur sa consistance, se déroule dans le medium des mots et recoure à l’évidence. (W.-229)
Comparaison récurrente avec les échecs : comprendre une partie, ce n’est pas comprendre les règles !
La pensée des échecs est aussi hors langage, même s’il faut le langage pour apprendre les règles.
Subjectivité de mathématicien
À chaque fois, une subjectivité déclarée et assumée de mathématicien
Weyl
Les mathématiques, tel un arbre qui déploie librement sa cime dans les cieux, puisent leur force par mille racines dans une terre d’intuitions et de représentations réelles ; il serait désastreux de les tailler au nom d’un utilitarisme court de vue ou de les arracher du sol où elles ont jailli. (W.-32)
La subjectivité du mathématicien n’est pas utilitaire.
Si la mathématique veut rester un phénomène culturel qu’on puisse prendre au sérieux, elle doit rattacher un sens à ce jeu de formules. (W.-284)
La subjectivité du mathématicien n’est pas formelle mais attachée au sens mathématique.
Formaliser est la maladie des mathématiciens. (W.-126)
Cf. dans le débat de l’époque entre formalisme (Hilbert) et intuitionnisme (Brouwer), Weyl se situe du second côté.
Énoncé symptomatique de l’intellectualité mathématique car il vise à corriger, de l’intérieur, une dérive subjective des mathématiciens.
Nous, les mathématiciens, ne sommes pas un Ku Klux Klan avec un rituel secret de la pensée. (W.-212)
Subjectivité de mathématiciens, s’adressant à des non-mathématiciens…
Le travail du mathématicien
Poincaré
Le logicien décompose pour ainsi dire chaque démonstration en un très grand nombre d’opérations élémentaires ; quand on aura examiné ces opérations les unes après les autres et qu’on aura constaté que chacune d’elles est correcte, croira-t-on avoir compris le véritable sens de la démonstration ? […] Évidemment non. (P.-II.36)
Si vous assistez à une partie d’échecs, il ne vous suffira pas, pour comprendre la partie, de savoir les règles de la marche des pièces. […] Comprendre la partie c’est tout autre chose [que reconnaître que chaque coup a été joué conformément aux règles] ; c’est savoir pourquoi le joueur avance telle pièce plutôt que telle autre qu’il aurait pu mouvoir sans violer les règles du jeu. C’est apercevoir la raison intime qui fait de cette série de coups successifs une sorte de tout organisé. (P.-II.36)
Weyl procède au même type d’image…
Dans ce cadre subjectif, nécessité exhaussée d’une réflexion
Nécessité d’une intellectualité mathématique !
Poincaré
[Poincaré lutte contre « la philosophie anti-intellectualiste de M. Le Roy »] (P.-II.152)
Cf. conscience de l’anti-intellectualité…
Weyl
Que cette théorie [des ensembles] soit née des mathématiques a signifié seulement que l’Analyse est devenue abstraitement consciente de la méthode qu’elle pratiquait depuis longtemps. (W.-144)
La conscience de soi des mathématiques et pas seulement des mathématiciens
Nous sommes moins certains que jamais des fondements derniers (de la logique et) des mathématiques. Comme tout le monde et toute chose aujourd’hui, nous avons notre « crise ». Nous l’avons depuis bientôt cinquante ans [texte de 1946]. Apparemment cela ne semble pas gêner notre travail quotidien, et pourtant en ce qui me concerne, j’avoue que cela a exercé une influence considérable sur ma vie de mathématicien : j’ai orienté mes intérêts vers des champs que je considérais comme relativement « sûrs ». (W.-247)
L’intellectualité mathématique est liée au sentiment d’une crise des fondements…
« Pour un mathématicien professionnel, dont le travail consiste à faire quelque chose, non pas à parler sur ce que lui ou d’autres ont fait, c’est une expérience assez morose que se surprendre en train d’écrire sur les mathématiques. « (G. H. Hardy) […] Je ne partage pas le dédain de G. H. Hardy à l’égard de celui qui « parle sur » […] L’activité créative non contrôlée par la réflexion risque de se détacher de toute signification, de perdre contact et perspective, de dégénérer en routine. (W.-266)
Il y a bien deux niveaux : le discours mathématique et le discours du mathématicien pensif.
Le risque de l’activité créatrice, quand elle n’est pas surveillée par la réflexion, est qu’elle dévie du sens, se fourvoie, cristallise en routine – le risque de la réflexion, de dégénérer en un « parler sur » qui paralyse la puissance créatrice. Ce que nous avons fait ici, c’est de la réflexion. (W.-307)
Il faut une réflexion, et celle-ci génère son risque propre : devenir un « parler sur les mathématiques », un discours extérieur, une épistémologie !
Réflexion = activité du mathématicien pensif (réflexif) = intellectualité mathématique
La dimension esthétique dans les mathématiques et dans le travail du mathématicien
Un souci de réfléchir en mathématicien la dimension esthétique des mathématiques, d’exhausser la capacité du « beau mathématique » d’orienter le working mathematician (voir citations précédentes).
L’adresse aux non-mathématiciens
Un souci de s’adresser aux non-mathématiciens pour rendre compte des mathématiques.
La mathématique concerne la pensée de tout un chacun
Pourquoi tout un chacun est amené à rencontrer dans sa vie les mathématiques. Par exemple :
Weyl
Les mathématiques, en dépit de leur ancienneté, ne sont nullement vouées par leur complexité à une sclérose progressive ; elles sont bien vivantes, et se nourrissent par les racines profondes qu’elles plongent dans l’esprit et la nature. (W.-230)
Toujours cette défense des mathématiques auprès des non-mathématiciens…
Le contenu de pensée de tel concept mathématique
Si l’on recense ainsi la didactique conceptuelle à laquelle se livre Poincaré et Weyl, on a la liste des concepts ou catégories suivants :
· l’espace
Noter ici que la catégorie mathématique n’est pas le concept philosophique, en particulier l’a priori kantien. L’espace n’a nul rôle de « fondement » ou de « transcendantal » pour la pensée mathématique. Cf. le point suivant relevé par Weyl :
Le temps est antérieur logiquement à l’espace. (P.-II.98)
Si la réflexion mathématicienne se voulait philosophisante, elle devrait remonter à la question du temps sur laquelle la mathématique ne dit à peu près rien (cf. l’étude d’Albert Lautman sur le temps en mathématique)
· le continu
· le nombre
· la symétrie
· la grandeur (toujours mathématique, bien sûr)
· l’expérience (dans le champ propre des mathématiques)
· l’intuition
· l’axiomatique
· …
III. Plus synthétiquement…
Reprenons tout ceci plus synthétiquement.
Définition
On définira l’intellectualité mathématique comme une projection, en intériorité subjective, de la pensée mathématique dans la langue ordinaire, projection qu’on peut en effet appeler réflexion (au sens optique du terme).
Mathématicien pensif, ou réflexif
« En intériorité » ? Cf. subjectivité de mathématicien en acte, de working mathematician qui ne prend pas le discours mathématique comme objet extérieur. On peut penser ici à un ruban de Moebius : une seule face quoiqu’à tout moment il y a deux côtés du ruban. Soit la synthèse (connective ?) de 2 côtés en une seule face… L’intellectualité mathématique est donc l’affaire du mathématicien pensif, ou réflexif.
L’intellectualité mathématique n’est pas une affaire de « traduction »
La difficulté singulière tient à ce que la pensée mathématique n’est pas un langage (comme la musique, comme les échecs…).
D’où que la projection de cette pensée non langagière dans le langage courant ne soit pas une traduction ! Même chose en musique !
Différences mathématique/musique
Différences sciences/arts
Les rapports de l’intellectualité mathématique aux sciences (ou à La Science) divergent de ceux de l’intellectualité musicale aux autres arts (ou à l’Art) car
mathématique/Science≠musique/Art
En effet mathématique/Science = ontologie/ontique = Être/étants alors que musique/Art = écoute/sensible. Bref, la musique n’occupe pas une position centrale et névralgique dans le dispositif diversifié des arts (diversifié à mesure de la dispersion des 5 sens) comme la mathématique en occupe une dans les sciences (à mesure de sa position d’ontologie : cf. Badiou).
Différence de rapport à la philosophie
D’abord mathématiques/philosophie≠musique/philosophie, et ce de deux façons :
· {mathématiques→philosophie} ≠ {musique→philosophie} car si mathématiques et musique sont bien deux conditions pour la philosophie (Badiou), la mathématique étant l’ontologie, son conditionnement sur la philosophie est tout à fait singulier et prépondérant.
· {philosophie → mathématiques} ≠ { philosophie→ musique} : cette fois, c’est l’effet en retour qui est sensiblement différent. Ceci concerne les intellectualités plus que les disciplines proprement dites.
Je soutiens que la philosophie agit d’une triple manière sur l’intellectualité musicale :
— pour lui proposer d’abord une figure du temps pour la pensée, une figure de la contemporanéité (en ce point, la philosophie se présente pour l’intellectualité musicale comme une météorologie : elle indique le temps) ;
— pour l’aider ensuite à s’orienter dans la pensée (la philosophie intervient ici comme cartographie) ;
— enfin pour aider l’intellectualité musicale à penser pour son compte propre les conditions de possibilité de tel ou tel énoncé, de telle ou telle proposition (ici la philosophie s’avance comme géologie).
{Contemporanéité, orientation, conditions de possibilité} : ces trois aspects n’agissent par de même en direction de l’intellectualité mathématique.
Mon hypothèse est même que la philosophie n’apporte pas le même appui à l’intellectualité mathématique et que celle-ci, quand elle se réfère à la philosophie, a pour principal (ou premier objectif) de s’en désencombrer. Cf. écrits examinés : dégagement pragmatique (Poincaré avance régulièrement l’idée qu’il n’y a pas lieu de discuter de questions philosophiques et que le mathématicien les tranche en élisant la solution la plus « commode »…) plutôt que conditionnement en retour de la philosophie sur la mathématique et/ou l’intellectualité mathématique.
Il me semble donc que les effets intra-mathématiques de la philosophie, surtout de cette philosophie qui est étroitement conditionnée par la mathématique (Descartes, Leibniz, Husserl, Badiou) sont minimes, et même récusés par les intellectualités mathématiques examinées.
Il est vrai qu’on peut penser que l’intellectualité mathématique a eu à se déprendre de la philosophie positiviste, un peu comme l’intellectualité poétique a eu à le faire par rapport à la philosophie d’Heidegger qui lui assignait une place onto-logique éminente : celle de gardien de l’Être…
Je poserai volontiers : mathématique/positivisme=poésie/Heidegger (voir à ce titre le récent livre de Judith Balso sur Pessoa [10]).
Deux caractéristiques communes
Deux traits communs aux intellectualités mathématique et musicale :
La mathématique est la cible
Il y a intellectualité mathématique quand les flèches examinées (par exemple entre mathématique et physique) ont la mathématique pour cible, c’est-à-dire quand l’enjeu est fondamentalement celui des mathématiques, et ce même lorsque le discours s’adresse à des non-mathématiciens ou s’interroge sur la physique mathématisée. Même quand l’intellectualité mathématique se déploie sous la forme privilégiée d’une didactique, adressée donc à des gens de l’extérieur, il y a intellectualité mathématique (et pas seulement cours ou vulgarisation pour des profanes) lorsque ce travail est conçu du point de ses effets internes au travail du mathématicien, comme l’occasion d’une clarification, d’une mesure inhabituelle prise des rapports entre mathématiques et extérieur.
Le mathématicien est celui qui fait des mathématiques
Il y a intellectualité mathématique quand le mathématicien est saisi dans sa subordination aux mathématiques, comme celui qui fait des mathématiques. Quand il est question du mathématicien dans l’intellectualité mathématique, c’est donc au titre de sa fonction d’agent des mathématiques, d’acteur particulier, et non pas dans une introspection psychologisante ou dans une exaltation de son personnage.
Thèmes, enjeux, intensions
Recensons maintenant de quoi est fibré la matière même de l’intellectualité mathématique.
Je proposerai une triple détermination, analogue à celle de l’intellectualité musicale quoique sensiblement différente.
L’intellectualité mathématique travaille sur les trois dimensions suivantes :
Onto-théorie
Voir le statut ontologique qui dispose la mathématique au cœur de toute science (puisque l’être est commun à tous les étants). J’appellerai cela la dimension onto-théorique de l’intellectualité mathématique : il s’agit de réfléchir à quelles conditions la mathématique peut poursuivre son travail théorique en interne et en externe, en prenant la mesure de son statut de science particulière. Par exemple qu’est-ce qu’une théorie proprement mathématique de l’espace, à la fois comme théorie interne et en même temps comme susceptible ipso facto d’entrer en relation étroite avec la notion physique d’espace ?
Logique
Voir le statut mathématique de la logique : il s’agit cette fois pour l’intellectualité mathématique de prendre mesure du démêlé de la mathématique avec la logique, démêlé interne (puisque tout ceci se déploie à l’époque de la logique mathématisée) mais aussi externe s’il est vrai qu’il s’agit aussi toujours de trancher la non-fusion des mathématiques et de la logique et de travailler à l’ombre d’une logique qui rayonne bien au-delà des seules sciences ; c’est à ce niveau que le souci didactique est sans doute le plus prégnant.
Esthétique
Voir le statut mathématique de l’esthétique, c’est-à-dire le rôle joué par le beau dans les mathématiques – ce qui débouche aussitôt sur la question du sens, et aussi du sensible - ; c’est surtout à ce niveau que le rôle du mathématicien dans le « faire mathématique » est pris en compte.
Triple interlocution
Cette triple dimension s’articule à une triple interlocution privilégiée
1) celle avec les sciences pour l’onto-théorique ;
2) cella avec la philosophie pour la logique ;
3) celle avec les arts pour l’esthétique.
« Les mathématiques ont un triple but. Elles doivent fournir un instrument pour l'étude de la nature. Mais ce n'est pas tout : elles ont un but philosophique et, j'ose le dire, un but esthétique. Elles doivent aider le philosophe à approfondir les notions de nombre, d'espace et de temps. Et surtout leurs adeptes y trouvent des jouissances analogues à celles que donnent la peinture et la musique. Ils admirent la délicate harmonie des nombres et des formes ; ils s'émerveillent quand une découverte nouvelle leur ouvre une perspective inattendue ; et la joie qu'ils éprouvent ainsi n'a-t-elle pas le caractère esthétique, bien que les sens n'y prennent aucune part ? […] C’est pourquoi je n’hésite pas à dire que les mathématiques méritent d’être cultivées pour elles-mêmes. (Weyl, 104)
L’ensemble peut se figurer ainsi :
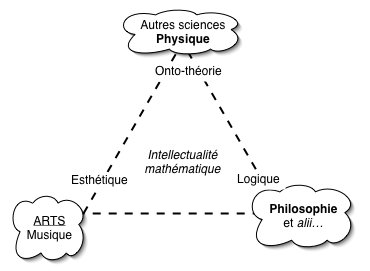
Je donne, par comparaison, l’espace de déploiement de l’intellectualité musicale :
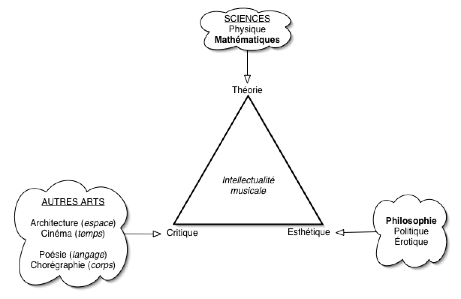
Différents types d’intellectualité mathématique ?
Pour l’intellectualité musicale, on peut distinguer 3(+1) types selon que l’accent principal est mis sur la théorie, sur la critique, sur l’esthétique ou qu’un équilibre général est préservé, ce qui pourra ainsi se figurer :
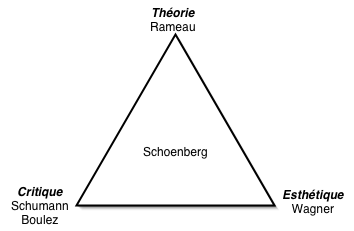
En est-il de même pour l’intellectualité mathématique ? Encore faudrait-il diversifier les intellectualités mathématiques prises en compte et mieux les analyser que je ne l’ai fait.
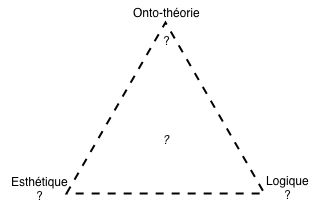
Il me semble que Poincaré est plus soucieux de didactique, quand Weyl est plus soucieux de faire prendre à la pensée mathématique ses distances d’avec le langage mais ceci ne suffit pas à les situer différemment dans mon repère à trois dimensions. Laissons donc cette question à d’autres.
L’anti-intellectualité mathématique
Il faut prendre acte de deux choses :
— la plupart des mathématiciens sont des working mathematicians qui n’éprouvent pas le besoin d’une intellectualité mathématique (on a le même phénomène en musique où la plupart des musiciens se vivent comme artisans) ; rien à redire à cette situation, bien sûr ;
— il existe par contre des musiciens et des mathématiciens qui combattent explicitement la voie de l’intellectualité ; en musique, la généalogie a pour colonne vertébrale la succession des noms suivants : Chopin-Debussy-Varèse-Berio. J’appelle cela une « anti-intellectualité musicale ». Or il existe de même une « anti-intellectualité mathématique » dont un nom ressort déjà des écrits de Weyl et qui est celui de G. H. Hardy. Il a écrit un livre qui n’est pas de mathématiques, mais qui est une biographie : L’apologie d’un mathématicien et celle-ci s’engage sous le signe suivant :
Ce livre, non de mathématiques mais « sur » les mathématiques est un aveu de faiblesse. J’écris sur les mathématiques parce que, comme tout mathématicien qui a dépassé la soixantaine, je n’ai plus la fraîcheur d’esprit, l’énergie ni la patience de poursuivre fructueusement ma propre tâche. (10)
Bref, pour Hardy, cette réflexion de vieux mathématicien devenu impuissant sur lui est faute de mieux…
Il faudrait recenser les figures plus constituées d’une anti-intellectualité mathématique : sont-elles à l’égal de ce qui se passe en musique ? Sans doute pas car l’intellectualité mathématique n’a pas la même histoire que l’intellectualité musicale.
Deux hypothèses
Terminons ce petit panorama par deux hypothèses.
Constitution de l’intellectualité mathématique dans la seconde partie du 19° siècle
La première est sur le moment de constitution de l’intellectualité mathématique proprement dit (j’ai avancé la date précise de 1750 pour l’intellectualité musicale, date qui distingue le premier du second Rameau).
Il me semble qu’en matière d’intellectualité mathématique il faudrait la chercher dans la seconde moitié du XIX° siècle, quand la mathématique va engager un double bouleversement :
1) de la géométrie et donc du concept mathématique d’espace ;
2) de la logique via sa mathématisation.
Il semblerait que ce soit ce double ébranlement qui suscite la nécessité chez les mathématiciens, et pas les moins brillants ni les moins productifs, de réfléchir leur science et qui éveille donc la figure du mathématicien pensif.
Je laisse en tous les cas cette hypothèse à la perspicacité de mon auditoire.
Aujourd’hui ?
Qu’en est-il de notre « aujourd’hui » ? Mon hypothèse est ici qu’une nouvelle configuration est peut-être en train de se dessiner.
Trois traits à ce titre, liés à chacune dans trois disciplines concernées :
1) dans les mathématiques, il n’y a pas seulement le renouveau manifeste des théories mathématiques pour la musique (voir les travaux de Guerino Mazzola) mais surtout un nouveau souci, me semble-t-il, d’intellectualité mathématique dont, en un sens, le récent colloque Cerisy sur la logique m’a convaincu ;
2) dans la philosophie, il est manifeste que l’époque n’est plus à la méditation interminable sur sa fin : de nouvelles perspectives viennent relever la métaphysique, à la fois contre le thème de la fin de la philosophie mais aussi contre le néo-kantisme et à l’écart d’un certain heidegerrianisme. À mes yeux, la philosophie de Badiou en est l’exemple le plus ample et le plus susceptible de nous intéresser pour une double raison :
— d’abord il s’agit d’une philosophie explicitement conditionnée par la mathématique en même temps que libérée des tâches ontologiques que cette dernière assure au mieux ;
— ensuite il s’agit d’une philosophie qui évalue la logique comme étant « en partage » puisqu’elle revendique une Grande Logique de statut explicitement philosophique.
3) dans la musique enfin, la nouveauté me semble que l’intellectualité musicale désormais est nommée et par là plus explicitement formulée et formulable.
On entre peut-être ainsi dans une seconde étape de l’intellectualité musicale marquée par l’identification réflexive de sa spécificité.
À ces trois titres au moins, notre aujourd’hui me semble celui d’une possible « nouvelle alliance » entre musique, mathématiques et philosophie, singulièrement via la nouvelle alliance des intellectualités musicale et mathématique.
Telle est, ultimement, la raison légitimant cet exposé.
–––––
Questions,
objections et réponses
[Je résume la discussion qui a suivi l’exposé (en séance et hors séance) par le petit jeu suivant de questions-objections/réponses]
Est-il bien légitime de situer les mathématiques « au centre » des sciences ?
Oui, à mesure du statut d’ontologie attribué aux mathématiques (l’ontologie étant « au centre » des différentes ontiques).
Ceci consonne d’ailleurs avec la transformation du concept de science (à partir de Galilée) qui a conduit la modernité (celle du « sujet de la science », au sens de Lacan) à tenir qu’une science, pour être telle, devait désormais être mathématisable (ou se penser « à la lettre »).
Il y a bien sûr des rapports directs entre autres sciences (entre « ontiques » : par exemple entre physique et biologie - cela indique alors que tout étant vivant est aussi fait de matière inerte) mais ces rapports ne raturent pas le caractère tout à fait singulier des relations entre mathématiques et autres sciences.
À l’inverse, le caractère « central » des mathématiques ne rature pas l’existence d’influences réciproques de ces sciences (par exemple de la physique) sur la mathématique (Poincaré y insiste d’ailleurs).
À parler de « mathématiciens pensifs », ne risque-t-on pas de laisser entendre que le working mathematician, lui, ne penserait pas ?
Non ! Bien sûr, les mathématiques, comme les autres sciences, pensent, et donc le working mathematician pense quand il fait des mathématiques.
L’adjectif « pensif » (et non le substantif « penseur » !), au demeurant emprunté à Victor Hugo qui en fait grand usage, veut désigner quelque chose de plus singulier qu’une pensée mathématique : très exactement une réflexion mathématicienne sur cette pensée mathématique.
Puisqu’on retrouve également une délimitation par rapport à la métaphysique de l’intérieur même de la philosophie, en quoi s’agit-il bien, dans le cas de Poincaré et Weyl, d’une délimitation mathématicienne ?
Il est vrai qu’un rejet de la métaphysique existe de l’intérieur même du champ philosophique (songeons par exemple à Heidegger). Mais alors le mot « métaphysique » opère tout autrement qu’il ne le fait dans le discours de Poincaré et Weyl : pour Heidegger par exemple, la critique de la métaphysique (et de l’ontothéologie) légitime un retour à une ontologie native, présocratique, étroitement imbriquée au poème. Elle opère donc comme appel à revenir à une philosophie véritable (au sens d’Heidegger).
Pour Poincaré et Weyl, le même mot « métaphysique » désigne tout autre chose : précisément un espace de pensée radicalement étranger à l’espace scientifique et mathématique, et dans lequel les mathématiciens n’ont pas à se compromettre. Cet espace « métaphysique », fait des concepts de « cause », de « liberté », d’« essence » et d’ « existence », de rapport entre « intelligible et sensible », de « nature de la vérité », de « dualisme objet/sujet », etc. désigne alors bien la philosophie en son noyau de pensée propre.
Pourquoi ne pas compter dans l’intellectualité mathématique les théories mathématiques de la musique, en particulier celle de Mazzola ?
Théoriser mathématiquement la musique, c’est tout simplement une manière particulière de faire des mathématiques. Or l’intellectualité mathématique n’est pas un « faire (de) la mathématique » mais un « la réfléchir » en projetant la pensée à l’œuvre dans le faire dans la langue vernaculaire.
Compter la théorisation mathématique de la musique (comme de la physique ou de l’économie) dans l’intellectualité mathématique reviendrait purement et simplement à ne pas distinguer ce qu’il s’agit précisément de discerner.
L’intellectualité mathématique n’est-elle pas une pratique spontanée de tout mathématicien, même s’il ne prend pas le soin de la formuler par écrit ?
Oui par un côté, car cette réflexion mathématicienne sur la pensée mathématique est bien sûr partageable par tout mathématicien. Non cependant, car la catégorie d’intellectualité mathématique vise à cerner des pratiques singulières du mathématicien (pensif) : celle consistant à donner forme transmissible, publique à cette réflexion, que ce soit par écrit (cas le plus manifeste) ou par oral.
On précisera donc, utilement, que l’intellectualité mathématique va de pair avec le souci de transmettre cette réflexion mathématicienne, ce qui implique l’étape (la pratique particulière) de fixer la projection faite dans la langue, de lui donner forme singulière.
L’intellectualité mathématique ne se loge-t-elle pas également dans les marges ou les interstices des articles mathématiques proprement dits ?
En effet, un article mathématique somme toute s’écrit aussi avec des mots (à la différence de la musique qui n’y recoure, dans une partition, que marginalement). On peut donc penser qu’un volet particulier de l’intellectualité mathématique se jouerait dans des parties singulières des textes mathématiques ordinaires et pas uniquement dans des textes spécifiques (quand il n’y aurait aucun sens à rechercher de l’intellectualité musicale dans des partitions !).
Ceci pourrait contribuer en effet à distinguer différents types d’intellectualité mathématique.
Dieudonné ne serait-il pas un exemple d’anti-intellectualité mathématique ?
Si c’est à raison de sa critique de « l’épistémologie »
ou d’une supposée « philosophie des mathématiques », non : tout
au contraire, j’ai tendance à trouver que ses résumés en tête de chapitres de ses
Éléments d’analyse fourniraient un bon exemple de cette intellectualité
mathématique se logeant dans les marges ou interstices des textes
mathématiques. Et son Abrégé d’histoire des mathématiques constitue également un exemple assez rare d’histoire
mathématicienne de sa discipline.
Pour dégager d’autres formes d’intellectualité mathématique, ne faudrait-il pas examiner plus attentivement ce qu’il en est des écrits de vulgarisation mathématique ?
En effet.
Je rechigne à compter la vulgarisation mathématique ou
scientifique en général dans l’intellectualité mathématique car il y s’agit le
plus souvent soit d’épistémologie grossière, soit de mathématiques saisies comme
curiosité plutôt que comme pensée. Mais il est vrai qu’il faudrait aller y voir
de plus près et que certains de ces travaux relèvent peut-être d’une véritable intellectualité
mathématique : pour donner une comparaison en musique, l’ancienne
collection Solfège du Seuil, consacrée à
la vulgarisation musicale des œuvres des grands compositeurs, ne relève guère
de l’intellectualité musicale sauf en quelques ouvrages, en général écrit d’ailleurs
par des compositeurs, comme ceux de Boucourechliev consacrés à Schumann et
Beethoven, ou celui de Barraqué consacré à Debussy…
N’est-il pas trop étroit d’établir l’existence d’une intellectualité mathématique sur la seule base de Poincaré et Weyl ?
Oui. J’ai bien conscience de travailler ici sur une base très restreinte. Ceci dit l’intellectualité mathématique n’est nullement une nouvelle « discipline » au sens universitaire du terme, qui serait donc dotée de continuité, de permanence, de protocoles stables, etc. L’intellectualité mathématique est une pratique discontinue, à chaque fois singulière (comme l’est au demeurant l’intellectualité musicale, qui se constitue en contraposition manifeste à la discipline musicologique). Donc deux singularités constituent déjà des repères significatifs. Mais il va de soi que l’hypothèse de l’intellectualité mathématique suppose, pour être durablement tenable, l’existence d’autres singularités que les deux aujourd’hui exhaussées.
Peut-être doit-on déjà y ajouter la figure de Dieudonné, et sans doute celle de Grothendieck (à moins qu’il ne faille plutôt décompter ce dernier dans la catégorie des mathématiciens ayant également fait œuvre philosophique).
Pourquoi une naissance si tardive, seulement dans la seconde moitié du 19° siècle ?
J’ai donné deux raisons : le bouleversement de notions mathématiquement aussi essentielles que celles d’espace et de logique (rappelons que pour Kant, la logique était, depuis Aristote, devenue définitivement immuable).
Mais il est vrai qu’il y eut avant cela d’autres bouleversements mathématiques, non moins considérables, ne serait-ce que la question des infinitésimaux au XVIII° siècle et que celle-ci n’a apparemment aps donné lieu à la constitution d’une intellectualité mathématique.
Tout ceci mériterait en effet d’être mathématiquement creusé, et tel n’est pas mon projet : j’ai assez à faire, pour mon propre compte, avec l’intellectualité musicale !
Si l’intellectualité musicale n’est née qu’autour de 1750, c’est parce qu’un faisceau de raisons convergeaient au mitan du 18ème siècle : la constitution de la musique en monde (le « monde-Musique ») sur la base d’un solfège inventé à partir du 9ème siècle mais abouti à partir du 14ème, la transformation sur cette base du régime des antiques consonances (primauté de la tierce sur la quarte qui fut pour Descartes « l’évènement » musical mettant en branle sa philosophie), la transformation de la science et donc de ce que théoriser veut dire (dont Rameau s’est emparé dans un premier temps), et – last but not least – la fin du baroque et du contrepoint laissant la place à un nouveau régime de « logique musicale » (la monodie harmonisée) et suscitant le débat esthétique dans lequel Rameau s’est jeté (la Querelle des Bouffons). Or il y eut constitution véritable d’une intellectualité musicale (et pas seulement d’une nouvelle théorie musicienne de la musique) quand le souci théorique s’est noué à un souci musicien de nature plus proprement « esthétique ».
Cet ensemble de conditions musicales si singulières a-t-il quelque équivalent en mathématiques dans la seconde partie du 19ème siècle ???
Ne faut-il pas tenir que dans le cas Leibniz (philosophe et grand mathématicien), il y a interaction entre philosophie et mathématiques et non pas développement parallèle ?
Oui, et pas seulement dans son cas. Le fait de distinguer, de séparer, n’implique nullement (tout au contraire) une négation des rapports entre les deux composantes ainsi écartées. Il devient au contraire plus simple de penser les rapports entre A et B une fois que A et B ont été clairement dissociés (distinguer la continuité et la dérivabilité permet ainsi de mieux penser comment l’une est liée/déliée à l’autre).
L’idée est cependant de clairement distinguer une philosophie conditionnée par la mathématique (Leibniz) et éventuellement une mathématique stimulée par un débat philosophique (Leibniz ?) d’une intellectualité mathématique proprement dite.
Toute intellectualité musicale ou mathématique n’a-t-elle pour motivation immédiate une défense ?
Oui, en première approche.
Cependant plus profondément, il s’agit surtout à chaque fois de défendre une nouveauté, une création de pensée et non pas un simple état des choses ; il s’agit de défendre précisément une percée possible qui se trouve menacée, en risquant d’être ensevelie sous la simple continuation académique ou sous la tyrannie de l’actualité renouvelée.
Schumann, Wagner, Schoenberg et Boulez ont clairement défendu la possibilité et la nécessité d’une nouveau type de pensée musicale.
Rameau est intervenu sur une position apparemment plus conservatrice (préserver les acquis du baroque à l’époque où celui-ci était dépassé par le nouveau style italianisant) mais il s’agissait en fait pour lui de déployer une nouvelle puissance musicale (l’articulation de sa nouvelle pensée harmonique à une conception de l’opéra et du drame), non pas de maintenir académiquement les savoirs répertoriés et sédimentés.
–––––