
Musique, mathématiques
et philosophie
Samedi 13 janvier 2001
Tom JOHNSON (compositeur) : Objets (mathématiques) trouvés
Un objet trouvé, une chose qu'on prend comme elle est. Pas d'art, pas de technique, pas de fiction. Essayer d'être modeste et honnête, comme Marcel Duchamps. Accepter ce qu'on trouve, comme John Cage a accepté les choix des dés.
Bien. C'est simple. Mais si l'objet trouvé est un objet mathématique....
Found Mathematical Objects
Tom Johnson
The idea is simple. Find an object, any object, declare it a work of art, and it is a work of art. Art becomes truly objective, just an object, artistic techniques become unnecessary, and the seeds of "non-intentional" art are planted at the same time. This Marcel Duchamp principle, the "readymade" or the "objet trouvé," is now recognized everywhere as a perfectly valid way of making art. A generation of Fluxus artists developed this point of view, John Cage adapted it to compose music through chance operations, and it is now quite natural that a composer or artist might choose to work with a found mathematical object, like Pascal's triangle or the Narayana series or some automaton, just as well as with a urinal, a bicycle wheel, a comb, or a bottle rack. But before I explain my own way of using mathematical objects to construct musical compositions, let me to lay the esthetic foundations a little more solidly.
Philosophical considerations
In the very first seminar in this series, François Nicolas devoted quite a bit of time to discussing music as number and note, something algebraically definable. Here are a few phrases that I noted that morning:
This last phrase is actually a quotation of Pythagoras, but Nicolas referred to it in his lecture, as he did in his article Nombre, note et oeuvre musicales, where he also cites J.-J. Rousseau and Schoenberg and develops at some length the algebraic nature of music. Considering music as essentially symbols of numbers and notes can be regarded as neo-Platonist, but it is also very applicable today. Certainly my music, and the musical theory of my book Self-Similar Melodies, represents this point of view.
It seems clear to me, and I think François Nicolas would agree, that not all music today is coded in letters like "a, b, c" and measured in time with precise algebraic symbols like quarter notes and half notes. I am particularly reminded of Gerard Grisey when I think of non-algebraic music. Grisey once wrote about how he had discovered as a young composer that "music is not about notes, it is about sound." The importance of this point of view for this composer will be clear to anyone who knows Grisey's music, but the comment was so foreign to my own way of thinking that I wrote him a letter. "No," I said, if I remember my letter correctly, "only notes are real. Sounds are phenomena that can not be measured accurately with all the tools in IRCAM. Each one of us perceives them quite differently, they change with every acoustical space, and they can only be written very approximately with words like mezzo piano and bowed cymbal. Notes, on the other hand, truly exist, with precise definitions. If I write "c-sharp, quarter note," there is no ambiguity, and if I write a melody, this is a real musical entity, valid for any tempo, any instrument. Sounds on the other hand are just vague approximations of indefinable ideas."
Grisey was perhaps offended by my letter, which challenged his esthetics, but he later recognized the validity of my point of view, and I of course came to respect his as well, particularly after I heard the Chansons pour traverser le seuil performed by Klangforum Wien. I remember a friendly chance meeting toward the end of Grisey's life, when he acknowledged that music could also be about notes, and I acknowledged that it was also about sound. It was obvious that Grisey needed to write notes if he expected people to play his music, and I needed sound if I expected people to hear my music, but we remained faithful to our philosophical preferences: sound for him, notes for me.
Another philosophical point is more complicated, because it touches on ideal reality, which touches on religion. If number existed before music, perhaps before anything, then mathematical concepts are eternal, and music that comes from numbers is somehow connected with the infinite. Quoting François Nicolas again, "L'oeuvre est une modalité particulière de croisement entre fini et infini, croisement dont il existe bien un modèle en pensée dans la problématique de l'incarnation chrétienne." The text Nombre, note et oeuvre musicales continues with a dizzying number of considerations about all the senses in which number and music are finite and infinite, and what constitutes a completed work, an open work, a finite work, and so on. Like most philosophical problems, if one examines them carefully, they become enormously complicated, and never lead to simple conclusions. The important thing for us here is simply to recognize that the question is valid. Works that come directly from number do become the incarnation of some kind of nature in some way.
I was reminded of all this again recently when I heard an interview with an artist who paints icons in the Greek Orthodox tradition. The esthetic she described has little to do with religious painting in France or Italy, and little to do with any common esthetics I know, but as one who composes with "found mathematical objects," I could identify with certain things she was saying:
It is this last point that particularly reminds me of my own work. When I listen to a sequence determined by an automaton, for example, I have the feeling that the music is totally self-contained and has no need for listeners. I would not say that I write sacred music, at least not in any of the pieces I will discuss here, and yet, a mathematical object, which has existed for many years or centuries, and which may even have existed before any humans suspected its existence, does have an absolute quality. It is not just the expression of a composer's wishes. If John Cage talked about non-intentionality, and my teacher Morton Feldman said over and over, "Let the music do what it wants to do," my use of mathematical objects is clearly a continuation of this search for objective music. Like my closest musical ancestors, Cage and Feldman, I look, in my own way, for music that comes from outside myself, not music that arrives subjectively from personal ideas and feelings.
From mathematical object to musical object
Three types of automata
How can a composer take a "readymade" mathematical object and code it into an artistic object as Duchamp would have done, without altering or decorating it, without using traditional composing techniques?
François Nicolas is right when he observes that one does not normally find a direct relationship between mathematics and music the way one finds relationships between mathematical formulas and physical phenomena, but one can make a direct relationship if one wishes to. As an example, let me begin with a simple infinite automaton:
n-> n, n+1, n
If we begin with 0, this leads to 010, the second letter leads to 121, and the process creates a "fixed point sequence":
01012101012123212101012101012123212123234323212123...
A mathematical object is clearly defined, and this is all a mathematician needs to know in order to go wherever he or she wants to go, but if we really want to see what is happening, it is better to spell out the progression in this way:
0
010
010121010
010121010121232121010121010
Now one can see how the sequence multiplies itself by three at each step, but the structure is much clearer if we go to a regular-spaced courier typeface and write:
0
010
010 121 010
010 121 010 121 232 121 010 121 010
and it can be even more clear if we write it as music, with 0=C, 1=D, 2=E, etc. :

and let me take that just one step further, as I did when I wrote Rational Melody No. 14 (1981):

The most important change here is that the numbers greater than zero now each have two musical codings. The letter 1 is coded as D when it occurs as 0 1 0, and G when it occurs as 1 2 1, and the subsequent numbers are each coded in two different ways as well. I didn't really think about this when I wrote the piece, and I was probably just following my traditional classical European training. To my ear the 1 was simply a neighbor tone, a decoration, when it came between two zeros, but when the music was ready to move, and it became the beginning of a three-note group, it had to become something else. Now several types of rests have been inserted as well, with short ones after every three notes, longer ones after every 9 notes, even longer ones after every 27 notes, and so on. This separates the levels for the ear, just as spacing separated the levels for the eye, when we were just looking at digits.
It may seem that I am now far away from the simple rule n -> n, n+1, n, but at every step the goal has been not to decorate or to depart from the basic rule, but rather to show the structure of the basic rule, to enter into this mathematical object, to be able to see and hear it as well as we possibly can. One can say that I am making subjective musical choices here as I select intervals and measure the lengths of the punctuations/rests, but behind these choices is a consistent desire to make the mathematics more clearly audible, not to mystify, not to transform the mathematics into something esthetic. I should point out that Duchamp also touched his objets trouvés ever so slightly. He gave a title to the urinal, calling it The Fountain, and signed it with the pseudonymn R. Mutt. He also placed the bicycle wheel on a little white stool/pedastal, just to cite a couple of examples.
Another infinite automaton was used to generate the music of Narayana's Cows. I will only explain this briefly, as this is one of my most frequently performed pieces, and was also the subject of a paper written in collaboration with Jean-Paul Allouche for the Journées d'informatique musicale (JIM) a few years ago. The Narayana sequence comes from a 14th-century Indian mathematician who posed this problem: If a cow bears a calf at the beginning of each year, and if each calf becomes a mother at the beginning of her fourth year, and if they all continue to give birth once a year, how many cows and calves will we have after x years?
The sequence is a sort of delayed Fibonacci series. Instead of the total for the year n being the sum of the years n-1 and n-2, we have to add the year n-1 plus the year n-3.
The sequence goes like this,
1, 1(1+0), 1(1+0), 2(1+1), 3(1+2), 4(1+3), 6(2+4), 9(3+6), 13(4+9), 19(6+13)...
and the music plays every cow literally year by year. The mothers are quarter notes, the daughters are eighth notes, and each generation is represented by a new and lower note of the scale.
Other automata can be found in my music, notably in the 18 movements of Automatic Music for Six Percussion (1997). These pieces also work with processes that can generate music endlessly, but they are considered "finite automata," becausse they only employ three letters : 1 (low note), 2 (high note), and 3 (rest). I won't explain further here though, as Automatic Music is the subject of another JIM article.
Three Transformations of Pascal's Triangle
Let's examine a piece that transforms a mathematical object into music in a very different way: The Chord Catalogue. Again the musical idea is simple: to play on a keyboard all the chords possible in one octave. There are 13 keys in a complete octave, and in any given chord, each key is either played or not played, so there are 2**13 = 8192 combinations in all, but that includes the empty set, which is not a chord, and 13 single notes, which are also not chords, so we have to subtract 14, giving a total of 8178.
Here we have a neat finite set of combinations, rather than a messy infinite sequence like those produced by the automata, so we have no problem of when to begin and when to stop and why. The problem is how to order the 8178 chords, but even that is not very difficult, because only a few possibilities are logical enough to remember and play. Either one starts with all the low possibilities and works through to the high ones, or vice versa, or one starts with the two-note chords and works up to 12-note and 13-note chords, or vice versa. I decided to start with the two-note chords, which were easy to play, then I learned how to play the three-note chords and four-note chords, gradually moving up until, after a few months of daily work, I began to be able to play the whole collection. It seemed obvious that this would also be the most natural sequence for the listener.
In the table below you can see how the chords fall into groups. The first line represents the 78 two-note chords and the last line represents the single 13-note chord. You will notice that this table is really Pascal's triangle lying on its side, with the empty set and the single notes missing.
- 1 3 6 10 15 21 28 36 45 55 66
- 1 4 10 20 35 56 84 120 165 220
- 1 5 15 35 70 126 210 330 495
- 1 6 21 56 126 252 462 792
- 1 7 28 84 210 462 924
- 1 8 36 120 330 792
- 1 9 45 165 495 1 10 55 220 1 11 66
- 1 12
- 1
I sometimes feel that The Chord Catalogue is the purest example of music that I found, rather than music I composed. I call it a composition by Tom Johnson, because I feel I have to take responsibility for what I have done, but at the same time, the piece seems a little like those Greek Orthodox icons, something that shouldn't be signed, something that was not truly the creation of an artist, but rather the incarnation of something else.
Pascal's triangle turned up again a few years later in one of the movements of Music for 88. Here the idea was to play all the chords that could be formed with only two intervals, the major second and the minor third. In the following fragment, which is the beginning of the piece called "Pascal's Triangle," one sees three lines of Pascal's triangle, symbolized by the two possible two-note chords, the four possible three-note chords, and the eight possible four-note chords:

A third piece transforms Pascal's rich mathematical model into very fast synthesizer music that pings away on a 7-note scale. The piece, called Triangle de Pascal Modulo Seven, became an Atelier de création radiophonique on France Culture, with some quotes and discussion at the same time. The two-hour broadcast took the music out to line 343, which is 343 notes long, but I will show only the beginning here. Note how the sequence reaches 1-6-1-6 cadences with lines 7, 14, and 21, and begins again with mostly zeros in the lines 7n + 1. The progression moves toward infinity with a remarkably clear self-similar structure that one probably hears even better than one sees:
The fact that three such different pieces could all be derived from Pascal's triangle is perhaps not surprising, when one considers that just within mathematics, this particular mathematical object has applications in algebra, fractals, combinations, probability theory, and many other areas. It won't surprise me if other composers also find additional and very different musical applications.
Self-Replicating Loops and Rhythmic Canons
Three older examples
This second part of this lecture is devoted to what I call "melodic loops," and what mathematicians generally think of as "cyclic groups." These are somewhat more sophisticated than the mathematical objects I have been discussing so far, and in fact, some questions have come up recently that are challenging even for good mathematicians like Thomas Noll and Markus Reineke, who have been helping me enormously lately. But I had best begin by going back to 1981, when I wrote Rational Melody No. 15, which is the first "self-replicating melody" and to 1991, when Dan Tudor Vuza published his analysis of "rhythmic canons" in Perspectives of New Music. These two starting points seemed for a long time to be completely different phenomena, though the more we study them, the more it seems that they are somehow two aspects of the same thing.
I won't go into detail about how you write a self-replicating melody, as you can find simple explanations in the lecture I gave in the JIM 1999, or in Self-Similar Melodies, and a more sophisticated explanation in the Leonardo Music Journal. I'll just say that to write Rational Melody 15 I constructed, with some help from David Feldman, a 15-note loop in such a way that a person playing only the first, third, fifth, seventh, etc. notes will be playing the same melody as the person playing all the notes. In my terminology, the melody "self-replicates," or makes a copy of itself, at the ratio of 2:1.
By contrast, a rhythmic canon, such as those studied by Vuza, is not concerned with pitches. It is just a question of breaking a loop up into segments that are exactly the same. We just want to find a rhythm which, when repeated in canon, fills every point on the loop. As an example I'll tell you about a piece I wrote in the spring of 2000, when I had an invitation to write music for a new instrument designed by Martin Riches that employed eight tubular bells. To begin I posed this question: What eight-note rhythm might fill a 24-note loop as three voices of a canon? I found 27 solutions, and selected the following one, which has an appealing waltz rhythm. Note that it is a palindrome, as are most of the other solutions:
X O O O X X X O O X X X O O O X
The voices of this rhythmic canon can be written on a single staff, since they all come at different times. The numbers indicate which voice is entering.

After the entrance of the first three voices, the 24-note cycle is already filled up, but the music goes to six voices, at which time there are two notes at each point. The notes could have been anything. I just selected these so as to have a nice arching melody. It also looked good, with the short tubes hanging in the center, and the long ones hanging at the sides.
On the surface, this rhythmic canon has little to do with the self-replicating melody we just saw, and yet both are cases of small loops fitting into large loops in particular ways. In Rational Melody No. 15, a 15-note loop was stretched out to become a 30-note loop, which contained two copies of the original 15-note loop. In the canon for Martin Riches, we divided a 24-note loop into three similar loops of eight notes. In terms of group theory, both pieces divide a cyclic group into similar sub-groups.
Loops for Orchestra, premiered at the Steirischer Herbst festival in September 1999, is another example of a mathematical object found in group theory that forms musical groups and sub-groups. In this case I was working with a 21-note cycle, or as a mathematician would say, I was in Z/21Z, where all numbers are read modulo 21. Below are the orbits one must follow if one wishes to have a 21-note loop that makes a copy of itself at a ratio of 2:1, the way Rational Melody 15 did, and I would say that this orbit structure is the essential mathematical object that generates the music. If you don't know what orbits are, the important thing is simply that if you want a loop 21 notes long to make a copy of itself at 2 :1, you have to make sure that all the notes falling into a single orbit are coded with the same musical letter. In this case there are six orbits, four of which I assigned to particular notes, and two of which I designated as silence.
Here are the 21 notes, numbered 0 to 20, and the basic melody, along with its half-time and quarter-time counterparts, all in unison.
The rests enabled me to have a second smaller loop turning in the holes of the larger one, once every seven sixteenth notes. This secondary loop could have been any length, but I chose a length of four. Four is prime with 21, so that the two loops cycle against one another, and short enough so that one can easily hear the turning. This second loop also self-replicates, but at 3:1:
Here is a detail from mm. 85 - 89, where one can see the 21-beat loop cycling in several different tempos, and the little four-beat loop falling in the holes.

The Loops for Orchestra is mostly about self-replicating and not about rhythmic canons, but I realized after writing the piece that it also contains rhythmic canons exactly like those defined by Vuza. Here is a detail from mm. 171-175, where the loop is heard on the beat in the oboes and violas, and off the beat in the horns, and these two sub-loops combine into one eighth-note loop, as heard in the second violin.
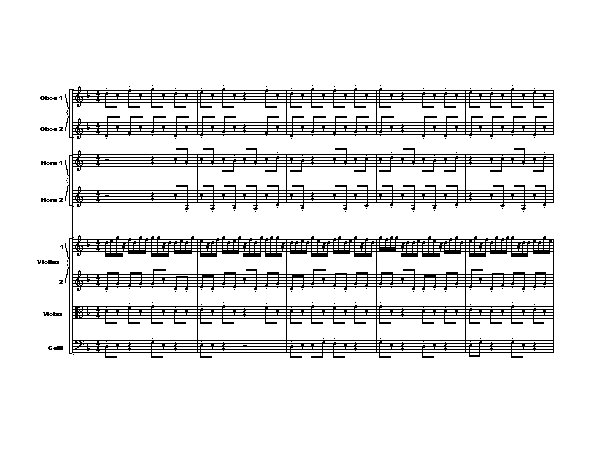
This 17-minute orchestra piece is not strictly deterministic the way the others we have seen are. In fact, in order to keep the music interesting and to hear all the kinds of heterophony I was finding in this remarkable 21-note loop, I had to do quite a bit of old-fashioned composing and orchestrating. It was even necessary to make some subjective decisions about how long something should last and how many times it should come back. I am happier when the mathematics takes care of all that. The result seems neater and cleaner, and I am "letting the music do what it wants to do," to quote Feldman again. Still, the constraints are very great if one always follows these two loops literally and keeps everything in exact unison, and I can imagine that another composer, working with the same loops and the same constraints, would end up with something quite similar.
Thomas Noll and polyrhythmic canons
No doubt the most important recent advances in all this have been the discoveries made in collaboration with Thomas Noll about how to make rhythmic canons with the voices moving at different tempos. Let me begin with this note from Paris to Berlin:
Below is my realization of this rhythmic canon. In order to cover all points of the total loop there are eight voices, three in the 3:1 tempo, and five in the 5:1 tempo. Again I notate the entire canon as a single melody, but here each individual voice plays the rhythm on its own repeated note.
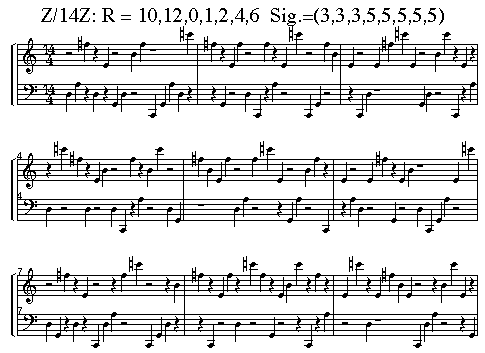
and here is the musical notation for the (0,1,2,4,5,8,9,11) canon that Noll suggests, with one voice at 1:1 and three voices at 3:1. This one makes a complete cycle in only three measures of 14/4 time.

Interlude for Guerino Mazzola
On November 6 Thomas Noll sent an email to me, and to several other colleagues, stimulating us with this challenge:
I don't remember what I sent, though I do remember that it wasn't very interesting musically - just something to show I could solve the problem. Recently, however, I came back to this period-16 proposition with somewhat more inspiration, and the result was like a fragment of jazz piano. It reminded me of our mutual friend Guerino Mazzola, who lectured in this series two months ago, and whose work has been influential for both Thomas and me. So I decided to add a short interlude for him here. At first there is just one voice, a fast one. Then I add the second fast voice, then the first slow voice, then the second slow voice, and finally two more slow voices, in order to fill out the complete 16-beat loop.

Markus Reineke and some theory
In October I received an email from Markus Reineke, a mathematician in Wuppertal, who had seen my article Self-Replicating Melodies. Though normally concentrating on abstract algebra, my article had turned his thoughts to music and orbits, and he had found some information he thought I'd like to have. He wrote:
I was pleased to know about this, as other mathematicians had not been able to tell me such things, and later Reineke sent me his complete list. It was good to know that he was interested in musical questions, and I wondered if he might have something to say about the more recent questions. I sent him a copy of Self-Similar Melodies, and enclosed some information about what Noll and I were currently finding, and this led to more communication from Reineke, which I think will be very useful, at least for me, once I have had time to digest it.
Let's go back to Noll's observation that a loop of 14 can be made with voices in two tempos (3:5). Noll defined the basic rhythm as (0,1,2,4,6,10,12), though I realized it above as (10,12,0,1,2,4,6), since it was more musical to leave the longest pause at the end of the phrase. The voices moving at 3:1 fall on (0,3,6,12,4,2,8) and those moving at 5:1 fall on (5,10,1,11,7,13,9), and Noll thought this was the only interesting solution, but Reineke found an additional one. Explaining this will be a bit technical, but it will only require one paragraph.
The man from Wuppertal, whom I have still not met, began with the observation that if a rhythm of seven notes fills out a 14-note loop with two voices having tempos of 3:5,
this is equivalent to saying that it is canonable at 1:5/3, which is to say it is canonable at 1:11, because
If x=5/3 mod 14
3x=5 mod 14
and x=11 (because 3*11=5 mod 14)
From here he went on to point out that one can have a "shift," which means that instead of simply multiplying the 14 numbers of this cyclic group by 11, we can multiply each by 11 and add 1, which gives a new orbit structure. Then he devised a system that uncovered eight different ways to make two-voice rhythmic canons at tempos of 3:5. Most of these ways are trivial, or simply transpositions of the one Noll found, but one is not: (0,1,2,3,5,6,11). Informed of this, Noll recognized his oversight, corrected it, and sent me a list of what he considers the essential seven-note rhythms that make canons in Z/14Z, along with the ratios possible for each:
Reineke also investigated two-voice rhythmic canons possible in loops of other lengths. Particularly interesting for me are the loops of 12 notes that make two-voice rhythmic canons at 5:1. His system shows that there are theoretically 72 ways to do this!
Of course, this particular discussion has to do with rhythmic canons, rather than self-replicating melodies, but Reineke too notes the similarity: "The calculation of orbits of course reminds one of the method for constructing self-replicating melodies with shifts. Is this just a coincidence or is it explainable mathematically? And is it a hint on how to compose a melody for the canonable rhythms?" There remain many other questions:
After compiling this list, and finding it already too long, Reineke wrote again, saying he is wondering whether a self-replicating loop, turning at 41,000 points per second, could also be useful for sound synthesis! But that is definitely too many unanswered questions for one lecture.
A complex example
In the last 20 or 30 years musicians often seem to assume that complexity is somehow better than simplicity, but I am always dubious. No one ever said Beethoven's music is better than Hummel's because it is more complex, and people who make computer programs and mathematical proofs know that the best, the most elegant solutions, are always the short simple ones that go directly to the essential points. So when I say that this final example is complex, I am not claiming that it is good or profound. On the contrary, piling up all these layers and tempos is probably quite simplistic, just something I did because I don't yet know how to put such things together elegantly. I saved it for last (1) because it is fascinating to try to listen to so much going on at once, (2) because it is rather amazing that such rational deduction could produce such a chaotic sounding result, and (3) because it seems to indicate just how little we really know about all this.
Let me tell you how it happened.
After Thomas Noll sent me his first findings about rhythmic canons that have sub-groups moving at different tempos, I was quite busy and content for several weeks simply working out cases where the voices were in ratios like 4:4:7, but early in December, I reminded him that I wanted to push the question further:
Finding a loop with a signature of three or more numbers prime to one another remains a top priority for me, Extremely rich musical possibilities here.
Thomas Noll didn't have an answer when the question had come up before, but this time he replied almost by return email:
That may require a bit of explanation. The basic rhythm (0,1,2,5,8) is multiplied by 2 in some voices, becoming (0,2,4,10,16) modulo 15, or (0,2,4,10,1). Other voices multiply the basic rhythm by 7, which gives (0,7,14,35,56) modulo 15 or (0,7,14,5,11), but we have to add 7 to each of those digits in order to get the 7:1 loop starting at the right point: 0+7=7, 7+7=14, 14+7=21 modulo 15=6, 5+7=12, 11+7=18 modulo 15 = 3, which explains the (7,14,6,12,3). The 11:1 loop is calculated by multiplying the basic rhythm by 11, and then adding 13, giving (13,9,5,8,11). That accounts for the three sub-groups in three different tempos with five notes in each sub-group, and all 15 points of the loop are now filled once and only once. But Noll continued in the same email with another example:
- (0,1,3,8) is canonable with period 16 and signature (3,5,7,11). These are two realizations:
- ((0,3,9,8),(2,7,1,10),(6,13,11,14),(4,15,5,12))
- ((0,3,9,8),(6,11,5,14),(10,1,15,2),(12,7,13,4))
This was a real shock for me. Four tempos at once! And two ways of doing it! I immediately began trying to write out the first solution as a FINALE program, which turned out to be a big job. In order to fill the loop of 16, I needed to multiply it into a loop of 16*3*5*7*11= 18,480 notes, or 1,155 measures of sixteenth notes in 4/4 time. To fill out this whole giant loop, the counterpoint has to consist of 26 voices, three voices moving at 3:1, and repeating 5*7*11 times, five voices moving at 5:1, and repeating 3*7*11 times, and so on. Here is the basic 1:1 loop, along with the multiples, and the numbers show you how the four multiples go together to use all16 available points:

I tried several different ways of ordering the mass of 26 voices before I found one, which I'm going to play for you, which seems more transparent than the others, but which is still pretty opaque. As I wrote recently in a letter to Reineke, "With 26 voices it's hard to hear much, but listening to it is kind of like looking at one of those Alhambra mosaics. You just sit there and think, 'how the hell could that be possible?'" Everything in my 26-voice canon is just that one basic rhythm, and everything in the Alhambra is just connecting points with a few rational angles, but these simplicities weave through one another in a great many ways.
This observation is reminiscent of the philosophical questions with which we began, and it will perhaps help to unify all this if I briefly go back to theory before we listen to this final example. I thought of the Alhambra parallel not only because I had a wonderful experience there a few years ago, but also because I attended an Arts and Mathematics colloquium in Maubeuge just last September. Particularly stimulating there was a lecture by Antonio Costa, a mathematician from Madrid, whose topic was "Islamic Art and Crystallographic Groups." Costa talked about how, for many centuries, mathematicians had tried to find all the ways in which regular polygons fit together, how they wanted to prove that only x ways could exist, and how this problem was never solved until Polya defined his 17 crystallographic groups early in this century. Costa told us about p6m and p3m1 and p4 and some of Polya's other groups, and for each one, he had an example from the Alhambra. Some mosaics had only one point of rotation and some had several. Some seemed to have mirrors that reflected them in three or four or five angles at once. All their symmetries could be seen quite clearly on a CD-ROM he had prepared.
What impressed me most was Costa's assertion that, while the Arabs wrote no treatises on any of this, all 17 crystallographic groups can be found in the Alhambra. Many artisans worked there in Granada over a period of several centuries, and they were quite devoted to tiling with polygons, not only because it was forbidden in Islam to represent human figures, but also because they believed the geometry they were finding was somehow sacred. God is everywhere. God is making this order, making this geometry, and finding it and looking at it will help to free us from our earthly ties. It was clear that they felt they were only finding these patterns, they would never have claimed to be creating them, and like the icon painter, they never signed their work either.
I certainly don't want to compare my 26-voice canon to the magnificence of the Alhambra, but maybe you too will find that the effect of the complexity is vaguely similar. Each of the 26 voices has its own pitch, and if you focus your attention on any single pitch, you can hear the four-note rhythm in one of the four tempos. Each of the four tempos is arranged symmetrically around a central D, and one can hear all four tempos on that central note. You will probably hear the rhythm more easily on some pitches than on other pitches, and the faster 3:1 voices are easier to hear than the slower 11:1 voices, and this synthesizer has its own particular sound, and each individual has greater or lesser capacity for particular kinds of pitch and rhythmic recognition, and your position in this room is another factor, but remember that all of this is only sound. The real music, that which lies behind the loudspeakers, is the notes!