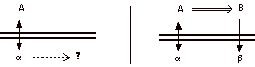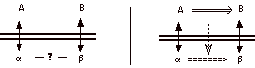Quand l’algèbre
mathématique aide à penser (et pas seulement à calculer)
la combinatoire musicale…
Samedi 15
février 2003, Ircam
(Séminaire Mamux)
François Nicolas
Je voudrais interroger les manières dont la
combinatoire musicale peut s’arrimer à l’algèbre
mathématique.
Toute une école de pensée, en particulier dans
les années cinquante du XXème siècle, a
proposé de prolonger le geste « sériel » de
Schoenberg en recourant à une algébrisation systématique
de la matière musicale. Les principaux noms de cette entreprise sont
bien connus : Milton Babbitt, Pierre Barbaud, Michel Philippot…
Cette orientation, transférant la charge des calculs musicaux à
la combinatoire mathématique, a connu un regain de jouvence avec le développement
de l’informatique musicale.
Si cette mathématisation de la combinatoire musicale
n’est pas sans mérite (j’en use en abondance), elle
n’est pas non plus sans péril : elle suggère
qu’une certaine rigueur algébrique pourrait être gage de
cohésion musicale, qu’une certaine cohérence des
déductions algébriques pourrait valoir pertinence pour un
développement musical. Où faire alors passer la frontière
entre un usage spécifiquement musical de cette algèbre et un
fétichisme des nombres, une servilité face aux
mathématiques ? La réponse ne va guère de soi :
certains soutiennent ainsi depuis longtemps que la musique, incapable de penser
entièrement par elle-même, serait intrinsèquement
subordonnée à la mathématique et devrait donc faire
ultimement valider ses idées par son tuteur mathématique. Deux
brèves citations pour exemplifier cette position :
· Thomas
d’Aquin d’abord : « La musique s’en remet aux
principes qui lui sont livrés par
l’arithmétique. »
· Leibniz
ensuite : « La musique est subalterne à
l’arithmétique »
Aujourd’hui que l’informatique musicale
multiplie les occasions de plier la musique aux lois de l’encodage et du
calcul numériques, il nous revient plus que jamais, à nous
musiciens, de tracer le fil d’une autonomie de pensée musicale qui
ne récuse cependant pas une alliance féconde avec la
pensée mathématique.
*
Pour traiter de cette voie en m’inscrivant dans le
thème obligé de cette journée, je partirai de quelques
remarques faites par Michel Philippot à l’occasion d’un
hommage rendu en 1976 à Milton Babbitt .
Philippot, s’en prenant à une
mécompréhension vulgaire de l’idée romantique
d’inspiration qui conduit à ce qu’il appelle « un
véritable nihilisme musical » ,
y propose de prendre appui sur ce que les mathématiques nous apprennent
en matière combinatoire.
Il relève ainsi l’intérêt de ce
qu’il nomme « les modèles mathématiques »
et dont il trouve l’archétype dans ce qui pour Milton Babbitt
constitue « un système musical » .
Si la création d’un système musical fait bien partie
intégrante de l’activité compositionnelle ,
le propre de Milton Babbitt — selon Michel Philippot —
serait de généraliser l’idée musicale de
série, non pas comme Boulez — c’est-à-dire en
étendant la combinatoire sérielle à tous les
paramètres du
son — mais en élargissant l’idée même de
série jusqu’à la notion de structure .
Philippot, explicitant ce qu’il entend par structure, décrit alors une structure algébrique
sur un ensemble mathématique et en vient ainsi à valider
l’hypothèse de Babbitt selon quoi la notion même de
composition musicale équivaudrait à celle de structuration
algébrique totale :
« l’idée de système musical est équivalente à celle de structure au sens mathématique du terme », écrit-il donc .
Ainsi « la conception d’une sérialisation
totale » viserait à généraliser les
systèmes mathématiques et conduirait par exemple à la
notion de structure de groupe .
Précisant qu’« à travers
l’histoire, les modèles mathématiques ont été
un puissant instrument pour développer l’imagination
musicale » ,
Philippot suggère cependant que cette équivalence entre musique
et mathématiques ne signifie pas identité mais vaut seulement
comparaison (« la transposition peut être comparée à l’opération
arithmétique d’addition » ).
Il précise cette autonomie relative en indiquant que si « une
telle structure de groupe garantit un niveau minimum d’organisation
musicale, cela cependant n’y suffit pas. En réalité la
structure [mathématique]
de groupe peut être comparée à une sorte d’enveloppe
dans laquelle des règles spécifique[ment musicales] de logique et de cohérence peuvent
être alors placées. » .
Philippot conclut alors sur cet énoncé : « la
cohérence d’un système musical donné est
proportionnelle à la quantité de ses contraintes mais
indépendante de leur nature. » .
Deux remarques sur ses propos.
1) Première remarque
S’il est vrai qu’on distingue la logique de la
mathématique par le fait que la première ne s’occupe que de
la forme des énoncés sans se soucier de l’existence
réelle des identités qu’ils convoquent, il faut alors tenir
que Philippot formule la thèse suivante : la logique musicale
trouverait sa formulation dans la mathématique.
Ou encore : si l’on peut distinguer formes
logiques de l’être et contenus d’être effectifs (ou existences réelles), alors
la mathématique constituerait à proprement parler la logique musicale —
je dis bien : la mathématique tout entière (donc
l’arithmétique, l’algèbre, la théorie des
groupes, etc.) et non pas la seule logique mathématisée —.
Cette thèse me semble éminemment
problématique. Ma conviction fondamentale est la suivante : la pertinence
des rapports mathématiques—musique n’a rien de
mystérieux si l’on veut bien admettre que les mathématiques
pensant l’être en tant qu’être, ce que les
mathématiques pensent vaut universellement pour tout être, pour
toute forme d’être et donc en particulier pour les êtres
musicaux : dit grossièrement le fait que 2+5=5+2=7 vaut aussi bien
pour des notes et des croches que pour des voitures ou des galaxies. Ceci se
dit plus subtilement — dans un langage philosophique —
ainsi : les mathématiques étant l’ontologie ,
elles valent pour tout étant.
Il n’y a donc pas lieu à mon sens de
s’étonner d’une certaine mathématisation de la
musique, ni de s’en offusquer. Le point que je veux aujourd’hui
réfléchir tient plutôt au statut donné par les
musiciens à cette application des
mathématiques à la musique (à cette application de
l’être en tant qu’être à l’être en
tant qu’étant musical) : la manière dont ceci est
réfléchi, thématisé par le musicien n’est pas indifférente pour
lui et il faut bien ici comme ailleurs se
battre sur les mots s’il est vrai, comme chacun en fin de compte le sait
fort bien, que céder sur les mots, c’est alors avoir
cédé sur les idées.
Que, contrairement à ce que formule Philippot,
l’application des mathématiques à la musique concerne
l’ontologie et l’ontique, non la logique, laisse alors
grand-ouverte la question de savoir ce qu’est la logique
musicale — je me suis déjà longuement expliqué
sur ce point ; je n’y reviendrai pas aujourd’hui —.
Aujourd’hui, je poserai seulement la question
suivante : selon quelle logique proprement musicale telle ou telle « application »
des mathématiques à la musique pourra-t-elle être
considérée par le musicien comme pertinente ou comme proprement insensée ?
2) Seconde remarque
Philippot, comme Babbitt, tend à rabattre un système musical sur une structure mathématique. Plus exactement, Philippot
opère la série de réductions suivantes : composer, c’est composer un système, donc des structures dont l’intelligence nous est donnée par
la mathématique,
essentiellement par l’algèbre ; soit les enchaînements suivants :
composer ®
système ®
structure ®
mathématique ® algèbre
Remarquons : on descend cette chaîne selon un
ordre de causalité sans se soucier ensuite de la remonter, sans trop
s’occuper donc de savoir ce que le point d’arrivée de cette
chaîne (l’algèbre mathématique en l’occurrence)
a pu perdre en cours de route de la composition musicale posée à
l’origine, a pu effacer de la nature proprement musicale des objets ainsi
traités… D’où une porte ouverte à tous les
obssessionnels de l’algèbre car cette chaîne
« déductive » suggère qu’on pourrait
remonter ce cours c’est-à-dire manipuler des structures
algébriques en sorte d’en
déduire des systèmes
dont la mise en œuvre musicale vaudrait ipso facto composition…
Mon commentaire sur le débat Philippot-Babbitt
s’arrêtera à ces deux remarques. Je ne souhaite pas rouvrir
ici le vaste débat des rapports entre mathématiques et
musique : nous l’avons exploré pendant un an dans le cadre du
séminaire mamuphi et un prochain
livre édité par l’Ircam va cet été mettre en
circulation les termes de ce débat.
*
Je voudrais aujourd’hui me demander plutôt de
quelle manière l’algèbre mathématique nous aide
à penser la combinatoire musicale.
Qu’elle nous aide à la calculer est
évident, et c’est bien à ce titre que tout un chacun y
recourt ordinairement : l’informatique musicale y fait ainsi ses
bénéfices. Mais je pose la question suivante :
l’algèbre mathématique aide-t-elle à penser, et pas
seulement à calculer la combinatoire musicale ?
Pour thématiser cette question qui engage une
pensée des rapports entre mathématiques et musique, je recourrai
une fois de plus à la théorie mathématique des
modèles qui est une manière intra-mathématique de
réfléchir les rapports entre mathématiques et un autre
domaine d’expérience qu’elles-mêmes.
Petite remarque préalable.
Il est a priori trois grands types de méthode pour
penser les rapports entre mathématiques et musique :
1) Un type proprement mathématique. Je
privilégie ici la théorie mathématique des modèles
(qui fait classiquement partie de la logique mathématique) mais on
pourrait en aborder d’autres.
2) Un type de méthode qui serait proprement
musical. À dire vrai, je n’en connais guère. Je peux
seulement indiquer que toute une part de mon travail de
compositeur — cette part pensive que j’appelle intellectualité
musicale — tend à le constituer,
à l’inventer, à le produire.
3) Reste un type qui serait proprement philosophique.
Il s’agirait cette fois d’examiner de quelle manière
mathématiques et musique sont en pensée contemporaines, de quelle
manière ces deux disciplines se conditionnent réciproquement,
etc.
Je privilégierai aujourd’hui la première
méthode car c’est elle qui offre l’avantage
d’être le mieux formalisée.
Je résumerai le fonctionnement de la théorie
mathématique des modèles au moyen du petit diagramme
suivant :

Un modèle
est formalisé par construction
d’une théorie ad
hoc ; puis les résultats de cette théorie sont interprétés dans le modèle ce qui tend à mettre au
jour des réalités inaperçues dans le modèle. Cette
dynamique rend compte de l’intérêt du détour
théorique, en particulier en termes de puissance de calcul. Le diagramme
suivant illustre ce mouvement :
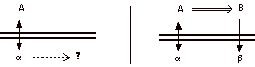
On se demande s’il existe d’autres objets
musicaux tels que a. Le détour par la théorie permet de
générer d’autres objets mathématiques tels que
A : par exemple B. L’interprétation de B dans le champ
musical pointe alors l’objet ß recherché.
Pour donner un exemple concret de ce mouvement : quand
je me demande s’il existe d’autres séries dodécaphoniques
« tous intervalles » que la série de Berg {la,
la#, sol#, si, sol, do, fa#, do#, fa, ré, mi, ré#}, la
formalisation mathématique du problème — la
série des intervalles se formalisera numériquement ainsi :
{1, 10, 3, 8, 5, 6, 7, 4, 9, 2, 11, 6} — va me permettre de calculer
les 1928 formes numériques équivalentes qui
s’interprèteront alors comme 519 séries
dodécaphoniques tous intervalles différentes.
Ainsi la théorisation permet de déduire une
série de résultats lesquels, par interprétation dans le
modèle, élargissent alors le champ des objets musicaux
susceptibles d’entretenir des rapports intéressants avec
l’objet posé au départ.
Cet usage de l’algèbre mathématique
théorisant une combinatoire musicale en vue de calculer toutes les
solutions d’un problème posé en termes musicaux est le plus
ordinaire. Il n’y a pas lieu de le critiquer bien sûr. On peut
simplement se demander dans ce cas dans quelle mesure cet usage principalement
calculatoire de la théorie mathématique permet ou non de mieux
comprendre le problème musical posé, permet ou non de penser plus
avant la combinatoire musicale et pas seulement d’y calculer ;
soit : comment mieux calculer la combinatoire musicale permet-il de mieux
la penser ?
Si l’on se reporte par exemple à
l’article mentionné précédemment de Michel
Philippot, qu’est-ce que le détour par les structures
algébriques — en particulier par la structure de
groupe — permet aux yeux même de Philippot de mieux penser
quant à la musique ? À relire l’article sous cet
angle, pas grand chose n’est en vérité
dégagé, et ce manque n’est pas sans importance à mes
yeux : il me semble un défaut, inclinant le musicien à
adopter la thèse de Thomas d’Aquin et de Leibniz plutôt
qu’à doter la musique d’une autonomie de
pensée…
Il ne me semble donc pas indifférent pour le
développement à long terme du monde de la musique comme monde
autonome de pensée, non comme champ ludique sans enjeu parmi bien
d’autres, que le musicien s’astreigne à
réfléchir ces calculs que la formalisation mathématique
lui offre généreusement : il importe que cette
réflexion, que la mathématique poursuit pour son propre compte
dans le champ par exemple de la théorie des modèles, la musique
le fasse aussi pour son compte propre sans en déléguer la
responsabilité à la philosophie. Il en va là de
l’existence ou non d’une intellectualité musicale, et
l’on peut penser que de cette existence dépend qu’il y ait
ou non dans les temps qui viennent les musiciens aptes à répondre
aux défis posés par ces temps à la musique…
Pour contribuer à élargir le
déploiement d’une telle intellectualité musicale, je
voudrais illustrer un autre usage possible de la théorie
mathématique non plus cette fois pour mieux calculer tel ou tel
problème posé en termes de combinatoire musicale mais directement
pour mieux penser ce problème comme tel. J’illustrerai ce nouvel
usage du diagramme suivant :
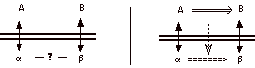
L’idée est la suivante : on se demande
quel rapport musical il peut y avoir entre les deux objets musicaux a et
ß. Pour cela, on va formaliser mathématiquement ces deux objets
(d’où les deux objets mathématiques A et B) et on va alors
se demander quel rapport mathématique il peut y avoir entre A et B
(partie gauche du diagramme). Si l’on arrive alors à produire ce
rapport mathématique (double flèche du second diagramme), on
escompte que celui-ci va suggérer un rapport équivalent,
d’ordre cette fois musical, entre a et ß (soit la
double flèche en pointillé).
Je vais donner deux exemples concrets de cette
démarche, prélevés dans notre espace de travail du jour
c’est-à-dire engageant des problèmes de combinatoire
musicale :
· la
formalisation d’un renversement rétrogradé comme ruban de
Möbius ;
· une
interprétation musicale des pavages apériodiques de Penrose.
Ces deux exemples de combinatoire ont, comme vous allez le
voir, pour caractéristique significative d’être moins des
cas de construction progressive (allant d’éléments
soigneusement sélectionnés aux petites parties qu’il est
possible de former à partir d’eux puis à des regroupements
encore plus vastes) que des cas où formalisation et
interprétation portent d’emblée sur des ensembles
constitués, où combinatoire musicale et algèbre
mathématique opèrent sur des sous-ensembles, des familles de
parties plutôt que sur de simples éléments, des
problèmes donc où la relation qui importe est celle
d’inclusion plus que d’appartenance, bref des situations relevant
de la topologie algébrique plutôt que de l’algèbre
topologique…
Examinons ces deux situations de pensée.
I. Renversement rétrogradé et ruban de Möbius
L’histoire musicale présente de nombreuses
situations où le renversement d’une structure musicale horizontale
(ligne mélodique, série des hauteurs, etc.) s’associe
à sa rétrogradation.
Pour en donner un seul exemple, voici un canon de Mozart qui
se joue simultanément par deux instrumentistes se faisant face et lisant
un même partition de part et d’autre d’une seule table :


Il n’est pas tout à fait strictement la
rétrogradation d’un renversement mais l’esprit de la
combinatoire musicale est bien celui-ci. Le canon obtenu est d’abord
à l’octave puis à la tierce ou la sixte…
Voici un exemple plus strict de renversement
rétrogradé. Je l’extraie d’une des mes
œuvres : Passage II (1985)
pour trois flûtes :
Passage II (pour trois flûtes, 1985 – Éd.
Jobert) : mesures 33-48

Cette fois les opérations combinatoires sont
très strictes, aux altérations près. Pour les mettre en
valeur, voici une seconde présentation de la partition,
dépouillée cette fois de toute notation en sorte de la
réduire à ses seules notes — je les ai parfois
réorthographiées (un si bémol devenant par exemple un la #) et allégées de leurs
altérations en sorte de mettre en évidence la
propriété combinatoire de ce passage — :

Si vous repliez le second système sur le premier
(selon un pli horizontal) vous obtenez alors une superposition exacte qui
indique que ce second système est bien la reprise du premier selon une
inversion générale du haut et du bas comme de l’avant et de
l’après.
Par-delà la dimension ludique de cette combinatoire,
y a-t-il là une visée musicale quelconque ou ceci reste-t-il un
simple jeu sans enjeu ?
Dans Passage II, en
tous les cas, l’enjeu est le suivant : cette rétrogradation
renversée prend place au centre de la pièce et compose un moment
de basculement général du discours musical dont on ne saisit plus
bien, quand on le parcourt à l’audition, s’il est encore
développement ou répétition, s’il est une
avancée ou un retour en arrière. Bref ce passage ainsi composé
et placé là, au centre de l’œuvre, constitue un moment
de vacillation dans la perception d’une progression temporelle, un moment
de désorientation de l’oreille dans le temps.
Pour mieux en comprendre la structure interne, il faut ici,
comme je l’ai indiqué, le retourner pour le déchiffrer par
transparence à l’envers : cette opération
géométrique délivre la vérité combinatoire
ce passage car il indique qu’il s’agit là tout simplement
d’une bande de Möbius qui se trouve parcourue une première
fois la tête en haut et une seconde fois la tête en bas.
L’ensemble de ce passage peut ainsi être conçu comme la circulation
sur une bande de Möbius de huit mesures de long, le second système
ne représentant alors qu’un second tour parcouru à
l’envers du premier.
Finalement cette combinatoire musicale de Passage II peut se formaliser ainsi :
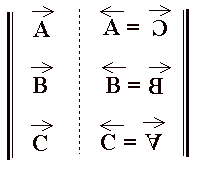
En quoi le fait de nommer « ruban de
Möbius » ce renversement rétrogradé apporte-t-il
quelque chose ou s’agit-il seulement là d’une sorte de
snobisme consistant à rebaptiser des réalités somme toute
vulgaires, en croyant ainsi les anoblir ?
Ce que je veux rapidement vous montrer c’est que cette
formalisation mathématique de la combinatoire musicale va
délivrer une compréhension plus profonde de l’effet musical
visé, une compréhension ontologique et non plus seulement la
constatation empirique d’une propriété.
Je suivrai pour cela le travail d’Albert Lautman
qui propose de distinguer propriétés intrinsèques et propriétés
extrinsèques d’un être.
· Il
appelle propriétés intrinsèques d’un être (ou propriétés
internes, propriétés de structure) les propriétés de cet être
indépendantes de sa position dans l’espace. Elles appartiennent
donc en propre à cet être et constituent ce que Lautman appelle
une analytique.
· Les
propriétés extrinsèques (ou propriétés d’insertion, propriétés
de situation), elles, traduisent la
solidarité d’un être et de l’univers au sein duquel il
est plongé et constituent ce que Lautman appelle une esthétique.
Dans quel cas ces deux types de propriété
sont-elles ou ne sont-elles pas indépendants ? Comment peut-on
concevoir une interaction des unes sur les autres ? Lautman donne ici deux
exemples de démarches philosophiques :
· Leibniz
incarne la voie qui intériorise les propriétés extrinsèques
en les projetant en propriétés intrinsèques. Leibniz tente
en effet de réduire les rapports que la monade soutient avec toutes les
autres monades en propriétés internes, enveloppées dans
l’essence de la monade individuelle. D’où une sympathie
universelle qui se projette en chaque monade, laquelle représente
exactement l’univers à sa manière.
· À
l’opposé Kant postule une stricte distinction sans réduction
possible des unes aux autres en remarquant l’incongruence de figures
symétriques qui ne sont donc pas superposables (telles les mains gauche
et droite). Ces différences entre ces figures résultent en fait
de la différence des places qu’occupent ces corps dans
l’espace sensible et non pas d’une différence dans les
propriétés internes de ces corps. D’où, selon Kant,
une distinction entre la raison qui ne peut
que caractériser de façon abstraite les propriétés
intrinsèques des corps géométriques (raison
analytique donc, pour reprendre les termes
de Lautman) et l’intuition sensible (ou intuition
qu’on pourrait dire esthétique) qui appréhende la position dans
l’espace de ces corps et se réfère à
l’orientation de l’espace entier.
Sur cette base, Lautman examine les propriétés
mathématiques de l’anneau de Möbius et relève la
dualité suivante :
· d’un
côté la bande de Möbius est unilatère (elle a un seule
face) ;
· d’un
autre côté, elle est inorientable.
Il se demande alors s’il y a un lien
mathématique entre ces deux types de propriété sachant que
le fait d’être non-orientable constitue une propriété
intrinsèque de cette bande quand le fait d’avoir un seul
côté constitue pour cette même bande une propriété
essentiellement extrinsèque (par exemple dans un espace non euclidien,
une telle bande peut être bilatère !). On se trouve donc ici
apparemment face à une stricte distinction des propriétés,
un étroit cloisonnement entre propriétés
intrinsèques de structure et propriétés
extrinsèques de situation.
Or — surprise mathématique — on
démontre que dans un espace orientable à n dimensions, il y a pour une variété
à n-1 dimensions
équivalence entre le fait d’être bilatère et le fait
d’être orientable et, réciproquement, équivalence
entre le fait d’être unilatère et le fait d’être
non-orientable. Donc les propriétés géométriques de
relation se laissent ici dans une très large mesure exprimer en
propriétés algébriques intrinsèques et l’on
voit ici s’évanouir la distinction kantienne d’une
esthétique et d’une analytique.
Dit plus simplement, concernant notre bande de Möbius
musicale plongée dans l’espace ordinaire euclidien à trois
dimensions, il y a bien corrélation ontologique entre
propriétés extrinsèques (maniées par
l’écriture et la partition) et propriétés
intrinsèques (appropriées par l’oreille qui parcourt cette
bande au fil d’une écoute constamment locale et immergée
dans le flot musical) c’est-à-dire empiriquement entre la
symétrie inversée pour l’œil et la désorientation
pour l’oreille.
Je ne m’étends pas sur les conséquences
théoriques de tout ceci, en particulier pour articuler soigneusement la
différence entre aspect extérieur d’une œuvre et
ce que j’aime appeler son inspect
(c’est-à-dire sa forme telle que saisie de
l’intérieur même de son déroulement) .
Je veux seulement relever que la formalisation mathématique permet de
saisir pourquoi une opération d’écriture (ou combinatoire
extrinsèque consistant à rétrograder et inverser) est
ontologiquement associable à une propriété
intrinsèque, cette fois de perception sonore et non plus de
déchiffrage visuel.
La formalisation mathématique n’a pas ici pour
vertu de faciliter le calcul musical mais, permettant au musicien de comprendre
le pourquoi d’un effet, elle lui permet de mieux penser ce qu’il
fait artisanalement. Elle peut alors le conduire non seulement à
entreprendre de nouveaux calculs combinatoires de ce même type mais, plus
encore, à imaginer ce que pourrait vouloir dire que de plonger cette
même partition dans un espace cette fois non euclidien.
Je laisse ici ouvert ce champ prospectif : je veux
simplement relever l’effet dynamisant pour l’imagination musicienne
que peut avoir la pensée formalisée.
II. Pavage de Penrose et composition musicale
Venons-en à mon second exemple de combinatoire
(toujours associée à la manipulation de parties musicales
plutôt qu’à un engendrement élémentaire) pour
montrer cette fois comment une formalisation mathématique peut ouvrir la
possibilité d’une existence musicale ; le détour par
l’algèbre mathématique élargit ici la pensée
musicale en donnant droit à certaines formes de pratiques
compositionnelles : celles qui vont du global au local, qui agissent en
peuplant un espace global préformé de parties
prélevées dans une famille donnée. L’exemple canonique
en musique contemporaine est celui de Stockhausen qui, à l’inverse
de la pratique du développement d’un Boulez générant
le tout à partir d’une combinatoire élémentaire,
vise plutôt à occuper une totalité
pré-délimitée par mise en jeu d’entités
elles-mêmes pré-formées. On peut également trouver
trace d’un tel type de préoccupation chez un Jean-Sébastien
Bach entreprenant par exemple de composer un choral pour orgue sur la base
d’un cantus firmus préexistant qui lui fournit moins un
thème à développer (cas des fugues dont le sujet est
prélevé dans la tête d’un cantus firmus) qu’une
longue mélodie, structurée en diverses parties, l’enjeu
compositionnel devenant alors d’organiser l’œuvre autour de ce
vaste conduit en sorte qu’il la traverse de part en part. Soit une
école compositionnelle qu’on pourrait appeler celle de
l’occupation (Bach-Stockhausen…) face à celle du
développement (Beethoven-Boulez…).
Vous vous doutez bien que, si je m’intéresse
à cette problématique compositionnelle de l’occupation (qui
va du global au local, à l’inverse du développement
procédant de la partie vers le tout), c’est parce que mon propre
travail compositionnel se nourrit prioritairement de cette dynamique : comment
occuper un espace pré-dimensionné de gestes pré-existants
plutôt qu’à l’inverse jusqu’à quelles
dimensions pousser le développement de telle idée
séminale) ?
Les pavages de Penrose vont ici nous fournir matière
à penser.
La géométrie étudie les différentes
manières de paver le plan. On peut ainsi recouvrir le plan avec deux
formes simples (des « cerfs-volants » et des
« flèches »
dont les proportions géométriques sont fixées selon le
nombre d’or et que l’on ne convient d’assembler que selon
certaines règles spécifiées) qui conduisent à un
pavage non périodique (non périodique voulant dire : qui ne se répète
pas). Voici deux exemples d’un tel pavage dit de Penrose.


La mathématique
démontre alors les deux résultats suivants :
1. Il existe une infinité de manières
différentes de paver le plan avec ces deux tuiles (manières différentes voulant dire : on ne peut passer de l’une
à l’autre par glissement du plan sur lui-même).
2. Par contre tout découpage fini se retrouve
dans toutes les manières. C’est dire qu’il est proprement impossible
de montrer une région (si montrer veut dire exhiber un extrait du pavage, comme le
fait notre dessin) qui ne se retrouverait dans toutes les manières.
Aucun moyen donc pour l’œil de savoir qu’il n’y a pas
une seule manière de paver mais bien une infinité. Notre
œil, attaché au fini, ne saurait suivre ici la raison dans sa
compréhension de l’infini.
Ces résultats mathématiques éclairent
déjà un point musical capital : l’écoute
musicale, relevant d’une pensée corrélant le sensible
à l’intelligible, se lève au point
où le sensible ne se cantonne plus au régime du perceptible pour
s’ouvrir à un nouveau principe d’intelligibilité ne
relevant plus du montrable mais inaugurant la rationalité musicale
d’infinités non représentables. Ou encore : de
même que dans les pavages de Penrose la raison sait ce que
l’œil ne saurait voir, de même en musique
l’écoute « intelligente » entend
au-delà de ce que l’oreille perçoit.
Mais je voudrais convoquer ces pavages pour d’autres propriétés,
plus combinatoires.
Le point qui m’importe est le suivant : on
démontre qu’il existe une isomorphie locale de ces pavages
c’est-à-dire que chaque échelle de pavage correspond
biunivoquement à un autre pavage apériodique du même type
mais à une échelle immédiatement supérieure et
à une échelle immédiatement inférieure selon
certains principes précis de composition/décomposition des
tuiles. Le schéma suivant illustre le mouvement de composition des
tuiles conduisant à de plus vastes tuiles de mêmes formes :
Tuiles
« cerfs-volants » et
« flèches » :
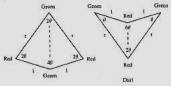
Changement
d’échelle des tuiles :
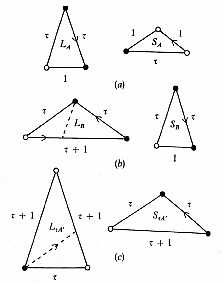
Changement
d’échelle du pavage :

Le point remarquable est alors le suivant : on montre
que si on se donne à la fois un jeu de tuiles d’une échelle
donnée et une forme globale qu’il s’agit de recouvrir par
les premières, on ne saurait y arriver par ajout successif de tuiles
élémentaires, par extension progressive d’un noyau initial
et que le seul moyen d’y parvenir est de suivre un plan global
d’occupation de cet espace pré-défini.
Remplissage
d’une « roue » :
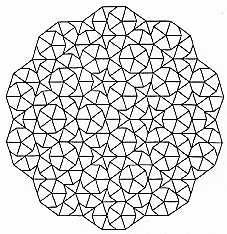
Vous le comprendrez intuitivement : la loi
d’isomorphie locale mentionnée précédemment va
impliquer un travail de décomposition plutôt que de composition
c’est-à-dire va circuler d’un plan global fixant les quelques
tuiles de grande échelle aptes à recouvrir notre forme
pré-définie pour ensuite les décomposer en des
échelles progressivement plus petites de tuiles jusqu’à
arriver à l’échelle minimale des tuiles. Vous voyez
l’équivalent avec notre problème musical : la
composition ici doit être avant tout une décomposition, disons une
analytique progressivement déployée à partir d’une
proposition initialement synthétique.
Si vous opérez à l’inverse, par
combinaison de proche en proche des tuiles d’échelle minimale,
vous aboutirez nécessairement à un trou que vous ne pourrez
combler avec votre outillage si bien que prolonger éventuellement votre
développement au-delà de ce trou ne pourra plus se faire
qu’en le contournant.
Trou
« essentiel » :

Les mathématiciens ont exploré la forme de ces
trous et ont démontré qu’il y avait 61 formes
différentes pour ceux de ces trous qui s’avèrent
« essentiels » .
Petite digression
Tout ceci, qui nous intéresse pour la composition musicale — j’y
reviendrai —, intéresse également les cristallographes.
Ceux-ci étudient en effet les cristaux naturels
générés par concrétion progressive à partir
d’un noyau et avaient exploré ainsi les différentes formes
de pavage de l’espace. L’idée s’était
naturellement imposée que dans la nature les cristaux ne pouvaient
n’être donc que périodiques puisque leur dynamique
même de constitution était à la fois progressive (allant du
plus petit au plus grand) et homogène. Or les cristallographes ont
découvert des structures naturelles apériodiques pour lesquelles
l’impératif précédemment indiqué
s’appliquait parfaitement : comme on ne peut générer
de tels pavages de proche en proche mais qu’il faut un plan
d’ensemble pour arriver à paver sans trou le volume avec les
cristaux élémentaires les plus basiques, ceci voudrait-il donc
dire qu’un architecte se tenait ici en embuscade, dirigeant secrètement
l’édification du cristal en fonction de la taille à
atteindre ? L’existence de ces quasi-cristaux (ou structures
cristallines apériodiques) constituerait-elle ainsi une preuve de
l’existence de Dieu, tout du moins d’un dieu du cristal ?
L’élucidation de ce mystère tient au
fait qu’il est très facile de générer une structure
apériodique à partir d’une structure entièrement
périodique : il suffit simplement que cette dernière soit
d’une dimension supérieure à la première et que la
première en soit une projection particulière.
Pour illustrer ce point il suffit de voir qu’une
droite traversant un quadrillage régulier se verra striée
d’intervalles périodiques si elle croise ce quadrillage en aux
deux points. Mais si cette droite ne rencontre qu’un point de tout ce
quadrillage (ce qui est simplement dire que sa pente est réglée
par un rapport irrationnel), alors les segments qui y seront
découpés par le quadrillage seront apériodiques.
Apériodicité
par projection diagonale d’une périodicité
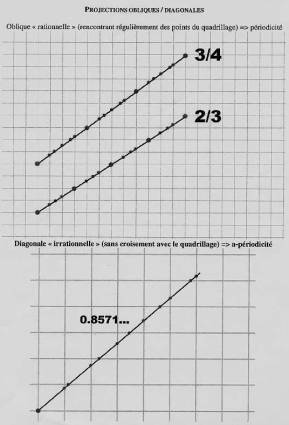
Dans le cas des quasi-cristaux considérés (en
trois dimensions), l’apériodicité du pavage
s’obtenait par projection d’une structure périodique dans un
espace à cinq dimensions.
Revenons à l’interprétation musicale de
notre composition/décomposition.
La théorie mathématique des pavages
apériodiques de Penrose rend à mon sens raison de ce point :
il n’est pas vrai que la composition musicale soit essentiellement
développement. Elle peut être aussi — elle doit
être également — occupation. Ou encore : elle
n’est pas seulement conquête de nouveaux territoires mais
peut-être aussi — doit être
également — peuplement de territoires découverts. Soit
les deux grandes voies compositionnelles que j’ai appelées celles
de Beethoven-Boulez et celle de Bach-Stockhausen (rappelons au passage que le
jeune Boulez indexait le Clavier bien tempéré à un « manifeste
d’occupation » de l’espace tonal tempéré
qui était offert à Bach par son époque sans qu’il
ait eu besoin de le conquérir. J’ajouterai que les forces que Bach
convoquait pour cette occupation était celles de la polyphonie et du
contrepoint et qu’il disposait ainsi musicalement à la fois
d’un espace stratégique et des forces aptes à l’occuper…).
Dans la problématique compositionnelle du
développement, le lien entre idée de base (geste initial,
thème de départ…) et forme engendrée est
capitale : c’est ici le thème qui engendre la forme. Dans la
composition conçue comme occupation d’une forme, comme prise de
possession d’un espace, comme appropriation d’un lieu, comme
emprise sur une intervalle de temps, comme contrôle exercé sur une
vaste durée, le lien est tout autant étroit entre matériau
de base et forme globale si bien que l’inspiration du compositeur
consiste en vérité à se donner le couple singulier des
deux, un peu comme Beethoven se donnait à la fois un thème et la
grande forme symphonique qu’il serait en état de
générer …
Ainsi l’algèbre mathématique (ici cette
manière très moderne d’algébriser la
géométrie) donne-t-elle à penser sur la combinatoire
musicale par-delà les cas — les plus nombreux, il est
vrai — où elle l’aide à calculer.
Il me semble nécessaire d’en revenir à
cette manière de voir les choses si l’on souhaite prolonger
l’alliance mathématiques—musique sans retourner à la
manière dont une certaine application de l’algèbre à
la combinatoire musicale a pu servir de paravent pour dissimuler une indigence
de pensée proprement musicale.
Et je terminerai sur cette remarque : rehausser la
dimension de pensée de la mathématique et pas seulement sa
puissance incomparable de calcul me semble une ressource dont ne sauraient se
priver les musiciens qui ne se satisfont pas d’un état purement
artisanal de la composition musicale.
–––
Bibliographie de François Nicolas
sur Musique et mathématiques
Musique et mathématiques
· “Partages
d’écriture : Mathématique et Musique sont-elles
contemporaines ?” Cahiers du CREM (n° 1-2, 1986)
· “Nombre,
note et oeuvre musicale” Actes de la 3° ICMPC (Liège, 1994)
www.entretemps.asso.fr/Nicolas/TextesNic/nombre.html
· “Musique,
mathématiques et philosophie : que vient faire ici la
philosophie ?” (Ircam, 7 octobre 2000, Séminaire Entretemps
www.entretemps.asso.fr/Nicolas/TextesNic/MathMusPhi.html
· “Y a-t-il une connivence
singulière entre musique et mathématiques ?
Évaluation critique” (Bobigny, janvier 2003)
www.entretemps.asso.fr/Nicolas/TextesNic/Bobigny.html
· “Penser
la musique avec les
mathématiques ?” (Livre collectif à paraître aux
éditions Ircam, 2003)
www.entretemps.asso.fr/Seminaire/mamuphi.html
Logique musicale
· “Qu’est-ce
qu’une logique musicale ?” (décembre 1999, Forum
Diderot, Ircam)
www.entretemps.asso.fr/Nicolas/TextesNic/Diderot/LogiqueDiderot.html
· “Qu’espérer des
logiques musicales mises en œuvre au XX° siècle ?” -
in “Musique contemporaine /
Perspectives théoriques et philosophiques” (dir. I. Deliège
et M. Paddison - Mardaga, 2000)
www.entretemps.asso.fr/Nicolas/TextesNic/LogiqueBruxelles.html
· “Questions
de logique : écriture, dialectique et stratégie musicales”
- paru en anglais (Questions on logic: writing, dialectics and musical
strategies) chez Springer-Verlag in Mathematics and Music, 2002
www.entretemps.asso.fr/Nicolas/TextesNic/QuestionsDeLogique.html
www.entretemps.asso.fr/Nicolas/TextesNic/QuestionsOfLogic.html
Musique et informatique
· “Musique
et ordinateur : quelques questions” Entretemps (n° 10, 1992)
www.entretemps.asso.fr/Nicolas/TextesNic/ETS10.html
· “Le
problème de la double écriture (traditionnelle et
informatique)” in Analyse et
création musicales (L’Harmattan, 2001) et le cahier
d’analyse sur Dans la distance
(Marc Battier – Ircam, 1997)
www.entretemps.asso.fr/Nicolas/TextesNic/DLDcahier.html
Divers
Lettres musicale et mathématique
· “De
l’instance de la lettre dans la musique” (Quarto,
n° 65 : Les Lettres de la jouissance, 1998)
www.entretemps.asso.fr/Nicolas/TextesNic/DEA.html
Audition musicale et intégration mathématique
· “La troisième audition est
la bonne (De l’audition musicale conçue comme une
intégration) ” Musicæ Scientæ (n° 2, 1997)
www.entretemps.asso.fr/Nicolas/TextesNic/Audition3.html
Diagonales musicale et mathématique…
· “Le style diagonal de
pensée : une volonté musicale non constructiviste” in Musique, rationalité,
langage — Cahiers de philosophie du langage n° 3, L’Harmattan,
1998)
www.entretemps.asso.fr/Nicolas/TextesNic/SDP.html
Albert Lautman
· “Quelle
unité pour l’œuvre musicale ? (Une lecture d’A.
Lautman)” Conférence Horlieu (Lyon, 1996)
www.entretemps.asso.fr/Nicolas/TextesNic/Lautman.html
Michel Philippot
· “Ce
doit être ! (Essai sur les écrits de Michel Philippot)”
in Michel. Philippot (Éd.
Entretemps, 1994)
www.entretemps.asso.fr/Nicolas/TextesNic/Cedoitetre.html
· “Michel
Philippot, un nom qui demeure” Bulletin de l’Association Michel
Philippot (n° 1, 1996)
www.entretemps.asso.fr/Philippot/bulletin1.html
· “Michel
Philippot et la recherche musicale” in Radios et télévision au temps des
événements d’Algérie (L’Harmattan, 1999)
Iannis Xenakis
· “Le
monde de l’art n’est pas le monde du pardon” Entretemps
(n° 6, 1988)
www.entretemps.asso.fr/Nicolas/TextesNic/Xenakis.html
––––––