Plaidoyer pour une raisonance musique-mathématiques
(Enst-Bretagne, 3
février 2005)
François Nicolas
(compositeur,
professeur associé à l’Ens)
[ Voir aussi la présentation
PowerPoint ]
Plan
2 pensées 3
Mise en rapport… 3
Pourquoi ? 3
Pour le mathématicien… 3
Ontologie… 3
Application 3
Inspiration 3
Pour le musicien… 4
Calcul 4
· Un exemple 4
Pensée : raison + calcul 5
· Axiomes 5
· Théorèmes logiques… 5
— Gödel 5
— Lowenheim-Skolem 5
— Henkin 5
· Ingénieur et matheux 5
Rationalité 6
· Démonstration ? 6
— Parménide :
Fragment VIII 6
· Musicien pensif 6
— Deux
sortes de musiciens… 6
Exemples 6
· Dans la composition 6
· Pour l’intellectualité
musicale 10
Deux modalités donc 11
Affinité d’écriture 11
Écriture mathématique 11
Écriture musicale 11
2 pensées à la lettre 11
Comment mettre en raisonance
musique et mathématiques ? 12
Logique et mathématique 12
Trois modalités 12
Métaphore 12
· Exemple 12
Analogie 12
· Exemple 12
Fiction 13
· Exemple 13
— Intégration
et audition 14
Intérêt de la philosophie 14
Lautman 14
Badiou 14
Exemples pour l’intellectualité musicale 14
Ma liste… 14
Exemple pour la composition 15
La « question » musicale… 15
Son éclairage par raisonance mathématique… 15
Références 21
Un livre 21
Des articles 21
Un séminaire 21
Un site 21
Une liste 21
Annexe 1 : Mozart 22
Annexe 2 : Différentes manières de rapporter les
mathématiques à la musique… 23
Comment mettre en rapport ces deux disciplines, ces deux pensées ?
2 pensées
Cf. thèse : musique et mathématiques sont des pensées, pas des techniques, ou des jeux.
· Musique = pensée de l’écoute, de ce que c’est qu’écouter ; pensée musicale en acte et pas en discours, différente donc du discours musicien (par exemple celui que je tiens devant vous).
· Mathématiques = pensée de l’être pur, de l’être comme être ; pensée mathématique en acte : axiomes, démonstrations, théorèmes, etc.
Mise en rapport…
Ces deux pensées n’ont aucune raison de se rencontrer par elles-mêmes : elles opèrent dans des mondes différents et disjoints.
Leurs éventuels rapports découleront donc d’une mise en rapport.
Pourquoi une telle mise en rapport ? Comment une éventuelle mise en rapport ?
Pourquoi ?
Les raisons ne seront pas les mêmes pour un mathématicien ou pour un musicien.
Je suis musicien, certes doté d’une formation scientifique mais qui n’est pas mathématicien actif (working mathematician disent les anglophones). J’attaque donc ces rapports à partir du versant-musique, mais je connais bien l’autre manière de l’aborder : selon le versant-mathématique (cf. séminaire Ircam puis Ens).
Il me semble que les enjeux de cette mise en rapport sont plus intenses pour les musiciens que pour les matheux : disons que la musique a sans doute plus besoin des mathématiques que l’inverse. En tous les cas, parlant ici en musicien, je mettrai mon exposé sous l’intitulé de la paire ordonnée « musique et mathématiques » et non celle, inverse, qui intitule une telle journée dans l’enceinte d’une école scientifique.
Examinons séparément ces deux versants.
Pour le mathématicien…
Pour la mathématique, la musique est un domaine parmi d’autres qui se présente spontanément comme un lieu particulier d’application.
Ontologie…
Ceci vient de ce que la mathématique pense abstraitement ce qui est, pense les propriétés de ce qui est au seul titre du fait qu’il est ; la mathématique pense l’être comme pur être (c’est à ce titre que le philosophe Alain Badiou déclare que « la mathématique est l’ontologie »). Ainsi les énoncés mathématiques, étant valables pour tout être, sont de facto valides pour tout étant, pour tout ce qui est : s’il est vrai que 7+5=5+7=3*4=4*3=14-2=42/6=12, alors ceci vaut quelles que soient les unités considérées (les « étants » décomptés) : pour des tomates, des notes de musique, ou des étudiants…
Application
Donc pour le matheux, la musique est un champ parmi d’autres où appliquer ses théorèmes généraux — sur les groupes, la décomposition en nombres premiers, la symétrie ou la commutativité —, un champ parmi d’autres dont faire la théorie (mathématique, s’entend). En effet il existe des théories mathématiques de la musique. La plus récente, la plus déployée : celle de Guerino Mazzola exposée dans Topos of music.
Inspiration
Cependant pour un matheux, la musique peut être aussi autre chose : une source d’inspiration, un lieu où certaines intuitions peuvent germer. C’est le sens du séminaire organisé cette année à l’Ens (« Les mathématiciens et la musique »).
De ces deux types de rapport des mathématiciens à la musique, le musicien en général (je suis ici une exception) n’en sait rien : il n’a pas en général les compétences pour examiner les théories mathématiques de la musique (il ne les a pas car il ne cherche tout simplement pas à les avoir), et quant à l’inspiration éventuelle du mathématicien par la musique, le musicien n’en sait rien parce que le mathématicien garde cet aspect pour lui et que le musicien ne s’en enquiert pas : à quoi lui servirait en effet de le savoir ?
Pour le musicien…
Vu du côté de la musique, le rapport musique-mathématiques se présente tout autrement.
Là aussi deux figures :
Calcul
La première, qui est la forme prédominante, est celle du calcul : le musicien s’intéresse aux mathématiques — plus exactement à leurs résultats — pour leur capacité à calculer ce que lui ne sait pas calculer, ou bien mal, et bien laborieusement.
· Un exemple
Je travaille sur des accords que j’appelle « arc-en-ciel » car ils incluent non seulement les 12 hauteurs différentes de la gamme tempérée mais les 11 intervalles différents qu’elle autorise.
Exemple (Dans la distance) :


Le premier exemple d’un tel accord se trouve chez Alban Berg (Suite lyrique) :

Vous pouvez très facilement obtenir une version triviale d’un tel accord en zigzaguant de part et d’autre d’une note pivot :
![]()
Ce type d’accord m’intéresse pour des raisons musicales sur lesquelles je ne m’étends pas ici mais qui sont faciles à intuitionner : il compose un réservoir à la fois complet et non redondant de hauteurs et d’intervalles dans lequel je peux prélever à loisir un matériau diversement coloré…
Là où intervient le calcul, c’est lorsqu’il s’agit de trouver un accord « arc-en-ciel » de ce type : rien n’est moins simple car vous n’y arriverez pas par simple succession empirique. Et si vous y arrivez par une méthode « à la main », vous serez tellement content de votre succès que vous n’entreprendrez pas d’en trouver d’autres.
En ce point le calcul informatisé (dont il ne faut jamais oublier que la base vient des mathématiques) va vous fournir très vite un ensemble beaucoup plus vaste et complet de solutions : on sait par ce détour qu’il y a en fait 1928 solutions différentes qu’il faut repérer dans un ensemble de possibles de 39 916 800. C’est vous dire la difficulté d’aller trouver à la main une seule solution : il vous faut à chaque fois en écarter 20 000 pour en trouver une seule répondant à votre cahier des charges.
Qu’indique cet exemple ?
Le musicien se tourne vers les mathématiques pour lui demander de calculer ce que lui musicien ne sait pas faire, ou trop mal faire. Telle est la voie la plus commune : le musicien ne s’intéresse aux mathématiques que par leur puissance de calcul, en demandant alors que cette puissance se mette à son service.
Pensée : raison + calcul
Le point important est que, ce faisant, le musicien ne s’intéresse aucunement à ce qui de la pensée mathématique ne se réduit pas au calcul.
Le point est en effet que la pensée mathématique est un tricotage étroit entre rationalité et calcul dans lequel la part du calcul est certes capitale et centrale mais n’éponge nullement à elle seule la pensée mathématique.
Que pensée mathématique soit l’enchevêtrement d’une raison et d’un calcul peut être illustré par les quelque points suivants :
· Axiomes
Un axiome, par définition, n’est pas démontré, donc pas calculé. Il est décidé. Mais cependant la décision d’un axiome est un acte relevant de la rationalité mathématique (laquelle excède donc la puissance de calcul).
· Théorèmes logiques…
Quelques grands théorèmes logiques thématisent de même les
excès réciproques de la raison mathématique et du calcul. Donnons-en trois.
— Gödel
Le premier, très connu, le théorème de Gödel, démontrant qu’il y a de l’indécidable, démontre par là que le calcul ne saurait éponger la raison. Remarquons le paradoxe : on démontre, donc on calcule, qu’il y a de l’incalculable, et cet incalculable se trouve ainsi non pas rejeté dans l’irrationnel mais intégré à la rationalité : comme sa part non calculable.
Attention : cette délimitation dans le rationnel entre le calculable et l’incalculable se fait en situation, non pas en soi, si bien que ce qui est incalculable dans une situation peut devenir calculable dans une autre, le point essentiel étant que dans toute situation rationnelle, il y a un point de cette rationalité qui n’est pas calculable de l’intérieur même de cette situation.
Ce point incalculable prescrit une décision (puisqu’on ne peut le trancher par une procédure d’inférences) et cette décision relève en droit des attributs de la rationalité.
— Lowenheim-Skolem
Le deuxième théorème, inverse du précédent — le théorème de Lowenheim-Skolem — va cette fois circonscrire un excès du calcul sur le rationnel en démontrant que toute théorie, constituée pour rendre compte de la singularité d’un champ donné, s’avère rendre également compte, exactement dans les mêmes termes, d’un tout autre champ, entièrement étranger à celui qu’elle visait. En ce sens toute théorie, c’est-à-dire tout système réglé de calcul et d’inférences, rate la singularité du champ qu’elle théorise et le confond nécessairement avec un autre champ, hétérogène et quasi-pathologique au regard de la visée première.
— Henkin
Le troisième théorème, le théorème d’Henkin, plus extraordinaire encore, démontre que toute théorie cohérente a de ce seul fait un modèle, c’est-à-dire que la cohérence d’une théorie garantit l’existence d’un champ où cette cohérence fait sens. En un sens, tout calcul génère une rationalité signifiante.
On a donc une double torison ou double excès entre raison et calcul puisque chacun excède l’autre mais pas aux même points…
· Ingénieur et matheux
J’insiste sur tout ceci, car le musicien, en un sens, est assez proche subjectivement du point de vue de l’ingénieur qui, lui aussi, s’intéresse spontanément aux mathématiques pour ces résultats calculables plutôt que pour sa rationalité démonstrative :
· Cf. les formulaires pour ingénieurs
· Cf. différence entre technicien et matheux : indifférence à la démonstration
· Cf. rapports différents aux équations du physicien (une équation, pour lui, est un outil de pensée, un moment dans la formalisation d’une idée) et de l’ingénieur (pour lui, une équation est un dogme)…
Rationalité
Autre manière, cette fois pour le musicien pensif, de s’intéresser aux mathématiques.
S’intéresser à la pensée mathématique comme telle, à sa rationalité (dont le cœur est la procédure démonstrative), et s’en inspirer soit pour la composition, soit pour l’intellectualité musicale.
· Démonstration ?
Cf. naissance au VI° siècle av. J.-C.
Avant mathématiques babyloniennes, égyptiennes, etc. = calcul.
Mathématiques grecques : démontrées.
Cf. la démonstration (via le raisonnement apagogique) vient de la philosophie : Parménide (fragment VIII de son Poème) :
—
Parménide : Fragment VIII
(Le poème, trad. Jean Beaufret – Puf, 1955)
Il ne reste donc
plus qu’une seule voie dont on puisse parler, à savoir qu’il [l’être]
est ; et sur cette voie, il y a des signes en grand nombre indiquant qu’inengendré,
il est aussi impérissable ; il est en effet de membrure intacte, inébranlable et sans
fin ; jamais il n’était ni ne sera, puisqu’il est maintenant, tout entier
à la fois, un, d’un seul tenant ; quelle génération peut-on rechercher
pour lui ? Comment, d’où serait-il venu à croître ?… Je ne te
permettrai ni de dire, ni de penser que c’est à partir de ce qui n’est pas ;
car il n’est pas
possible de dire ni de penser une façon pour lui de n’être pas. Quelle
nécessité en effet l’aurait amené à
l’être ou plus tard ou plus tôt, s’il venait du rien ? Ainsi donc il est nécessaire qu’il soit absolument
ou pas du tout.
Jamais non plus la fermeté de la conviction ne concédera
que de ce qui est en quelque façon vienne quelque chose à côté de lui ; c’est
pourquoi la justice n’a permis, par
aucun relâchement de ses liens, ni qu’il naisse ni qu’il périsse, mais
maintient ; [la décision à cet égard porte sur cette alternative :] ou
bien il est, ou bien il n’est pas. Il est donc décidé, de toute nécessité, qu’il
faut abandonner la première voie, impossible à penser et à nommer – car elle n’est pas la route de la vérité –, c’est l’autre au contraire
qui est présence et vérité. Comment ce qui est pourrait-il bien devoir
être ? Comment pourrait-il être né ? Car s’il est né, il n’est pas, et il n’est pas non
plus s’il doit un jour venir à être. Ainsi la genèse est éteinte et hors d’enquête le
périssement.
On a là le plus ancien raisonnement par l’absurde de
l’histoire
Il s’agit de démontrer que l’être est inengendré (que
« l’être est sans naître »)
Supposons pour cela à l’inverse qu’il ait été engendré.
Alors, deux possibilités :
il l’a été ou bien par le non-être, ou
bien par l’être.
·
Or ce ne peut pas être par ce qui n’est pas :
« Quelle nécessité l’aurait amené à l’être s’il venait du rien ? »
·
Mais cela ne peut être également par l’être
c’est-à-dire à partir de lui-même : « Comment ce qui est
pourrait-il être né ? Car s’il est né, il n’est pas. »
Donc il n’est pas possible qu’il
ait été engendré..
Or, il n’y a là que deux possibilités : être ou
n’être pas (engendré) : « il
est nécessaire qu’il soit absolument ou pas du tout ».
Donc (« ainsi donc il est nécessaire que… », « il est donc décidé, de toute
nécessité, que… ») il est inengendré.
· Musicien pensif
Cet intérêt du musicien pour la pensée mathématique comme telle, par-delà sa simple application calculatoire, est celui du musicien pensif.
— Deux sortes de musiciens…
Artisan / pensif…
Exemples
· Dans la composition
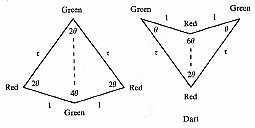
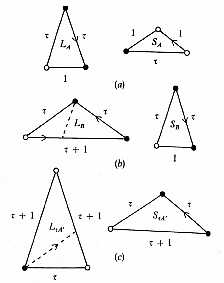
Partons d’une structure mathématique, topologique en l’occurrence : la bande de Möbius
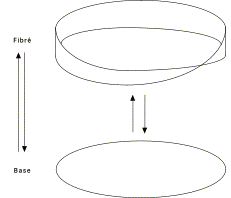
Remarque : cette structure topologique peut très simplement s’algébriser : cf. ce taquin
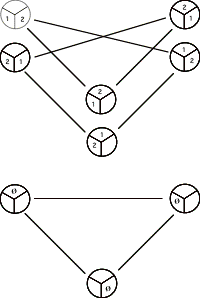
On peut rapprocher cette structure mathématique d’une structure musicale.
L’histoire musicale présente en effet de nombreuses situations où le renversement d’une structure musicale horizontale (ligne mélodique, série des hauteurs, etc.) s’associe à sa rétrogradation.
Pour en donner un seul exemple, voici un canon de Mozart qui se joue simultanément par deux instrumentistes se faisant face et lisant un même partition de part et d’autre d’une seule table :
Voir partition en annexe
En fait, ce canon n’est pas tout à fait strictement la rétrogradation d’un renversement mais l’esprit de la combinatoire musicale est bien celui-ci. Le canon obtenu est d’abord à l’octave puis à la tierce ou la sixte…
Voici ce que cela donne — ce n’est pas musicalement passionnant… — :


Voici un exemple plus strict de renversement rétrogradé. Je l’extraie d’une des mes œuvres : Passage II (1985) pour trois flûtes :
Passage II (pour trois flûtes, 1985 – Éd. Jobert) : mesures
33-48


Cette fois les opérations combinatoires sont très strictes, aux altérations près. Pour les mettre en valeur, voici une seconde présentation de la partition, dépouillée cette fois de toute notation en sorte de la réduire à ses seules notes — je les ai parfois réorthographiées (un si bémol devenant par exemple un la #) et allégées de leurs altérations en sorte de mettre en évidence la propriété combinatoire de ce passage — :

Si vous repliez le second système sur le premier (selon un pli horizontal) vous obtenez alors une superposition exacte qui indique que ce second système est bien la reprise du premier selon une inversion générale du haut et du bas comme de l’avant et de l’après.
*
Par-delà la dimension ludique de cette combinatoire, y a-t-il là une visée musicale quelconque ou ceci reste-t-il un simple jeu sans enjeu ? Comme on va le voir, la rationalité mathématique va ici nous éclairer.
Dans Passage II, en tous les cas, l’enjeu est le suivant : cette rétrogradation renversée prend place au centre de la pièce et compose un moment de basculement général du discours musical dont on ne saisit plus bien, quand on le parcourt à l’audition, s’il est encore développement ou répétition, s’il est une avancée ou un retour en arrière. Bref ce passage ainsi composé et placé là, au centre de l’œuvre, constitue un moment de vacillation dans la perception d’une progression temporelle, un moment de désorientation de l’oreille dans le temps.
Pour mieux en comprendre la structure interne, il faut ici, comme je l’ai indiqué, le retourner pour le déchiffrer par transparence à l’envers : cette opération géométrique délivre la vérité combinatoire ce passage car il indique qu’il s’agit là tout simplement d’une bande de Möbius qui se trouve parcourue une première fois la tête en haut et une seconde fois la tête en bas. L’ensemble de ce passage peut ainsi être conçu comme la circulation sur une bande de Möbius de huit mesures de long, le second système ne représentant alors qu’un second tour parcouru à l’envers du premier.
Finalement cette combinatoire musicale de Passage II peut se formaliser ainsi :
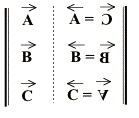
En quoi le fait de nommer « ruban de Möbius » ce renversement rétrogradé apporte-t-il quelque chose ou s’agit-il seulement là d’une sorte de snobisme consistant à rebaptiser des réalités somme toute vulgaires, en croyant ainsi les anoblir ?
Ce que je veux rapidement vous montrer c’est que cette formalisation mathématique de la combinatoire musicale va délivrer une compréhension plus profonde de l’effet musical visé, une compréhension ontologique et non plus seulement la constatation empirique d’une propriété.
*
Comment la raisonance mathématique soutient-elle la pensée musicale ?
Je suivrai pour cela le travail d’Albert Lautman qui propose de distinguer propriétés intrinsèques et propriétés extrinsèques d’un être.
· Il appelle propriétés intrinsèques d’un être (ou propriétés internes, propriétés de structure) les propriétés de cet être indépendantes de sa position dans l’espace. Elles appartiennent donc en propre à cet être et constituent ce que Lautman appelle une analytique.
· Les propriétés extrinsèques (ou propriétés d’insertion, propriétés de situation), elles, traduisent la solidarité d’un être et de l’univers au sein duquel il est plongé et constituent ce que Lautman appelle une esthétique.
Dans quel cas ces deux types de propriété sont-elles ou ne sont-elles pas indépendants ? Comment peut-on concevoir une interaction des unes sur les autres ?
Lautman donne ici deux exemples de démarches philosophiques :
· Leibniz incarne la voie qui intériorise les propriétés extrinsèques en les projetant en propriétés intrinsèques. Leibniz tente en effet de réduire les rapports que la monade soutient avec toutes les autres monades en propriétés internes, enveloppées dans l’essence de la monade individuelle. D’où une sympathie universelle qui se projette en chaque monade, laquelle représente exactement l’univers à sa manière.
· À l’opposé Kant postule une stricte distinction sans réduction possible des unes aux autres en remarquant l’incongruence de figures symétriques qui ne sont donc pas superposables (telles les mains gauche et droite). Ces différences entre ces figures résultent en fait de la différence des places qu’occupent ces corps dans l’espace sensible et non pas d’une différence dans les propriétés internes de ces corps. D’où, selon Kant, une distinction entre la raison qui ne peut que caractériser de façon abstraite les propriétés intrinsèques des corps géométriques (raison analytique donc, pour reprendre les termes de Lautman) et l’intuition sensible (ou intuition qu’on pourrait dire esthétique) qui appréhende la position dans l’espace de ces corps et se réfère à l’orientation de l’espace entier.
Sur cette base, Lautman examine les propriétés mathématiques de l’anneau de Möbius et relève la dualité suivante :
· d’un côté la bande de Möbius est unilatère (elle a un seule face) ;
· d’un autre côté, elle est inorientable.
Il se demande alors s’il y a un lien mathématique entre ces deux types de propriété sachant que le fait d’être non-orientable constitue une propriété intrinsèque de cette bande quand le fait d’avoir un seul côté constitue pour cette même bande une propriété essentiellement extrinsèque (par exemple dans un espace non euclidien, une telle bande peut être bilatère !). On se trouve donc ici apparemment face à une stricte distinction des propriétés, un étroit cloisonnement entre propriétés intrinsèques de structure et propriétés extrinsèques de situation.
Or — surprise mathématique — on démontre que dans un espace orientable à n dimensions, il y a pour une variété à n-1 dimensions équivalence entre le fait d’être bilatère et le fait d’être orientable et, réciproquement, équivalence entre le fait d’être unilatère et le fait d’être non-orientable. Donc les propriétés géométriques de relation se laissent ici dans une très large mesure exprimer en propriétés algébriques intrinsèques (et l’on voit ici s’évanouir la distinction kantienne d’une esthétique et d’une analytique).
Dit plus simplement, concernant notre bande de Möbius musicale plongée dans l’espace ordinaire euclidien à trois dimensions, il y a bien corrélation ontologique entre propriétés extrinsèques (maniées par l’écriture et la partition) et propriétés intrinsèques (appropriées par l’oreille qui parcourt cette bande au fil d’une écoute constamment locale et immergée dans le flot musical) c’est-à-dire empiriquement entre la symétrie inversée pour l’œil et la désorientation pour l’oreille.
*
Je ne m’étends pas sur les conséquences théoriques de tout ceci, en particulier pour articuler soigneusement la différence entre aspect extérieur d’une œuvre et ce que j’aime appeler son inspect (c’est-à-dire sa forme telle que saisie de l’intérieur même de son déroulement). Je veux seulement relever que la formalisation mathématique permet de saisir pourquoi une opération d’écriture (ou combinatoire extrinsèque consistant à rétrograder et inverser) est ontologiquement associable à une propriété intrinsèque, cette fois de perception sonore et non plus de déchiffrage visuel.
La formalisation mathématique n’a pas ici pour vertu de faciliter le calcul musical mais, permettant au musicien de comprendre le pourquoi d’un effet, elle lui permet de mieux penser ce qu’il fait artisanalement. Elle peut alors le conduire non seulement à entreprendre de nouveaux calculs combinatoires de ce même type mais, plus encore, à imaginer ce que pourrait vouloir dire que de plonger cette même partition dans un espace cette fois non euclidien.
Je laisse ici ouvert ce champ prospectif : je veux simplement relever l’effet dynamisant pour l’imagination musicienne que peut avoir la pensée formalisée.
· Pour l’intellectualité musicale
Voir plus loin : intégration mathématique et audition musicale
Deux modalités donc
Comme on le verra encore mieux dans la suite de cet exposé, l’inspiration peut être vue comme une mise en résonance de deux pensées disjointes. Si l’application-calcul est de l’ordre (dissymétrique) du vecteur ou de la fonction (allant dans le sens des mathématiques vers la musique), l’inspiration est de l’ordre (en droit symétrique) d’une résonance par sympathie : la pensée mathématique de par son propre mouvement intérieur met en branle la pensée musicienne pour peu que celle-ci s’approche d’assez près et s’oriente convenablement.
Affinité d’écriture
Une question reste en plan — avant même que nous
n’examinions quelques figures particulières du « comment rapporter musique
et mathématiques » — : si l’application mathématiques-musique
n’a somme toute rien de privilégié (il y a des applications de la mathématique
à toutes les formes de l’étant), il semble bien par contre qu’il y ait une
affinité particulière entre mathématiques et musique qui se traduit
empiriquement par la fréquence des mathématiciens pratiquant la musique, par
cette aptitude conjointe à faire des mathématiques et à faire de la musique
qu’on constate, je crois, tout au long des études. Il y aurait donc, peut-être,
une base matérielle au fait que musique et mathématiques peuvent s’inspirer de
manière privilégiée.
Ma thèse est ici la suivante : s’il y a bien une
inspiration privilégiée entre musique et mathématiques, c’est parce que ces
deux pensées ont en commun un rapport tout à fait singulier à l’écriture.
Ce serait ici trop long de me lancer dans une histoire
comparée de l’écriture musicale et de l’écriture mathématique.
Je tiens d’ailleurs à indiquer que sur ce sujet comme sur
bien d’autres, Xenakis a écrit des choses stupides et ignorantes : si vous
vous intéressez aux rapports mathématiques-musique, je vous déconseille fortement
de perdre du temps à déchiffrer son galimatias qui, malheureusement, encombre
désormais les rencontres sur ce sujet et détourne de la mathématique les
musiciens bien disposés.
Pour faire ressortir la singularité de ce que j’appelle « un partage
d’écritures » entre musique et mathématiques, je ferai les deux remarques
suivantes :
Écriture mathématique
L’écriture mathématique est la seule véritable écriture
scientifique : depuis Galilée la physique s’écrit en lettres mathématiques
et ce protocole s’impose depuis comme paradigme moderne des sciences (est aujourd’hui
une science véritable non pas seulement un dispositif rationnellement ordonné
de savoirs mais ce qui peut se formaliser mathématiquement — on sait par
exemple les tentatives de la linguistique pour se doter d’une telle
puissance —). La physique, donc, n’a pas d’écriture propre mais s’écrit
avec des lettres mathématiques.
Écriture musicale
D’un autre côté, la musique est le seul art à s’être doté
d’une écriture qui lui soit propre, cette écriture qui s’appelle le solfège et
qui, grosso modo, s’est constituée durant le Moyen-Âge.
Notez bien : la peinture, l’architecture, le cinéma,
même la chorégraphie (en dépit de tentatives en cours, ; non encore abouties)
ne se sont pas dotées d’écritures autonomes proprement dites, c’est-à-dire
d’une inscription à la lettre. La musique l’a fait, et ceci a bouleversé son
cours : c’est grâce à cela qu’il a pu y avoir le contrepoint, la
polyphonie, l’harmonie tonale, le développement rythmique, les grandes formes,
etc.
L’évènement de cette invention de l’écriture musicale (qui n’existait pas par exemple du
temps des Grecs) a été amplement remarqué : pour n’en donner qu’un
exemple, et qui n’est pas des moindres, Descartes a inauguré son entreprise
philosophique par un livre traitant de musique – son Compendium Musicæ — et tentant de penser les conséquences pour la
philosophie de ce qui s’était passé dans la musique (constitution d’un solfège,
naissance d’un ordre musical autonome par rapport à l’ordre arithmétique,
etc.). Il n’en tirera pas moins que l’intuition d’un sujet réflexivement
constitué, le futur « sujet de la science ».
2 pensées à la lettre
Mon hypothèse est ainsi que mathématicien et musicien
partagent un mode de pensée que j’appelle « pensée à la lettre » et
qui constitue la base matérielle pour cette affinité élective entre musique et
mathématiques. N’est-ce d’ailleurs pas une évidence empirique qu’il y a les
mêmes surprises (pour qui n’est pas initié) à voir derrière les lettres
suivantes
x2+y2=c
la figure d’un cercle

et à entendre, derrière les lettres suivantes

le thème de la V° de Beethoven ?

Dans les deux cas, l’écart entre le régime de la lettre et
la figure sensible qui est ici indexé est maximal. C’est, je crois, l’aisance à
se mouvoir dans cet écart qui rapproche le faire et le comprendre la
musique du faire et du comprendre les mathématiques.
*
Voyons maintenant comment il est possible de rapporter
musique et mathématiques. Je me concentrerai ici sur la figure de résonance
entre deux modes disjoints de rationalité, le cas de l’application et du calcul
étant bien sûr beaucoup plus trivial.
Comment mettre en raisonance musique et mathématiques ?
Plaidoyer pour une mise en rapport des mathématiques et de la musique en amont du calcul et des techniques d’application
Logique et mathématique
Je laisse ici de côté les questions proprement de logique : logique mathématique / logique musicale.
Cf. mathématiques ≠ logique. Mathématiques naissent avec axiomes d’existence. Logique = tautologies.
Trois modalités
Métaphore
Rapport (« comme ») entre deux termes :
K º C
· Exemple
L’audition musicale est comme une intégration mathématique.
Analogie
Rapport (« comme ») entre deux rapports :
|
a |
º |
b |
|
|
x |
y |
|
|
· Exemple
En musique, le rapport de l’audition au temps musical est comme, en mathématiques, le rapport d’une intégrale à son paramètre :
|
audition |
º |
intégration |
|
|
temps t |
paramètre x |
|
|
Fiction
Faire « comme si » une théorie mathématique pouvait s’interpréter dans un domaine musical inattendu.
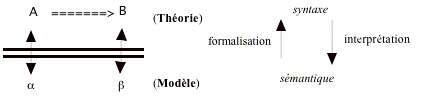

· Exemple
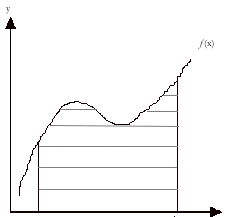
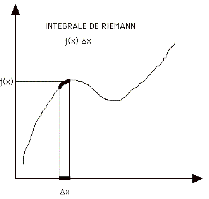
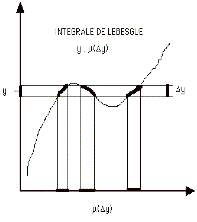
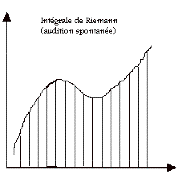
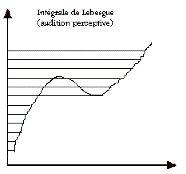
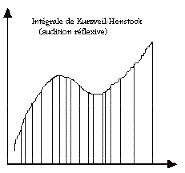
Faire comme si la théorie mathématique de l’intégration pouvait rendre compte de l’audition musicale.
ça marche pas mal !
Intégrales Riemann / Lebesgue / Kurtsweil-Henstock