Comment évaluer musicalement
les théories mathématiques de la musique ?
L’exemple de la théorie de
Mazzola
Séminaire Musique et Mathématiques
(Ens, 16 avril 2005)
François Nicolas
Résumé
On rappellera qu’une certaine mathématique joue un rôle nécessaire dans l’intellectualité musicale. On distinguera à ce titre deux affinités électives (partages d’écriture et de souci logique) et une raisonance privilégiée (le musicien est à l’école de la mathématique en matière de théorisation) parmi les différentes manières musiciennes de se mettre à l’écoute de la mathématique.
On interrogera alors la situation singulière où le musicien est confronté à des théories mathématiques de la musique : comment évaluer musicalement de telles théories, en particulier ces théories mathématiques qui formalisent des théories musiciennes « naïves » ?
Même si le musicien, contrairement au mathématicien, soutient que théories musiciennes et mathématiques ne commutent pas, une théorie mathématique de la musique peut stimuler le musicien, entre autres par des extensions humoristiques et des intensions ironiques.
On examinera sous cesdifférents angles la théorie mathématique de G. Mazzola — The Topos of Music —, tout spécialement ses théorisations du contrepoint, de la modulation et du geste.
On conclura sur l’intérêt pour le musicien pensif d’une singulière figure subjective de mathématicien qu’on proposera de nommer intellectualité mathématique et dont on esquissera les principales caractéristiques.
Enregistrement : http://www.diffusion.ens.fr/index.php?res=conf&idconf=642
Plan
I. Le rôle nécessaire d'une
certaine mathématique dans l'intellectualité musicale.................. 2
I.1. Trois
sortes de raisonances.............................................................................................. 2
I.2. Rapports
non symétriques................................................................................................ 2
· Remarque..................................................................................................................... 2
I.3. Les
affinités électives entre pensée musicale et pensée mathématique.............................. 2
I.3.a Nombres et
figures ?................................................................................................... 2
· Nombres....................................................................................................................... 2
· Figures......................................................................................................................... 2
I.3.b Écriture et logique !.................................................................................................... 2
· Écritures....................................................................................................................... 2
· Logiques....................................................................................................................... 2
· Deux vulgarisations...................................................................................................... 3
· Égalité de pensée.......................................................................................................... 3
I.4. La
raisonance privilégiée par intellectualité musicale...................................................... 3
I.4.a Rappels....................................................................................................................... 3
· Intellectualité
musicale................................................................................................. 3
· Trois dimensions........................................................................................................... 3
I.4.b Le principe du contemporain...................................................................................... 3
· Deux exemples.............................................................................................................. 4
I.4.c Se mettre à l’école
de la manière mathématique de théoriser....................................... 4
I.5. Autres
raisonances possibles avec les mathématiques....................................................... 4
I.5.a I. Les deux affinités
électives...................................................................................... 4
· Écritures....................................................................................................................... 4
· Logiques....................................................................................................................... 4
I.5.b II. La raisonance privilégiée....................................................................................... 4
· Ce que veut dire
théoriser............................................................................................. 4
I.5.c III. Les autres raisonances possibles............................................................................ 4
· Penser la musique avec
les mathématiques.................................................................... 4
I.6. Au total............................................................................................................................ 4
II. Un problème particulier....................................................................................................... 4
II.1. Rappel : différents types de théories musicales................................................................. 4
II.1.a Différentes
types......................................................................................................... 4
II.1.b Différents
sens de « théorie de la musique »................................................................ 4
· « La
musique » ne voudra pas dire la même « chose ».................................................. 4
· « Théorie »
ne voudra pas dire la même « chose »........................................................ 4
· ni non plus
« de »......................................................................................................... 5
II.1.c Remarque
sur la dissymétrie........................................................................................ 5
II.2. Premier éclairage – Un étagement non commutatif de théories....................................... 5
II.2.a Théorie
d’un modèle.................................................................................................. 5
II.2.b Théorie
formelle d’une théorie naïve.......................................................................... 5
· Premier résultat,
première question............................................................................... 5
II.2.c Un
pas de plus : non-commutativité............................................................................ 5
· Détaillons….................................................................................................................. 5
· Objection et réponse..................................................................................................... 5
· Revenons à nos deux
subjectivités................................................................................. 5
II.3. Deux stimulations pour le musicien................................................................................. 6
II.3.a Les
extensions humoristiques...................................................................................... 6
· Remarque..................................................................................................................... 6
· Exemples ?................................................................................................................... 6
II.3.b Des
intensions ironiques ?........................................................................................... 6
· Exemples ?................................................................................................................... 6
II.3.c Évaluation
musicienne du caractère fructueux de la théorie........................................ 6
III. La théorie mathématicienne de la musique
par Mazzola..................................................... 6
III.1. Théorie mathématique et pas seulement mathématisée.................................................... 6
III.1.a Une
théorie mathématisée de la musique..................................................................... 6
III.1.b Une
théorie mathématique de la musique.................................................................... 6
III.1.c Triplet
objet-logique-stratégie..................................................................................... 6
III.2. Théorie mathématique de théories musiciennes naïves..................................................... 7
III.2.a Isomorphisme
Riemann-Fux....................................................................................... 7
III.2.b Intérêt
pour le musicien ?............................................................................................ 7
III.3. Quatre exemples.............................................................................................................. 7
III.3.a La
formalisation mathématique des fonctions harmoniques......................................... 7
· Pourquoi alors
privilégier la bande de Möbius plutôt que le cylindre ?........................ 7
III.3.b La
formalisation mathématique du contrepoint........................................................... 7
III.3.c La
formalisation mathématique de la modulation........................................................ 8
· Cadence....................................................................................................................... 8
· Modulation................................................................................................................... 8
· Intérêt pour le
musicien ?............................................................................................. 8
III.3.d La
formalisation mathématique du geste..................................................................... 8
· Commutativité
mathématicienne.................................................................................... 8
· Non-commutativité
musicienne...................................................................................... 9
III.4. Thèse : la musique est intrinsèquement non-commutative.............................................. 10
IV. Une nouvelle figure de mathématicien et
des raisonances d’un type nouveau................... 10
IV.1. Une intellectualité mathématique................................................................................... 10
IV.1.a Caractéristiques......................................................................................................... 10
IV.1.b Antécédents ?............................................................................................................ 10
IV.1.c Analogies
avec intellectualité musicale ?................................................................... 10
IV.2. Raisonances entre intellectualités musicale et mathématique ?...................................... 10
IV.3. Deux compréhensions duales de la musique.................................................................. 10
I. Le rôle nécessaire d'une certaine mathématique dans l'intellectualité musicale
I.1. Trois sortes de raisonances
Il y a trois sortes de raisonances entre musique et mathématiques :
1) deux affinités « électives » entre pensée musicale et pensée mathématique ;
2) une raisonance privilégiée par l’intellectualité musicale se mettant à l’école de la pensée mathématique ;
3) d’autres raisonances possibles, pour « penser la musique avec les mathématiques » (c’est-à-dire quand l’intellectualité musicale se met à l’écoute de la pensée mathématique).
I.2. Rapports non symétriques
Noter : ces rapports ne sont pas symétriques. Je traite ici des raisonances de la mathématique avec la musique, c’est-à-dire des rapports où les mathématiques font vibrer la musique, et je laisse aux mathématiciens (cf. le thème de cette année : les mathématiciens et la musique) le soin de déterminer la capacité éventuelle de la musique de faire vibrer les mathématiques…
· Remarque
Cf. cette remarque, d’évidence, mais frappante : il n’existe pas de théorie musicale de la mathématique. Peut-il en exister une ? Est-ce l’ouverture de ce nouveau chantier que Guerino Mazzola va nous annoncer aujourd’hui ?
I.3. Les affinités électives entre pensée musicale et pensée mathématique
À quoi tiennent-elles ?
I.3.a Nombres et figures ?
On pose souvent que ces affinités tiennent aux nombres et aux figures, c’est-à-dire à ce qui constituerait les deux objets mathématiques par excellence.
· Nombres
Cf. Pythagore.
D’où une arithmétisation de la musique qui faisait l’admiration du théologien. Rappelons-nous St Thomas donnant à la théologie la musique pour modèle en raison de sa docilité devant l’arithmétique :
« La doctrine sacrée est une science. Mais, parmi les sciences, il en est de deux espèces. Certaines s’appuient sur des principes connus par la lumière naturelle de l’intelligence : telles l’arithmétique, la géométrie et autres semblables. D’autres procèdent de principes qui sont connus à la lumière d’une science supérieure : comme la perspective de principes reconnus en géométrie, et la musique de principes qu’établit l’arithmétique. Or, c’est de cette dernière façon [hoc modo] que la théologie est une science. Elle procède en effet de principes connus à la lumière d’une science supérieure, qui n’est autre ici que la science même de Dieu et des bienheureux. Et comme la musique s’en remet aux principes qui lui sont livrés par l’arithmétique, ainsi la doctrine sacrée accorde foi aux principes révélés par Dieu. » [1]
— Leçon ?
Quand les nombres et l’arithmétique font la mathématique, la musique est subalternée à la mathématique.
· Figures
Cf. Descartes : Compendium Musicæ (1618)
Rappel : Descartes est parti d’un étonnement philosophique devant le fait que l’ordre musical des consonances ne suivait pas (plus ?) l’ordre arithmétique des nombres entiers. Ainsi la tierce supplantait la quarte dans l’ordre des consonances (après l’unisson, l’octave et la quinte). Or l’intervalle de tierce est attaché au nombre 5/4 quand l’intervalle de quarte l’est au nombre 4/3 (la quinte à 3/2 et l’octave à 2/1). Ainsi il est légitime de mettre en parallèle les deux séries de nombres et d’intervalles suivantes :
1 |
Unisson |
1/1 |
|
2 |
Octave |
2/1 |
|
3 |
Quinte |
3/2 |
|
|
Quarte |
4/3 |
|
5 |
Tierce majeure (do-mi) |
5/4 |
|
6 |
tierce mineure (mi-sol) |
6/5 |
|
7 |
petite tierce mineure
(sol-si b) |
7/6 |
|
8 |
Grande seconde majeure (si
b – do) |
8/7 |
|
9 |
Seconde majeure (do-ré) |
9/8 |
|
10 |
petite seconde majeure
(ré-mi) |
10/9 |
|
… |
… |
… |
|
16 |
seconde mineure (si-do) |
16/15 |
La quarte précédait la tierce jusqu’au XII° siècle, respectant ainsi l’ordre arithmétique. Or à partir du XIII°, la tierce est passée devant la quarte, tordant ainsi l’ordre numérique et affirmant une autonomie des lois musicales par rapport aux lois arithmétiques.
Pour Descartes, ceci est un évènement qui doit mobiliser la philosophie.
Pour rendre raison philosophique à ce nouvel ordre musical, Descartes va déployer un jeu de figures, en réévaluant les résonances du point du partage du monocorde :
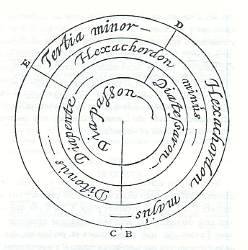
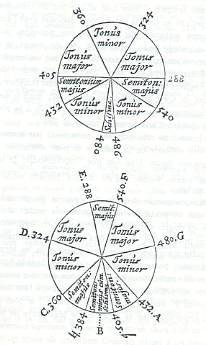
Il va, à partir de là, être amené à dualiser l’espace du monocorde, et ainsi à métaphoriser spatialement un partage entre certitude et doute. [2]
— Leçon ?
Quand les figures et la géométrie font la mathématique, la musique n’est plus subalterne à la mathématique mais à la physique mathématisée.
I.3.b Écriture et logique !
Ma position s’oppose à ces deux types d’explication. Je tiens que la mathématique ne se caractérise pas par des objets particuliers (et donc pas plus par les nombres que par les figures [3], mais par la nature ontologique de sa pensée.
Je pose que les affinités électives de la musique avec les mathématiques tiennent non à des objets particuliers mais à un double partage en matière de mode de pensée :
1) un partage d’écriture, c’est-à-dire d’une manière de penser à la lettre ;
2) un partage de souci logique.
Je tiens alors que ces affinités ne disposent nullement la musique en position subalterne par rapport à la mathématique ou à d’autres sciences, mais en égalité de pensées.
· Écritures
Il y a un partage d’écriture entre musique et mathématiques.
La musique est le seul art à s’être doté d’une écriture (solfège) propre. Cf. rôle considérable de cela pour doter la musique d’une consistance de monde [4]. Cf. élément moteur pour étonner Descartes et par là impulser sa philosophie ; son Abrégé de musique est ainsi constellé d’exemples musicaux tel celui-ci :

De même l’écriture mathématique est l’écriture des sciences, de la physique en particulier qui n’a pas d’écriture propre…
— Remarque
Il faut en ce point différencier matériau et matière : la musique a rapport privilégié à la physique de part le caractère acoustique de son matériau (et aussi de part les corps qu’elle met en jeu) mais la pensée musicale entre en raisonance avec la pensée mathématique de part sa matière proprement littérale : les deux pensent « à la lettre ».
· Logiques
Il y a un souci logique en partage entre musique et mathématiques.
La logique musicale n’est pas isomorphe à la logique mathématique. Par bien des aspects, on pourrait soutenir qu’elle lui est orthogonale, au niveau en tous les cas des grands principes logiques : identité, contradiction, tiers-exclus.

Le souci logique commun se matérialise ainsi en un partage de la déduction (partage désignant ici à la fois le commun et la séparation) qui donne d’un côté le développement musical, de l’autre la démonstration mathématique.
— Trois instances logiques en musique…
Plus généralement, la logique en musique tresse trois instances, non une seule :
— L’écriture comme instance logique du monde de la musique : c’est elle qui conditionne formellement la cohérence de ce monde singulier. Elle occupe à mon sens la position du classifieur de sous-objets W dans le topos de la musique…
— La dialectique comme instance logique des pièces de musique : c’est elle qui conditionne formellement la consistance d’une pièce, la possibilité de son unité — voir la « logique musicale » au sens plus étroit présenté ci-dessus : celle du développement… —.
— La stratégie comme instance logique d’une œuvre singulière : c’est elle qui conditionne formellement l’insistance de cette œuvre, la possibilité qu’elle soutienne un projet musical propre d’un bout à l’autre de la pièce de musique qu’elle est également.
La logique en musique opère ainsi à la fois
· comme
cohérence d’écriture du monde,
· comme
consistance dialectique des pièces,
· comme insistance stratégique de chaque œuvre.
· Deux vulgarisations
Le partage d’écriture et de souci logique entre musique et mathématiques se vérifie en ceci qu’elles partagent également les mêmes modes de vulgarisation, si l’on définit la vulgarisation comme une manière de présenter des résultats musicaux ou mathématiques en faisant l’économie de leur structure écrite comme de leur déploiement logique :

· Égalité de pensée
Au titre de ces affinités électives, en matière donc de partage d’écritures et de soucis logiques, la musique n’est pas subalterne de la mathématique ; mieux : musique et mathématique sont à égalité de pensée.
I.4. La raisonance privilégiée par intellectualité musicale
Elle touche à la dimension proprement théorique de l’intellectualité musicale.
I.4.a Rappels
· Intellectualité musicale
C’est le travail spécifique du musicien pensif (différent du musicien-artisan et du musicien anti-intellectualité musicale) pour dire la musique qu’il fait.
Les différences entre ces trois types de musiciens se font sur une base subjective. Elles ne concernent pas directement leurs œuvres musicales.
L’intellectualité musicale naît très précisément après 1750 (grand tournant dans l’histoire de la musique, une fois la tonalité musicalement fondée, par un double geste théorique et compositionnel : la même année, 1722 : Traité de l’harmonie de Rameau et Clavier bien tempéré – premier livre - de Jean-Sébastien Bach) à l’occasion de la Querelle des Bouffons (à partir de 1752) : c’est Rameau qui, le premier, l’engage.
· Trois dimensions
Je distingue trois dimensions dans l’intellectualité musicale :
· critique des œuvres musicales
· théorie de la consistance musicale (de ses lois) : « monde de la musique », ou « langage musical »
· esthétique de son époque (du contemporain, de l’esprit du temps).
Plus précisément, ces dimensions peuvent être nommées comme
· généalogie critique des œuvres,
· archéologie théorique du monde (ou langage) musical,
· historicité esthétique de l’époque.
Ces trois dimensions peuvent être représentées comme un triangle :

mieux, comme un trièdre :

mieux encore comme un nœud borroméen :

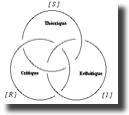
L’intellectualité musicale de Boulez est l’emblème du pôle critique, celle de Rameau du Pôle théorique, celle de Wagner du pôle esthétique et celle de Schoenberg occupe plutôt le centre de gravité général des intellectualités musicales :

I.4.b Le principe du contemporain
Un des trois manières de nouer
ce nœud, celle où l’esthétique noue critique et théorique, concerne ce que
j’appelle le principe du contemporain et qui énonce ceci : pour qu’une
théorie de la musique contemporaine soit musicienne [5],
il lui faut être une théorie contemporaine. C’est-à-dire qu’on ne peut
théoriser la musique contemporaine de manière pertinente pour une
intellectualité musicale que si la manière de
théoriser est elle-même contemporaine.

Le
« contemporain » indexe ici ce que j’appelle esthétique c’est-à-dire la contemporanéité instaurée par une
époque de la pensée.
· Deux exemples
·
Pour Rameau, une théorie
de la nouvelle musique tonale doit être une théorie cartésienne de la musique.
·
Pour Boulez, une théorie
du nouveau langage musical sériel doit être une théorie axiomatisée et
formalisée de la musique.
I.4.c Se mettre à l’école de la manière mathématique de théoriser
Cette
dimension théorique de l’intellectualité musicale instaure à ce titre une raisonance privilégiée avec les mathématiques car la
mathématique peut servir au musicien pensif de modèle en matière de
théorisation. Il s’agit pour le musicien moins de prendre appui sur une théorie
mathématique donnée (la théorie de l’intégration par exemple) que sur une manière
mathématique de théoriser. Bref, l’appui relève plus ici de la logique
mathématique que de la mathématique proprement dite.
Pour
situer cette raisonance dans son
contexte, je soutiens qu’il y a trois raisonances
privilégiées de l’intellectualité musicale, liées à ses trois dimensions :
la poésie (pour la critique), la mathématique (pour le théorique) et la
philosophie (pour l’esthétique).

I.5. Autres raisonances possibles avec les mathématiques
C’est ce que j’appellerai « penser la musique avec les mathématiques » ou mettre l’intellectualité musicale à l’écoute de la pensée mathématique (elle est à l’école proprement dite pour ce qui concerne la théorisation).
Cf.
la liste de dix-sept thèmes, donnée en février, que je reclasserai et trierai
ainsi :
I.5.a I. Les deux affinités électives
· Écritures
8. Penser l’écriture et la lettre musicales avec l’écriture et la lettre mathématiques
· Logiques
1. Penser la logique musicale (et donc l’articulation raison/calcul) avec la logique mathématique
14. Penser le style diagonal de pensée avec la procédure diagonale de Cantor
I.5.b II. La raisonance privilégiée
· Ce que veut dire théoriser
2. Penser le « avec » avec la théorie des modèles
10. Penser le monde de la musique avec la théorie des topos
I.5.c III. Les autres raisonances possibles
· Penser la musique avec les
mathématiques
3. Penser la perception musicale avec la théorie des pavages
4. Penser l’audition avec la théorie de l’intégration
5. Penser l’écoute musicale avec la théorie de la différenciation
6. Penser l’écoute à l’œuvre avec les jeux mathématiques de taquins
7. Penser les modalités de l’entendre avec les théories mathématiques de l’intrinsèque et de l’extrinsèque
9. Penser l’articulation musicale entre écriture et écoute avec l’articulation mathématique (de la théorie) des ensembles et (de la théorie) des catégories
11. Penser la composition musicale avec les théories mathématiques du local et du global
12. Penser l’entre-œuvres des concerts avec la théorie des catégories
13. Penser la combinatoire musicale avec l’algèbre
15. Penser le temps musical avec la théorie des équations différentielles (cf. A. Lautman)
16. Penser la nature musicale avec la théorie des ordinaux et cardinaux (cf. A. Badiou)
17. Penser les rapports de l’œuvre à son matériau avec la théorie des nombres surréels (cf. A. Badiou)
I.6. Au total
|
Raisonances |
Elles
portent sur |
|
Elles
rapprochent : |
|
deux
affinités électives |
écritures & soucis logiques |
Mêmes
types de matières (littérales) ou manières de penser (« à la
lettre ») Mêmes
soucis des formes (logiques) de la pensée |
pensées
musicale & mathématique |
|
une
raisonance privilégiée |
ce
que veut dire théoriser |
L’intellectualité musicale se met « à l’école » de la pensée mathématique |
intellectualité
musicale (pensée musicienne) &
pensée mathématique |
|
autres
raisonances possibles |
[
divers ] |
L’intellectualité
musicale se met « à l’écoute »
de la pensée mathématique |
II. Un problème particulier
Que
se passe-t-il maintenant pour le musicien pensif quand les mathématiques se présentent
sous cette forme singulière d’une théorie mathématique… de la musique ?
Ou
encore : qu’est-ce que le musicien pensif peut penser pour son compte
subjectif propre avec une théorie
mathématique de la musique ?
Mon
hypothèse est que le musicien pensif (celui qui déploie une intellectualité
musicale) se trouve ici proprement encombré d’une telle théorie mathématique de
la musique, ne sachant pas plus en faire qu’un sauvage ne le sait le faire
d’une caméra…
II.1. Rappel : différents types de théories musicales
II.1.a Différentes types
« Théorie musicale », c’est-à-dire « théorie de la musique » se dit en différents sens, si bien qu’il y a différents types de théorie musicale :

Dans le cas précis de l’intellectualité musicale, je parlerai plutôt de dimension théorique que de théorie proprement dite.
Ex. Boulez : il y a sens à parler de la dimension théorique de sa pensée plutôt qu’à proprement parler de sa théorie musicale (qui reste inaboutie, indéfiniment avortée en 1963…).
II.1.b Différents sens de « théorie de la musique »
Dans
chaque cas, « théorie de la musique » ne voudra pas dire la même
chose car
· « La musique » ne voudra pas dire la même
« chose »
Le
plus souvent, une théorie mathématique de la musique est une théorie non des
œuvres musicales mais de telle ou telle structure musicale : échelle (cf. Broué), tempérament (cf. Hellegourach), canons (cf. Andreatta). Ici la musique est essentiellement
un squelette et une tuyauterie… C’est aussi pour cela que Boulez parle du
mathématicien comme occupant pour le musicien la place… du plombier :
« Ne comprenant pas exactement ce que les musiciens réclament d’eux, ne voyant pas quel serait le possible terrain d’efforts communs, bien des scientifiques se récusent à l’avance, ne considérant que l’absurde de la situation : en somme, un mage étant réduit à quémander les services d’un plombier ! Si, de surcroît, le mage estime que lui suffisent les services du plombier, la confusion est totale. » (Leçons de musique, 1976, p. 62)
Pour
l’intellectualité musicale, une théorie musicale doit être, pour des raisons
essentielles, normée par les œuvres, lesquelles sont à la fois la base et le
sommet du monde de la musique. La musique, donc, a ici pour cœur et poumons les
œuvres. C’est pour cela que, du point d’une intellectualité musicale, théorique
et critique doivent être noués (et qu’elles le sont par l’esthétique…).
· « Théorie » ne voudra pas dire la même
« chose »
Exemple : les théories musiciennes se présentent pour la logique contemporaine comme théories « naïves » (ni axiomatisées ni formalisées) et se distinguent de théories « formelles » et ce même si la théorie musicienne s’est mise, comme dans le cas de Boulez, à l’école de la théorisation mathématique.
· ni non plus « de »
Exemple :
pour une théorie mathématique de la musique, la particule « de »
désigne le rapport à un objet. C’est un génitif objectif : une mathématisation
de la musique, c’est une extension ou une application de la pensée mathématique
sur la musique.
Pour
une théorie musicienne de la musique, le même génitif est essentiellement en
intériorité et de type subjectif :
il s’agit toujours, peu ou prou, d’une manière pour la musique de se théoriser via le musicien, de se ressaisir théoriquement par l’intermédiaire du
musicien.
II.1.c Remarque sur la dissymétrie
Existe-t-il
une théorie musicale de la mathématique ?! Pas à ma connaissance ! Ce
qui relève, une fois de plus, la dissymétrie fondamentale des rapports entre musique
et mathématiques, dissymétrie dont il n’y aurait pas de sens à se plaindre ;
ni d’ailleurs à s’en réjouir : la pensée et l’intellectualité musicales ne
sont ici ni victimes des mathématiques ( !) ni volontairement serviles à
leur égard.
*
Comment
s’approprier musicalement une telle théorie mathématique de la musique ?
Cela
n’a rien d’évident : d’ailleurs les musiciens ne se précipitent guère pour
se l’approprier…
D’où
mes nombreuses discussions avec Guerino Mazzola, en particulier sur ce que veut
dire « musique » en toute cette affaire, aussi bien pour le dire musicien (ses leçons) que pour le faire musicien (son concert free jazz…). Comment le musicien se repère-t-il dans ce grand
écart entre une théorie de la musique à la lettre mathématique
et une pratique de la musique attachée au corps du musicien ? Comment
l’intellectualité musicale peut-elle s’orienter face à une musique saisie dans
une très étrange pince : celle
· de la lettre mathématique (où le diagramme mathématique remplace la partition musicale),
· d’un corps physiologique (où le geste du musicien remplace la trace sonore du corps à corps [6]).
II.2. Premier éclairage – Un étagement non commutatif de théories
Pour
m’« orienter dans la pensée », je propose de formaliser — de
« diagrammatiser » — ainsi ce qui à mes yeux constitue un
problème (mais n’en constitue sans doute pas un aux yeux de Guerino Mazzola).
II.2.a Théorie d’un modèle
Diagrammatisons cela ainsi :

Rappel :
un intérêt capital de la théorie est ici de produire des enchaînements
déductifs (entre A et B) là où le modèle (musical) n’en comporte pas : il
y a au mieux des successions, mais pas de déductions explicites dans le modèle.
Le
modèle musical est constitué d’un champ de « choses » plus ou moins
structuré : des objets harmoniques, ou rythmiques, ou instrumentaux…
II.2.b Théorie formelle d’une théorie naïve
En
général, une théorie mathématique de la musique va s’édifier en prenant pour
modèle un champ musical déjà structuré selon ce qu’on appellera une théorie
musicienne « naïve ». D’où le schème étagé suivant :

qui,
dans notre situation, signifie ceci :

Ainsi l’intellectualité musicale du musicien transforme un développement musical en déduction musicienne, et la théorie mathématique transforme cette déduction musicienne « naïve » en démonstration.
· Premier résultat, première question
Premier résultat : le musicien, réfléchissant sur les œuvres et leurs développements, bâtit des déductions (voir la place décisive de cette catégorie dans l’intellectualité musicale de Boulez). Le mathématicien, lui, réfléchissant sur les développements musicaux et les déductions musiciennes, bâtit des démonstrations mathématiques.
Le mathématicien offre ainsi au musicien pensif une nouvelle manière de circuler de a à b et même de a à ß. Comment le musicien va-t-il pouvoir se rapporter à ces nouvelles flèches ? Vont-elles constituer pour lui de nouvelles déductions ?
II.2.c Un pas de plus : non-commutativité
Pour examiner cela, enrichissons et simplifions notre diagramme :


P et Q ne désignent pas ici les flèches composées F°f et g°G mais les éventuelles formalisations mathématiques directes (c’est-à-dire ne passant pas la théorie naïve) des choses musicales a et ß.
La théorie mathématique construit donc une nouvelle flèche G°D°F entre a et b. Appelons-la un déploiement.
Que faire musicalement d’un tel déploiement ?
Ma thèse fondamentale est la suivante : pour le musicien, ce diagramme ne commute pas alors que le désir du mathématicien est par contre que ce diagramme commute. D’où une première très forte dissonance entre désirs musicien et mathématicien.
Ce discord s’écrira précisément ainsi :
La thèse musicienne sera que déduction musicienne [d] et interprétation°démonstration°formalisation mathématiques [G°D°F] ne commutent pas.
· Détaillons…
Qu’en est-il pour l’éventuelle commutation du reste du diagramme ?
— g°d°f / g°G°D°F°f ?
Formellement, si f est un épimorphisme et g un monomorphisme, on peut déduire de d≠G°D°F que g°d°f≠g°G°D°F°f.
Qu’est-ce que cela veut dire ? Que même si déduction musicienne et démonstration-déploiement mathématiques conduisent bien au même objet musical ß, leurs « logiques » (le sens de l’enchaînement qu’elles conçoivent) restent cependant de natures différentes.
— g°d°f / Q°D°P ?
Il y a ici encore moins de raison pour que ces deux flèches composées soient identiques et que les logiques ou sens des enchaînements soient isomorphes.
· Objection et réponse
On peut objecter que la commutativité catégorielle concerne des diagrammes où deux couples de morphismes convergent sur le même objet :
donc  plutôt que
plutôt que 
Je soutiendrai que le digramme déduit des précédents par « interprétation » de A en a (et non plus par « formalisation » de a en A) ne commute pas:

Le point de partage se concentre en effet sur l’hétérogénéité radicale des « morphismes » d et D qui interdit qu’ils puissent commuter.
· Revenons à nos deux subjectivités
Le désir mathématicien est tout au contraire que le diagramme précédent commute.
Tendons un peu plus le partage des subjectivités :
· l’intérêt pour un musicien d’un tel diagramme est qu’il ne commute pas ;
· à l’inverse, ce qui intéresse un mathématicien dans un tel diagramme, c’est sa part qui commute ou peut commuter. Pour cela, le mathématicien va faire « comme si » les différentes flèches étaient composables, donc « comme si » les différences de « nature » entre flèches pouvaient s’éponger par composition commutative.
J’oppose à cela la thèse que, par-delà leurs affinités naturelles, par-delà affinités et raisonances diverses, musique et mathématique à proprement parler ne composent pas, sont incomposables.
II.3. Deux stimulations pour le musicien
II.3.a Les extensions humoristiques
L’intérêt pour le musicien d’une telle théorie mathématicienne va tenir à tout autre chose qu’à une pseudo-commutativité. Elle va tenir à la capacité de cette théorie mathématique de générer de nouvelles structures musicales, mathématiquement isomorphes et musicalement hétéromorphes.
Cf.

Ici, tout l’intérêt de la théorie mathématique tient pour le musicien non plus à une commutativité mais à la nature de l’objet musical g ainsi mathématiquement engendré.
La question pour le musicien va alors prendre la forme suivante :

Soit : comment évaluer musicalement le rapport inattendu déployé par les mathématiques entre g et ß (via un rapport entre c et b) ? À quel titre musical g « développe »-t-il ß ? Puis-je théoriser ce développement musical par une « déduction » musicienne d’ entre c et b ?
L’évaluation musicienne de la théorie mathématique va donc se faire au niveau des résultats : par évaluation de la qualité musicale des extensions proposées par la théorie en question.
Ici la mathématique fournit l’occasion de rapprochements musicaux inattendus. Appelons cela la dimension proprement humoristique (pour le musicien) des théories mathématiques de la musique puisqu’il s’agit de rapprocher des lointains.
· Remarque
Guerino thématise cela mathématiquement comme explicitation de la fibre (à gauche) créatrice d’un voisinage (à droite) d’un point-image a(a) :
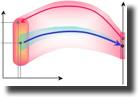

· Exemples ?
On va trouver de nombreux exemples de telles extensions humoristiques dans la théorie mazzolienne.
II.3.b Des intensions ironiques ?
D’où immédiatement la question duale : y aurait-il de même pour le musicien une dimension ironique des théories mathématiques de la musique qui cette fois éloigne les proches, qui instaure une distance de pensée au plus près? Bref, au lieu d’extensions humoristiques, les théories mathématiques de la musique peuvent-elles fournir au musicien des intensions ironiques ?
Que serait-ce formellement ?
La situation de départ du musicien serait cette fois celle-ci :

celle d’une égale proximité de ß à a et g.
L’intervention de la théorie mathématique aurait désormais pour effet de déployer un espace intérieur entre ß et g, en sorte de révéler une distance au lieu même d’une apparente proximité :

Pour le musicien, il s’avèrerait donc que la proximité entre ß et g n’est peut-être pas celle qu’il pensait, qu’en fait g ne suit pas ß comme ß suit a, bref que le développement a sauté inopinément des étapes et que la véritable déduction musicienne devrait concevoir c comme étant quatre fois plus loin de b que jusque-là considéré.
D’où une intension ironique.
· Exemples ?
La théorie mazzolienne de la cadence à mon sens suggère cette direction…
II.3.c Évaluation musicienne du caractère fructueux de la théorie
Dans les deux cas — extension humoristique et intension ironique — le musicien évalue la théorie mathématique au regard de ses fruits musicaux pour lui musicien.
III. La théorie mathématicienne de la musique par Mazzola
III.1. Théorie mathématique et pas seulement mathématisée
Donnons de tout ceci des exemples concrets à partir de la théorie mazzolienne de la musique, théorie qui relève clairement du type mathématique (plutôt que musicien) des théories musicales.
Un symptôme très patent du caractère proprement mathématicien de cette théorie est qu’elle ne vise pas qu’à éclairer la musique mais également à développer les mathématiques pour elles-mêmes. Les mathématiques, dans cette théorie, se déploient en-soi et pas seulement « pour la musique ». Ceci est tout à l’honneur mathématique de ce travail mais crée des difficultés supplémentaires pour le musicien qui s’y intéresse.
Précisons : il s’agit bien ici d’une théorie mathématique de la musique et pas simplement d’une théorie mathématisée.
III.1.a Une théorie mathématisée de la musique
Une théorie mathématisée de la musique est une théorie de la musique qui est mathématiquement formalisée, comme il existe par exemple des théories mathématisées de l’économie, ou de la circulation des trains, etc. Cette formalisation est alors stratégiquement ordonnée aux fins du modèle retenu.
III.1.b Une théorie mathématique de la musique
Une théorie mathématique de la musique est aussi mathématiquement formalisé mais, cette fois, les fins sont pour bonne part proprement mathématiciennes : on part ici du domaine musical pour examiner les problèmes mathématiques qu’il est susceptible de susciter. Il s’agit désormais moins de partir de problèmes musicaux (à résoudre mathématiquement parce qu’on ne saurait pas les résoudre musicalement) que de problématiser mathématiquement des pratiques et théories musiciennes en sorte de générer des problèmes proprement mathématiques.
III.1.c Triplet objet-logique-stratégie
La distinction précédente suggère ainsi qu’il faudrait distinguer les types de théorie, non seulement par leur compréhension propre de « l’objet-musique » mais aussi par leurs visées stratégiques propres : il est clair qu’une théorie sociologique de la musique, par exemple a des visées plus sociologiques que musicales (d’où qu’elle n’apprenne à peu près rien sur les œuvres musicales).
Ainsi une théorie Xienne de la musique se caractériserait par le croisement d’un type Xien de consistance discursive (tenant à la discipline de pensée considérée), d’une caractérisation Xienne de son objet et d’un type Xien de stratégie.
Ou encore : la nature particulière (mathématique, musicienne, sociologique…) d’une théorie musicale se donnerait dans le triplet d’une consistance, d’un objet et d’une stratégie.
III.2. Théorie mathématique de théories musiciennes naïves
Autre trait remarquable : la théorie mathématique de Mazzola formalise des théories musiciennes existantes plutôt que la matière musicale proprement dite.
III.2.a Isomorphisme Riemann-Fux
Ex. Fux et Riemann.
D’où un résultat intéressant — qui intéresse essentiellement la musicologie historique — : les théories de Riemann et Fux sont isomorphes (au titre, non trivial, de leurs dichotomies consonances-dissonances [7]). Cette théorie mathématique unifie ainsi deux types de théories musiciennes selon le diagramme suivant :

La théorisation dégage ici des enchaînements inattendus entre théories naïves. C’est un exemple de ce que j’appelle l’humour mathématique : quand le musicalement lointain est mathématiquement rapproché.
III.2.b Intérêt pour le musicien ?
L’intérêt de tout ceci pour le musicien est de dégager la cohérence sous-jacente de ses théories naïves. Mais il n’y a pas ici de conséquences pratiques immédiates car ces pratiques musicales (du contrepoint et de l’harmonie tonale) sont depuis longtemps obsolètes pour la création artistique.
III.3. Quatre exemples
Prélevons quatre exemples dans cette théorie de Mazzola :
· sa formalisation des fonctions harmoniques,
· sa formalisation du contrepoint,
· sa formalisation de la modulation,
· sa formalisation du geste.
III.3.a La formalisation mathématique des fonctions harmoniques
On a, grâce à une triangulation des fonctions tonales, le ruban suivant :

Rappel : I a deux notes communes avec III et VI, et une note commune avec V et IV.
Mazzola choisit de privilégier de couper ce ruban au milieu et de recoller I-III par une torsion (d’où le ruban de Möbius) [8] :

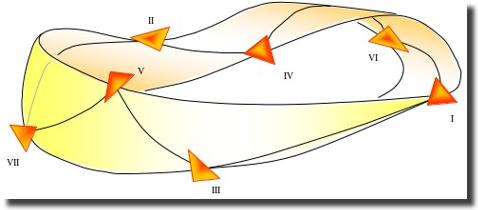
Mais on pourrait tout aussi bien le recoller deux fois plus loin, sans torsion cette fois (on aurait alors un cylindre).

· Pourquoi alors privilégier la bande de Möbius plutôt
que le cylindre ?
Ma compréhension est la suivante.
— La formalisation en bande de Möbius est privilégiée par Mazzola pour des raisons proprement mathématiques : économie formelle de signes [9]. C’est en fait cette économie formelle qui conduit à désorienter la polarité grave/aigu essentielle pour le musicien : elle suppose au départ une indifférence à l’ordre des fonctions harmoniques — elle traitera par exemple les deux fonctions I et V comme un ensemble {I, V} sans distinguer alors I-V de V-I (ce qui d’un point de vue musical est bien sûr tout à fait différent : ouverture/cadence, tension/détente…) —. C’est donc bien parce que cette « orientation » musicale déterminante (selon l’ordre temporel de la succession) est effacée au principe même de la formalisation mathématique retenue que cette formalisation boucle le ruban en bande de Möbius et retrouve ensuite innocemment la propriété globale de désorientation qu’elle a implicitement introduite en son point de départ.
— La formalisation en cylindre rend mieux compte de la réalité harmonique d’un point de vue musical ; le cylindre suggère ainsi, à le parcourir de droite à gauche, l’enchaînement des fonctions suivantes, où l’ordre temporel est évidemment déterminant :

III.3.b La formalisation mathématique du contrepoint
Cf. le tore des tierces [10] :
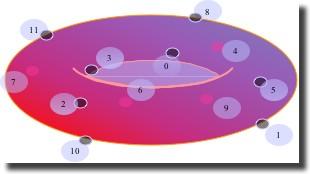
Cf. les dichotomies consonances-dissonances : K={0, 3, 4, 7, 8, 9} et D={1, 2, 5, 6, 10, 11} :
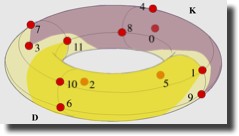
La théorie mazzolienne du contrepoint (plus exactement de la théorie fuxienne du contrepoint) me semble plus fructueuse musicalement que la théorie mazzolienne de l’harmonie (c’est-à-dire de la théorie riemanienne de l’harmonie).
Pourquoi ? Parce que dans le cas du contrepoint la logique mathématicienne adoptée s’éloigne moins de la logique musicienne tant en matière d’objet que de stratégie. En effet,
1) la formalisation du contrepoint « respecte » plus l’orientation musicale du grave vers l’aigu (qui est au principe du rapport dissymétrique entre cantus firmus et déchant) :Mazzola part ici [11] d’un intervalle orienté en sorte de correctement formaliser le contrepoint à deux voix (de différencier donc cantus firmus et déchant par une paire ordonnée où les deux termes ne commutent pas…) quand, au contraire, la formalisation mathématique du « ruban harmonique » (en bande de Möbius plutôt qu’en cylindre) impose une désorientation du matériau harmonique (désorientation découlant d’une indifférence à l’ordre successif, au principe pourtant des fonctions harmoniques considérées) ;
2) la stratégie guidant la formalisation du contrepoint semble guidée par deux idées :
— unifier théories musiciennes de l’harmonie et du contrepoint ;
— généraliser les lois musiciennes du contrepoint à d’autres « échelles ».
Ces deux visées stratégiques, quoique mathématiciennes, s’avèrent cependant rester « parallèles » à des visées plus proprement musiciennes.
· La première est un rapprochement humoristique entre théories naïves éloignées.
· La seconde ouvre à la possibilité d’extensions humoristiques du contrepoint :

Quel est alors rapport musical entre les deux contrepoints ?! Où l’on retrouve ce problème, musicalement bien connu : d’un point de vue musical, tout peut se déduire de tout [12], car la déduction musicale n’a pas la rigueur formelle de la démonstration mathématique.
Où la « génétique » et la « poïétique » s’avèrent ici de peu d’intérêt : le chemin qui a permis d’aboutir à B à partir de A n’est pas forcément pertinent pour décrire les rapports entre A et B, comme le montre l’exemple élémentaire suivant (autre manière, au demeurant, de souligner que tout ceci ne commute guère…) :

Où l’on retrouve ce fait que la commutation mathématique (égalité des deux membres de l’équation) ne s’accorde guère à une non-commutation musicienne (les rapports musicaux en deux objets d’une partition ne sont que très vaguement « explicités » par la manière dont le compositeur les a engendrés).
III.3.c La formalisation mathématique de la modulation
Mazzola part de la théorisation (naïve) schoenberguienne des modulations (Harmonielehre, 1911), en trois moments : neutralisation, accord-pivot sur les degrés modulants, confirmation cadencielle [13].
Dans la théorie de Mazzola, une modulation est alors la dotation du diagramme suivant [14] :

où k est une des 5 « cadences » envisageables [15] entre deux tonalités : II-III, II-V, III-IV, IV-V, VII.
· Cadence
La catégorie de cadence est ici très abstraite de sa réalité musicale : une tonalité (majeure) est vue comme une simple échelle diatonique qu’un seul accord (VII° degré) suffit à identifier statiquement. Ici la cadence est une « représentation résumée de la tonalité » [16]. Elle est mathématiquement traitée comme une fonction du type « formule cadentielle = f(tonalité) » [17]. Elle n’est pas traitée dynamiquement mais comme un ensemble dont l’ordre est indifférent : IV-VºV-IV [18].
Or, musicalement, la catégorie de cadence est essentiellement dynamique : si une tonalité est musicalement identifiée par un accord, c’est plutôt par la septième de dominante (V7) que par VII qui, musicalement, est tout au contraire l’accord vague par excellence (septième diminuée).
— Intérêt proprement musical ?
En ce point, il faudrait explorer plus avant cette théorie de la cadence pour en exhausser le potentiel sans doute d’intension ironique…
· Modulation
En conséquence, la catégorie même de modulation est ici assez distante de sa réalité musicale. C’est ce qui aboutira à exhausser mathématiquement, dans l’opus 106 de Beethoven, certaines « modulations » dites « catastrophiques » [19] : G. Mazzola thématise mathématiquement ces « modulations » en les attachant à des « cadences » (au sens toujours mathématique du terme) très particulières.
Où l’on retrouve ce problème récurrent : des mêmes mots — ici « cadence », « modulation » — nomment des choses très différentes dans le cadre d’une théorie musicienne et d’une théorie mathématique de la musique. C’est bien sûr normal, mais cela implique une très grande attention dans l’interprétation ultérieure des énoncés.
On constate alors une différence d’accents significatifs : par exemple, pour l’analyse musicienne du schéma global des tonalités, à la limite peu importe comment Beethoven module de E en A mais pour le mathématicien, ici ce n’est plus le cas puisque l’analyse va distinguer minutieusement modulations « quantiques » et modulations autres.
· Intérêt pour le musicien ?
De nouvelles extensions humoristiques !
Voir ainsi la « démonstration » mathématique qui conduit à la « déduction » musicienne et au « développement » musical suivant :

III.3.d La formalisation mathématique du geste
· Commutativité mathématicienne
Guerino Mazzola privilégie une formalisation (commutative) du geste physiologique du musicien :



Mais de quelle musique s’agit-il exactement ici ?
Quel rapport musical y a-t-il entre la musique mathématiquement formalisée à gauche et la musique improvisée attachée à un corps de musicien à droite ?

Il ne s’agit pas de dresser ici l’objection obscurantiste opposant la mort du formel à la vie du corporel. Il s’agit tout au contraire de ne pas s’enfermer dans une dichotomie où il y aurait d’un côté une structure mathématique, obsessionnellement construite, et de l’autre un corps musicien, hystériquement livré en garant de la musicalité.
À nouveau, l’hypothèse commutative est au principe de cette démarche mathématicienne : il s’agit de formaliser mathématiquement les structures musicales de la partition puis les structures du corps physiologique du musicien pour en déduire ses mouvements aptes à matérialiser l’exécution (et pourquoi pas l’interprétation) de la partition de départ. Au total, la composition de ce parcours doit équivaloir à une flèche directe (celle du bas entre la partition et le corps de Gould dans le diagramme suivant) :

Je remarquerai cependant qu’on n’a pas ici à proprement parler un corps musical c’est-à-dire le corps physique du piano — sa table d’harmonie —vibrant sous l’effet du corps à corps, rayonnant et projettant dans un lieu la trace sonore de ce corps à corps.
Je pose, en effet, que la musique transite par un corps à corps (« corps-accord » [20]) sans s’y attacher car la musique me semble un art de l’écoute plutôt qu’un art du jeu (qu’un art du corps-accord) : la musique procède essentiellement d’une écoute de la trace d’un corps-accord. Si l’on veut formaliser le geste musical en musicien, il nous faudrait donc procéder autrement.
· Non-commutativité musicienne
Concernant le geste, je diagrammatiserai ainsi une conception plus proprement musicienne :

— Remarques
· Le rapport de la partition au corps du musicien n’est pas univoque, fonctionnel, car la partition a pour cœur une écriture musicale qui n’est pas une tablature. La partition ne prescrit donc pas directement un geste du musicien.
· Le jeu musicien consiste à accorder son corps à un corps instrumental situé dans une salle. Le jeu est une opération qui convolue un instrument situé et un musicien.
· Le résultat du jeu est un son rayonné par le corps-accordé dans un lieu architectural.
· On n’écoute pas le corps du musicien. Concernant le corps instrumental, on l’entend certes mais on ne l’écoute pas ; ce que l’on écoute, c’est la trace du corps-accord dans un son situé.
· L’écoute n’est donc écoute ni du musicien, ni de l’instrument, ni du lieu, ni même du jeu mais plutôt de la trace de ce jeu dans un lieu.
· Écouter, c’est déconvoluer en sorte de dégager à l’intérieur du son (musical) la trace (du corps-accordé dans le lieu) et de séparer cette trace du déchet musical. La trace s’affirme par soustraction du déchet.
· Corrolaire : le musicien est le déchet de la musique. La vision de l’auditeur doit aider à déconvoluer la trace du déchet, non conduire à s’attacher unilatéralement au corps du musicien en train de jouer…
— Thèse
Je tiens que dans ce diagramme rien ne commute.
En particulier on a : injection ≠ écoute°adresse°rayonnement !
Plus techniquement, les « convolutions » du diagramme précédant ne sont pas des sommes ou coproduits, et la partition n’y est pas un produit.
On n’a donc pas le diagramme suivant qui schématise le désir mathématicien d’une commutation généralisée :

Détaillons.
—
La partition
Pour un
mathématicien :

Pour un
musicien :
La partition n’est pas produit, limite du diagramme {musicien, instrument}. Le diagramme avec le fichier Midi ne commute pas.
— Le corps-accord
Pour un
mathématicien :

Pour un
musicien :
Le corps-accord n’est pas somme (coproduit), colimite du diagramme {musicien, instrument}. Le diagramme avec Modalys ne commute pas.
— La spatialisation
Pour un
mathématicien :

Pour un
musicien :
La spatialisation n’est pas somme (coproduit), colimite du diagramme {instrument, salle}. Le diagramme avec la WFS ne commute pas.
III.4. Thèse : la musique est intrinsèquement non-commutative
Au total, non seulement musique et mathématiques ne commutent pas mais en musique, il n’y aurait guère de commutation.
Soit la nouvelle thèse radicale suivante : la musique est intrinsèquement non-commutative.
On serait donc bien face à deux types différents d’appréhension du phénomène musical — un type mathématicien et un type musicien — et les opérations propres à chacun de ces types ne composeraient pas ensemble, ne commuteraient pas.
À bien y regarder, si musique et mathématique peuvent d’ailleurs raisonner ensemble (et ce, par-delà les applications bien compréhensibles de l’ontologie à toute ontique), c’est précisément parce qu’elles ne peuvent composer leurs matières mais simplement s’entrechoquer, se frotter l’une à l’autre sans que leurs matières propres se mélangent, se mixent.
IV. Une nouvelle figure de mathématicien et des raisonances d’un type nouveau
IV.1. Une intellectualité mathématique
Je tiendrai, par ailleurs, que Mazzola s’emploie non seulement à établir une théorie mathématique de la musique mais aussi quelque chose que je propose d’appeler une intellectualité mathématique.
IV.1.a Caractéristiques
Une intellectualité mathématique se caractériserait par :
· un souci de thématiser les mathématiques qu’on fait ;
· un souci des raisonances mathématiques avec d’autres pensées (et pas seulement de leurs applications) ;
· la nature même du travail intellectuel : être à la fois plongé dans les mathématiques et en léger surplomb sur les mathématiques, se tenir au bord du travail du mathématicien, à la frontière des mathématiques.
· une manière d’introjecter dans la mathématique la réflexion (ou pensée de la pensée) mathématique, une manière donc de se délimiter à l’écart de l’épistémologie (comme l’intellectualité musicale peut le faire à l’égard de la musicologie ou de l’esthétique académique), une manière de déployer une pensitivité mathématicienne donc.
IV.1.b Antécédents ?
Date de naissance ?
Grandes figures ?
· Henri Poincaré (1854-1912), Hermann Weyl (1885-1955)
· Cas particuliers : les logiciens (Cantor, Gödel…), Grothendieck (intellectualité a posteriori)
· Aujourd’hui : Alain Connes, René Guitart…
IV.1.c Analogies avec intellectualité musicale ?
Trois pôles comme en musique ? Avec la philosophie, avec la musique (& les arts) et avec la physique (& les autres sciences) ?
Je me lance :

Nouage borroméen ?…
IV.2. Raisonances entre intellectualités musicale et mathématique ?
La raisonance avec l’intellectualité mathématique de Mazzola dépasse donc largement l’intérêt musicien pour sa théorie mathématique de la musique.
Cette théorie alimente il est vrai le musicien en nouvelles réflexions, en une nouvelle compréhension des théories musiciennes naïves, en extensions humoristiques, en intensions ironiques, etc. Mais faire entrer en raisonance une intellectualité musicale avec cette intellectualité mathématique n’est pas se cantonner à tout cela : c’est également faire en sorte que ces deux types radicalement différents d’intellectualité se frottent l’une à l’autre, comme on frotte un silex contre un autre, non pour les mélanger mais pour faire jaillir quelques étincelles aptes à alimenter le feu de la pensée.
IV.3. Deux compréhensions duales de la musique
Ainsi se sont implicitement frottées dans cet exposé deux catégories, à la fois très proches et cependant radicalement disjointes : la catégorie mathématique de topos (centrale dans la théorie mazolienne) et la catégorie musicienne de monde (centrale dans ma propre intellectualité musicale). Je soutiens que la musique est un monde à mesure de ce qu’elle est comme un topos (analogie) quand Guerino Mazzola soutient à l’inverse que la musique est un topos, et peut-être m’accorderait-il alors que c’est pour cela que l’on pourrait en dire qu’elle est comme un monde… Plus encore, la musique pour moi est un monde essentiellement non-commutatif quand elle est, pour Mazzola, un topos truffé de commutativités.
D’où la nature très
particulière du dialogue entre musicien et mathématicien pensifs, qui tentent de s’entendre tout en évoluant dans des espaces
duaux et qui, finalement, communiquent par résonances de coups frappés de
l’extérieur sur la membrane enveloppant chacun des deux espaces de pensée.
–––––––