D’une longue marche de la modernité musicale, à la lumière de l’algèbre galoisienne

(séminaire mamuphi, 20 janvier 2018)

(pdf)

[ vidéo ]

François Nicolas

[ Introduction à l’atelier mamuphi sur Galois, le samedi 7 avril 2018 à l’Ircam]

Résumé........................................................................................................................................... 1

Attendus......................................................................................................................................... 4

De l’algèbre en mamuphi …..................................................................................................... 4

D’une singularité algébrique dans la théorie de Galois….................................................. 4

D’une puissance de pensée spécifiquement moderne…...................................................... 5

D’une mutation réussie par la modernité mathématique dans les années 60.................. 6

De trois périodes dans les différentes modernités…............................................................ 6

Un exemple.................................................................................................................................... 7

Une équation............................................................................................................................. 7

Cinq racines inconnues à cependant classer......................................................................... 8

Opérations sur un regroupement défini mais indéterminé................................................ 9

Correspondance de Galois..................................................................................................... 10

Alliage de six gestes galoisiens de pensée............................................................................... 11

1. Rédupliquer............................................................................................................................ 11

2. Renverser................................................................................................................................ 11

3. Dualiser.................................................................................................................................. 12

4. Étendre................................................................................................................................... 12

5. Adjoindre............................................................................................................................... 12

6. Renoncer................................................................................................................................ 12

Un alliage................................................................................................................................. 12

Annexes........................................................................................................................................ 13

D’une mélancolie mathématicienne précédant l’événement-Galois................................ 13

D’un nécessaire renoncement…........................................................................................... 13

Douze moments mathématiques où ce qui fut soustrait se convertit en affirmation.... 14

Résumé

Les mathématiques modernes naissent autour de 1830 avec la théorie de Galois [1], qui révolutionne l’algèbre en repensant l’équation polynomiale comme correspondance entre corps (de résolution) et groupes (de permutations) de ses racines. Ce faisant, Galois résout une crise algébrique des équations irréductibles (qui, par bien des points, s’apparentait à l’antique crise arithmétique des nombres irrationnels [2]) et arrache ainsi les mathématiques [3] au climat désabusé qui y dominait depuis un demi-siècle [4] pour les engager sur ce que Grothendieck nommera, un siècle et demi plus tard, « une longue marche », toujours en cours. [5]

Quel type de modernité mathématique émerge ainsi dans les « extensions et groupes de Galois » ? Comment, en algèbre, configurent-elles l’opposition du classique et du moderne ? [6] Ce renversement de l’algèbre (où désormais le polynôme structure le produit de ses zéros en groupe stable au lieu de le disperser en résolutions individuelles) peut-il intéresser aujourd’hui de tout autres types de modernités, ensablées dans leurs propres saturations, à commencer par la modernité musicale, engagée par Schoenberg, mise à mal après 1968 par la postmodernité et, depuis la mort de Carter et de Boulez, tenue pour forclose par la plasticité contemporaine de la performance, du mixage et de la numéricité ? [7] À quelles conditions serait-il possible de reprendre la longue marche de ces modernités (politiques, artistiques, amoureuses…) aux points mêmes où une mélancolie résignée [8] les a abandonnées ?

L’hypothèse sera qu’un certain style galoisien de pensée peut ici nous éclairer, nous guider et nous encourager. Nous en thématiserons, pour ce faire, les caractéristiques suivantes : réduplication (de l’énonciation), renversement (de la problématique), dualisation (des corrélations), extension (d’ensemble), adjonction (élémentaire) et renoncement (circonscrit), soit au total le faisceau de six gestes :

1. Rédupliquer (ou dialectiser) l’énoncé du problème dans son énonciation : Galois, en établissant la pensée algébrique dans ce qu’elle ne connait pas de l’inconnue sans plus la cantonner à ce qu’elle peut en connaître (c’est-à-dire à l’équation formalisant les relations connues de l’inconnue), dispose ainsi l’énonciation algébrique sous le signe même de l’inconnaissable qu’elle étudie. [9]

2. Renverser (ou retourner) l’ordre du problème en sorte de ressaisir le point où l’on bute comme la ressource d’où repartir : Galois « groupe » les racines algébriquement indiscernables pour mieux travailler la structure même de leur ambiguïté. [10]

3. Somme toute, dualiser (ou réciproquer) les deux faces du problème en les saisissant dans l’unité dialectique de leur opposition, dans l’ambiguïté duale de leur séparation [11] : Galois, prolongeant l’algébrisation cartésienne de la géométrie, géométrise l’algèbre des polynômes en sorte qu’on puisse interpréter et formaliser chacune en l’autre. Cette dualité (ou réciprocité) des rôles [12] est au cœur de la dimension fonctorielle de la « correspondance de Galois » : fonctorialité (contravariante) entre extensions de corps et réductions de groupes. [13]

4. Étendre, soit sortir de l’impasse par le haut en créant de nouvelles notions qui autorisent l’extension du domaine de travail : Galois, reliant la résolubilité de l’équation à son corps de résolution, explore les extensions de corps (donc de la situation constituante) qui vont autoriser de nouvelles possibilités.

5. Pour mettre en œuvre cette extension, adjoindre : Galois invente ce faisant la méthode si puissante de l’adjonction-extension. [14]

6. Last but not least, accepter de payer le prix du nouvel espace étendu en renonçant à ces premières motivations qu’il devient rétroactivement possible de caractériser comme une sorte de stade juvénile de la discipline : ainsi Galois défétichise [15] le millénaire désir algébrique de résolubilité. [16]

Au total, Galois contribue ainsi à l’histoire mathématique de ces révolutions où une notion de prime abord privative se retourne en socle affirmatif pour de nouveaux élans : l’inconnu (Al-Khawârizmî), l’irréductible (Galois), l’irrationnel (Dedekind), l’infini (Cantor), le non-euclidien (Riemann), l’invariant (Klein), l’incomplétude et l’indécidable (Gödel), l’irrégulier (Hironaka), l’indiscernable (Cohen), l’infinitésimal (Robinson, Conway), le non-commutatif (Connes), etc., toutes notions qui font bien sûr écho à l’inconscient (Freud). [17]

Tout ceci ne constitue-il pas une étonnante ressource mamuphique pour ceux qui, ne cédant pas sur leur désir de modernité musicale [18], devront, tôt ou tard, reconvertir la dimension soustractive et ascétique de sa séquence fondatrice (a-tonalité, a-thématisme et a-métricité) en la figure affirmative et expressive d’une troisième séquence [19], extrayant par le haut la composition moderne de son enlisement constructiviste (sérialisme) ?

Attendus

Il s’agit d’ouvrir ici un nouveau vaste chantier mamuphi sur la théorie de Galois, de sa naissance jusqu’à nos jours.

De l’algèbre en mamuphi …

Un précédent travail sur la théorie de Cohen (forcing) avait mis en évidence une généalogie ascendante Cohen→Galois, explicitée par Paul Cohen au début de son exposition du concept de forcing [20] : « La situation est analogue à la construction de l’extension d’un corps formée en adjoignant la racine d’une équation irréductible ƒ(x)=0. »

S’engager cependant dans un travail algébrique au long cours pose, à mon sens, un problème spécifique à mamuphi  : l’algèbre est en effet le lieu de ce que René Guitart appelle « la lettre aveugle », autant dire le lieu d’un calcul peu stimulant pour des intellectualités non mathématiques.

Ainsi dans la « pulsation géométrie-algèbre » (R. Guitart), l’intellectualité musicale s’inspire-t-elle plus volontiers de la géométrie – disons : de la figure géométrique et du diagramme.

La musique dispose en effet de sa propre algèbre (elle s’appelle solfège), de ses propres lettres (elles s’appellent notes), disons : de son propre ordre symbolique par formalisation littérale si bien que, sauf à déléguer ses calculs à l’algèbre (voie de l’informatique musicale), la musique a un imaginaire plus naturellement tourné vers le géométrique, le figural, le diagrammatique.

Il est vrai cependant que mamuphi est l’unité dialectique de deux voies :

1. la voie de l’application : celle où un problème musical trouve sa résolution par application mathématique ;

2. la voie des raisonances théoriques : celle des correspondances, des analogies, éventuellement des fonctorialités.

L’algèbre correspond plus naturellement à la voie-application car le calcul y est plus central - l’algèbre n’est-elle pas le site paradigmatique du calcul mathématique (même si, comme on va voir, Galois révolutionne cette caractérisation de l’algèbre) ?

Étudier la théorie de Galois fait exception à cette réserve mamuphique concernant l’algèbre car il s’agira pour nous, dans un premier temps, d’en étudier surtout la naissance (tout comme j’ai pu étudier la naissance de l’algèbre en général dans ce qui pouvait encore s’appeler légitimement « monde arabe » - Bagdad, 830 – ce qui m’a amené à soutenir que la langue arabe avait constitué le berceau de l’algèbre).

Étudier la naissance d’une théorie, c’est en effet non pas tant s’en saisir pour examiner ce qu’elle éclaire en aval d’elle-même qu’examiner ses conditions d’émergence, l’éclairer donc du point de son amont : comment a-t-elle pu se constituer, par quels gestes de pensée ?

Il va donc s’agir pour nous, au moins dans un premier temps, d’examiner la théorie moins dans son développement détaillé et la sinuosité de ses démonstrations que dans ses audaces constituantes, ses courages de pensée, ses élans pour dépasser les obstacles.

D’une singularité algébrique dans la théorie de Galois…

L’intérêt spécifique de cette théorie de Galois est en effet que les obstacles vont s’avérer être « franchis » sans qu’ils soient pour autant effacés ou dissous : ici les équations algébriques qui font obstacle à la résolution par radicaux vont bien rester définitivement irréductibles, irrésolubles donc ! Mieux, la théorie va démontrer que l’obstacle est bien infranchissable « par radicaux », que les racines de l’équation irréductible vont bien définitivement rester « hors-champ » de l’algèbre des nombres rationnels. Mais, en montrant que l’obstacle est ainsi bien réel, en démontrant le point de réel de l’impasse, la théorie va subsumer la situation donnant forme au problème. Elle ne va donc pas effacer l’impasse ; elle ne va pas détruire ou percer le mur qui la barre ; ce n’est pas non plus que la théorie va sortir de l’impasse en sautant, tel Icare, par-dessus le mur pour mieux ensuite le laisser derrière soi, l’abandonner à son sort d’obstacle localisé, le délaisser comme terrain inapproprié de jeu, comme dédale stérile pour la pensée. C’est plutôt qu’en comprenant le réel de cette impasse, l’impossible à franchir, la théorie va comprendre où situer cette impasse dans le champ global dont elle est l’impasse propre.

Ainsi l’impasse trouve sa solution en étant non pas minorée mais majorée comme point réel d’une situation globale : l’impasse ici, loin d’apparaître comme un égarement circonstanciel – une erreur d’aiguillage -, va valoir comme singularité au sens d’Hironaka c’est-à-dire comme faisant symptôme ponctuel d’une structure globale inapparente. L’impasse, ainsi comprise comme impasse réelle et nécessaire, et non plus comme défaut de connaissances ou de méthodes, avoue un secret de la situation globale.

C’est à ce titre que, en ces temps d’impasse pour bien des pensées, cette expérience-Galois peut s’avérer, pour nous non-mathématiciens, précieuse.

Elle incite d’abord à distinguer deux sortes d’impasses :

- des impasses conjoncturelle ou impasses par défaut (« faute de ceci ou de cela, on n’a pas encore trouvé le moyen de se faufiler ») ;

- des impasses structurelles ou impasses de structure, lesquelles ouvrent alors à deux voies possibles :

o celle de l’abandon et du déplacement procédant du diagnostic suivant : « la voie étant définitivement bouchée, il nous faut aller voir ailleurs » ;

o celle d’une mutation d’ensemble qui associe conversion des désirs, élargissement des problématiques et nouvelle vision d’ensemble – je propose de la nommer : passage d’un stade juvénile à un stade adulte de la problématique en question.

Galois est le nom d’un tel passage, d’une telle mutation dont tous les mathématiciens aujourd’hui conviennent de dire qu’elle est la mutation de la mathématique classique en la mathématique moderne.

D’une puissance de pensée spécifiquement moderne…

Prenons donc la théorie de Galois (1830) comme le geste fondateur de la modernité mathématique, un peu comme les Thèses sur Feuerbach (1845) et le Manifeste du parti communiste (1848) de Marx le sont pour la modernité politique ou les opus 10 (2° quatuor, 1908) à 21 (Pierrot lunaire, 1912) de Schoenberg le sont pour la modernité musicale.

Notre hypothèse de départ sera donc que cette mutation-Galois indexe une puissance spécifiquement moderne, qualitativement différente de la puissance classique, par exemple d’un Descartes (dont la mathématique - Géométrie - vient appuyer un Discours de la méthode où la raison classique s’attache à convertir le doute en certitude tout de même que l’algèbre classique convertit l’inconnu en connu pour peu, comme l’écrit Descartes dans ses Règles pour la direction de l’esprit, qu’elle ose « l’artifice de supposer connu ce qui est inconnu »).

Le trait frappant de cette mutation est qu’elle va libérer des forces stratégiques à très grande échelle temporelle (celle-là même que Grothendieck appelle « longue marche » et qui se prolonge depuis bientôt deux siècles).

Cette mutation ouvre donc une nouvelle ère – l’ère des mathématiques modernes.

J’aimerais au passage qu’on m’explique ce que de supposées « mathématiques romantiques » peuvent bien être. Qu’il y ait des mathématiciens romantiques, c’est une chose. Mais qu’il y ait des mathématiques intrinsèquement romantiques comme il y a bien des mathématiques intrinsèquement classiques et modernes, des musiques ou des poèmes intrinsèquement romantiques, toutes propositions attestables dans le détail intérieur des textes concernés, c’est une tout autre chose !

Le raz de marée déclenché par cette mutation – raz de marée très lent au demeurant à se déclencher mais ensuite d’autant plus irrésistible que ses élans contenus se seront longuement accumulés – peut, me semble-t-il, se périodiser entre trois étapes principales :

1) l’étape constituante : celle de Galois ;

2) l’étape de la généralisation et de l’élargissement : celle qu’on dira d’Artin - ici la théorie s’étend à la fois verticalement par abstraction et horizontalement par extension à d’autres équations que les équations polynomiales (équations trigonométriques, elliptiques, différentielles…) et à d’autres objets que les équations précédentes (généralisations du côté des corps ou des groupes, élargissements aux groupes de Galois arithmétiques ou géométriques, etc.) ;

3) l’étape de la mutation interne à la grande mutation-Galois : celle de Grothendieck (nouvelles généralisations et élargissements – K-algèbres, catégories de Galois, schémas… – autorisant une géométrisation systématique, via la théorie des catégories, de cette algèbre moderne).

D’une mutation réussie par la modernité mathématique dans les années 60

L’enjeu principal et ultime du chantier décennal que je propose d’ouvrir [21] serait de caractériser les gestes spécifiques de ce troisième temps dit Grothendieck, les ressources spécifiques de cette mutation interne à la modernité mathématique : là où les gestes constitutifs de la seconde étape sont clairement ceux de l’abstraction formalisante, de la généralisation et de l’élargissement, ceux de la troisième étape, sans renier les précédents, introduisent des gestes d’un autre type.

Indiquons d’ores et déjà un trait frappant [22] de ce troisième temps : Emil Artin (seconde étape) a formalisé une théorie de Galois généralisée (corps quelconque…) et ainsi aboutit à une exposition concentrée d’une extrême élégance et limpidité. Le problème est que, ce faisant, il a serti la théorie tel un diamant, fascinant mais corrélativement peu accessible aux appropriations particulières de la théorie.

Où l’on retrouve le danger de cette déviation qu’on dira formaliste [23] qui a contribué à l’impasse des secondes étapes pour les différentes modernités : sérialisme sans thématisme, structuralisme sans sujet, marxisme-léninisme sans liaison de masse, abstraction picturale sans figure [24], etc.

Les mathématiques s’en sont sorties dans les années 60 à la fois en se développant comme il est naturel en aval du point d’arrêt – en particulier par ces explorations des groupes de Galois qu’autorisaient les nouvelles puissances informatiques de calcul – mais également en amont, grâce cette fois à Grothendieck.

Arrêtons-nous un instant sur ce geste consistant à travailler en amont du point d’arrêt plutôt qu’à simplement et naturellement examiner son aval. Il est caractéristique de ce troisième temps qui est le nôtre car il est caractéristique d’un temps de reprise plutôt que de fondation.

Travailler l’amont immédiat d’un problème suppose de faire un léger pas en arrière pour examiner sous un autre jour le point d’arrêt, pour dégager un entour du point où les choses se sont cristallisées et figées.

Dans le geste en question de Grothendieck (celui, délimité, qui concerne la théorie de Galois), il ne s’agit pas à proprement parler d’examiner les « conditions de possibilité » de l’arrêt concerné, ni non plus son « transcendantal » (la structuration logique implicite de la situation générale). Mon hypothèse serait qu’il s’agit plutôt de remonter de l’énoncé à sa position d’énonciation : ici de remonter des énoncés algébriques Galois-Artin (sur les groupes) à leurs conditions géométriques d’énonciation. Le geste de Grothendieck reviendrait donc à poser qu’avant même le groupe, en amont de lui, il y a une géométrie à l’œuvre, un paysage à examiner, cet espace que j’appelle « hors-champ » du corps constituant, ce lieu spécifique que le groupe va venir structurer dans un temps second.

Cette hypothèse sera à travailler en détail ; elle intuitionne ce qui pourra, en cette affaire (malgré tout extrêmement technique et requérant un très lourd investissement pour s’approprier les mathématiques concernées), nous intéresser, nous non-mathématiciens désirer de penser aujourd’hui telle ou telle modernité spécifique à la lumière des mathématiques modernes et à l’ombre de la philosophie de notre temps.

De trois périodes dans les différentes modernités…

Soit une nouvelle hypothèse de travail : ces trois périodes de la modernité algébrique pourraient éclairer les problèmes aujourd’hui des autres modernités s’il est vrai que ce troisième moment de la modernité mathématique fait utile exception dans l’ensablement des différentes modernités autour de 68.

Il est en effet frappant qu’à bien y regarder, les mathématiques ont réussi, à partir des années 60, leur révolution dans la révolution moderne – on peut ici parler d’un « tournant géométrique dans la pensée » [25], déqualifiant l’ancien détestable « tournant linguistique » du Cercle de Vienne - là où les autres pensées non-scientifiques ont massivement échoué (à l’exception notable de la philosophie [26]) :

- voir, face à la peinture et à la sculpture modernes, l’hégémonie de « l’art contemporain » [27] ;

- voir le tournant de la musique moderne autour de 68 [28] ;

- voir l’ensablement progressif des politiques modernes d’émancipation, puis leur oubli (nostalgique) à partir de la fin des années 70 et finalement aujourd’hui leur forclusion (mélancolique) ;

- voir en amour, l’ensablement, après le moment lacanien, d’une pensée vive de la différence des deux sexes.

Sur ce fond, la mathématique fait donc exception victorieuse ! Tout projet de relancer les modernités selon une troisième vague stratégique ne peut donc qu’utilement tirer parti de son école.

Autant de raisons ainsi de nous pencher aujourd’hui sur la théorie de Galois pour en saisir ce que Gerard Manley Hopkins appellerait ses instress (ses intensions), autant dire son mouvement d’émergence, son énergie constituante, son audace subjective.

Tentons pour cela d’identifier les instress spécifiques de la théorie de Galois.

Entrons concrètement dans notre sujet par un exemple.

Un exemple

Une équation

Partons d’une équation, empruntée à Alain Connes [29] :

x⁵+x⁴-4x³-3x²+3x+1=0

Son graphe nous indique qu’elle a cinq racines réelles :

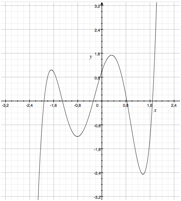
Nommons-les par valeurs croissantes : A, B, C, D, et E.

On peut approcher ces valeurs par calcul numérique :

A≃-1,918986… ; B≃-1,309721… ; C≃-0,28463… ; D≃0,83083… ; E≃ 1,682507…

Par une méthode qu’on ne précisera pas ici, on peut savoir que ce polynôme est irréductible et donc qu’aucune des racines A, B, C, D, E ne pourra être individuellement exprimée comme fonction algébrique des coefficients de l’équation.

On dira : l’ensemble (ou regroupement des cinq racines) ℰ={A, B, C, D, E} est défini par le polynôme [30] ℘= x⁵+x⁴-4x³-3x²+3x+1 mais il n’est pas pour autant déterminé si l’on entend ici par « déterminé » le fait d’être algébriquement déterminable (c’est-à-dire par radicaux) de l’intérieur même de la situation algébrique de départ (c’est-à-dire ici du corps des nombres rationnels ℚ, pris comme corps « de rationalité » du problème).

La situation algébrique constituante – le « corps de rationalité » - est ainsi faite d’objets (les éléments de ℚ c’est-à-dire les nombres dits rationnels) et d’opérations sur ces objets (celles de l’algèbre classique – addition/soustraction, multiplication/division, extraction de racines - résumées par l’expression « radicaux ») qui les maintiennent dans ℚ (qu’on appelle précisément « corps » en raison de cette clôture sur soi).

On dira que les racines A-B-C-D-E sont toutes hors-champ du corps constituant.

Mais leur ensemble (ou regroupement) ℰ, étant lui bien défini à partir de ℚ par ℘, n’est pas pour autant quelconque. Il constitue une sorte d’inconnu défini, tout comme, pour Al-Khawârizmî, x est un inconnu défini pour l’équation algébrique (polynomiale) de base P(x)=0.

Remarque

La langue française différencie ses articles en distinguant articles définis/indéfinis : par exemple, quand on dit en français « l’homme est naturellement bon », homme se dit avec l’article défini (on parle ici du type homme, défini par différence avec le type animal) lors même que l’homme en question restera indéterminé (générique). L’article, ici, définit le type sans déterminer l’individu.

Par contre, la langue arabe différencie ses articles en distinguant articles déterminés/indéterminés : si on parle en arabe de « l’homme », cela présupposera qu’il s’agit ici d’un homme déterminé (Alî ou Muhammad), ce qui dans l’exemple de notre phrase, n’a pas de sens. Pour dire la même chose, la langue arabe employera donc ici l’article indéterminé et énoncera : « dans un homme, il y a la bonté. »

Comme on va le voir, cette dialectique du défini et du déterminé est au cœur de notre problème algébrique.

Galois va travailler non plus comme Al-Khawârizmî sur les relations déterminables enserrant l’inconnue individuelle x (les relations de x à soi-même – notées xⁿ – et à des constantes qui sont algébriquement formalisées par l’équation) mais sur les propriétés définissables de l’inconnu collectif ℰ (relations de ℰ à lui-même qui vont être formalisées par le groupe algébrique).

On voit qu’il y a ici une extension du travail dans l’inconnu : on peut définir l’inconnu sans le déterminer. Ainsi, si l’équation algébrique classique travaille l’inconnue x pour la rendre ultimement connue (son but est la résolution de l’équation par détermination de son inconnue [31]), pour sa part le groupe de Galois va travailler ℰ pour mieux le définir comme indéterminable c’est-à-dire comme destiné à rester inconnu du point de vue de ℚ.

Cinq racines inconnues à cependant classer

Revenons à notre équation.

Remarquons ceci : même si aucun individu du collectif des racines n’est discernable algébriquement, le collectif comme tel est algébriquement discernable. En effet, on sait que l’on a :

x⁵+x⁴-4x³-3x²+3x+1=(x-A)(x-B)(x-C)(x-D)(x-E)

Et l’on sait, par développement du polynôme, que l’on a :

x⁵

-(A+B+C+D+E)x⁴

+(AB+AC+AD+AE+BC+BD+BE+CD+CE+DE)x³

-(ABC+ABD+ABE+ACD+ACE+ADE+BCD+BCE+BDE+CDE)x²

+(ABCD+ABCE+ABDE+ACDE+BCDE)x

-ABCDE=0

On en déduit donc que

· A+B+C+D+E=-1

· AB+AC+AD+AE+BC+BD+BE+CD+CE+DE =-4

· ABC+ABD+ABE+ACD+ACE+ADE+BCD+BCE+BDE+CDE =3

· ABCD+ABCE+ABDE+ACDE+BCDE =3

· ABCDE=-1

Autant donc de connaissances globales sur le collectif ℰ.

On se retrouve ainsi face au paradoxe suivant : le collectif des cinq racines est discernable algébriquement comme collectif alors qu’individuellement aucun de ses éléments (racines) ne l’est ; le collectif est défini mais aucun de ses éléments n’est individuellement déterminé.

En effet, au stade où nous en sommes, on connaît certaines relations internes à ℰ - on en connaît déjà cinq avec nos formules précédentes – mais on ne connaît bien sûr pas toutes ces relations (si on les connaissait toutes, on connaitrait alors la relation d’identité que chacune entretient avec elle-même et chaque racine serait ainsi déterminée) : par exemple, on ne connaît pas AC+BD+CE+DA+EB ou ABD+BCE+CDA+DEB+EAC. On connaît moins encore AB+CE, AB, A, etc.

L’idée est alors d’explorer les propriétés qu’on peut connaître de cet ensemble ℰ.

Ce faisant, on va opérer algébriquement sur l’ensemble inconnu ℰ un peu comme Al-Khawârizmî a opéré sur l’élément inconnu x : la méthode algébrique a en effet pour noyau fondateur l’idée de traiter l’inconnu comme s’il était connu en le nommant pour mieux le formaliser littéralement.

Face à un problème concret, Al-Khawârizmî traite l’inconnu comme s’il était connu en lui donnant un nom propre x en sorte d’examiner les relations connaissables de cet x (inconnu fictionné en connu) avec lui-même (x²) ou avec des quantités connues (constantes). D’où la formalisation de ce réseau de relations connues en un nouvel objet algébrique : l’équation.

En un sens, Galois fait de même en posant : « faisons comme si l’ensemble des racines inconnues était connu, donnons-lui le nom propre ℰ et examinons quelles relations cet ensemble entretient avec lui-même. » D’où la formalisation de ce réseau de relations connaissables en un nouvel objet algébrique : le groupe de Galois.

Attention : ce groupe de Galois n’est pas l’ensemble ℰ des racines (leur regroupement) mais un ensemble structuré (on va voir comment) d’opérations sur ℰ (celles qui vont le maintenir inchangé). [32]

Au total, comme Al-Khawârizmî est passé de l’inconnue à son équation (en fictionnant l’inconnue comme connue), Galois va passer de l’équation à son groupe ; le travail algébrique monte ainsi d’un cran : inconnu→équation→groupe.

Opérations sur un regroupement défini mais indéterminé

Quelles sont ces opérations ?

Ce sont – ce ne peuvent être – que des permutations P_i sur les éléments de cet ensemble ℰ, c’est-à-dire sur les racines de l’équation (ou zéros du polynôme).

Le point décisif va être de montrer que l’ensemble de ces permutations (leur regroupement 풢={P_i}) n’est pas seulement un tas, un paquet d’opérations mais a une structure interne particulière, celle précisément qui va prendre le nom de groupe : le regroupement 풢 (des permutations) vaut groupe au sens technique (algébrique) du terme alors que le regroupement ℰ des racines ne vaut pas groupe algébrique.

L’idée très simple est en effet la suivante : si l’on a deux permutations P_a et P_b des éléments de ℰ qui le maintiennent inchangé, alors les combinaisons successives P_a°P_b et P_b°P_a sont également des permutations maintenant ℰ inchangé et sont donc des éléments de 풢.

Vous voyez qu’on a maintenant à faire avec ce groupe 풢 à un ensemble d’un type très différent de notre ensemble ℰ de départ. ℰ={A,B,C,D,E}. En effet, la somme de deux éléments du groupe 풢 est toujours un élément du groupe 풢 alors que la somme de deux éléments de ℰ - mettons A+B - n’a par contre nulle raison d’appartenir à ℰ.

On peut ici savoir [33] que le groupe de Galois est stable par l’opération suivante [34] : x↦x²-2 ce qui revient à dire que si R est racine de P, alors (R²-2) le sera également :

Empiriquement, on peut tester ce point sur nos valeurs approchées :

A≃-1,92… ; B≃-1,31… ; C≃-0,28… ; D≃0,83… ; E≃1,68…

⟹ A²≃3,68… ; B²≃1,72…; C²≃0,08… ; D²≃0,79… ; E²=2,83…

⟹

C²-2 = A ≃ -1,92…

D²-2 = B ≃ -1,31…

B²-2 = C ≃ -0,28…

E²-2 = D ≃ 0,83…

A²-2 = E ≃ 1,68…

L’opération fait donc permuter nos cinq racines de la manière suivante :

· C↺A

· D↺B

· B↺C

· E↺D

· A↺E

Le groupe de Galois s’avère donc le groupe cyclique suivant :

A B C D E 

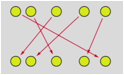
A B C D E 

Soit :

1	A	B	C	D	E
2	E	C	A	B	D
3	D	A	E	C	B
4	B	E	D	A	C
5	C	D	B	E	A
1	A	B	C	D	E

Il vaut donc mieux indexer nos cinq racines réelles A-B-C-D-E non plus par ordre croissant (de manière arithmétiquement « naturelle ») mais de cette manière A-B-E-C-D en sorte que la permutation {A,B,E,C,D} ↺ {E,C,D,A, B} devienne une simple translation. [35]

Notre groupe de Galois est ainsi mis au jour comme groupe (cyclique) des translations, qu’on peut figurer géométriquement comme groupe des rotations des sommets d’un pentagone :

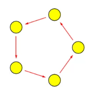
Correspondance de Galois

L’étape suivante est l’établissement d’une correspondance – dite correspondance de Galois – entre corps (de définition) et groupes (de symétries sur les racines).

Elle passe par un traitement en parties doubles :

- d’un côté extensions progressives du corps de départ par adjonctions de racines individuellement déterminées : ∆K

- de l’autre côté, réductions progressives du groupe de symétries sur un hors-champ progressivement réduit ∇G dont l’étape ultime est sa réduction à la seule permutation identité I.

L’enjeu sera alors d’établir les conditions d’une correspondance pas à pas entre ∇G et ∆K qui, conduisant jusqu’à G={I}, conduise dualement K jusqu’au corps étendu K[A,B,C,D,E] où toutes les racines deviennent algébriquement déterminables.

C’est là la correspondance galoisienne, qui peut être vue comme un foncteur contravariant (les mouvements corrélés se font en sens inverse : une réduction d’un côté est associée à une extension de l’autre) entre la catégorie des groupes et la catégorie des corps (les deux étant intérieurement structurées par la relation d’inclusion) : ∇G ⇄ ∆K

Le résultat, somme toute latéral de cette vaste compréhension du problème initial, sera une caractérisation précise du groupe de Galois (d’une équation algébrique donnée) autorisant ou interdisant qu’elle soit résoluble par radicaux.

Alliage de six gestes galoisiens de pensée

Revenons maintenant à notre enjeu fondamental : caractériser les gestes galoisiens de pensée, au principe de cette révolution algébrique.

Nous en proposerons six, étroitement coordonnés : la réduplication (de l’énonciation), le renversement (de la problématique), la dualisation (des corrélations), l’extension (d’ensemble), l’adjonction (élémentaire) et le renoncement (circonscrit).

1. Rédupliquer

Rédupliquer (ou redoubler [36] ou dialectiser) l’énoncé du problème dans son énonciation : Galois, en établissant la pensée algébrique dans ce qu’elle ne connait pas de l’inconnue sans plus la cantonner à ce qu’elle peut en connaître (c’est-à-dire à l’équation formalisant les relations connues de l’inconnue), dispose ainsi l’énonciation algébrique sous le signe même de l’inconnaissable qu’elle étudie. On dira qu’avec Galois l’énoncé algébrique devient saisi selon une énonciation elle-même algébrique.

Le mathématicien Gustave Verriest formule ainsi [37] les bonds successifs :

« En arithmétique, on fait des opérations déterminées sur des nombres déterminées, en algèbre [classique] on fait des opérations déterminées sur des nombres non déterminés, dans la théorie des groupes abstraits [algèbre moderne], on étudie des opérations non déterminées effectuées sur des objets non déterminés. » [38]

Travailler ce que l’on ne sait pas de l’inconnu – ce qui va se dire : travailler les symétries du regroupement inconnu ℰ={A,B,C,D,E} – va conduire au fait que l’inconnu n’est plus normé par le connu, l’inconnu n’est plus saisi comme ce qui devant être connu ne l’est pas encore, comme ce qui est destiné à devenir, tôt ou tard, connu.

Le parallèle ici avec l’inconscient freudien s’impose : l’inconscient n’est pas un conscient potentiel non encore advenu, un défaut de conscience réparable mais la structure même qui autorise le langage et la conscience. C’est alors la conscience qui devient sous la norme de l’inconscient (et non pas l’inverse) : la conscience devient ce qui n’est pas inconscient comme, à partir de Dedekind, le fini devient ce qui n’est pas infini.

Ici ce qu’il y a d’inconnu en ℰ devient l’effet de ses propriétés de symétrie, et le connu devient alors ce qui n’a plus de symétries internes. L’inconnu peut désormais être saisi en soi et non plus dans une détermination à s’éponger en connu.

2. Renverser

Renverser (ou retourner) l’ordre du problème en sorte de ressaisir le point où l’on bute comme la ressource d’où repartir : Galois « regroupe » les racines algébriquement indiscernables pour mieux travailler la structure même de leur ambiguïté (Galois nomme ambiguïté la symétrie du regroupement des racines).

Ici le problème n’est plus le lieu à faire disparaître (une fois la solution trouvée) mais le lieu de type nouveau d’où repartir, une fois bien comprise sa structure propre d’ambiguïté.

Verriest à nouveau expose cela dans une grande clarté :

« Le trait de génie de Galois, c’est d’avoir découvert que le nœud du problème réside non pas dans la recherche directe des grandeurs à adjoindre, mais dans l’étude de la nature du groupe de l’équation. Ce groupe exprime le degré d’indiscernabilité des racines ; il caractérise donc non pas ce que nous savons des racines mais, au contraire, ce que nous n’en savons pas. Or, lorsque je veut résoudre une équation, ce qui mesure la difficulté de cette recherche, ce n’est pas ce que je sais déjà des racines mais, au contraire, ce que j’en ignore. […] Ce n’est donc plus le degré d’une équation qui mesure la difficulté de la résoudre mais c’est la nature de son groupe. » [39]

3. Dualiser

Somme toute, dualiser (ou réciproquer) les deux faces du problème en les saisissant dans l’unité dialectique de leur opposition, dans l’ambiguïté duale de leur séparation : Galois, prolongeant l’algébrisation cartésienne de la géométrie, géométrise l’algèbre des polynômes en sorte qu’on puisse interpréter et formaliser chacune en l’autre.

Cette dualité (ou réciprocité) des rôles est au cœur de la dimension fonctorielle de la « correspondance de Galois » : fonctorialité (contravariante) entre extensions de corps et réductions de groupes – la réduction du groupe G est associée à une extension du corps K :

∇G ⇄ ∆K

On peut dire qu’il s’agit ce faisant d’apprendre à travailler « en parties doubles », ou à marcher sur deux jambes, ou encore à constituer une médaille à deux faces en sorte que la pulsation de l’une à l’autre fasse avancer les choses.

4. Étendre

Étendre, soit sortir de l’impasse par le haut en créant de nouvelles notions qui autorisent l’extension du domaine de travail : Galois, reliant la résolubilité de l’équation à son corps de résolution, explore les extensions de corps (donc de la situation constituante) qui vont autoriser de nouvelles possibilités.

5. Adjoindre

Pour mettre en œuvre cette extension, adjoindre : Galois invente ce faisant la méthode si puissante de l’adjonction-extension.

Rappelons qu’adjoindre est bien plus qu’ajouter : on ajoute un élément (par ex. √2 à ℚ) mais on l’adjoint si, de plus, on le combine avec tous les anciens éléments (p, q…) pour ainsi composer un corps étendu :

ℚ[√2]={p+q√2}

C’est de cette manière que l’extension peut constituer un bouleversement radical et global (non pas un rafistolage latéral ou une réforme circonstanciée) du domaine de départ, autant dire une révolution.

6. Renoncer

Last but not least, accepter de payer le prix du nouvel espace étendu en renonçant [40] à ces premières motivations qu’il devient rétroactivement possible de caractériser comme une sorte de stade juvénile de la discipline : ainsi Galois défétichise le millénaire désir algébrique de résolubilité.

Ce geste d’acceptation circonscrit le point de « castration » qui accompagne nécessairement le passage qu’on a appelé du stade juvénile au stade adulte : il faut renoncer sur un front secondaire pour pouvoir gagner sur le front principal.

Si, comme on l’a signalé plus haut en note, le renoncement à la résolubilité par radicaux n’est pas anodin pour le désir algébrique, ne voit-on pas tout de même combien le nécessaire renoncement des politiques modernes d’émancipation à toute intériorité étatique (spécifiquement en leur troisième étape) est lui-même difficile.

Un alliage

Au total, le style galoisien de pensée coordonnerait étroitement le fait de :

– rédupliquer l’inconnu en travaillant une énonciation intrinsèquement ambigüe sur l’inconnu ;

– renverser le problème en travaillant directement un hors-champ défini non plus comme envers (ou complémentaire) illimité du champ mais comme son hors-champ, délimité dans une extériorité sans limites (ici celle des nombres) ;

– dualiser le problème selon deux faces en correspondance fonctorielle en sorte que le problème devienne explorable au gré d’une marche sur deux jambes, dont l’intérêt principal sera de comprendre l’être structural du hors-champ - qu’il s’avère finalement réintégrable dans le champ des radicaux relève alors ici d’un intérêt secondaire ;

– étendre le champ constituant du problème posé par adjonctions élémentaires successives pour mieux éclairer la dialectique unificatrice du champ et de son hors-champ ;

– renoncer à une conception réductrice (« juvénile ») de ce que veut dire ‘résoudre le problème’ pour avancer une conception plus ample (« adulte ») ce que veut dire le solutionner, sous le signe désormais de sa compréhension structurale plutôt que de sa résolution utilitaire par radicaux [41] : la solution du problème n’est plus nécessairement sa résolution (et donc sa dissolution comme problème) ; un problème irrésoluble peut être solutionné.

Annexes

D’une mélancolie mathématicienne précédant l’événement-Galois

Lagrange

Lettre à d’Alembert du 21 septembre 1781 :

« Je commence à sentir que ma force d’inertie augmente peu à peu, et je ne réponds pas que je fasse encore de la Géométrie dans dix ans d’ici. Il me semble aussi que la mine est presque déjà trop profonde, et qu’à moins qu’on ne découvre de nouveaux filons, il faudra tôt ou tard l’abandonner. La physique et la chimie offrent maintenant des richesses plus brillantes et d’une exploitation plus facile ; aussi le goût du siècle paraît-il entièrement tourné de ce côté-là, et il n’est pas impossible que les places de la Géométrie dans les Académies ne deviennent un jour ce que sont actuellement les chaires d’arabe dans les Universités. »

Cauchy

Discours Sur les limites des connaissances humaines le 14 novembre 1811 à Cherbourg :

« On est tenté de croire que les connaissances de l’homme peuvent croître et se multiplier à l’infini. »

« Cependant si l’on observe que toute notre intelligence et nos moyens sont renfermés entre des limites qu’ils ne peuvent jamais franchir, on se persuadera sans peine que nos connaissances sont bornées comme nos facultés. »

« Que dirais-je des sciences exactes : la plupart paraissent parvenues à leur plus haute période. L’arithmétique, la géométrie, l’algèbre, les mathématiques transcendantes sont des sciences que l’on peut regarder comme terminées, et dont il ne reste plus à faire que d’utiles applications. »

D’un nécessaire renoncement…

Gustave Verriest

« Si un lecteur non initié était porté à croire que la théorie de Galois lui apportera de nouvelles formules pour la résolution des équations, il irait au-devant d’une déception. » « Le but de la théorie de Galois n’est pas de fournir des formules pour la résolution des équations. » [42]

« N’oublions pas que le but principal de l’algèbre n’est nullement de fournir aux calculateurs des méthodes pratiques de calcul. Nul ne contestera qu’en trouvant la formule de résolution de l’équation général du quatrième degré, Ferrari a fait une découverte extrêmement intéressante et cependant jamais cette formule n’a servi à calculer pratiquement les racines d’une équation donnée du quatrième degré ; cette formule conduit, en effet, à des calculs sensiblement plus longs que ceux qu’exigent les méthodes d’approximation. Pour le praticien, il n’est d’aucun intérêt de savoir si l’équation qu’il doit résoudre est ou n’est pas résoluble par radicaux. La seule chose qui l’intéresse est d’avoir une méthode qui lui permette de calculer rapidement les racines avec le nombre voulu de décimales exactes. » [43]

Olivier Debarre

« Les mathématiciens du temps de Galois ont considéré que ces critères de résolubilité des équations de degré premier ne donnaient pas une réponse qu'ils estimaient satisfaisante à la question car ces critères nécessitaient de connaître des informations à priori sur les racines. En fait, ils attendaient plutôt un critère général ne faisant intervenir que les coefficients de l'équation et permettant de savoir, par simple inspection de ce coefficient, si l'équation était ou non résoluble par radicaux.

La théorie de Galois, très en avance sur son temps, et montrant que le problème était bien plus subtil, ne correspondait pas à ces attentes. Et ce n'est que beaucoup plus tard que le monde mathématique a commencé à réaliser que la théorie de Galois allait bien au-delà du problème, somme toute très artificiel, de la résolution par radicaux des équations algébriques. Galois avait en fait propulsé tout le domaine de l'algèbre dans un nouveau monde : celui des groupes, des extensions de corps, et de bien d'autres concepts fondamentaux des mathématiques d'aujourd'hui.

En particulier, de nos jours on s'est rendu compte qu'il est bien plus important de savoir calculer le groupe de Galois d'un polynôme, plutôt que de savoir s'il est résoluble par radicaux. » [44]

Douze moments mathématiques où ce qui fut soustrait se convertit en affirmation

Mathématiques grecques

1. l’irrationnel avec les Grecs → le nombre algébrique puis réel

Mathématiques classiques

2. l’inconnu avec Al-Khawârizmî (830) → le résoluble (par radicaux)

Mathématiques modernes

(Période I)

3. l’irrésoluble avec Galois (1830) → l’ambigu comme symétrique

4. le non-algébrique avec Liouville (1844) → le transcendant

5. le non-euclidien avec Riemann (1854)

6. l’infini avec Dedekind (1860) → le fini comme non-infini

7. l’invariant avec Klein (1873) → le géométrique

(Période II)

8. l’incomplétude et l’indécidable avec Gödel (1935)

(Période III)

9. l’irrégulier avec Hironaka (1964) → la singularité

10. l’indiscernable avec Cohen (1964) → le générique

11. le non-standard / l’infinitésimal avec Robinson et Conway (années ’60) → le nombre surréel

12. le non-commutatif avec Connes (années ’80)

***

---

[1] Bibliographie :

• Ian Stewart : Galois Theory (Third Edition)

• Antoine Chambert-Loir : Algèbre corporelle

• Olivier Debarre et Yves Laszlo : Introduction à la théorie de Galois (www.coursera.org/learn/theorie-de-galois).

La dernière référence (cours en ligne de l’Ens) adopte un mode d’exposition bourbakiste, celui-là même dont Stewart, pour sa part, choisit explicitement, dans sa troisième édition, de prendre l’exact contre-pied en partant non plus du cas général pour ensuite le particulariser (d’abord n dimensions, puis « soit n=2 ») mais, à l’inverse, en partant du cas le plus simple pour ensuite le généraliser (d’abord 2 dimensions, puis « soit 2=n »), en partant donc ici de ℚ et ℂ pour ensuite généraliser à K et Ω. Le second ouvrage occupe une position intermédiaire entre ces deux modes contrastés d’exposition.

[2] Tout de même que l’équation algébrique P(x)=0 s’avère n’être pas toujours résoluble algébriquement (c’est-à-dire par radicaux), l’équation arithmétique a2+b2=n2 s’était avérée pour les Grecs n’être pas toujours résoluble arithmétiquement (c’est-à-dire sur les rationnels, les seuls nombres alors existants) : ainsi, si 3²+4² l’est bien (car n=√25=5 est rationnel), par contre 1²+1² ne l’est plus (car n=√2 est irrationnel).

[3] Au moins à deux reprises (830, Al-Khawârizmî ; 1830, Galois), l’algèbre a ainsi joué un rôle proprement stratégique dans le développement et l’unification des mathématiques toutes entières : en 830, comme création d’un troisième continent, médiateur entre les continents arithmétique et géométrie, disjoints depuis la crise des irrationnels (toute grandeur géométrique n’équivaut pas à une quantité numérique) et dogmatiquement séparés par Aristote (les démonstrations ne doivent pas circuler entre les deux) ; en 1830, comme relance, par inversion, du croisement algèbre-géométrie, au fondement, deux siècles plus tôt, du cartésianisme : là où Descartes interprétait algébriquement la géométrie, Galois interprète géométriquement l’algèbre (le « groupe de Galois » a pour paradigme naturel des symétries spatiales).

[4] Laplace, 21 septembre 1781 : « La mine [de la géométrie] est presque déjà trop profonde, et, à moins qu’on ne découvre de nouveaux filons, il faudra tôt ou tard l’abandonner. »

Cauchy, 14 novembre 1811 : « L’arithmétique, la géométrie, l’algèbre, les mathématiques transcendantes sont des sciences que l’on peut regarder comme terminées, et dont il ne reste plus à faire que d’utiles applications. »

Pour citations complètes, voir « Annexes »

[5] On peut ainsi dire de l’événement « Algèbre de Galois » ce que Marx dira de l’événement « Commune de Paris » : « la plus grande mesure qu’elle ait prise, c’est sa propre existence ».

[6] Rappelons qu’Albert Lautman thématisait cette opposition du classique et du moderne en mathématique comme étant l’opposition de l’analyse et de l’algèbre.

[7] Le séminaire mamuphi consacrera une journée (samedi 10 mars 2018) à l’examen de cette opposition modernités/contemporanéisme.

[8] C’est Michel Foucault qui, à la fin des années 70, en a donné le « la » dépité en déclarant que, désormais, la révolution politique n’était plus désirable…

[9] Ce geste galoisien suggère qu’aujourd’hui, prolonger les différentes modernités impliquerait de les rédupliquer, c’est-à-dire de constituer une nouvelle conception proprement moderne des modernités et non plus seulement une conception moderniste (qui majore unilatéralement la rupture du moderne avec le classique) ou classiciste (qui, à l’inverse, majore unilatéralement sa continuité avec le classique), contemporanéiste (celle des visions nihilistes du moderne qui actuellement déferlent) ou romantique (voir, par exemple, ce « romantisme révolutionnaire » prôné dès les années 60 par Henri Lefebvre), voire baroque (tentant, selon une inspiration ultimement religieuse, d’incorporer la modernité à la tradition de l’Un et du Tout cosmique). Tout de même qu’Adorno posait qu’une philosophie de la musique moderne se devait d’être une philosophie moderne de la musique (et non pas une philosophie traditionnelle), tout de même que la mathématique pose qu’une reprise de l’algèbre moderne (galoisienne) se doit d’être une reprise moderne de l’algèbre (s’entend : axiomatisée et géométrisée), tout de même un programme de reprise de toute pensée moderne se devrait d’être un programme moderne, sachant que ce que veut exactement dire « programme moderne » pourrait ici s’éclairer d’un examen comparé des différents programmes mathématiques depuis Galois : ceux de Klein (Erlangen, 1872), de Hilbert (1900), de Langlands (1967), de Grothendieck (Esquisse d’un programme, 1984)…

[10] En un certains sens, ce geste étend le geste même de l’algèbre s’il est vrai, comme l’écrivait Descartes dans sa Géométrie, que « faire venir une équation pour résoudre un problème », c’est « le considérer comme déjà fait ».

[11] Galois, traitant l’ambiguïté non plus comme négativité en impasse mais comme structure positive de départ, inverse le sens des inférences et ce faisant les dualise (au sens catégoriel du terme où l’on passe d’une catégorie à sa duale par inversion des morphismes).

Quelques décennies plus tard, Dedekind inversera (dualisera) de même ses enchaînements pour fonder les nombres réels par coupures des rationnels : {nombre rationnel ⟹ coupure} ↺ {coupure ⟹ nombre réel}.

[12] Cette réversibilité fait écho avec ce que Lautman appelle « rapports d’expression ou d’imitation ».

[13] Le couplage au principe de cette fonctorialité permet de remplacer l’étude directe de l’extension par l’analyse de son groupe de Galois.

[14] 130 ans plus tard, Paul Cohen s’inspirera explicitement de ce geste galoisien pour étendre, par forcing, une situation de départ en lui adjoignant un élément générique. Ce faisant, Cohen construira un système de nomination par polynômes qu’on peut concevoir comme des sortes de polynoms (voir l’exposé mamuphi du 27 mai 2017)

[15] Olivier Debarre (2015) : « Les mathématiciens du temps de Galois ont considéré que ces critères de résolubilité des équations de degré premier ne donnaient pas une réponse qu'ils estimaient satisfaisante à la question. […] La théorie de Galois, très en avance sur son temps, […] ne correspondait pas à ces attentes. Et ce n'est que beaucoup plus tard que le monde mathématique a commencé à réaliser que la théorie de Galois allait bien au-delà du problème, somme toute très artificiel, de la résolution par radicaux des équations algébriques. Galois avait en fait propulsé tout le domaine de l'algèbre dans un nouveau monde […]. De nos jours on s'est rendu compte qu'il est bien plus important de savoir calculer le groupe de Galois d'un polynôme plutôt que de savoir s'il est résoluble par radicaux. »

Pour citation complète, voir « Annexes »

[16] Pour mesurer l’ampleur du renoncement galoisien, rappelons que l’algèbre a tiré son nom propre du mot arabe « réduction » (al-jabr) pour constituer ainsi ses équations dans l’horizon de cette réductibilité… à laquelle Galois l’incitera, un millénaire plus tard, à renoncer. Qu’un tel renoncement, nécessaire à la refondation de l’algèbre, ait dû prendre des décennies n’est que trop naturel, tout comme de nos jours le nécessaire renoncement de la politique émancipatrice de l’égalité à son ancienne prétention scientifique (matérialisme historique) ne saurait s’opérer en un éclair – il est vrai que lui manque encore la face affirmative, extensive et enthousiasmante, d’une recomposition galoisienne.

[17] Dans chacun de ces cas (revoir en « Annexes » une liste de douze moments), le négatif concerné devient symptôme d’une possibilité de type nouveau qui ne peut voir le jour dans le cadre du dispositif existant si bien que le travail de conversion du négatif s’apparente ici à l’aveu d’un secret longuement gardé : la symétrie de groupe que l’irréductibilité de l’équation recouvre (Galois), la singularité à portée globale que l’irrégularité apparente dissimule (Hironaka), etc.

[18] ceux-là donc qui n’envisagent nullement de devenir Amfortas, capitulant face au Klingsor contemporain et, qui s’attachent, tel Gurnemanz avant que l’événement-Parsifal ne vienne ressusciter la subjectivation-Kundry, à transmettre la flamme par quelque œuvre d’entretemps…

[19] Ce nouveau moment moderne devra trouver comment s’inspirer du « tournant géométrique » engagé par les mathématiques dans les années 60 : il est en effet frappant qu’au moment même où bien des modernités s’enlisent, celle des mathématiques, par contre, engage sa propre mutation à grande échelle. Ainsi, si la constitution des modernités face aux classicismes peuvent s’éclairer de la mathématique de Galois, la continuation de ces modernités face au contemporain devra sans doute s’éclairer de la mathématique de Grothendieck et de Langlands (le « programme de ce dernier, symptomalement daté de 1967, ne suggèrerait-il pas que le temps des programmes pourrait être revenu pour les différentes pensée modernes : non plus certes, comme dans les années 20, les programmes esthétiques des avant-gardes mais plutôt des programmes stratégiques de travail ?)

[20] Set Theory and the Continuum Hypothesis (Benjamin/Cummings, p. 113)

[21] Il concernerait la troisième décennie mamuphi (tout a commencé, je le rappelle, fin 1999)

[22] Je dois à Pierre Cartier d’avoir attiré mon attention sur ce point lors de la discussion mamuphi de cet exposé.

[23] Appelons ici « déviation formaliste » ou « formalisme » une conception réductrice de la formalisation qui prétend la dispenser de toute interprétation, qui s’autorise des pouvoirs de sa nécessaire cohérence pour prôner univoquement une syntaxe économisant toute sémantique…

[24] Le figural de Klee n’est pas plus un figuratif (et c’est bien pour cela que Boulez s’y intéressait de près dans les années 80 où il tentait d’inventer un thématisme de type nouveau, apte à sortir le sérialisme de son impasse formaliste qui niait les lois de la perception comme le formalisme nie celles de l’interprétation sémantique) qu’à l’envers, la formalisation n’est nécessairement un formalisme…

[25] Ce tournant concerne mathématique (Grothendieck), logique (Girard) et philosophie (Badiou).

[26] Voir ici, exemplairement, la philosophie d’Alain Badiou – n’est-ce pas d’ailleurs pour cette raison précise que tous ceux qui font commerce de la pente nihiliste contemporaine se coalisent aujourd’hui pour l’ostraciser de l’Université ?

[27] Deux emblèmes du nouvel « art contemporin » ont été d’un côté la Biennale de Venise accordant fin 1964 son Grand Prix de la peinture au pop-art de Rauschenberg, et d’un autre côté la création en France d’Art Press fin 1972.

[28] qui concerne simultanément rien de moins que Boulez, Stockhausen, Berio, Zimmermann, Pierre Henry, le free-jazz…

[29] https://www.youtube.com/watch?v=qrpp1Mh8EDo

[30] Il faut ici entendre un polynôme comme une sorte de nom algébrique (de polynom) donné à l’ensemble des racines qu’il définit.

[31] C’est ce qu’Al-Khawârizmî appelle « réduction » et « comparaison ». Ce qui, chez Galois, va remplacer la réduction (passage de part et d’autre du signe « = ») et la comparaison (simplification des monômes de même ordre) d’Al-Khawârizmî va être les ℚ-automorphismes du corps étendu ℚ[A,B,C,D,E] c’est-à-dire les symétries selon le hors-champ qui restent indiscernables de l’intérieur de ℚ.

[32] En ce point, le mémoire originaire de Galois ne distingue pas encore clairement groupement des racines en un ensemble ℰ et groupe des opérations sur cet ensemble ℰ (celui qu’on dira ultérieurement des automorphismes)…

[33] On verra comment lors de l’atelier.

[34] On parle ici de « générateur » du groupe…

[35] C’est sans doute là ce que Galois appelait « classer les opérations suivant leur difficulté et non suivant leur forme »…

[36] Au sens ici précis d’un redoublement de l’énoncé sur l’énonciation…

[37] Leçons sur la théorie des équations selon Galois (1939, rééd. Gabay 1997)

[38] Appendice. La théorie de Galois

[39] Appendice. La théorie de Galois

[40] « Aucune valeur n’est spécifiquement humaine si elle n’est pas le résultat d’un renoncement et d’une conversion. » Bachelard (Lautréamont)

[41] Les mathématiciens Verriest et Demarre (voir annexe) font d’ailleurs remarquer qu’il y a quelque fétichisme à focaliser le désir mathématique sur les formules d’une résolution par radicaux : la résolution numérique (par valeurs approchées des racines) est en général beaucoup plus rapide et d’une plus grande utilité pour le calcul. Si le groupe de Galois est donc solution du problème posé par l’équation algébrique, c’est au titre du travail algébrique qu’il autorise, travail dual, à deux faces, puisque la manière même dont ce travail démontre l’irrésolubilité algébrique crée les nouvelles notions qui vont constituer la solution effective du problème.

[42] Préface

[43] Appendice. La théorie de Galois

[44] https://www.coursera.org/learn/theorie-de-galois/lecture/efQvs/video-3-le-cas-des-equations-de-degre-premier