 Musique,
mathématiques et philosophie
Musique,
mathématiques et philosophie Musique,
mathématiques et philosophie
Musique,
mathématiques et philosophie
François Nicolas
Je voudrais formuler la question suivante : quelles sont
les limites musicales de la formalisation mathématique
?
Les apports de cette formalisation sont indéniables et
je demande donc de ne pas interpréter ma question comme
une méfiance à l'égard des mathématiques.
Il s'agit seulement à mes yeux d'établir une évaluation
matérialiste de cette formali-sation, ou encore d'identifier
son point de réel sous l'hypothèse lacanienne rabâchée
que le réel, c'est l'impossible (l'impossible pointe le
réel bien mieux que ne le fait le possible).
Il me semble alors qu'un débat latent court dans notre
sé-minaire qui peut se décrire ainsi :
- il y a ceux qui pensent que mathématiques et musique
cons-tituent un espace de pensée relativement homogène,
dans lequel les diagrammes, tel celui présenté par
Moreno Andratta, peuvent être commutatifs (et il m'a semblé
que le « principe anthropique » avancé par
Guerino Mazzola exposait en fait cette conviction fondamentale)
;
- et il y a ceux, comme moi, qui soutiennent que mathémati-ques
et musique constituent deux espaces de pensée radicale-ment
hétérogènes et disjoints si bien que les
diagrammes cir-culant entre musique et mathématiques ne
sauraient être com-mutatifs.
Essayons de préciser et d'argumenter cela.
Le possible de la formalisation mathématique - «
ce qui marche » - tient à la dimension d'ontologie
des mathémati-ques : pensant l'être, ce qu'elle pense
vaut ipso facto de tout ce qui est, en particulier dans
le domaine sonore : si 7+5 = 12 (exemple élémentaire
pris par Kant !), ceci vaut pour les pom-mes de terre comme pour
les accords de musique ou pour les planètes. Il y a donc
un efficace des mathématiques, en musi-que comme ailleurs,
qui à mon sens ne soulève aucune interro-gation
particulière (si l'on accepte bien sûr la thèse
que les mathématiques sont l'ontologie). Mais à
dire vrai, dans ce cas les mathématiques ne sont pas exactement
une formalisation. Elles sont plutôt le cadre de pensée
ontologique dans lequel sont ressaisies les propriétés
de tel ou tel type d'étants particu-liers. Pour penser
une dimension supplémentaire de la théorie mathématique
sur la musique qu'on nommera alors spécifi-quement formalisation,
il faut, me semble-t-il, ajouter autre chose, et spécifiquement
en passer par la théorie logique des modèles.
Dans cette théorie, un système formel est un ensemble
de signes (de lettres et de symboles), doté d'une grammaire
(pour déterminer les expressions « bien formées
»), de règles de déduction (le modus ponens,
etc.), bref un système syntaxique qui va être accompagné
d'une sémantique c'est-à-dire d'une interprétation
de ces signes dans un domaine de référence constituant
le modèle pour cette formalisation.
Un point essentiel, au coeur de cette « théorie des
modè-les », est que s'il y a une interprétation
des lettres d'individus, il n'y en a pas des signes logiques tel
celui de l'implication. On a donc un schéma qui opère
ainsi :

Le point capital est que si de a vers A, ou de b vers B, il
y a bien formalisation (et à l'inverse, de A vers
a et de B vers b, il y a bien interprétation), par
contre il n'y a pas d'interprétation de la flèche
qui dans le système formel va de A vers B : on peut évaluer
A comme on peut évaluer B, mais on ne saurait évaluer
(dans le modèle) la flèche. Comment fait-on alors
pour évaluer la proposition (A => B) ? On passe par
une table de vérité, examinant si a (qui correspond
à A) est vrai ou faux, et de même pour b, et on déclare
que (A => B) sera interprétable comme vrai dans
le modèle si l'on n'a pas à la fois v(a) et f(b),
c'est-à-dire si on n'a pas à la fois « a vaut
vrai » et « b vaut faux ». Dans tous les autres
cas, ce « sera » vrai (cf. la « table de vérité
» ci-dessous).
|
|
|
|
|
|
|
|
|
|
|
|
Le point essentiel est donc que l'enchaînement qui existe
dans la théorie (ou système formel) n'a aucune équivalence
dans le modèle. Par exemple (A => B) sera considéré
comme valide si f(a), c'est-à-dire si « a vaut faux
» (ex falso sequitur quodlibet : du faux peut suivre
ce qu'on veut...). Donc dans le modèle a et b peuvent ne
pas être du tout corrélés entre eux alors
que A et B le sont dans la théorie.
Le diagramme précédent n'est donc aucunement un
dia-gramme commutatif : il n'existe pas de flèche dans
le modèle allant de a vers b qui le ferait commuter.
Rappelons que le diagramme commuterait s'il existait une flèche
allant directement de a vers b telle que ce soit « pareil
» d'aller de a vers b directement par cette flèche
ou indirectement en passant par A puis B.
En fait il y a ici une barre horizontale qui sépare le
modèle de sa théorie (c'est-à-dire de sa
formalisation), barre qui inscrit l'existence de deux ordres de
pensée ne se recouvrant pas. D'où tous les théorèmes
logiques articulant le vrai (ce qui relève du modèle)
et le calculable ou démontrable (ce qui relève de
la théorie ou de la formalisation), et l'on sait que l'on
ne saurait avoir vrai Ûcalculable (il y a du vrai incalculable,
et il y a du calculé qui est « bizarrement »
vrai car vrai pour un tout autre modèle dit « pathologique
»...).
Dans notre cas, le modèle, c'est la musique et la formalisa-tion,
c'est la théorie de la musique.
On peut alors espérer s'en sortir en inscrivant une couche
supplémentaire, intermédiaire entre la théorie
mathématique de la musique et la musique elle-même,
couche constituée de la théorie musicienne de la
musique. On aura alors un nouveau schéma ainsi présentable
:
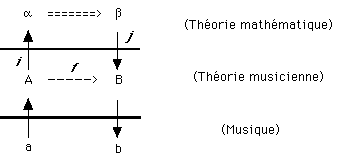
On dira alors que, si le diagramme a-A-B-b n'est pas com-mutatif,
par contre celui A-a-b-B pourra l'être. On ajoutera également
que ce nouveau diagramme étagé dissout les barres
horizontales entre domaines puisque
- la frontière entre « musique » et «
théorie musicienne de la musique » ne saurait être
un abîme,
- et que la frontière entre « théorie mathématique
» et « théorie musicienne », étant
frontière entre deux champs théori-ques, ne saurait
non plus être un gouffre.
On aurait ainsi créé des médiations aptes
à transiter sans dis-continuité majeure entre musique
et mathématiques !
Je soutiendrai pour ma part que ce diagramme étagé
n'est pas plus commutatif que le précédent et qu'il
ne résorbe aucu-nement les abysses existant entre ces trois
ordres :
- ni le premier étage (a-A-B-b) n'est commutatif (pour
les mêmes raisons que précédemment : sans
doute une théorie musicienne n'est pas exactement une formalisation
mathémati-que mais cependant le principe s'y maintient
qu'on ne saurait traduire dans le sensible de la musique ce que
la théorie musi-cienne a corrélé),
- ni le second (A-a-b-B) car la théorie musicienne ne saurait
être isomorphe à une théorie mathématique
: ce n'est pas parce qu'existe désormais une flèche
f entre A et B (A => B) qu'on a pour autant f = j o g o i.
Le point que je soutiens, c'est donc que f j o g o i
On peut alors se demander : mais à quoi bon théoriser
ou formaliser s'il y a un tel abyme infranchissable entre ces
diffé-rents ordres de pensée ? La réponse
(positive) me paraît sim-ple :
1) la formalisation permet d'abord des généralisations
: on a repéré des relations musicales entre a et
b et l'on se demande si d'autres entités musicales peuvent
être ainsi reliées par cette même relation
musicale. La formalisation va pouvoir ici four-nir l'intégralité
des solutions !
2) Il y a ensuite des théorèmes d'existence : on
se demande s'il existe des entités musicales ayant telle
ou telle propriété. Le détour par la formalisation
peut alors apporter une réponse positive ou négative.
3) Il y a enfin un troisième cas, plus rare : le détour
par la for-malisation peut amener à suggérer l'existence
d'un lien « musical » entre a et b puisque A et B
sont, dans la théorie, reliés par une déduction.
Ce lien peut n'être pas musicalement évident. Il
peut même être entièrement nouveau. La formalisa-tion
peut ainsi poser des questions à la musique et non plus
simplement, comme dans les deux cas précédents,
lui fournir des réponses (soit qu'elle lui ait fourni une
généralisation, soit qu'elle l'ait convaincu de
l'existence ou de l'inexistence d'une solution). Un exemple de
ces nouvelles questions découle me semble-t-il de la théorie
de Vusa qui nous a été présentée.
En résumé, les limites musicales de la formalisation
ma-thématique tiennent au fait que les diagrammes qu'elle
met en jeu ne sont jamais commutatifs : les ordres de pensée
convo-qués restent radicalement disjoints, sans suture
possible et sans isomorphie concevable.
Ceci ne rature aucunement l'intérêt et la puissance
propre d'une théorie mathématique de la musique
mais délimite seu-lement son terrain propre d'effectivité.
Emmanuel Amiot
La question soulevée par F. Nicolas est fort intéressante
et je crois qu'il est constructif de contester les réponses
qu'il y donne !
Il y a un efficace des mathématiques, en musique comme
ailleurs, qui à mon sens ne soulève aucune interrogation
particulière (si l'on accepte bien sûr la thèse
que les mathématiques sont l'ontologie). Mais à
dire vrai, dans ce cas les mathématiques ne sont pas exactement
une formalisation. Elles sont plutôt le cadre de pensée
ontologique dans lequel sont ressaisies les propriétés
de tel ou tel type d'étants particuliers
Ceci me paraît contestable : M. Jourdain ne fait pas
vrai-ment de la prose tant qu'on ne lui a pas expliqué
ce que c'est que la prose (d'où le comique de situation).
Vouloir se servir des mathématiques en tant qu'elles
sont une lecture efficace d'un réel est un acte fondateur
en soi. Cela ne signifie d'ailleurs nullement qu'on accepte qu'elles
soient le langage incontournable et préexistant
à l'analyse du réel (comme c'est le cas en physique)
mais c'est le choix d'un mode de pensée (que l'on peut
opposer ou conjoindre à d'autres...).
Je soutiendrai pour ma part que ce diagramme étagé
n'est pas plus commutatif que le précédent et qu'il
ne résorbe aucunement les abysses existant entre ces trois
ordres : ni le premier étage (a-A-B-b) n'est commuta-tif...
Je sens ici comme un paralogisme. On n'a pas encore défini
clairement comment se fondait cet étage intermédiaire
et déjà on l'accuse de ne pas remplir son rôle
!
Je laisse à Guérino Mazzola le soin de citer le
théorème de factorisation qui laisse espérer,
au contraire, qu'il existe un objet universel remplissant l'étage
intermédiaire en rendant le premier étage commutatif
(réflexion faite, on doit pouvoir rendre le deuxième
commutatif aussi, mais pas les deux simul-tanément).
Je crois que l'opinion de F. Nicolas est fondée si l'on
considère que la couche intermédiaire du modèle
est une don-née extrinsèque, mais qu'elle ne l'est
plus si l'on prend la pré-caution de la limiter à
des échanges cohérents avec la mathé-matique
au dessus, ce qui doit être le cas si l'on fait, purement
et simplement, une modélisation au sens rigoureux du terme.
La réponse à la question reste donc ouverte à
interprétation, ce qui est la moindre des choses, vue la
musicalité du sujet...
François Nicolas
Ma thèse (non-commutativité des diagrammes
entre théo-ries musicienne-mathématique et musique)
semblant ne pas emporter une adhésion immédiate,
je dois ajouter un argument spécifiquement musical, argument
me semble-t-il de fait (mais il est clair qu'on ne peut que se
disputer sur l'existence des faits : les faits n'ont nulle évidence
intrinsèque ; seule une problématique donnée
constitue en faits pertinents telle ou telle catégorie
du « ce qui advient ». C'est bien ce que dit Rousseau
au début de sa dissertation : « Commençons
par éliminer tous les faits » pour nous mettre
à penser...).
Cette réserve préalable étant posée,
je me lance.
I. Il me semble patent que le détour par la théorie
1) n'assure nullement que la musique ainsi « produite »
soit « bonne » (même quand cette théorie
est pourtant musicienne et non pas mathématique) ;
2) n'assure même nullement que la théorie musicienne
ainsi produite soit elle-même bonne (quand le détour
se fait par une théorie mathématique) Ceci n'est
nullement une attaque en règle contre le principe d'une
théorie mathématique (mes actes et mes positions
suffisent, je pense, à attester du contraire) mais seulement
une entreprise de délimitation. Je rappelle que le principe
de notre séminaire est précisément d'interroger
les rapports mathématiques-musique (et pas seulement de
les faire « fonctionner ») en se demandant (d'où
le requisit de la philo-sophie) quand est-ce que ça marche
et quand est-ce que cela ne marche pas, et surtout pourquoi l'un
et pourquoi l'autre ?
Je reviens à mon constat, avivé par la journée
Viéru : la musique engendrée par une stricte formalisation
mathématique reste souvent infra-musicale. La question
que je pose est alors celle-ci : comment se fait-il que ce type
de théorisation pro-duise une musique si « problématique
» ?
La réponse, à mon sens, est celle-ci : parce que
les dia-grammes ne sont pas commutatifs ! C'est-à-dire
parce que les déductions propres à la formalisation
ne garantissent en aucun cas l'existence de relations musicales
pertinentes !
Si les diagrammes étaient commutatifs, on devrait engen-drer
ainsi des relations musicales valides, ce qui n'est guère
le cas si bien que ces détours, lorsqu'ils sont considérés
comme commutatifs, ne font parfois qu'habiller une impuissance
musi-cale.
Dans quelles conditions ces détours peuvent-ils au contraire
augmenter la puissance musicale ? C'est ce que pour ma part je
cherche sous l'hypothèse précisément que
cela ne commute pas et donc que le musicien n'est aucunement dispensé
d'évaluer musicalement ce que le diagramme lui offre comme
nouvelles relations possibles.
N'ai-je pas ainsi produit une sorte de démonstration par
l'absurde de ce que les diagrammes ne commutent pas ? En résumé
: s'ils commutaient, ils devraient engendrer de la bonne musique.
Ne le faisant pas, c'est en fait parce qu'ils ne com-mutent pas.
II. Au passage, j'ajoute une seconde question qui me sem-ble
essentielle en cette affaire de formalisation mathématique
: celle de l'articulation de l'algébrique et du topologique.
De quoi s'agit-il ? On ne compose pas de la « bonne »
mu-sique simplement par des opérations combinatoires, algébri-ques
et sans tenir compte de la topologie sonore. C'est un peu comme
si un compositeur tonal composait avec le seul agen-cement de
fonctions harmoniques (I, V, II...) sans s'occuper des notes de
passage, des retards, des voix, des registres... Le problème
est que faire de la musique à partir d'une algèbre,
c'est composer une topologie compatible avec cette algèbre,
et qui peut alors localement tordre (déformer) cette algèbre.
Je soutiens donc ici la thèse qu'on ne compose pas unique-ment
avec une algèbre mais en croisant topologie et algèbre.
Cela s'entendait dans le Psaume de Vieru, qui était
(malheu-reusement !) composé avec des dynamiques elles-mêmes
trai-tées de manière combinatoire mais par contre
avec des phrasés (donc une topologie) rajoutés «
à la main » pendant que les durées restaient
conçues comme un train monotone de noires parsemé
de quelques blanches... Ces problèmes touchent à
l'algèbre topologique (plutôt qu'à la topologie
algébrique). Je suggère que les formalisations proposées
tentent plus souvent d'accéder à ce rivage.
Je ne prétends pas qu'une formalisation passant par l'algèbre
topologique serait plus commutative (j'en maintiens l'impossibilité,
quitte à m'attirer les foudres des autres mem-bres du séminaire)
mais seulement qu'elle aurait plus de chance d'intéresser
les musiciens en leur proposant de possibles « nouvelles
» relations musicales.
Bernard Desroches
Construire un être mathématique et composer
de la musi-que, ce n'est évidemment pas la même chose.
Si cela était, cela supposerait que la formule mathématique
peut en quelque sorte jouer un rôle de grammaire générative
(au sens chomskyen) de la musique ou tout au moins d'une partie
de ce que nous nom-mons « musique ».
Or, comme pour la langue, ce qui fait que nous pensons «
c'est de la musique », c'est le moment où nous saisissons
la création singulière d'une forme. Cette forme
peut être valable-ment générée selon
les règles positives et négatives existantes de
la langue, mais ce qui importe surtout, c'est qu'elle surgisse
de façon inédite dans sa grammaire, nous surprenant,
emportant notre adhésion. Forme confirmant cette langue
du fait même qu'elle l'excède ou qu'elle la transforme,
même minimalement, mais dans l'inédit, pas dans le
« reproduit ». Ainsi toute interprétation est
« musicale » si et seulement si elle comporte une
création c'est-à-dire si et seulement si l'interprète
y applique son art, singulier à chaque moment. L'idée
serait donc celle d'un être mathématique capable
de confirmer la production d'une forme musicale en dépassant
(en permettant de repenser et de recalculer) en quelque sorte
l'algorithme de sa génération.
Nous disons : « c'est de la musique » lorsque nous
repérons que la création a été à
l'oeuvre dans l'oeuvre, et non en tant que forme prévisible
ou calculable, lorsque cette forme nouvelle atteste de ce qu'elle-même
produit une nouvelle forme où la mathématisation
de départ est transcendée (ou niée).
Gérard Assayag
François Nicolas : N'ai-je pas ainsi produit une sorte
de démonstration par l'absurde de ce que les diagram-mes
ne commutent pas ? En résumé : s'ils commutaient,
ils devraient engendrer de la bonne musique. Ne le fai-sant pas,
c'est en fait parce qu'ils ne commutent pas.
Sauf que ce ne sont pas les diagrammes qui engendrent la musique.
Le dernier niveau de ton second schéma, que tu ap-pelles
« musique », n'est pas une théorie reliée
au niveau supé-rieur par une relation de modélisation.
C'est un parcours parti-culier, par le compositeur, de l'ensemble
de relations contenues en puissance dans la modélisation
(musicienne-mathématique). Ce parcours est de surcroît
projeté dans un univers plus vaste que celui du modèle
(la mise en temps, l'orchestration, etc., qui, mal foutus, peuvent
détruire sans problème ce qui faisait l'intérêt
du formalisme, de même qu'on peut produire des théo-rèmes
parfaitement inintéressants dans un cadre théorique
riche par ailleurs). Un formalisme très puissant dans les
mains d'un compositeur médiocre donnera des objets musicaux
médiocres.
On ne pourrait déduire une propriété (méta-)
logique du modèle à partir d'un jugement sur la
musique résultante que si cette dernière était
régie dans tous ses aspects par le modèle, ce qui
n'arrive théoriquement que dans la musique algorithmique
(la musique intégralement générée
par ordinateur).
François Nicolas
On peut produire des théorèmes parfaitement
inintéres-sants dans un cadre théorique riche par
ailleurs. [...] On ne pourrait déduire une propriété
(méta-) logique du modèle à partir d'un jugement
sur la musique résultante que si cette dernière
était régie dans tous ses aspects par le modèle,
ce qui n'arrive théoriquement que dans la musique algorithmique.
D'accord pour cette comparaison et pour cette limitation.
Il est clair que mes formulations étaient un peu (trop
?) à l'emporte-pièce, pour relancer la question.
Car question il reste bien : tout cela commute-t-il (au sens de
la théorie des catégo-ries) ou ne commute-t-il pas
? That is the question...
Guerino Mazzola
Le second diagramme de François Nicolas n'est pas
inclus dans une catégorie car jusqu'à ce point je
n'ai pas vu / enten-du / compris des morphismes correspondant
aux flèches hori-zontales. Moreno Andratta ne l'a pas explicité
dans ce langage. Donc : d'abord la précision, après
seulement les conclusions !
Secundo : Je proposerais plutôt un diagramme commutatif
(si l'on peut y arriver !) ou la flèche verticale de droite
serait aussi de haut en bas. Ceci changerait fondamentalement
le caractère impératif du diagramme.
Mais encore, il faudrait d'abord définir des flèches
de caté-gories ! Ceci est fort important vu que ta conclusion
est très forte. Elle dépend donc d'un travail de
précision conceptuelle après lequel tout pourrait
fort bien s'écrouler en poussière...
François Nicolas
L'intérêt du débat sur la commutativité
tient, à mon sens, à la possibilité qu'il
aide à clarifier les grandes orientations de pensée
en matière de rapports entre mathématiques et musique.
Il peut indiquer (cerner) ces orientations. Il ne s'agit pas qu'à
proprement parler il les « théorise ».
Sous ce rappel méthodologique, je propose de discerner
trois positions et non pas deux :
1) La position « spontanée » des mathématiciens
(« spontanée » ici au sens où par exemple
Althusser pouvait dire que la philosophie spontanée des
scientifiques était aristo-télicienne) : les diagrammes
commutent, tout particulièrement entre les théories
musicienne et mathématique. Plus largement, ça commute
un peu partout.
2) Ma position : cela ne commute jamais, non seulement entre musique
et théorie musicienne, mais, plus fortement en-core, entre
théorie musicienne et théorie mathématique.
Je précise au passage que j'examine ici l'hypothèse
d'une théorie mathématique de la musique. Je laisse
donc de côté une autre orientation (la mienne, plus
profondément) qui est que la mathématique n'a pas
nécessairement à constituer une théorie (mathématique)
de la musique et qu'on peut se contenter de penser ses rapports
à la musique sous le signe des rapports de l'ontologie
à une ontique donnée (ces rapports ne sont alors
nullement ceux d'une théorie à son modèle).
3) Il y aurait une troisième position, et c'est à
celle-là que je veux ici en venir, position qui découle
somme toute du théo-rème d'Henkin en théorie
des modèles lequel dit (en substance) que si une théorie
est cohérente, alors elle admet un modèle (on démontre
en effet qu'il est possible de lui construire un modèle
à partir de la théorie formelle elle-même).
On peut alors soutenir qu'à partir d'une théorie
mathémati-que, formellement constituée, on va lui
construire un modèle tel qu'il soit doté, par
construction, de relations entre ses ter-mes définis
précisément par la commutation du diagramme. L'idée
est qu'on construit A à partir de a et de même B
à partir de b en sorte qu'on définit la flèche
f comme composée j o g o i. Dans ce cas, le diagramme entre
théorie et modèle commute bien par construction.
Le point me semble qu'on a ainsi construit ce que la théorie
des modèles appelle un modèle « pathologique
», qu'on pourrait appeler ici modèle formel ou formaliste,
qui n'est pas en tous les cas le modèle musical «
originel », c'est-à-dire celui retenu pour guider
la construction de la théorie mathématique.
Le problème devient alors : quel rapport y a-t-il entre
les deux modèles : entre le modèle musical «
originel « et le modèle « pathologique »
construit ?
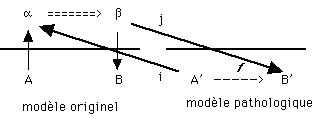
Je soutiendrai volontiers que la commutativité obtenue
sur le modèle « pathologique » ne transite
nullement vers le mo-dèle « originel ». Qu'est-ce
que ce modèle pathologique (pour lequel le passage par
la théorie mathématique commute) peut apprendre
du modèle originel ? Telle est la question obscure, car
ce modèle pathologique apprend moins sur le modèle
origi-nel que sur la théorie mathématique en question
!
On pourrait thématiser les choses ainsi : les rapports
entre les deux modèles d'une même théorie
seront dits de type méta-phorique car les deux modèles
s'avèrent « isomorphes » (un modèle
est « comme » l'autre, en un sens du « comme
» préci-sé par la théorie en jeu) alors
qu'à l'inverse les rapports entre deux théories
différentes pour un même modèle seront dits
de type métonymique...
En résumé, ce débat distribuerait trois
orientations de pen-sée quant à une éventuelle
théorie mathématique (de la musique ou d'une théorie
musicienne donnée) :
1) la commutativité généralisée,
2) la non-commutativité (par coupure radicale et change-ment
d'ordre entre modèle et théorie),
3) un mixte tordu dont il resterait alors à établir
comment sa torsion peut être féconde.