Avec cette huitième leçon, nous achèverons notre cycle consacré aux mathématiques modernes précantoriennes (1827-1858 : Gauss-Cauchy-Galois-Hamilton-Riemann-Dedekind).

La théorie riemannienne des variétés constituant un envoi de toute la géométrie moderne et contemporaine, nous ne pourrons qu’y introduire : des trois dimensions cumulatives (topologique, différentielle et géométrique) qui structurent cette théorie, nous n’examinerons en détail que la première, nous contentant ensuite d’esquisser les deux autres.

Nous conclurons alors ce cycle par une caractérisation synthétique de ces mathématiques modernes précantoriennes selon six traits distinctifs.

Surfaces de Riemann et variétés

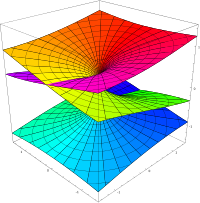
Surface de Riemann de la racine cubique complexe

Gauss→Riemann

Riemann radicalise l’ouverture vers la géométrie moderne que Gauss a opérée en 1827 : lorsque ce dernier avait dégagé une notion intrinsèque de courbure (qui ne dépendait plus d’un regard en extériorité sur la surface considérée, d’un point de vue de Sirius), Riemann vient caractériser les surfaces de manière désormais entièrement immanente en abolissant l’idée même d’un espace ambiant conçu comme théâtre passif d’activités en surface : la surface n’est plus un monde (en 2D) contenu dans un univers plus vaste (en 3D) mais un univers à elle toute seule.

Pour cela, il cumule trois gestes :

1) il radicalise le geste de Gauss en substituant intégralement une formalisation paramétrique (intrinsèque) à l’ancienne formalisation fonctionnelle (extrinsèque) des surfaces ;

2) il généralise les surfaces à deux dimensions aux hypersurfaces à n dimensions ;

3) il adjoint des atlas intrinsèques aux (hyper)surfaces pour les étendre en des variétés.

Idée directrice

La démarche de Riemann s’appuie sur le fait moderne que les fonctions complexes viennent systématiquement mettre à l’ordre du jour des fonctions multiformes (fonctions à plusieurs résultats, contrairement aux fonctions uniformes classiques). Riemann propose alors de remplacer les différentes surfaces d’une même fonction multiforme par une seule surface plurielle (dite de Riemann) devenue uniformément paramétrable : autrement dit, une pluralité de surfaces est remplacée par une surface plurielle (l’unité arithmétique d’une pluralité numérique mute en l’unité géométrique d’une surface à plusieurs couches).

Cette surface de Riemann pourra alors, à certaines conditions, être dotée d’un atlas endogène en sorte de devenir une variété proprement dite (Mannigfaltigkeit).

Trois grandes étapes

Nous étudierons la théorie des variétés selon leur caractérisation contemporaine (la clarification théorique a pris un siècle) comme étant des (hyper)surfaces topologiques, lisses et métriques.

Nous prendrons d’abord le temps de détailler ce que « variété topologique » veut dire : c’est un « espace topologique séparé à base dénombrable et localement euclidien ». Puis, nous esquisserons les deux grandes étapes suivantes :

- l’infinie différentiabilité autorisant de doter ces variétés d’un ensemble de cartes dénommé atlas ;

- la donation ultime d’une métrique (via un produit scalaire formalisant le jeu de la règle et du compas sur cet espace) caractérisant une géométrie intrinsèque.

Variétés « topologiques »

La topologie constituant le langage moderne de l’analyse, nous nous y attarderons avant d’examiner comment elle intervient dans la constitution d’une variété topologique.

Les voisinages

Des quatre manières équivalentes de définir une famille topologique de parties sur un ensemble donné (par les ouverts, les fermés, les voisinages et les adhérences), nous privilégierons la définition par les voisinages car celle-ci

1. est plus intuitive,

2. caractérise le local en l’arrimant à un point central ;

3. et s’accorde ainsi mieux à nos interprétations intellectuelles (la figure du point subjectif à fidèlement tenir y est en effet centrale).

Portée logique

Nous examinerons au passage la portée proprement logique des considérations topo-logiques précédentes puisque l’algèbre moderne formalise :

- l’opposition des contradictoires (respectant les deux principes de non-contradiction et du tiers exclu) selon l’algèbre de Boole des parties (le contradictoire d’une partie est sa partie complémentaire) ;

- l’opposition des contraires (ne respectant que le principe de non-contradiction) selon l’algèbre de Heyting des ouverts (le contraire d’une partie est le plus grand ouvert disjoint) ;

- l’opposition des subcontraires (ne respectant que le principe de tiers exclu) selon l’algèbre de Brouwer (ou de coHeyting) des fermés (le subcontraire d’une partie est le plus petit fermé complémentant).

Autres notions topologiques

Nous profiterons alors de l’axiomatisation topologique des voisinages pour avancer notre propre axiomatisation topologique de la notion de région, médiation décisive dans la dialectique du local et du global.

Nous continuerons en dégageant, sur cette base topologique, les notions de limite et de continuité.

Nous aboutirons ainsi à la notion d’homéomorphisme (bijection bicontinue) ce qui nous permettra de dégager des classes d’équivalence entre application continues (homotopie) ou linéaires (homotopie) sur ces espaces. Mais à ce stade, on n’aura pas encore de calcul différentiel et intégral (une différentielle n’est pas invariante par homéomorphisme). D’où la suite.

Variétés lisses

Si l’on suppose que les homéomorphismes précédents sont infiniment différentiables (difféomorphismes C^∞), on pourra adjoindre à la variété topologique un ensemble de cartes dénommé atlas. Avec cela, on disposera également des notions d’immersion et de plongement, d’orientabilité et de parallélisabilité, mais on n’aura pas encore de courbure (la différentielle ne présuppose pas de métrique).

Variétés de Riemann proprement dites

D’où la dernière étape dotant la variété lisse précédente d’un produit scalaire qui la géo-métrise (en la nantissant de distances et d’angles intrinsèquement définis) et lui confère des propriétés métriques intrinsèques (dont la courbure).

Interprétation intellectuelle

La portée intellectuelle de cette formalisation mathématique se concentrera pour nous sur les questions suivantes : qu’est-ce qu’un espace intrinsèque de pensée et comment y constituer un point d’intervention susceptible de composer différentiellement le lieu régional d’une action restreinte à ambition globale ?

On rehaussera l’actualité de ces interrogations pour les différentes modernités contemporaines, confrontées à l’incessant travail de sape des déconstructions postmodernes.

Traits distinctifs de la première modernité

Nous conclurons cette année par un bilan synthétique de la modernité mathématique pré-cantorienne en la caractérisant par six traits distinctifs (au regard des mathématiques classiques qui les ont précédées).

1) La modernité mathématique [Gauss-Riemann…] découpe des situations (totalisations partielles intrinsèquement autonomes) comme lieux de travail pour la pensée mathématique sans passer par l’hypothèse classique d’une vaste Totalisation préalable.

2) La modernité mathématique [Dedekind…] invente une nouvelle manière de révolutionner une situation donnée, non plus simplement par abandon-déplacement ou destruction-reconstruction mais par adjonction-extension endogène.

3) Pour l’algèbre moderne [Galois…], les groupes sont constituants de leurs éléments et non plus (comme dans l’algèbre classique jusqu’à Lagrange) constitués par eux : métaphoriquement dit, l’organisation moderne relève d’un groupement créateur de ses membres, non de la sélection d’individualités préexistantes pour former un collectif (une « équipe » !).

4) Pour la mathématique moderne [Cauchy-Hamilton…], il convient de penser une situation du point de ses possibilités et de ses potentialités, et pas seulement (position classique) de ses effectivités (de ses « faits »).

5) L’action moderne [Cauchy…] se concentre sur sa dimension régionale ou restreinte (conçue comme médiation dialectique entre le local et le global).

6) Plus globalement, la modernité mathématique privilégie la pensée en intériorité sur la pensée en surplomb, l’immanence des causes internes sur la transcendance de causes externes.

Prolongement…

In fine, nous esquisserons une prolongation de ces leçons centrée désormais sur la géométrie différentielle et pas seulement sur la géométrie algébrique.