|
François Nicolas : Leçons de mathématiques modernes |

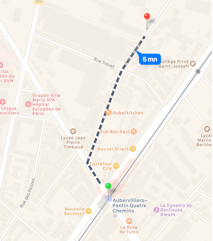
Théâtre La
Commune d’Aubervilliers - salle des Quatre Chemins
41, rue Lécuyer — 93300.Aubervilliers (M°
Quatre Chemins)
Un
dimanche par mois de 17h à 19h.
Entrée libre
(50 places)
Chaque
séance sera ensuite visionnable sur la
chaîne Youtube consacrée à ces leçons.
Site : www.entretemps.asso.fr/Nicolas/mathsmodernes
Liste de discussion : mathsmodernes@framalistes.org
Ces
leçons s’adressent à quiconque. Nulle connaissance mathématique spéciale n’est
préalablement requise. Ainsi, l’impératif de David Hilbert (1900) sera le
nôtre : « Une théorie mathématique doit être rendue tellement
claire qu’on puisse la faire comprendre au premier individu rencontré dans la
rue. »
***
|
Programme
2021-2022 ·
3 octobre 2021 : introduction ·
21 novembre 2021 : théorie
arithmétique des nombres réels (Dedekind,
1858) · 5
décembre 2021 : théorie
algébrique des groupes (Galois,
1830) · 9
janvier 2022 : théorie
des grandeurs complexes · 6
février 2022 : théorie
analytique des fonctions complexes (Cauchy,
1838) · 20 mars
2022 : théorie
algébrico-géométrique des quaternions
(Hamilton, 1843) ·
3 avril 2022 : théorie
de la géométrie intrinsèque des
surfaces (Gauss, 1827) ·
22 mai 2022 : théorie topologique des variétés (Riemann, 1854) |
Argumentaire
général de ces leçons
Leçon
n°1 – Introduction générale
- Texte
de la leçon
- Vidéo
Leçon
n°2 – Théorie arithmétique des (nombres) réels par Dedekind (1858)
- Texte
de la leçon
- Vidéo
Leçon
n°3 - Théorie algébrique des groupes par Galois (1830)
- Texte
de la leçon
- Vidéo
Leçon
n°4 – Théorie des grandeurs complexes
- Texte
de la leçon
- Vidéo
Leçon
n°5 – Théorie analytique des fonctions complexes par Cauchy (1838)
- Texte
de la leçon
- Vidéo
Leçon
n°6 – Théorie des quaternions par Hamilton (1843)
- Texte
de la leçon
- Vidéo
Leçon
n°7 – Théorie de la géométrie intrinsèque des surfaces (Gauss, 1827)
- Texte
de la leçon
- Vidéo
Leçon
n°8 – Théorie des variétés (Riemann, 1858)
- Texte
de la leçon
- Vidéo
*****