Raisonance musique/mathématiques : l’écriture en partage.

Séminaire « Musique & mathématiques »

(Ens, 19 février 2005)

François Nicolas

Résumé

On rappellera d’abord brièvement différentes manières de rapporter les mathématiques à la musique : on distinguera pour ce faire trois genres, sept espèces et dix sous-espèces.

Parmi ces dernières, on exhaussera la fiction, ou logique du « comme si » : la pensée mathématique y dispense en effet un éclairage rasant (et non pas frontal, comme dans les théories mathématiques de la musique) susceptible de faire ressortir, dans un domaine bien choisi, des aspérités et singularités musicales inaperçues par le regard musicien artisanal.

On soutiendra ensuite que, par-delà les rapports précédents, musique et mathématiques entretiennent une affinité élective, et ce pour deux raisons :

D’abord elles partagent un même souci logique, qu’elles déploient en deux problématiques orthogonales. On comparera à ce titre le rôle joué par la démonstration dans la pensée mathématique à celui joué par le développement dans la pensée musicale.

Ensuite, musique et mathématiques sont deux pensées « à la lettre », intérieurement normées par leur propre dispositif d’écriture, ce qui constitue une singularité absolue parmi les différents types de pensée.

On esquissera alors le programme possible d’un penser l’écriture musicale à la lumière de l’écriture mathématique.

On fera à ce titre l’hypothèse d’un double chiasme entre ces deux types d’écriture :

l’écriture mathématique utilise une même lettre pour différentes opérations là où l’écriture musicale utilise différentes lettres pour une même opération (d’où une redondance singulière que Rousseau proposera d’amender en arithmétisant le solfège…) ;

la mathématique utilise différentes inscriptions pour une même chose là où la musique utilise la même inscription pour plusieurs choses (d’où les problématiques, proprement musicales, de transposition, d’arrangement et de transcription…).

Ainsi les lignes de partage lettre claire / lettre obscure s’avèreraient duales entre musique et mathématiques.

S’il est vrai que tout ceci met en œuvre une dialectique du sensible et l’intelligible, on conclura sur l’intérêt d’associer la philosophie aux rapports musique-mathématiques en sorte de réactiver le vieux nœud grec à trois, quand les raisonances musicales accompagnaient la naissance tant de la philosophie (Parménide) que de la mathématique comme raison et plus simplement comme calcul (invention de la démonstration via la création du raisonnement par l’absurde).

–––

L’exposé d’aujourd’hui, faisant intervenir la « raisonance  » entre musique et mathématiques (par un jeu de mots sur la résonance et l’idée que la raison est mobilisée en cette affaire), vise à soutenir sur musique et mathématiques un point de vue un peu particulier : la musique a gagné à essayer de penser son activité avec les mathématiques sans pour autant être dans la modalité la plus classique du rapport en musique et mathématiques, qui est celle du calcul. Si cette dernière est bien légitime, il s’agit ici de défendre un autre rapport aux mathématiques que celui qui n’a pour but que de fournir la musique en formules de calculs.

Plan

I. Des manières de rapporter musique & mathématiques

3 genres, 7 espèces et 10 sous-espèces

Intérêt de la fiction :

ex. audition musicale & intégration mathématique

(modèle musical fictif d’une théorie mathématique)

II. Une affinité élective, pour 2 raisons :

un souci logique

une pensée à la lettre

III. Penser l’écriture musicale avec les mathématiques

L’hypothèse de deux chiasmes

Je rappellerai dans un premier temps ce qui a déjà été dit sur ces rapports musique-mathématiques dans un séminaire antérieur (mamuphi) de manière à déployer, à l’intérieur de cet espace des possibles, la modalité particulière que je voudrais privilégier aujourd’hui. À cette occasion, je voudrais thématiser les raisons que l’on peut avoir de penser qu’il se passe entre musique et mathématiques quelque chose de singulier, voire qu’elles ont quelque chose en partage de tout à fait singulier. Je soutiendrai à ce titre la double thèse qu’elles ont en commun un souci logique et une pratique de l’écriture. Puis, et ce sera l’élément le plus nouveau de cet exposé, j’essaierai de thématiser la question de l’écriture en partage.

Différentes manières de rapporter les mathématiques à la musique…

Il s’agit ici de rapporter les mathématiques à la musique d’un point de vue subjectif de musicien.

Les mathématiques peuvent-elles intéresser le musicien d’une manière ou d’une autre ?

Je distingue trois manières générales de répondre :

· Première manière : il n’y a pas de rapport entre les deux.

· Deuxième manière : il ne peut y avoir de rapport que médié par un troisième terme ; il n’y a donc pas de rapport immédiat.

· Troisième manière : il y a un rapport immédiat, sans convocation d’une discipline tierce.

D’où le tableau suivant :

				Symétrie ?	Inverse ?
0. Il n’y a pas de rapport
Médiat (le rapport se joue à trois)	I. Médiation scientifique ou artistique	1. Médiation ontique	Essentiellement physico-acoustique	Non	Non : Ma ®Mu
		2. Médiation imaginée	2a. avec une autre science	Non	Non
			2b. avec un autre art
	II. Médiation philosophique	3. Contemporanéité		Oui	Phi Ma ÛMu
Immédiat	III. Inspiration : raisonances	4. Métaphore / Analogie (« comme »)		Non	Oui	®musique
						®mathématiques
		5. Fiction (« comme si »)		Non	Non
	IV. Formalisation	6. Formalisation		Non	Non
	V. Informatique	7. Application (calcul)		Non	Non
		8. Conditionnement (logique)		Non	Oui	®musique
						®mathématiques
	VI. Intersection	9. Inclusion		Non	Non

Dans chacun des cas, je pose la question de savoir s’il y a une symétrie de ce rapport : rapporter les mathématiques à la musique ne veut pas forcément dire, en effet, que ce rapport sera symétrique. Je pose alors la question : qu’est-ce qui se passe, pour ces différents cas, dans l’autre sens ?

Je ne vais guère détailler tout ceci, mon propos aujourd’hui étant simplement de situer mon espace de travail.

Concernant la manière I, divisée entre nature scientifique ou artistique de la médiation, la proposition la plus spontanée est de rapporter musique et mathématiques via la physique (l’acoustique). Cela revient à considérer que la musique a comme matériau un matériau sonore lequel relève de la physique, laquelle est mathématisée depuis Galilée, d’où s’en suit qu’il y a bien un rapport (médié) entre musique et mathématiques. Il s’agit d’une médiation qu’on peut dire ontique au sens de la distinction heideggerienne entre ontologie (concernant l’être en tant qu’être) et ontique (concernant l’étant).

La modalité II, nommément la médiation philosophique, me paraît tout à fait importante. Elle est indexable à ce que j’appelle la figure de la contemporanéité, selon l’idée que la philosophie elle-même a comme tâche particulière de penser la contemporanéité de ces différentes formes de pensées qu’Alain Badiou appelle les procédures de vérité, en l’occurrence entre la pensée mathématique et la pensée musicale. Pour autant qu’il y ait un temps de la pensée, c’est-à-dire pour autant qu’il y ait un présent, la philosophie aurait comme tâche singulière de ressaisir ce qui est le présent de la pensée et par là de caractériser ce qu’il en est du contemporain. C’est par exemple une préoccupation importante pour Boulez : quand celui-ci essaie d’établir sa théorie de la musique aujourd’hui, il veut être dans une modalité contemporaine (et non pas archaïque) du penser la musique.

Où l’on voit l’intérêt intrinsèque d’organiser ce séminaire à trois : la philosophie mérite d’être présente dans ces rapports musique et mathématiques à mesure de ce que cette modalité philosophiquement médiée me semble à privilégier, sans prétendre pour autant à l’exclusivité.

Concernant les rapports cette fois immédiats entre musique et mathématiques, sans discipline tierce donc, j’en distingue quatre modalités :

1- l’inspiration ou les raisonances (que je vais ensuite détailler) comporte deux sous-espèces : métaphore/analogie et fiction ;

2- la formalisation, où cette fois les mathématiques formalisent le domaine musical (un certain nombre de thèmes que Moreno Andreatta a présentés ce matin rentrent dans ce cadre) ;

3- la modalité informatique qui renvoie soit à la modalité du calcul (lorsque des résultats mathématiques peuvent s’appliquer à la musique), soit à une modalité de conditionnement plus strictement logique ;

4- pour mémoire, et cela relève pour moi plutôt de la tératologie, je distingue enfin la modalité dite de l’intersection qui consiste à considérer que mathématiques et musique auraient une intersection commune. Tom Johnson ainsi soutient quelque chose d’équivalent, à savoir que pour lui, dans certaines conditions du moins, on peut faire de la mu en faisant des mathématiques… Ainsi, lorsque par exemple il fait des combinatoires arithmético-algébriques, ceci selon lui suffit pour faire de la musique. Je signale que cette position existe et a sa légitimité propre, bien qu’elle me sidère un peu…

Parmi ces sept espèces et ces dix sous-espèces, je m’intéresserai plus particulièrement à la médiation philosophique et à l’inspiration/raisonances.

Différents types de théorie musicale

Pour rappel, j’indique qu’en matière de théorie musicale — si on appelle théorie musicale la théorie qui a la musique pour objet — la question est de savoir comment la chose (la musique en l’occurrence) est théorisée. Il faut donc prendre mesure du fait qu’il y a différentes sortes de théories musicales car selon les disciplines, l’objet « musique » n’est pas le même, bien que le nom soit identique.

Parmi cette variété de théories, je rehausse les théories musiciennes de la musique parmi lesquelles on peut distinguer des théories musicologistes (en figures de savoir : il y s’agit de théoriser les savoirs sur la musique qui sont nécessaires au musicien) et des théories compositionnelles ou en intellectualité musicale, qui sont beaucoup plus prescriptives : si elles sont irriguées de savoirs, elles n’ont pas comme figure principale d’être un mode d’organisation des savoirs car leur propos est prospectif. Par exemple, Penser la musique aujourd’hui de Boulez est une théorie entièrement prescriptive, qui ne se situe pas dans une logique positiviste de prétendue objectivité.

Il faut donc se rappeler qu’une théorie mathématique de la musique occupe une position tout à fait singulière dans ce panorama des théories musicales, en ce qu’elle correspond à des enjeux propres, à un mode de pensée bien circonscrit, c’est-à-dire à une caractérisation de son objet propre (on en reparlera sans doute avec Mazzola) : il est certain que dans une théorie comme celle-ci, ce qui est nommé musique n’est pas exactement la même « chose » que ce que, comme compositeur, j’appelle musique.

Métaphore/analogie/fiction

Je voudrais à présent reprendre (voir la catégorie « inspiration ») la dichotomie métaphore/analogie et fiction.

- Première modalité : la métaphore est la comparaison entre deux termes.

- Deuxième modalité : l’analogie compare cette fois deux rapports. On dira par exemple : « l’audition est à la musique comme l’intégration est à la mathématique ».

Dans ces deux cas (métaphore ou analogie) le régime du « comme » a comme caractéristique d’être relativement isolé, offrant ainsi une image locale.

- Troisième modalité : je l’appelle fiction car elle inclut un schème déductif, qui passe du comme au comme si. Là où le « comme » pose un terme ou une comparaison entre deux rapports, le « comme si » émet une hypothèse qui donne lieu à un raisonnement déductif.

Fiction

Donnons un bref exemple prélevé dans la théorie mathématique des modèles.

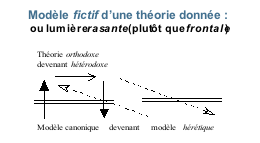
À gauche, un modèle (au sens mathématique du terme) constitue la base que l’on essaie de comprendre au moyen d’une théorie dite orthodoxe qui vise à rendre compte de ce modèle. La flèche qui monte désigne la formalisation et celle qui descend l’interprétation. Par exemple, si on essaie de rendre compte du calcul de la surface des aires, et qu’on dispose pour ce faire d’une théorie de l’intégration, on dispense ainsi une lumière frontale car cette théorie est directement destinée à éclairer le domaine particulier.

L’idée du modèle fictif revient à faire « comme si » cette théorie était à même d’éclairer un tout autre modèle, nommément le modèle hérétique. Dès lors, on obtient une lumière rasante car on fait « comme si » notre théorie, élaborée pour un domaine donné, allait pouvoir nous éclairer sur quelque chose d’autre. En logique mathématique, la pertinence d’une telle démarche a été démontrée : on prouve que toute théorie logiquement constituée (cohérente) admet un modèle hérétique en vertu du fait qu’une théorie est nécessairement finie alors que son modèle est infini.

Mon idée est alors que l’on peut utiliser les mathématiques en essayant de voir quelle lumière rasante une théorie mathématique peut porter sur un domaine musical qui n’a rien à voir. On peut, par exemple, utiliser ainsi la théorie mathématique de l’intégration à propos de l’audition musicale :

Modèle musical fictif de la théorie mathématique de l’intégration

Trois auditions…

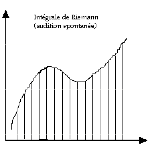
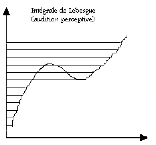
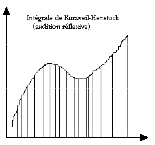
⇒ La troisième audition est la bonne !

Je distingue ici trois séquences de la théorie de l’intégration (l’intégrale de Riemann, celle de Lebesgue et celle de Kurzweil-Henstock) et j’ai montré par ailleurs comment on pouvait à partir de là éclairer de manière rasante les modalités différentes de l’audition musicale.

Dans le premier cas, j’ai distingué une audition spontanée, dans le deuxième une audition perceptive et dans le troisième une audition réflexive. J’en concluais que l’on pouvait tenir qu’il y a trois auditions qui se cumulent de sorte que, pour vraiment connaître une œuvre, il y faut trois auditions et que la troisième est ici la bonne !

Voilà un exemple où l’on se sert d’une théorie mathématique comme d’un projecteur latéral, dont l’intérêt est de nous révéler, par une lumière rasante, des aspérités que l’on ne verrait pas forcément dans le domaine musical si l’on déployait une théorie frontale. Et cela fait partie du jeu même de la lumière rasante que de voir quelles en sont les limites, car bien sûr cette théorie ne fonctionne pas exactement : il n’en reste pas moins que c’est là un usage des mathématiques qui nous aide à penser la musique avec elles.

Différentes manières de penser la musique avec les mathématiques…

On peut ainsi recenser 17 manières de caractériser la musique avec les mathématiques, et il peut y en avoir bien d’autres.

17 manières de penser la musique avec les mathématiques…

1. Penser la logique musicale (et donc l’articulation raison/calcul) avec la logique mathématique (partie II)

2. Penser le « avec » avec la théorie des modèles (partie I)

3. Penser la perception musicale avec la théorie des pavages

4. Penser l’audition avec la théorie de l’intégration (partie I)

5. Penser l’écoute musicale avec la théorie de la différenciation

6. Penser l’écoute à l’œuvre avec les jeux mathématiques de taquins

7. Penser les modalités de l’entendre avec les théories mathématiques de l’intrinsèque et de l’extrinsèque

8. Penser l’écriture et la lettre musicales avec l’écriture et la lettre mathématiques (partie III)

9. Penser l’articulation musicale entre écriture et écoute avec l’articulation mathématique (de la théorie) des ensembles et (de la théorie) des catégories

10. Penser le monde de la musique avec la théorie des topos

11. Penser la composition musicale avec les théories mathématiques du local et du global

12. Penser l’entre-œuvres des concerts avec la théorie des catégories

13. Penser la combinatoire musicale avec l’algèbre

14. Penser le style diagonal de pensée avec la procédure diagonale de Cantor

15. Penser le temps musical avec la théorie des équations différentielles (cf. A. Lautman)

16. Penser la nature musicale avec la théorie des ordinaux et cardinaux (cf. A. Badiou)

17. Penser les rapports de l’œuvre à son matériau avec la théorie des nombres surréels (cf. A. Badiou)

J’ai souligné dans ce tableau les manières que je vais aborder aujourd’hui plus en détails :

· penser la logique musicale avec la logique mathématique ;

· penser le « avec » avec la théorie des modèles — voir ce que j’ai esquissé précédemment sur la théorie des modèles — ;

· j’ai présenté aussi rapidement « penser l’audition avec la théorie de l’intégration » ;

· enfin, j’insisterai sur l’exploration du « penser l’écriture et la lettre musicale avec l’écriture et la lettre mathématique ».

Il se trouve que j’ai également utilisé cette grille pour explorer les rapports entre musique et psychanalyse.

Une affinité élective

La question reste de savoir si, par-delà ces déterminations, il y a quelque chose comme une affinité élective entre musique et mathématiques. L’expérience semble justement indiquer qu’il y en a une. On constate par exemple que beaucoup de mathématiciens font de la musique, même si l’inverse semble moins vrai. Il y a un mode de penser qui, semble-t-il, facilite les résonances entre mathématique et musique.

Je pense qu’il y a bien une affinité élective entre l’une et l’autre et je propose deux raisons à cette constatation empirique :

· un souci logique en partage,

mais deux logiques orthogonales ;

· la singularité d’une pensée à la lettre,

mais deux logiques orthogonales.

Vulgarisations comparées

On peut discerner par la négative ces deux traits en rapprochant vulgarisations mathématique et musicale.

La vulgarisation mathématique a deux caractéristiques :

· la démonstration y est oubliée (seul le résultat est donné),

· et l’écriture mathématique, dans son opacité éventuelle, y est entièrement effacée.

De même en musique :

· une vulgarisation musicale revient à oublier le développement un peu comme on élude la démonstration en mathématiques,

· et on efface là aussi la partition, avec ce qu’elle peut comporter d’opacité pour qui ne sait pas la déchiffrer.

On retrouve donc bien, dans le processus de vulgarisation, ces deux mouvements qui effacent la logique et minent l’écriture.

un souci logique

Reprenons notre première raison : musique et mathématiques ont un même souci logique, c’est-à-dire une même préoccupation quant à la logique, bien qu’il s’agisse de deux logiques distinctes.

Deux histoires

Précisons qu’en mathématiques aussi bien qu’en musique, la déduction et l’écriture correspondent à des coupures historiques importantes.

L’invention de la démonstration mathématique est essentielle, comme celle de l’écriture musicale (c’est elle qui, à mon sens, fournit à la musique la possibilité de devenir un monde). De ce point de vue, mon hypothèse est qu’il n’y avait pas d’écriture musicale pour les Grecs, mais seulement un mélange d’écriture et de notations, et qu’à ce titre, la musique pour les Grecs n’était pas la même chose que la musique pour nous, en particulier ne formait pas un « monde »..

Ces deux dimensions, aujourd’hui menacées (l’écriture musicale l’est notamment en ce qu’elle n’est plus ajustée à la matière sonore), ont connu des surgissements historiques qui ne sont pas synchrones.

Cf. Arpad Szabo : il développe le fait que, si les mathématiques babyloniennes et égyptiennes existaient bien, elles possédaient un dispositif de calcul sans avoir le souci de démontrer leurs formules. Les mathématiques sont donc véritablement nées avec les Grecs, lorsque le souci de la démonstration est apparu. Szabo montre remarquablement que ce surgissement a eu lieu à la faveur d’un nœud à trois : mathématiques, philosophie et musique. Au VI° siècle avant J.-C., le nœud qui a érigé les mathématiques comme espace de pensée et non simplement de calcul, a été adossé d’une part à la philosophie et d’autre part à la musique, qu’il a nourrie en catégories.

C’est pourquoi, si l’on veut aujourd’hui tresser quelque chose entre musique et mathématiques, on a peut-être encore quelque intérêt à considérer la philosophie.

La première démonstration recensée dans l’histoire de l’humanité selon Szabo est inscrite dans le Fragment VIII de Parménide.

Ce premier raisonnement apparaît comme un raisonnement par l’absurde, qui par définition n’est pas constructiviste, mais se fonde sur une cohérence globale : il s’agit de montrer que quelque chose est parce que son contraire ne peut pas être.

Parménide pose ici le problème de savoir si l’être est engendré. Pour démontrer qu’il ne peut pas être engendré, il montre par l’absurde que, si l’Être était engendré, il devrait l’être soit par l’Être soit par le non-Être, conformément à cette logique classique. Or il ne peut être engendré ni par ce qui n’est pas («quelle nécessité l’aurait amené à l’être s’il venait du rien ? »), ni par lui-même («s’il est né, il n’est pas »). Ces deux cas n’étant pas possibles, l’être est donc inengendré.

Notons au passage que l’idée de la démonstration mathématique vient de la philosophie !

Deux logiques othogonales

De plus, en musique et en mathématiques, sont à l’œuvre deux soucis logiques qui se réfèrent à des logiques orthogonales.

Si l’on considère en effet les trois grands principes logiques hérités des Grecs, on peut remarquer que la musique ne les pratique pas de la même manière :

· Là où la mathématique se dote du principe d’identité, la musique aurait plutôt un principe de différenciation (si en musique on répète un thème, le simple fait de le répéter fait qu’il n’est plus exactement le même du point de vue de la logique du développement ; il n’est pas simplement une reprise mais introduit déjà un principe de déplacement, ce qui correspond au fait que deux écoutes successives ne sont pas identiques).

· Au principe de non-contradiction en mathématiques, la musique opposerait un principe de négation contrainte (lorsqu’on tient une chose, on est dans l’obligation, selon une véritable logique de développement musical, de montrer la chose et son contraire ou son altérité, c’est-à-dire de ne pas garder la chose dans sa fixité, mais de confronter constamment l’existence de la chose à l’existence de son contraire ou de son altération ; aussi ne peut-on avoir une seule exposition d’une chose).

· Enfin, si la mathématique maintient le principe du tiers exclu, la musique aurait un principe de tiers obligé : non seulement on aurait la chose et son contraire, mais encore l’intervention d’un élément tiers. Jusque dans la fugue, monothématique par excellence, des éléments extérieurs interviennent ainsi dans le rapport entre le sujet et le contre-sujet.

Ainsi, la musique et les mathématiques répondent à deux logiques orthogonales, qui ne sont pas régies par les mêmes principes.

Trois modalités de développement musical

De ce point de vue, on pourrait distinguer trois modalités du développement musical :

- une figure de la déduction (exemple : Beethoven, Boulez), qui va de la partie vers le tout (une cellule se développe pour générer le tout) ;

- une figure du déploiement (exemple : Debussy, Ligeti), où on est moins dans une problématique algébrique que dans une problématique topologique, avec une réalité locale (un timbre par exemple) qui va par extension générer du global ;

- une figure d’occupation (exemple : le Cantus firmus chez Bach, Stockhausen), où une sorte d’espace global va être occupé localement.

des pensées à la lettre

Deuxième raison pour l’affinité élective entre musique et mathématiques : on a deux pensées « à la lettre ».

Soit une équation qui évoque un cercle : pour quelqu’un qui ne connaîtrait pas les mathématiques, cette écriture ne désignerait pas de manière évidente une telle figure. Il y a le même rapport d’étrangeté entre cette expression mathématique et la figure du cercle qu’entre ce qui est écrit sur une partition pour ceux qui ne connaissent pas le solfège et la réalité sonore qu’elle indexe.

De ce point de vue, je soutiens qu’il y a une double matérialité musicale et qu’il importe donc de distinguer matière et matériau. La musique a comme matériau le sonore alors que la lettre musicale, c’est-à-dire la note, a une fonction de matière (la lettre serait la figure moderne de la matière).

Dans la partition, se joue quelque chose de la matière de la musique, mais qui n’est pas son matériau. Je tiens d’ailleurs que le rapport entre la matière (littérale) et le matériau (sonore) n’est pas un rapport de représentation, contrairement à ce que l’on dit généralement : une note ne « représente » pas un son, à preuve l’écriture du silence qui a une consistance musicale indéniable mais ne représente rien. À mon sens, la note est un point dans la matérialité d’une ossature, mais il faut abandonner l’idée que l’écriture musicale serait une manière de représenter le son.

La partition musicale est une écriture, c’est-à-dire un système de lettres (le solfège) et un amas hétérogène de notations disparates.

Il faut ici bien distinguer le système d’écriture où les lettres renvoient à la note (c’est-à-dire à la hauteur et à la durée) du fatras hétérogène de notations. La partition est cet ensemble totalement impur.

Voir les deux exemples suivants où l’on distingue l’écriture seule et l’écriture avec les notations (qui est la vraie partition).

Le fatras hétérogène d’une partition

Écriture + notations :

Écriture seule :

La double écriture

Le problème supplémentaire de la musique contemporaine, c’est qu’il y a une double écriture : dans la musique mixte (pour instruments et pour électro-acoustique), on n’inscrit pas la musique de la même manière. C’est à mon sens très préoccupant : pour les instruments, on garde une écriture musicale proprement dite avec les notations traditionnelles, alors que pour l’ordinateur, on dispose de patchs (programmes informatiques), c’est-à-dire d’une inscription informatique associée à une boîte noire : on n’a plus l’intelligibilité de ce qui se passe, puisque ce n’est pas inscrit dans la partition.

Exemple : « Dans la distance »

Exemple : Duelle

Souvent, en musique contemporaine on dit qu’il y a deux mondes correspondant à ces deux types d’écriture : je récuse cette idée car à mon sens la musique forme un seul monde. Il faut ainsi considérer que ce qui vient de l’ordinateur n’est pas un autre monde mais des images sonores du même monde. Il faut donc avoir un dispositif de pensée qui tienne tout cela dans le même espace de pensée.

Penser l’écriture musicale avec les mathématiques

Mon propos va être maintenant d’éclairer un certain nombre de caractéristiques de l’écriture musicale à la lumière de ce qu’est l’écriture mathématique pour montrer ce que peut être penser la musique avec les mathématiques.

C’est là une des caractéristiques qui m’a frappé dans la théorie de l’intégration, telle que la présente Lautman dans son Essai sur l’unité des mathématiques :

Lautman montre ainsi que dans cette écriture de l’intégrale, les x occupent des fonctions différentes.

Lebesgue soutient la même proposition en la déployant, lorsqu’il montre à son tour que les x qui interviennent dans ces expressions correspondent en fait à des fonctions différentes.

Je résume tout cela dans ce tableau récapitulatif :

Dans cette présentation de l’intégrale, une même lettre occupe quatre fonctions mathématiques différentes et il est intéressant de constater qu’au fil de l’histoire de l’intégration, on va distinguer ces fonctions dont on pensait d’abord qu’elles étaient les mêmes. Une part de l’histoire de l’intégration (en particulier le passage de l’intégrale de Riemann à celle de Lebesgue) porte ainsi là-dessus.

De la sorte, une première caractérisation me paraît frappante, que j’appelle une écriture mathématique « en plis, replis et déplis » : des fonctions différentes sont repliées sur la même lettre puis s’opère un travail pour les déplier, pour distinguer ce qui est donné dans la même lettre.

Premier chiasme

D’où ma première hypothèse sur l’existence d’un chiasme entre les deux écritures musicale et mathématique : l’écriture mathématique utiliserait une même lettre pour différentes opérations et l’écriture musicale, à l’inverse, emploierait différentes lettres pour une même opération.

Je renvoie sur ce point à la réforme d’écriture qu’a proposée Rousseau en 1742-43. Rousseau en effet trouvait l’écriture musicale redondante et en suggérait une simplification.

Il propose, parmi d’autres avantages, de réduire le volume des partitions en arithmétisant le solfège. Voici son argumentaire :

Rousseau rappelle dans ses Confessions qu’il a présenté ce projet à l’Académie, qui l’a unanimement félicité, et que le seul à lui avoir fait une objection c’est de façon on ne peut plus significative Rameau…

Le fait que l’écriture musicale soit redondante est en effet l’une de ses propriétés essentielles : c’est notamment nécessaire pour pouvoir la déchiffrer facilement.

A-t-on vraiment ainsi simplifié l’écriture musicale ? Je vous en laisse juge :

Second chiasme

Je voudrais relever inversement un second chiasme : la mathématique utilise cette fois différentes inscriptions pour la même chose de sorte qu’une même idée fait l’objet de différentes formalisations.

À l’inverse, la musique utilise la même inscription pour différentes choses, c’est-à-dire une même ossaturation dans la partition pour différents corps instrumentaux.

Une inscription pour violon seul

Une inscription pour orgue et orchestre

Une transcription !

La ligne du violon a donc simplement été transposée de mi en ré : Bach est parti de la même ossaturation et il en a tiré une sorte de concerto pour orgue et orchestre, rapprochant ainsi les deux pôles instrumentaux les plus opposés concevables à l’époque.

L’idée qu’on aurait alors une dualité constitue donc une hypothèse sur laquelle je travaille.

En mathématique, on aurait une même lettre pour n opérations alors qu’en musique on aurait plusieurs lettres pour une même opération ; à l’inverse, on aurait en mathématiques plusieurs inscriptions pour une même chose alors qu’en musique on aurait une seule inscription pour plusieurs choses.

Cette idée m’a suggéré l’élaboration du schème suivant :

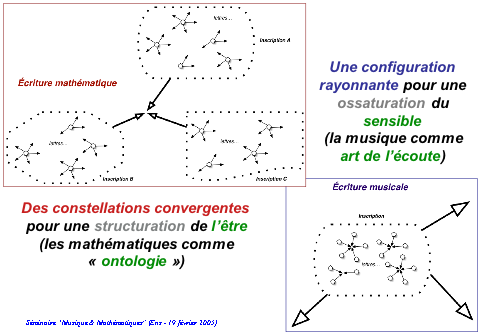
L’écriture mathématique aurait ainsi pour caractéristique d’avoir plusieurs modes d’inscription pour cerner la même réalité archaïque, alors qu’en musique, inversement, la même inscription vaudrait pour différentes réalités.

Existerait donc un rapport dual entre ces deux modes d’écriture, ce que je propose de thématiser de la manière suivante : en mathématiques, on aurait des constellations convergentes pour une structuration de l’Être (qui renvoie à la structuration des mathématiques comme ontologie selon Badiou : pour autant par exemple que le cercle serait une figure de l’être, on mobiliserait différentes constellations convergentes pour identifier cette figure), alors qu’en musique, comprise comme art de l’écoute, on aurait par opposition une configuration cette fois rayonnante pour une ossaturation du sensible.

*

Pour conclure, la question du rapport sensible/intelligible intervient non pas pour attester que le sensible serait du côté de la musique et que l’intelligible serait du côté des mathématiques (remarquons que même en mathématiques, on a un rapport sensible dans la dimension figurale). Si cette dialectique sensible/intelligible est à l’œuvre dans ces rapports entre les deux modes d’écriture, il y a toute raison de penser que la philosophie doit aussi être convoquée. S’il s’agit bien ici peu ou prou de travailler sur ce rapport musique et mathématiques, il est important de ne pas oublier la philosophie, non pas qu’elle en participe au même titre, mais parce qu’elle y tient une place singulière.

––––––––––