François NICOLAS

On peut distinguer, a priori, 36 situations différentes tenant à
* 4 moments acoustiques:
- attaque
- entretien
- extinction
- répétitions: d'attaques et de hauteurs-legato, d'entretiens (tiré-poussé...)
* 3 dispositions en matière de lutherie:
- corde à nu (scellée dans les murs)
- corde montée (chevalet + caisse/table d'harmonie)
- cordes jumelées (montées sur un même chevalet)
* 3 modalités de jeu instrumental:
- corde pincée (plectre)
- corde frappée (marteau)
- corde frottée (archet)

On examinera 14 de ces situations selon la répartition suivante:

1) Attaque:
- pincée: à nu
corde montée
- frappée: à nu
corde montée
deux cordes jumelées
- frottée: à nu
corde montée
N.B.: Il nous faudra soigneusement distinguer dans l'attaque ce qui intervient lors de l'excitation de ce qui se produit au début de la résonance; on traitera pour ce faire de quelques comportements physiques transitoires qu'adopte la corde après qu'elle a été relâchée.

2) Entretien:
Cela n'existe que pour la corde frottée (archet). On l'examinera selon deux modalités: corde à nu, corde montée.

3) Extinction:
On traitera l'extinction (par étouffoir...) selon que la corde est à nu ou montée sur chevalet + caisse/table.

4) Répétitions:
On examinera - dans le seul cas d'une corde à nu - les trois modalités: pincée, frappée et frottée.

Raisons de s'intéresser aux transitoires:
* Raisons musicales et esthétiques:
- l'articulation et le phrasé sont constamment éclairés de transitoires;
- les transitoires suggèrent une approche non substantielle du matériau musical: on y saisit le son musical moins en l'épaisseur de son corps - la résonance qui perdure en équilibre prévisible - qu'en la brièveté de son existence, en la fragilité et l'instabilité de ce qui peut à tout moment s'interrompre.
- les transitoires suscitent un abord en généricité de l'instrument: avec les transitoires un instrument est associé à ces "quelque-chose" dont on repère la présence "quelconque" sans pouvoir au sens strict les discerner (les isoler, les distinguer). On sait ainsi que, parmi les transitoires, les attaques jouent le rôle principal dans la reconnaissance des instruments alors que les transitoires afférents aux notes enchaînées legato semblent jouer un rôle plus secondaire tandis que celui des transitoires d'extinction parait rester mineur (cf. Campbell et Heller).

- le transitoire comme donnée locale

En tous ces sens, les transitoires ont donc une fonction plus musicale que sonore, une réalité plus auditive que strictement perceptive: s'ils permettent bien de percevoir l'instrument, ils ne sont pas en général eux-mêmes perçus de manière distincte; d'où qu'il s'agisse toujours, comme on le verra, "des" transitoires: en situation musicale, il est aussi difficile d'isoler "un" transitoire qu'il l'est de discerner "une" nuance d'une interprétation. Les transitoires sont la gerbe d'étincelles impalpables que trace autour de lui le son instrumental.
* Raisons techniques dans le cadre du travail actuel sur MOSAIC: la maîtrise du jeu instrumental - en particulier avec archet - suppose une bonne compréhension des mécanismes physiques et des régimes d'entretien qui, seule, peut permettre la "fonctionnalisation" ultérieure des paramètres du jeu.
* Question de méthode: il convient de ne pas se satisfaire de la position de l'utilisateur naïf qui manipule un outil en ignorance des choix (explicites ou implicites) ayant présidé à sa conception et qui pourraient alors s'imposer à lui sans distance et réflexion possibles. D'où la nécessité de tester en un point au moins (ici les transitoires de corde) le projet dans toute sa profondeur en sorte d'examiner les décisions prises en amont et par là de se forger un jugement autonome.

Remarque générale:
Le stade actuel du travail sur MOSAIC implique un rapport concomitant aux cinq dimensions suivantes:
- aspect proprement physique (mécanique et acoustique)
- implémentation informatique
* travail de lutherie
* technique d'instrumentiste
* problématique musicale.
On ne s'étonnera donc pas de trouver trace de ces cinq niveaux dans ce travail.

Cette catégorie a communément deux usages distincts et par là deux sens différents:
* Sens physique (strict) = partie non périodique d'une évolution principalement périodique. En ce sens le transitoire, quoique souvent passager, n'est pas nécessairement bref.
* Sens plus usuel = évolution très momentanée, radicalement apériodique (en particulier non "pseudo-périodique").
En ce dernier sens, plus restreint mais plus courant, l'évolution d'une corde après son temps d'excitation ne relèverait pas de la catégorie "transitoire" même si la corde étant plus ou moins amortie et inharmonique s'éloigne ainsi sensiblement du modèle périodique d'une corde idéale. De même, en ce sens restreint, la corde frottée ne relèverait de régimes transitoires qu'au moment initial de l'attaque et lors des coups d'archet (tiré-poussé...).

Dans l'usage ici proposé du mot "transitoire", je me situerai entre ces deux positions extrêmes, non par atavisme pour les positions centristes mais parce que l'usage musical du mot suggère me semble-t-il une reconsidération du problème: somme toute pour le musicien le mot "transitoire" désigne cette partie du son qui rend audible sa fragilité constitutive, qui manifeste de manière sensible son instabilité et son déséquilibre.
Pour tenter alors de fixer les idées de manière un peu plus précise, je proposerai la distinction suivante:
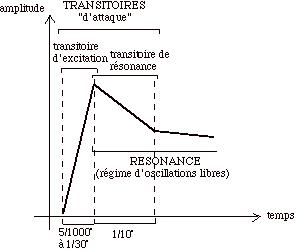
- on appellera transitoire d'excitation le phénomène sonore apériodique qui relève de la durée même de l'excitation;
- on appellera transitoire de résonance les évolutions rapides (pseudo-périodiques) qui relèvent de l'après-excitation et qui interviennent donc au cours même d'un régime d'oscillations libres.

On peut alors voir que ce que l'on appelle communément "transitoire d'attaque" s'avère englober - dans le cas de la corde tout du moins (qui est le seul ici que j'examine) - un transitoire d'excitation et un transitoire de résonance. Pour illustrer la manière dont le "transitoire d'attaque" se situe à cheval sur le temps d'excitation et sur le temps de la résonance, prenons l'exemple suivant d'une corde pincée par un plectre. Le "transitoire d'attaque" va conjoindre en réalité quatre transitoires différents:

1) le transitoire tenant à l'effet sonore qu'engendre le choc du plectre sur la corde. Ce transitoire se focalise bien sûr lors du contact (transitoire d'excitation) quoique sa perception effective implique qu'il mette en résonance la corde par delà le temps réduit de l'excitation (en l'occurrence 1/30° de seconde) et qu'il laisse ainsi derrière lui une trace de son existence, cette sorte d'ombre qu'il porte sur la résonance.
Ce transitoire dure 3/1000° à 1/30° de seconde; il est souvent très repérable.

2) le transitoire tenant à l'amortissement des vibrations de la corde; c'est là un transitoire d'après excitation qui traduit bien le sens physique du terme "transitoire". Le point décisif est que ce transitoire peut être tout à fait audible sous certaines conditions (voir plus loin). En ce cas on a bien une évolution rapide (d'un régime d'oscillations libres) qui est parfaitement décelable par l'oreille et qui mérite donc d'être appelée "transitoire de résonance".
Ce transitoire dure jusqu'à 2/10° de seconde; il peut être relativement audible.

3) le transitoire (de résonance) par filtrage des fréquences élevées qui ne sont pas des fréquences propres du résonateur que constitue la corde

4) le transitoire de résonance qui concerne les modes longitudinaux de la corde et qui est relatif à certaines non-linéarités que nous examinerons plus loin.

5) un autre transitoire de résonance qui concerne les modes transversaux de la corde et qui est relatif à certaines non-linéarités affectant le "précurseur" (voir également plus loin).

On a donc à la fois un transitoire d'excitation (propre au pincement) et quatre transitoires de résonance (spécifiques de la corde et indépendants, quant à leur existence, du mode d'excitation) qui viennent composer ce que l'on appelle communément "le (!) transitoire d'attaque" de la corde pincée. Il serait tout à fait restrictif de réserver au seul transitoire d'excitation le terme de transitoire, ne serait-ce que parce qu'il est toujours possible de percevoir un transitoire (au sens musical du terme) lors même qu'on a retiré au son sa tête, en l'occurrence la brève partie initiale qui correspond à la durée de l'excitation (temps de pincement).

Je m'établirai donc en cette distinction (transitoire d'excitation / transitoire de résonance), tentant de m'y tenir dans la suite de manière aussi rigoureuse que possible.

Je distinguerai alors 5 types de transitoire de résonance:
1) le transitoire (de résonance) tenant aux amortissements inégalement répartis selon les fréquences;

2) le transitoire (de résonance) de filtrage par résonateur

3) le transitoire (de résonance) longitudinal;
4) le transitoire (de résonance) affectant le "précurseur";
5) le transitoire (de résonance) relatif à la dualité "son immédiat / son rémanent" dans l'évolution des cordes du piano. Comme on le verra, c'est là un transitoire-limite en raison de l'importance exceptionnelle de sa durée mais en matière de transitoire - et en particulier de transitoire de résonance - tout est naturellement question d'échelle relative.
Le troisième et le quatrième transitoires (de résonance) supposent l'existence de non-linéarités (ce sont même très précisément les non-linéarités qui dans ces cas font le transitoire) alors que le premier, le deuxième et le cinquième ne les nécessitent nullement.

Non-linéarité.
Comme il est d'usage, on emploiera ce terme à propos des corrélations entre excitation (E) et réponse (R).
[ Si E=>R et E'=>R' la linéarité correspond à: p*E + q*E' => p*R + q*R' ]

Distinguer linéarité d'une équation de la non-linéarité de ses fonctions-solutions. Ici ex. de non-linéarité des amortissements selon la fréquence quoique les amortissements soient linéaires du point de l'excitation

On décèlera alors 4 situations de non-linéarités dans le cas de la corde:
1) le transitoire (de résonance) longitudinal est l'effet d'un couplage non-linéaire des modes longitudinaux avec les modes transversaux (cf. Cuesta et Valette).
2) la réponse transversale nommée "précurseur" est affectée de manière non-linéaire par les excitations transversales (cf. Cuesta et Valette).
3) le feutre du marteau a un fonctionnement non-linéaire en même temps que non-réversible (compression dilatation; cf. Boutillon):
Si la modification (en y) est fonction de la force (F) on a:

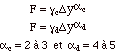
(c: compression, d: dilatation)
4) l'alternance adhérence/glissement dans les contacts archet-corde est affectée de non-linéarités (en même temps que d'hystérésis générant l'effet dit de "bémolisation"; cf. Schumacher).

Amortissements
Pour la corde à nu ils sont essentiellement dûs aux facteurs suivants:
* la viscosité de l'air (cause déterminante à basses fréquences)
* les frottements internes (causes prépondérantes à plus hautes fréquences) dûs à
- la propagation du point anguleux,
- la conduction de la chaleur entre parties comprimées et étirées,
- la mise en vibration des dislocations dans le métal.
De ces trois dernières causes, la première est fonction de la fréquence selon la loi suivante:

car Q(f)=f*Dt(f)
avec: Q(f) = coefficient de qualité, T = tension, f = fréquence, Y = module de Young, r = masse volumique, r = rayon et d = angle de pertes (cf. aussi p.75 de "Journées pédagogiques...")
Dt(f), temps de décroissance (à 10 dB) du partiel de fréquence f, est ainsi fonction très décroissante de f.
Dans MOSAIC, toutes choses égales par ailleurs, plus la corde est inharmonique (plus le "module de Young" est élevé), plus les amortissements (plus les "pertes" effectives) ont tendance à être prononcés. Ceci traduit une corrélation physique qui tient au fait que ce sont les mêmes causes (raideur de la corde...) qui engendrent à la fois l'inharmonicité de la corde et ses amortissements.
Il est d'usage de considérer les amortissements comme linéaires, ce qui se justifie aisément pour les petites oscillations.

D'autres équations d'amortissements? cf. Morge??

Pour la corde montée, s'ajoutent à ces différents amortissements ceux attribuables au chevalet et à la caisse/table d'harmonie.

Helmholtz % d'Alembert?
parallélogramme / parabole => remonter ici le parallélogramme...
importance ou non du point d'excitation de la corde dans le cas de la corde idéale?

Si on laisse une corde non idéale osciller librement après excitation, on constate un amortissement progressif qui tient aux données physiques rappelées précédemment. Ce phénomène, qui s'étend en vérité pendant toute la durée d'oscillation de la corde, connait cependant dans le temps même de la résonance plusieurs régimes qui tiennent à la diversité des causes d'amortissement.
Dans le cas qui nous occupe ici on peut constater un filtrage rapide de fréquences élevées qui tient semble-t-il à deux choses:
1) les amortissements affectent différemment les fréquences; en particulier les amortissements par frottements internes à la corde étant proportionnels à l'inverse du carré ou du cube de la fréquence, les hautes fréquences sont beaucoup plus rapidement affectées

TR par amortissement cf. "corde idéale amortie"

2) il y a auto-élimination des fréquences initiales n'appartenant pas au spectre des fréquences modales; un paquet "continu" de fréquences élevées, généré lors de l'excitation, se voit ainsi rapidement filtré et rabattu au spectre discret de la corde.
Au total ceci génère une évolution rapide du régime d'oscillations libres qui dans certaines conditions peut être isolé et entendu comme tel (cf. exemple sonore correspondant aux graphiques 12 à 15 pour lequel ce second facteur est décisif).

II TR par filtrage (à l'intérieur d'un résonateur) ou par absorption de fréquences

Cf. la corde est ici considérée comme un résonateur (en l'absence même d'une caisse ou d'une table d'harmonie)
cf. filtre en peigne????

cf. p.75 dans "Journées pédagogiques d'acoustique musicale": plus un partiel est rapidement amorti, plus sa largeur spectrale augmente et donc est difficilement repérable.Cf. durée d'extinction inversement proportionnelle à la largeur spectrale:

Deux modalités générales de transitoires de résonance - qui interviennent donc après que la corde est relâchée (cf. Cuesta et Valette) - sont l'effet singulier de non-linéarités et tiennent aux mécanismes suivants:

Présenter d'abord (?) leur généralité à partir des équations de Morge...
Cf. un point de la corde passe de x0=(x,0,0) à xt=(x+a,b,g)

1) La réponse longitudinale d'une corde pincée transversalement (en y/z) est dûe au couplage des modes longitudinaux d'avec les modes transversaux. Ceci vient de ce que la tension moyenne d'une corde mobile transversalement n'est pas constante (cf. le parallélogramme de d'Alembert) ce qui affecte en retour les évolutions longitudinales.

Il se trouve de plus que ce couplage n'est pas linéaire: Cf l'équation (1), linéaire en a, ne l'est pas en b (et g )

Dire quelle logique physique préside à cette non-linéarité: rayon de courbure???

Comme le coefficient d'amortissement longitudinal est important, l'effet du couplage se manifeste brièvement et génère ainsi un éphémère transitoire (de résonance).

(1 bis)

où Cl = célérité des ondes longitudinales et Ct = célérité des ondes transversales
avec Cl > Ct (de 35 à 1000 fois plus);
cf. Watzky:
et
avec Y = module d'Young, m = masse linéique, S = surface de la section droite et T = tension

(1 ter)

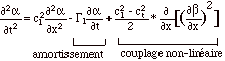
2) La réponse transversale nommée "précurseur" tient à l'inharmonicité de la corde: sa raideur génère une dispersion des partiels qui, progressant à vitesses ( ) différentes le long de la corde, ne se superposent plus en phase comme dans le cas de la corde idéale (parfaitement harmonique).
On constate, en plus de ce mécanisme, une non-linéarité qui rend ce précurseur peu décelable à faible pincement et très présent à fort pincement; elle tient au terme cubique de l'équation (2) qui tend d'autant plus à renforcer les hautes fréquences que l'amplitude du pincement initial (en y et/ou z) est importante.

Dire à quoi tient cette non-linéarité d'un point de vue physique.
Cf. Morge: développement limité
Mais Watsky semble le présenter comme
1 effet de la raideur => atténuation des modes élevés!
2 couplage dû aux non-linéarités géométriques
Noter que Watsky rajoute son 5° terme comme effet cette fois des modes en torsion de la corde! (cf. une corde montée tordue sonne souvent plus juste).

Cet effet est d'ailleurs d'autant plus prégnant que l'amortissement linéaire est faible pour les évolutions transversales.
Cette non-linéarité tend donc à diversifier le précurseur selon le mode d'attaque. Elle tend également à le profiler au cours du temps puisque la non-linéarité (cubique) en x équivaut à une non-linéarité en t; cf.:

Par là cette non-linéarité institue un transitoire (de résonance) transversal qui est a priori moins bref que le précédent (longitudinal).

(2 bis)

hypothèse du passage à cette nouvelle équation (outre l'amortissement introduit):
on prend un mouvement initialement plan (en x et y) et, comme il n'y a pas de modes en torsion, on n'a pas de couplage entre les deux dimensions transversales. On néglige le terme longitudinal (est-ce bien justifié????)

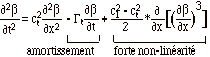
Un transitoire (de résonance) afférent au piano se manifeste par une double décroissance du son qui permet de distinguer le régime "immédiat" du régime "rémanent". Le terme "transitoire" fonctionne ici en son sens musical le plus large puisqu'il caractérise la transition entre premier et second régimes (le premier dure de 2 à 3 secondes). Ce transitoire (de résonance) procure le "moelleux" du son de piano plutôt qu'il n'opère pour son identification. Physiquement cette dualité - qui n'implique pas à elle seule de non-linéarités - tient à deux choses:

1) l'existence de deux polarisations de la vibration (en y et z): la polarisation en y est due aux irrégularités du marteau et de la corde. Ces deux orientations ne s'amortissent pas de la même façon au niveau du chevalet et surtout de la table d'harmonie: le son "immédiat" tient à la prédominance des vibrations en z (initialement 10 fois plus importantes mais très fortement amorties) et le son "rémanent" à celle des vibrations en y (moins fortes initialement mais également moins amorties par le chevalet et la table). Cet effet existe donc pour une simple corde montée sur chevalet, sans qu'un couplage avec d'autres cordes soit ici nécessaire (Cf. cas des cordes graves du piano). Il y faut cependant un chevalet de piano, sensiblement différent d'un chevalet de violon ou violoncelle en ce qu'il dissymétrise très fortement les amortissements en y et en z.

2) le couplage des cordes (par 2 ou par 3) déforme cette dualité en fonction des relations de phase ou de fréquences entretenus par les différentes cordes. Un très petit déphasage initial et un léger écart par rapport à l'unisson (<1/1000°) vont générer un amortissement plus prononcé au niveau du chevalet (donc en cours de "régime immédiat") en même temps qu'ils vont tendre à s'annuler par phénomène de transfert et de compensation (à ce même niveau du chevalet). L'unisson et la mise en phase ainsi engendrés conduisent alors à un nouveau régime ("mode presque symétrique"), notablement moins amorti que le précédent ("mode presque anti-symétrique"), qui va accuser le caractère alors prédominant du son c'est-à-dire précisément lors du "régime rémanent". Le couplage - s'il est correctement réglé - majore ainsi les contrastes entre les deux régimes immédiat/rémanent.

1) Linéarité/non-linéarité: le logiciel est construit sur une contrainte générale de linéarité des objets (hypothèse canonique en matière de représentation modale). Par contre le logiciel simule bien sûr la non-linéarité des connexions (entre objets), non-linéarité relative aux discontinuités entre les régimes de contact et de non-contact. Ainsi - cas extrême - l'interaction frottée (avec archet) est une commutation incessante (tous les 1/100° de seconde au moins) entre 7 régimes différents de rapports crin-corde: 6 pour le glissement (où la corrélation non-linéaire entre force d'interaction et vitesse relative corde-archet est approximée par 6 régimes linéaires différents) et un pour l'adhérence.

Attention cependant à mieux distinguer:
pseudo non-linéarité par discontinuité: ici par rupture de régimes dans la connexion archet-corde qui se fait ou ne se fait pas, qui passe d'adhérence à glissé...
non-linéarité stricte d'une même fonction: ici à l'intérieur même de la connexion glissée archet-corde car les 6 segements ne sont qu'une approximation linéaire d'une hyperbole (non-linéaire!)
Il ne faut donc pas compter 7 (6+1) mais deux statuts différents.

2) Bi-dimensionnalité: la représentation physique retenue pour la corde se fait selon deux dimensions (transversales) et non pas trois (modes longitudinaux) - ou même quatre (modes en torsion) -. On n'a donc pas de modes longitudinaux quoiqu'il serait possible de compléter le logiciel sur ce plan (cf. équivalence de principe des modes longitudinaux d'avec les modes d'un tube ouvert-ouvert). Ceci ne touche pas à une limitation intrinsèque de MOSAIC mais seulement à l'état de la bibliothèque des objets déjà analysée et donc actuellement disponibles.
Mentionner ce point n'infère nullement qu'il soit prioritaire de développer la bibliothèque sur ce plan: le choix d'une corde bi-dimensionnelle comme principale étape de la formalisation s'est avéré judicieux puisque comme on le verra les principaux transitoires de la corde (ceux qui ont une efficacité musicale plus encore qu'acoustique) tiennent avant tout aux deux dimensions transversales privilégiées.

3) Non-couplage/couplage: les deux dimensions transversales retenues pour la corde ne sont pas couplées et les modes, d'une dimension à l'autre, sont donc indépendants (matrice diagonale par blocs).
Il faut ajouter que MOSAIC simule cependant deux modalités d'interactions entre évolutions transversales:
* au niveau du chevalet: les deux modes élastiques (qui correspondent à une déformation générale du chevalet) et le mode inélastique de rotation par bloc conjoignent des évolutions en y et z;
* au niveau du jeu d'archet: la force-limite (en y) à laquelle la corde décroche du crin est fonction de la pression exercée verticalement (en z) par l'archet:
avec Dm (Delta mu) fonction de la colophane (cf. graphiques 33 et 34)
puisqu'on a en général où vr est la vitesse relative corde-archet (cf. Lazarus).
Ainsi le non-couplage au niveau de la corde s'accompagne d'un couplage par les extrémités (le chevalet).et par l'archet.

* MOSAIC simule tous les transitoires d'excitation. La totalité des transitoires (d'excitation) de la corde bi-dimensionnelle (pincée, frappée, frottée) apparaissent d'ailleurs musicalement pertinents; ce sont:
- les transitoires d'attaque (par marteau ou plectre) qui se projettent en "ombre portée" sur la résonance;
- les transitoires d'extinction: étouffoir...;
- les transitoires afférents aux répétitions d'attaques mais aussi d'entretiens: cf. les transitoires relatifs aux alternances tiré-poussé, aux notes-legato...

* MOSAIC simule également le "précurseur", quoiqu'avec quelques difficultés de calculs tenant au nombre important de modes à prendre en compte (cf. graphiques 5 à 8): en effet dans le cas de cordes faiblement inharmoniques (cf 3) l'existence du précurseur repose sur la faible convergence de la série harmonique qui conduit la somme de nombreux éléments infinitésimaux (cf. 4) à ne plus être négligeable.

(3) Inharmonicité:
avec:

(4) Force résultante:

* MOSAIC méconnait par contre la non-linéarité du précurseur et donc le transitoire de résonance qu'elle engendre. On peut cependant construire (grâce aux options d'hybridation incluses dans MOSAIC) quelque artifice pour simuler une telle non-linéarité et ainsi générer le transitoire (de résonance) afférent. Il apparaît alors que l'efficacité auditive d'un tel transitoire (de résonance) soit relative à des conditions d'inharmonicité et d'amortissements assez circonscrites.

* Même chose pour la non-linéarité et l'hystérésis du feutre du marteau: on peut par hybridation générer ces phénomènes en sorte d'adoucir le contact marteau-corde et raboter les hautes fréquences inhérentes aux claquements trop prononcés. Il apparait cependant que l'effet auditif d'une telle opération tienne avant tout au contexte instrumental de la corde: comme on le verra plus généralement, les effets percussifs sont peu audibles dans le cas d'une simple corde à nu et ne s'entendent qu'en situation de montage de la corde: par mise en vibrations des autres pièces du piano.

* MOSAIC, en l'état des bibliothèques disponibles, ne simule pas la réponse longitudinale et méconnait donc a fortiori sa non-linéarité, agent du transitoire (de résonance) longitudinal.

* MOSAIC reproduit les différences de polarisations en y et z dans le cas de la corde simple et permettrait donc d'obtenir la distinction entre "son immédiat" et "son rémanent" propre aux cordes montées du piano; le problème reste celui de la bibliothèque: les seuls chevalets actuellement disponibles (violon et violoncelle) dissymétrisent trop faiblement les deux évolutions transversales (en y / en z) que le chevalet du piano différencie plus nettement.
MOSAIC simule le déphasage et le léger écart d'unisson entre deux cordes jumelées et saurait donc reproduire correctement l'effet du jumelage de plusieurs cordes sur le piano (via le chevalet et la table d'harmonie) sous les conditions précédentes (bibliothèque à compléter).
MOSAIC saurait également engendrer l'effet de la pédale una corda (plus grande prégnance de la partie "rémanente" pour les sons faibles, d'où une sonorité adoucie et durable) et la suggestion faite par Weinreich d'une pédale spéciale créant une accentuation ("reconversion") en cours de vibration (par "étouffoir fendu") serait testable dans le cadre de ce logiciel.

* MOSAIC simule le transitoire (d'excitation) qui précède le régime pseudo-périodique de l'archet et qui tient pour l'essentiel au fait que la pression verticale (en z) oscille quelque temps après le contact avant de se stabiliser (ce qui génère des irrégularités dans le régime adhérence-glissé en y).
Noter que ce transitoire (d'excitation) dure sensiblement plus longtemps que les autres transitoires (d'excitation) afférents aux attaques: 1/10° de seconde contre un 1/50° pour le plectre et seulement quelques millièmes de seconde pour le marteau.

Au total, il apparait que les transitoires que l'on perçoit - a minima comme "quelque chose" à défaut de pouvoir nécessairement les isoler et les discerner les uns des autres - sont:
- les transitoires classiques d'excitation: cf. attaque (+ son "ombre") pincée, frappée, frottée; cf. extinction par étouffement; cf. répétitions diverses...
- les transitoires (de résonance) relatifs aux amortissements.
Ainsi la part la plus significative (d'un point de vue auditif) des transitoires de corde est absolument compatible avec une modélisation strictement linéaire ce qui explique qu'ils soient tous intégrés dans MOSAIC. Ceci valide rétrospectivement les choix opérés quant à la linéarité du logiciel.
On peut alors remarquer les points suivants:
1) la perception d'un frappement de la corde (par un marteau) n'est discernable d'un pincement qu'en situation de corde montée: l'effet percussif semble ainsi tenir au contexte instrumental de la corde (cf. la lutherie et ses autres objets mis en branle par le choc du marteau) plus qu'à la corde elle-même.
2) la perception du pincement comme tel semble impliquer un certain temps minimum de contact plectre-corde (de l'ordre d'1/30° de seconde) permettant à la corde d'entrer en vibration sous le seul effet de ce choc. A contrario la trop grande brièveté du contact marteau-corde est ce qui paraît interdire de le percevoir en dehors d'un contexte instrumental approprié.
Il apparait plus en général que les configurations en matière de lutherie (diverses situations de montage pour les cordes) joue un rôle capital tant pour le repérage des transitoires que de manière plus générale; ainsi la perception de l'inharmonicité d'une corde semble fortement majorée par sa disposition instrumentale.

Cf. dossier graphique et exemples sonores présentés en séance.

A) Développements

* Physique appliquée: développement de la bibliothèque d'objets disponibles par analyse modale. La liste se présenterait a priori ainsi:
1. chevalets, tables d'harmonie/caisses: faire l'analyse modale de ces objets pour d'autres instruments (piano, alto...)
2. analyse plus systématique (quoique propre à chaque objet!) des interactions entre types de modes;
3. cordes: analyse modale tri- et quadri-dimensionnelle par adjonction des modes longitudinaux et des modes en torsion (significatifs dans l'interaction frottée)
4. analyse des interactions pincée, frappée et frottée en trois ou quatre dimensions
5. chevalets: compléter l'analyse modale des chevalets existants. Il y a théoriquement six dimensions élastiques pour un chevalet; le logiciel en simule actuellement quatre: deux dimensions élastiques (mode "sandwich" et mode "papillon", actifs à la fois en y et en z) et deux inélastiques (translation par bloc en z et rotation en bloc dans le plan y-z)
Cette liste n'est nullement prescriptive: le premier point est important; le deuxième peut avoir un coût très/trop élevé; les troisième, quatrième et cinquième points ne sont pas prioritaires, surtout relativement au travail à mener en matière de rayonnement!

* développement informatique: implémentations d'hybrides d'hybrides (dans la modalité glissé-glissé) pour arriver à opérer sur des hybrides (glissés) à deux dimensions et plus; l'hybride "glissé" garde en mémoire les évolutions passées de l'objet hybridé là où l'hybride "fondu" ne réalise qu'une interpolation instantanée. Ceci renforce l'intérêt de l'hybride "glissé" et ce d'autant plus qu'on se rappellera que la puissance spécifique des hybrides de MOSAIC est de pouvoir être excités.
Cependant comme on dispose déjà de certains hybrides à deux dimensions (fondu-glissé et glissé-fondu), peut-être faudrait-il au préalable réfléchir à une reformalisation générale de la question des hybrides (cf. remarques de Jean-Marie dans "Notes sur l'interface de contrôle").

* applications en l'état du logiciel:
1. hybridations diverses en cours qui introduisent diverses modulations (amplitude, fréquence...) au coeur du fonctionnement modal et qui génèrent des non-linéarités par rebouclage des éléments de MOSAIC les uns sur les autres.
2. sans attendre de disposer d'un chevalet et d'une table d'harmonie de piano, on pourrait, avec les objets existants de MOSAIC, construire des ersatz permettant d'expérimenter les différents effets de cordes jumelées, le jeu de la pédale douce et la proposition d'étouffoir fendu de Weinreich.

B) Implémentations de non-linéarités
Il s'agirait là d'un développement physique plus "théorique": implémentation d'équations non-linéaires pour diversifier les connexions entre modes. Il importe de garder présent à l'esprit le coût en termes de modularité et de temps de calcul de telles implémentations: la difficulté tient à la diversité des situations particulières rencontrées qui peut conduire à chaque fois à des solutions distinctes et non transposables quoique restant très lourdes en temps de recherche et de calcul. C'est d'ailleurs ce qui justifie que ce type d'implémentations n'ait pas été jugée prioritaire.

C) Recherche de fonctionnements chaotiques imposables aux évolutions physiques.
Le but musical serait d'inventer de nouveaux régimes de fonctionnement des cordes qui soient pseudo- ou a-périodiques et qui puissent ainsi diversifier la résonance des cordes (après excitation):
* régimes pseudo-périodiques: cela revient à travailler le spectre résonant dans une logique inharmonique et discrète.
* régimes apériodiques: cela donnerait accès à un travail temporel d'un spectre continu. Cf. intérêt ici des modèles physiques pour travailler un tel spectre (qui pourrait être, dans le cas du chaos, un bruit très coloré en raison de l'existence générale de "points périodiques" dans les systèmes dynamiques chaotiques): on opère là sur une cause, non sur le spectre résultant.
L'intérêt du chaos (par rapport au pseudo-hasard qu'est l'aléatoire probabiliste- cf. le piètre "random") tient me semble-t-il au fait que le chaos est un ordre sans périodicité. Le chaos introduit ainsi une corrélation entre instants qui, quoique déterministe, n'est pas prévisible; dans notre cas, ce serait le système physique qui serait alors en charge de la "mémoire" des évolutions passées.
On pourrait par exemple travailler la réponse pseudo-périodique d'une corde (inharmonique) en suivant le "modèle" du jeu d'archet (alternances adhérence-glissé) pour inventer une modalité d'intermittence entre deux régimes (par oscillation entre deux "attracteurs" ordinaires). On pourrait également engendrer un entretien apériodique sous l'effet d'"attracteurs étranges" (cf. les équations différentielles chaotiques disponibles). Cela supposerait sans doute d'avoir au préalable résolu le problème mentionné plus haut d'hybrides-glissé à plus d'une dimension.
Au total l'idée serait d'inventer (par hybridation dynamique) des nouveaux régimes d'entretien qu'on pourrait nommer (paradoxalement!) "résonances chaotiques".

D) Développement de l'aspect psycho-acoustique.
Un des intérêts de MOSAIC est de permettre d'isoler très précisément un phénomène physique dont on souhaiterait tester l'efficace perceptif.
La prolongation de ce travail pourrait intéresser peut-être un psycho-acousticien.

*

Cet ensemble de perspectives disparates suggère qu'il y a en fait trois orientations de travail qu'il convient je crois de mener en parallèle:
1) multiplier ce qui a déjà été réalisé dans un cas particulier: par exemple refaire pour l'alto ou le piano ce qui a déjà été fait pour le violon ou le violoncelle (chevalet...).
2) approfondir localement un modèle instrumental déjà existant en progressant dans l'approximation de la réalité par la puissance de calcul: par exemple mieux reproduire tel chevalet ou telle corde...
3) inventer de nouveaux fonctionnements instrumentaux: par exemple des excitations hybridées et autres "résonances chaotiques"...
On voit que le premier axe consiste à travailler horizontalement (selon l'étendue), le second verticalement (selon la profondeur), le troisième obliquement ("déclinaison" du logiciel). Le premier relève de la physique appliquée, le deuxième de la physique plus théorique, le troisième relève d'un travail plus musical.
On est là, il me semble, au coeur de l'esprit de MOSAIC: il s'agit à la fois de fournir une bibliothèque la plus diversifiée possible d'instruments traditionnels (premier axe); il s'agit en même temps d'améliorer la qualité de chacun de ces instruments en sorte de modéliser tant qu'à faire un bon violon plutôt qu'un médiocre (deuxième axe); et cependant on ne saurait se satisfaire de reproduire informatiquement ce que la nature et la culture musicale traditionnelle feront toujours beaucoup mieux que l'ordinateur (troisième axe où l'on fait un usage biaisé des deux premiers). La première orientation de travail est finie car la liste d'instruments musicaux est fini. La deuxième est une tâche infinie car chaque instrument est lui-même infini ("les objets contiennent l'infini" disait un poète). La troisième l'est également, mais d'une tout autre manière: non plus l'infini potentiel d'un parcours sans fin mais l'infini actuel de ce qui peut venir au jour comme nouvel instrument.
Il sera clair, je l'espère, que s'agissant des transitoires de corde, je suggérerai plutôt le fini et l'infini actuel que l'infini potentiel; plus prosaïquement les perspectives qui me semblent à retenir sont celles de prolifération (des objets, instruments et régimes représentés...) et d'invention (de nouveaux régimes...) plutôt que celle d'approfondissement (chevalet à 6 dimensions, cordes à 4 dimensions...)

Je ne mentionne ici que des travaux et publications extérieurs à la problématique des modèles physiques, la référence aux travaux de J.M.Adrien, O.Calvet, S.Champeaux, (I.Chayé: pas modèles physiques!) ... allant sans dire pour qui travaille avec MOSAIC.

* Couplage longitudinal/transversal
Morge et Ingard:
Cuesta et Valette:
- "Le transitoire d'attaque des cordes de clavecin"
- "Evolution temporelle de la vibration des cordes de clavecin"
- "Transitoire d'attaque des cordes pincées ou frappées; phénomènes non linéaires"

* Non-linéarité du feutre du marteau: X.Boutillon
- "Le fonctionnement des instruments à corde libres: approche mécanique - traitement du signal"

* Jumelage des cordes du piano: G.Weinreich
- "Coupled piano strings"
- "Comment vibrent les cordes jumelées d'un piano"

* Hystérésis du jeu d'archet: Shumacher
- "Self-sustained oscillations of the bowed string

* Perception du transitoire-legato: Campbell et Heller
- "The contribution of the legato transient to instrument identification"

Citer A.Watzky: "Vibrations libres des cordes en régime non-linéaire"

Sauf contre-indications:
* on dispose le temps en abscisse et en ordonnée la position du point de la corde où porte l'excitation;
* le taux d'échantillonnage est toujours 32000.

Corde (quasi-)idéale à nu:
1: pincée: l'excitation lente
2: juste après l'excitation
3: une seconde plus tard
4: oscillations en différents points

montrer effets différents selon le point pincé:
au milieu => créneau symétrique;
en bout => +- impulsion (cf. plus d'aigus) si l'on regarde au chevalet donc vers le résonateur

Précurseur sur une corde très inharmonique (module de Young = 10 puissance 10):
5: 20 modes
6: 40 modes (attention: changement d'échelle verticale)
7: 80 modes
8: 150 modes

9: juste après l'excitation
10: 1/3 de seconde plus tard
11: 2/3 de seconde plus tard

Transitoire (de résonance) par amortissements (cf. expérience)
12: excitation
13: début du régime d'oscillations libres
14: 2/10° de seconde plus tard
15: une seconde plus tard

Corde pincée:
(on ajoute dans les graphiques la position de la corde en un endroit éloigné du point d'excitation ainsi que la position de l'extrémité du plectre)
16: plectre dur (corde à nu)
17: plectre mou (corde à nu)
18: plectre mou, corde montée sur violoncelle (chevalet + caisse)
19: répétitions (plectre dur, corde à nu)

Corde frappée
(on représente à la fois la position de la corde et la force exercée sur le feutre du marteau)
corde à nu:
20: position
21: force
corde montée sur chevalet:
22: position
23: force
cas singuliers:
24: corde à nu frappée en z et y: positions
25: deux cordes jumelées (légèrement désaccordées) frappées presque simultanément: positions
26: répétitions (sur une corde à nu)

inclure corde frappée sur une surface et non plus en un point: plotter différentes positions sur la corde

Corde étouffée:
(on ajoute dans les graphiques la position du bout du plectre)
27: étouffoir par plectre dur
28: id. avec zoom sur le transitoire
29: id. la corde étant ici montée sur violoncelle
30: étouffoir par plectre très mou

Corde frottée:
30 position en z pendant le transitoire d'attaque
31: force en z pendant le transitoire d'attaque
32: vitesses et force en y pendant l'entretien pseudo-périodique
33: vitesses et force en y pendant le transitoire d'attaque
34: force en z pendant le transitoire d'attaque(zoom de 31)

35: répétitions: tiré-poussé

Rajouter
* TR par amortissements
- corde idéale non amortie
- corde idéale amortie
* TR par filtrage
- corde idéale avec sinus => filtrage?
* Combinaison des eux: cf. 12 à 15

Mettre force en y sur l'archet et pas la corde dans 33

corde frottée montée sur chevalet + caisse