The
Hexagon of Opposition in Music
François NICOLAS
(Ens-Cirphles)
(Translation by Liam Flenady)
Abstract
In what ways can the hexagon
of opposition formalise what the musician calls “musical logic” and by doing so
aid him in better understanding what “negation” and “deduction” mean for the
music at work?
To respond to this question,
this presentation will propose successively three ways of appropriating this
hexagon for musical realities: the first – briefly outlined – will depart from
the diatonic/chromatic opposition; the next – sketched with more detail – will
touch upon the rhythm/timbre opposition. Finally, the third – largely developed
– will undertake to formalise properly musical discursivity by orienting it
according to three principles. These in turn will be counterposed term by term
to the great logical principles of Aristotle: a principle of ambiguity (as opposed to the
principle of identity), a principle of constrained negation (as opposed to the
principle of non-contradiction) and a principle of the required middle (as opposed to the
excluded middle).
These three principles
configure the musical composition as an interaction between three
“entities” (an initial entity, its alteration and an entity of another
type), an interaction that this presentation will undertake to formalise
in the form of a hexagon of opposition. The detailed interpretation of this
will suggest in return that the development of musical discourse (that which
takes the place of musical “deduction”) operates as a Borromean knotting of
three forms of alteration (musically taking the place of “negation”).
*
I would like to reflect with you upon different ways of appropriating
the hexagon of opposition for musical questions.
What are the musical oppositions that this hexagonal formalisation is
capable of theorising and what in way can this kind of formalisation clarify a
musical model in return?
I will make use here of the
terms model and theory in the mathematical understanding that they have in
the “theory of models”: the model here is the original that it is a matter of
copying, the “canonical” model; the theory is that which formalises this model
and in return gives rise to interpretations in the initial model.
The words are thus employed
here in their original sense, which a neo-positivist trend has unfortunately
reversed (where “model” then designates “the reduced model,” or “the scale
model”).
In itself, music does not thematise what musical opposition means. Music
presents itself in notes and in sounds, at a distance from all speech. The
words “opposition” or “negation” do not take part in its repertoire, and the
score does not know the signs “→” and “=/≠”.
The score simply mobilises the identity and difference of the signs of
solfege: a musical sign will differ from another, either by its form (# and ♪),
or by its place.
Thus music mobilises its own principle of differentiation in order to
play with resemblances and dissemblances, similitudes and differences.
In the vocabulary of Alain
Badiou (Logics of Worlds), we will say that music has its own transcendental
that constitutes it as an autonomous world. This transcendental is solfege and
the nominal categories of opposition do not belong to solfege…
In no way is all difference a matter of “opposition”: two musical
objects (apprehended by writing or by the ear) could be different without for
all that being opposed. Opposition is a particular relation, whereas difference
remains a static relation that emerges as an exterior rapprochement rather than
an endogenous process. Opposition is a dynamic and endogenous relation.
Difference is a static and exogenous relation.
In other words, in order to identify the play of musical oppositions, it
is necessary to have something other than the score alone; it is necessary to
bring to the scene the musician, the one who executes and interprets the score:
it is he in fact who will be able to declare and above all to effectuate (by
playing!) the reality that such objective musical difference is a matter of
opposition or not, and possibly negation.
It is the musicianly
interpretation that gives a logic to the score, that renders it effective, that
is to say sensible.
Thus I will here outline, as a musician, how to my eyes – and above all
to my ears! – music puts to work oppositions, and how these oppositions can be
formalised according to a logical hexagon that gathers us together here.
In order to do this, I will propose to you three attempts to appropriate
our hexagon of musical oppositions in play.
· The first is an
attempt that will prove to be abortive since is will not be possible to
stabilise for it a genuinely musical sense.
· The second will
bear upon the local organisation of material: it will be structured by the
opposition of rhythm and timbre.
· The third will bear
upon the global development of musical discourse: it will pivot around the
great opposition between variation and invariance.
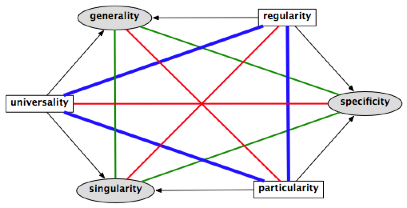
1. A hexagon
opposing tonal/atonal, major/minor, diatonic/chromatic
Let is depart from two contradictories tonal/atonal (a musical opus
partakes of one or the other, if we understand by “atonal” that which is not
tonal and not uniquely that which was inscribed under this name between 1909
and 1923: let us say that “tonal” operates here as a common name, not as a
proper name).
The tonal could be seen as the sum of major and minor, which constitute
its contraries. The atonal, for its part, is the product of the subcontraries diatonicism and chromaticism, which thus
complete the hexagon:
![]() ⇒
⇒  ⇒
⇒ 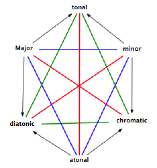
The hexagon thus produced remains however unsatisfactory for at least
three reasons:
· the contradictions major-chromatic
and minor-diatonic are not musically equivalent to the first contradiction
tonal/atonal: the latter is strong, the formers are weak…
· the subcontraries
of the triangle diatonicism-chromaticism-tonality are forced: if one can
maintain that a musical proposition can not be at the same time neither
diatonic, nor chromatic, it is more difficult to maintain that it would not be
able to be at the same time neither diatonic, nor tonal.
· it lacks, in this
formalisation, a usual term that would form a contrary or subcontrary
(depending on the way in which one understands this musically) with tonal, and that is the
term modal.
In sum, one gets the sense of forcing the musical proposition in order
to arrive at inscribing it in an inadequate formal framework.
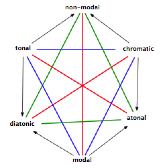
Then, a better hexagon will be this one, which leaves the contrary of
major and minor in order to introduce the contradiction of modal and non-modal.
We can see that the opposition diatonic-chromatic is now, more logically, a
contradiction (and no more a sub-contrary!), that the tonal is now the product
of diatonic and non-modal (and no longer the sum of major and minor) and – last
but not least- that our hexagonal figure is now well-structured by the triangle
of contraries {modal, tonal, chromatic}.
But let us leave this first attempt and examine another way of musically
approaching the hexagonal formation.
2. The Hexagon
of Rhythm and Timbre
Let us depart this time from the classical contradiction between rhythm
and timbre, a contradiction that we could configure equally as that of the
melody and the chord: the melody is horizontal and materialises a rhythm
(understood as a diachronic series of durations); the chord is vertical and
materialises a timbre (understood as synchronic series of intervals).
Each of these terms – melody as much as chord – will give rise to two
complementary forms: on one side, the rhythm of the melody gives rise either to
a harmonic rhythm of successive chords, or to a polyphonic rhythm of superposed
voices; on the other side, the timbre of the chord gives rise either to a
harmony understood as a suite of chords, or to a counterpoint understood as a
superposition (as “formants”) of voices.
If one divides this out amongst the six summits of the hexagon (disposed
here horizontally rather than, as is customary, vertically),[1]
we obtain the following hexagonal formalisation:
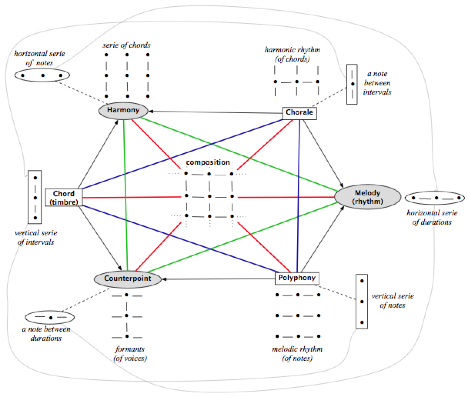
This formalisation sets in relief two new classical contradictions, on
the one side, that of the chorale and counterpoint, and on the other side that
of harmony and polyphony.
This hexagon can be divided into two trinities: that of the contraries
(the chorale, polyphony and the timbre-chord) and that of the subcontraries
(harmony, counterpoint and the rhythm-melody).
We see how the six summits “converge” upon a central object that figures
here as an integral musical meshwork.
In sum, this formalisation is internally stable: the figuration proposed
for each of the terms by way of points and dashes attests to its formal
pertinence. We will consider it thus as musically acceptable.
It has, however, one defect that is musically unacceptable: this
formalisation is essentially descriptive of the musical oppositions that are
inscribed here. It remains static insofar as it teaches us nothing more than
what we already knew (precisely what we needed to know in order to construct
the hexagon).
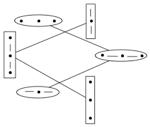
A remark
However, we will remark that this formalisation suggests a refolding
since certain objects, which were presented above without them belonging stricto
sensu to our hexagon, prove to be reliable by connections (drawn above in
thin lines) that we summarise here in the following schema:
Thus this would suggest another hexagonal disposition that would better
take account of the relations of implication (those of the periphery), but less
well of the transversal relations (those of opposition):
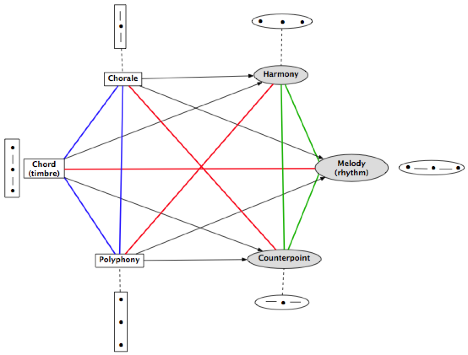
Here we come to a point that, in this type of formalisation, proves to
be difficult for us musicians: it conjoins a formalisation of oppositions (by
unoriented lines: contradictions in red, contraries in blue, subcontraries in
green) and a formalisation of implications (by lines oriented in black).
We find in our example the properly logical difficulty that is our own:
it does not go without saying that, musically, a musical regime of consequences
(arrows in black) and a musical regime of oppositions (lines in colour) are
strictly correlated.
· The musical regime
of consequences mobilises in general the figure of the chronological
(the before and after, that which precedes and that which follows) but in an
extremely open manner: it is not because B musically follows A that A→B (that
is to say, that B develops A); and inversely, it is not because B develops A
that B necessarily precedes A.
· For its part, the
musical regime of oppositions mobilises the very difficult question of the
negation in music: what is it that could give a musical value to negation,
knowing that the logical sign of negation does not exist in music, that all
music, by definition, poses an existence, affirms a presence (in music, even
silence is an affirmation: musical silence is not the negation of all sound; it
is the affirmation of a musical duration like any other, written and thus
counted as itself, not as zero 0 or the void set ø). Thus no music is able to
negate without affirming a negative. We could say that in this sense music
ignores the double negation since it cannot negate, as part of its very
constitution, a negative: music can affirm a negative (a contrasting
object, a different or altered one) or not affirm a positive (not
develop, not repeat, not alter an object presented) but it is not able to
effectuate a double negation.
Hence the interest for us in turning finally to a third hexagonal
formalisation more forward looking and in the end more instructive for us
musicians, a formalisation that will depart this time from the question: what
is the negation in music? Or better: what does it mean to musically negate?
3. The Hexagon of musical discourse
For this we will take up again what the question of what musical
discourse means.
Preliminary
remark
Logic is realised in music in three ways – or rather: there are three
understandings of what “musical logic” means.
· First of all there
is the logic of writing. This touches upon this dimension of logic that Alain
Badiou calls “transcendental”: music is endowed with a solfege – that is to
say, a proper mode of writing – which is what takes a properly musical measure
of sonic existences. I will not attempt today to formalise this fundamental
dimension of musical logic (in my jargon I call it “the scriptural logic of the
Music-world”) according to our principle, the hexagon of opposition.
· Then there is “the
discursive logic of the opus of music.” It is this that we will now explore in
more detail in order to attempt to formalise it according to our hexagon.
· There is finally
“the strategic logic of the musical work,” which concerns the compositional
project proper to a given work (a project taking up the projects of other works
already in existence, responding to them, or contradicting them, etc.). Each
musical work has for its real interlocutors other musical works (much more so
than musicians or auditors). This strategic (or subjective) dimension musically
at work will not be approached here.
Unsurprisingly: each of these three musical “logics” – more precisely
each of these three understandings of what “logic” wants to mean in music –
requires difficult operations of untangling with the question (itself already
quite tangled) of the negation: if negation can be said in general in at least
three ways (classical, intuitionist, paraconsistent) and if musical logic takes
form specifically in three ways (solfege, discursivity and intension at work), then it would be
necessary for us to examine at least nine possibilities![2]
Here I will content myself with clarifying the properly discursive
aspect of musical logic by way of the hexagonal formation.
The three
logical principles of musical discourse
We could introduce the logic of musical discourse by taking up the three
great logical principles of Aristotle, in order to counterpose to them three
musical principles according to what we could call a global antisymmetry between musical
logic and classical Aristotelian logic.
Identity versus differentiation
Whereas “classical” logic prescribes the principle of identity (A, stated twice,
is identical to itself in its different occurrences: A = A), the principle of
musical logic, that we could call the principle of differentiation, states that each
musical term stated twice bears, by that very fact, an alterity A≠A(’). Or: no term,
stated twice, is identical to itself. Or further still: in music, to repeat is,
ipso facto, to alter.
Non-contradiction
versus constrained negation
Where “classical” logic prescribes the principle of non-contradiction (I cannot state at
one and the same time A and non-A except to spill over into inconsistency Non(A
and non-A), music counterposes a principle of constrained
negation: each musical object posed must compose itself with itself
contrary, that is to say must compose itself by becoming, A (A and non-A) [3]. This is the way
in which musical discourse will appear for us as a paraconsistent logic.
Excluded
middle versus required middle
Where “classical” logic prescribes the principle of the excluded
middle (between A and non-A a choice is necessitated since there is no third
position: A or non-A), the musical composition poses a principle
of the required middle: each musical term posed should be composed with another term
that is other than the negation proceeding from the first, a neutral term (neutrum) since it is
“neither one nor the other,” A
(A and B). This is the way by which musical discourse
will appear for us as an intuitionist logic.
Com-position
In each of these senses to compose a musical discourse, this is to pose
together (com-pose) three terms: an initial musical term, its alteration and another
term, {A, A’, B}.
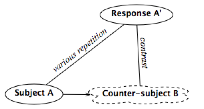
Example
of the fugue
We can remark that this principle of composition delivers the initial
matrix of all fugues: each fugue commences by posing a theme A (called subject), in order to
immediately set in train a varied repetition A’ (called response), which is
associated contrapuntally to a new object B (called counter-subject) that prolongs and
contrasts with the subject A.
See here for example the beginning of the Art of the Fugue (Johann-Sebastien
Bach), played on the organ by Wolfgang Rübsam (Naxos).

The response (A’) varies the theme-subject (A) in four ways
simultaneously:
· by repeating it
(thus by displacing it in time: on hearing it again, the thing is by this very
fact heard differently: no longer as initial presentation but as reprise),
· by displacing it to
another voice in the polyphony (here from alto to soprano),
· by transposing it
to the dominant (for reasons of harmonic differentiation),
· and finally by
subjecting it to some slight modifications (that we could call “mutations”) so
as to adjust the initial ambitus (a fifth I-V) to a new ambitus (a fourth V-I).
Formalisation
Formalising
the relations rather than the objects…
In order to formalise such a musical development in the framework of our
hexagon, it is necessary for us to operate at the level of the musical relations
between objects rather than directly between the objects concerned:
contradiction, contrary and subcontrary will need to be situated not between
the musical objects (our themes, motifs, harmonies, voices, rhythms…) but
between the musical relations that they sustain.
Thus one could not speak
properly of the subject and the counter-subject as contradictions, contraries
and subcontraries, but one could by contrast maintain that the relation of
varied repetition between subject and response opposes itself to the contrast
between response and counter-subject, etc.
Yet, as we will see very soon, this passage from musical objects to
morphisms that link them forces us to take leave of the strictly musical
terrain of the score for that of the musician who reads and interprets this
score. In fact it is indeed necessary to see that musical relations between
objects are not presented as such in the score: they are certainly present here
but they are in no way presented, and less still represented.
If I take for example our
fugue, the soprano voice presents me indeed with an alteration of the theme
initially presented by the alto but nothing in the score tells me that it is a
matter of an altered repetition. Of course, no musician will ignore this status
as altered repetition, and as a consequence all will phrase the two entries
according to the same principle of articulation. But while the two musical
objects are indeed presented by the score, their relation itself is not.
If I want to formalise the logic of musical
discourse, in other words to treat musical relations, present but not
presented, between musical objects (which, themselves, are at the same time
present and presented by the score), it is necessary for me to undertake an
initial musicianly “formalisation” of musical discourse – I will call it
musicianly categorisation – capable of being then formalised in the framework
of our hexagon of oppositions.
Musicianly
categorisation
This categorisation will result from the three
principles affirmed above.
It goes without
saying that it is the musician – not music – that affirms them… in matters of
music.
The musical variation could take two
forms: that of alteration of the same object (via its repetition: A→A’) or that
of a contrast (A/B).
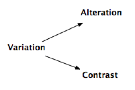
Alteration, inherent in the repetition of a musical
object, has for its contradiction the fixity that is attached to the unicity of a non-repeated
object, of an object only announced a single time, or in other words an hapax
H.
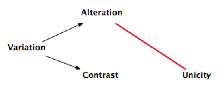
In the same way, variation has for its contradiction an invariance, which sums up two
possible modalities: the fixity of the object presented only once (the unicity
of
the hapax H) or the fixity of the simple repetition (A repeated
remains indeed A – beyond its variant A’ [4]):
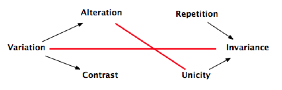
Repetition is distinguished here from variation: variation
transforms an object internally (as in our fugue where the response transforms
the subject by a transposition and a mutation) whereas repetition contents
itself with taking up the identical again (but by displacing it: between two
voices, chronologically). The figure of alteration (varied repetition
or variation associated to a repetition) sums or collects together these two
possibilities:

Hexagons…
Let us inscribe all this in a “philosophico-logical” hexagon:
Let us complete our formalisation by adding a centre that will suggest
its implicitly Borromean logic:[6]
the notion of properly musical “discursivity” is naturally situated at the
heart of this formalisation.
And we can detail this hexagon thus:
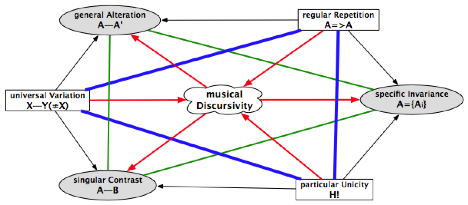
On the side of the triangle of contraries that link together (in blue)
the three figures of the conjunction or the product, we have:
· the principle of
universal variation (the musical discourse as a train of variations: Y, which
follows X, always differs from X, in one way or another) projects itself on the
one hand towards a general alteration (when A is redeployed, it is ipso
facto varied: A→A’) and on the other hand towards a singular contrast
(when what follows A is a completely different object B: A→B);
· regular repetition
(in music, the discursive regularity consists in repeating) projects itself on
the one hand towards a general alteration (repetition alters the repeated
object A) and on the other hand towards a specific invariance (which allows for
the recognition of the object A repeated in its series of alterations Ai
and by doing so allows for the differentiation of it from B);
· the particular
unicity of the hapax (H is only announced once) projects itself on the one hand
towards a particular form of invariance (that which is attached precisely to
the unique presentation) and on the other hand towards a particular aptitude
for creating discursive contrast (in the train of A).
On the side now of the triangle of subcontraries that link together (in
green) the three figures of summation or of gathering together:
· general alteration (proper to our
first principle of differentiation: A repeated is varied in A’) is the sum of repetition (reprise) and variation;
· the singular contrast (proper to our
principle of the required middle) is the sum of the variation of the objects set
in train by the discourse along with the unique presentation proper to the
object H;
· specific invariance (that allows for
the regrouping of the objects into related families) is the sum of the
particular type of hapax H and the aptitude of the regularly repeated objects.
This generates a family of related objects.
The
stakes of this third hexagon?
How does this formalisation allow us to better understand what “musical
discourse” means?
To
develop?
Our three initial principles have indicated to us that the composition
of a musical discourse involves posing together (com-posing) three terms: an
initial musical term A, its alteration A’ and another term B: {A, A’, B}.
But of course, to compose is not simply to pose these objects one up
against the other, it is above all to “develop” them; it is by this that one
can recognise a composer: not so much by his capacity to invent beautiful and
immutable melodies but more so by his capacity to develop the more banal motifs
and to make real musical use of them.
Our hexagon indicates then that to compose is to develop the initial
triple disposition by forming a simultaneous play of variations (or internal
deformations of objects), repetitions (or simple displacements of objects) and
of unique interventions attached to this or that object-hapax.
To compose is thus to knot together these three ways of giving each
object a future in the work (a future at work) in a logic that we could in
fact conceive as Borromean since:
· the quotient of
discursivity by repetition is indeed contrast[7]
(which is the sum of variation and the unique presentation);
· the quotient of
discursivity by variation is indeed invariance (which is the sum of the unique
presentation and repetition);
· the quotient of
discursivity by the unique presentation of H is indeed alteration[8]
(which is the sum of repetition and variation).
Two
musicianly positions on musical discourse…
In sum, which musical stakes are hidden behind this little formal game?
What does this hexagonal formalisation teach us about properly musical
discursivity?
First of all, it reminds us that musical operations on objects are more
important that the musical objects themselves: the composition of a musical
discourse plays itself out less in the choice of the object mobilised (motifs,
harmonies, “themes,” instruments, rhythms…) than in the compositional handling
that confers a musical destiny on these objects. But this the musician already
knows: the hexagon only formalises this conviction.
But above all this formalisation clarifies a musical duality that, in
our hexagon, takes the form of the contradictory[9]
duality between contrary products (here written within rectangles) and
subcontrary sums (here written within ovals), a duality that could be seen as
that which relates on the one hand what is produced by the score and on the
other what is summed by the play of the performer: whereas the composer (the
one who is found at the origin of the score) thinks in terms of variation, repetition, and unicity (what is it that I
should repeat, what is it that I should vary, and what is it that I should only
state once?), the interpreter (and necessarily then the auditor whose labour
consists ultimately in living the work as rendered sensible by the performer)
thinks in terms of alteration, contrast and invariance: what is it in
this discourse that remains the same, what is it that forms a contrast and what
is it that is altered?
Hence the idea of figuring our hexagon slightly differently, by
regrouping, as we have done above for our hexagon of timbre and rhythm, to have
on one side the products, and on the other the sums:
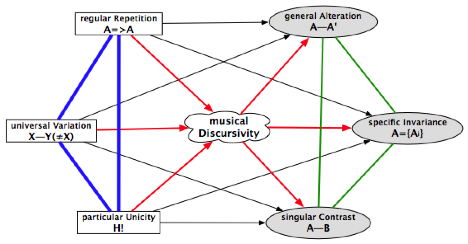
The triangle of the contraries (in blue) figures here as the labour of
the score; the triangle of the subcontraries figures by contrast the labour of
the interpretation (and subsequently the audition).
Thu we find again the
intuition evoked before that the score, rooted in the writing of solfege,
operates in the framework of an intuitionist logic and that interpretation,
attached to sensible labour (proper to the body and the ear), labours in the
framework of a paraconsistent logic.
We could then read this “sketch” from left to right (all the arrows are
found here oriented in this sense)[10]
as a path going from construction (proper to written material) towards
expression (proper to sonic material).
In sum, this arrangement of our hexagon would figure, under the form of
the opposition of left/right, the dialectic of the eye and the ear, of the read
and the heard, the written and the sonic, the score and the audition.
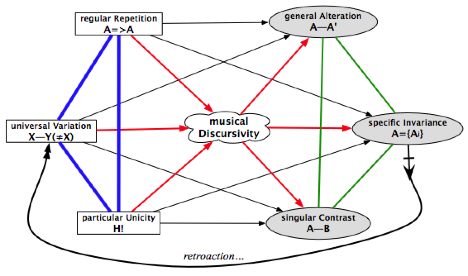
It would then be necessary to complete this “sketch”[11]
by directly linking together “specific invariance” and “universal variation”[12]
in order to formalise a retroactive component of the labour (that
of the performer or auditor) upon the comprehension of the score and its
capacity to project different dimensions at work in the musical discursivity:
I will stop here at these considerations, which remain, you will have
understood, open and only held in a provisional state of my own research into
what logic and negation could mean in music.
*