[Introduction]
Le problème est le suivant : est-il possible de
décrire au sein des mathématiques une structure qui soit comme un
premier dessin de la forme temporelle des phénomènes sensibles ?
Ce problème est difficile car, plus encore que
l’espace, le temps semble lié à l’existence sensible
de l’Univers.
La tâche ne consiste pas à introduire le
changement ou le devenir dans le monde immuable des vérités
mathématiques mais à distinguer du temps sensible une forme
abstraite de temps.
D’où plusieurs moments d’une analyse
régressive :
* décrire
les propriétés sensibles du temps qui s’inscrivent dans les
équations de la physique mathématique ;
* montrer
que la structure mathématique de ces équations leur vient non du
domaine physique auquel elles s’appliquent mais du domaine
mathématique dont elles procèdent ;
* chercher
ensuite la portée dialectique de ces résultats.
Au fur et à mesure de ce parcours, le temps se
dépouillera ainsi de son aspect mouvant et vécu et nous arriverons
jusqu’à ce germe incréé qui contient en lui
les éléments d’une genèse ontologique du
devenir sensible. Le temps physique apparaîtra comme étant la
réalisation sensible d’une structure qui se manifeste
déjà dans le domaine intelligible des mathématiques.
Le temps sensible et la physique mathématique
Par delà la distinction entre mécaniques
(classique, relativiste, quantique et ondulatoire), on peut dégager de communes
conditions de structure qui opèrent la liaison du sensible et de
l’intelligible.
Les faits expérimentaux dont on part sont les trois
propriétés sensibles suivantes du temps :
1)
irréversibilité [ou orientation] :
le temps s’écoule toujours dans le même sens ;
d’où une dissymétrie du temps par rapport à
l’espace ;
2)
étalement dans le temps [ou direction] :
les objets persistent au cours du temps qui est continu ;
3)
paramétrage
d’évolution dynamique : les grandeurs autres que le temps varient en fonction
du temps.
Les propriétés 1 et 2 engendrent la direction
orientée [soit la propriété géométrique du temps] qui est dissymétrique par rapport
aux dimensions de l’espace.
La troisième propriété désigne
la propriété dynamique du
temps (facteur d’évolution) qui ne le concerne
qu’indirectement et qui n’implique par elle-même aucune
direction temporelle, aucune irréversibilité.
Au total, on peut donc distinguer deux sortes de
propriétés sensibles du temps :
· Propriétés
géométriques : direction et orientation.
· Propriétés
dynamiques : évolution.
Voyons d’abord l’aspect mathématique que
prennent les propriétés sensibles du temps au sein des diverses
théories physiques.
Temps comme direction orientée
1) Aspect algébrique
Dans la synthèse spatio-temporelle de la
relativité restreinte, le temps joue un rôle équivalent
à celui des coordonnées d’espace mais différent par
son signe ; cf. la distance de deux points est :
ds2 = dx2 + dy2 + dz2 – c2dt2
2) Aspect
géométrique
Interprétation géométrique de cette
formule : par un cône à deux nappes, orienté vers
l’avenir, en chaque point de l’espace-temps.
D’où une dissymétrie posée de
deux façons équivalentes :
· algébrique : différence de signe dans
une forme quadratique (attachée à chaque point) ;
· géométrique : direction orientée
d’un cône (attaché à chaque point).
Ceci illustre les notions
solidaires de différence de signe (algèbre) et de direction
orientée (géométrie).
Temps comme paramètre dynamique
1) Aspect du
paramètre
Soit le cas simple d’un point dans l’espace
euclidien dont les trois coordonnées sont paramétrées par
le temps t.
Soit
· T
son énergie cinétique [T º 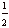 mv2],
mv2],
· V
son énergie potentielle,
· L
(x, y, z, t) la fonction de Lagrange avec L = T-V.
Principe (dynamique) d’Hamilton : si ce point se
déplace de A en B, la courbe C représentant sa trajectoire est
telle qu’elle maximise ∫L.dt
le long de C, soit :
d∫L.dt = 0
[Hamilton]
On peut déduire de ce principe d’extremum
toutes les lois de la mécanique classique .
Si une particule a pour coordonnées qi avec qi = dqi/dt. Soit les
quantités pi = ∂L/∂qi. Alors
l’énergie H de la particule est donnée par la formule
H(qi, pi, t) =
∑piqi - L(qi, qi, t)
et on peut déduire du principe d’Hamilton les
équations canoniques :
dqi/dt = ∂H/∂pi et dpi/dt = - ∂H/∂qi
Lorsqu’il y a conservation de l’énergie,
on peut déduire du principe dynamique d’Hamilton le principe de
moindre action de Maupertuis :
d∫ .ds = 0 [Maupertuis]
.ds = 0 [Maupertuis]
où  représente le vecteur quantité de mouvement et ds l’élément d’arc de courbe
parcouru.
représente le vecteur quantité de mouvement et ds l’élément d’arc de courbe
parcouru.
Or si le temps figure comme paramètre
d’évolution (dt) dans le
principe d’Hamilton, ce rôle est joué dans le principe de Maupertuis
par l’élément d’arc de courbe (ds).
Ainsi le fait pour le temps d’être le
paramètre d’évolution est indépendant de ses
propriétés géométriques.
2) Aspect
géométrique de dimension
Cette indépendance [formelle] des propriétés dynamiques et
géométriques correspond cependant à une équivalence
rigoureuse dans le cadre de la mécanique classique. On peut en
effet exprimer le principe dynamique d’Hamilton sous une forme
géométrique où le temps figure comme coordonnée
affectée d’un signe différent.
Passons pour cela dans un espace à n+1
dimensions : n coordonnées spatiales qi et le temps t.
Soit L la fonction de Lagrange
généralisée : L = T – V
et soit E l’énergie du système :
E = T + V.
Soit pi = ∂L/∂qi.
On a vu alors que E = ∑ piqi – L.
On en déduit :
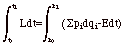
avec P0(q0i, t0) et P1(q1i, t1)
L’expression ∑ piqi – E.dt dont
l’intégrale est ici minimale peut être regardée comme
le travail d’un vecteur qui aurait
· pour
composantes spatiales les n composantes
ordinaires (de la quantité de mouvement),
· pour
composante temporelle l’énergie changée de signe.
On retrouve bien ainsi une synthèse spatio-temporelle
analogue à celle de la relativité restreinte où le temps
impose une différence de signe par rapport à l’espace.
*
L’équivalence entre
propriétés géométriques et propriétés
dynamiques que l’on vient de trouver dans la mécanique classique
va devenir une opposition dans le cadre de la mécanique ondulatoire.
Cf. principe fondamental de cette étude :
lorsqu’il s’agit de deux notions distinctes, leur
équivalence ou leur opposition apparaissent sur le même plan comme
postérieures au fait de leur simple dualité.
Nous appellerons Idée le problème de la détermination de liaison à
opérer entre notions
distinctes. C’est dans ces conditions que nous concevons
l’existence d’une théorie des Idées, d’une dialectique,
commune à la mécanique ondulatoire et à la mécanique
classique, alors même que la première précipite en opposition
des notions dont l’accord est évident en mécanique
classique.
Mécanique ondulatoire.
Il y a désormais deux aspects non unifiés du
temps :
1) Aspect dynamique
Le temps intervient comme paramètre
d’évolution dans l’étude des probabilités
attachées à n’importe quelle grandeur physique, non comme
coordonnée. Cf. ces probabilités sont fonction du temps et
c’est pour cela que le système évolue.
2) Aspect
géométrique
La 4° relation d’Heisenberg reliant énergie
et temps (∆E.∆t ≥ h) est très
différente des trois relations d’incertitude qui relient
coordonnées d’espace q et quantités de mouvement p
(∆q.∆p ≥ h) car elle définit non une erreur
commise sur la mesure de E mais la durée minima de l’expérience
permettant d’attribuer à l’énergie E du corpuscule
une valeur à ∆E près. D’où une
différence de nature entre temps et espace : les lignes de l’univers sont bien orientées
dans le sens du temps.
Au total on semble bien avoir ici deux temps distincts !
*
On peut dégager une source mathématique
à cette dualité du temps dans la mécanique ondulatoire.
[…]
La théorie des équations aux dérivées
partielles.
[Reproduction du
texte même de l’article]
Nous avons vu les
équations de la mécanique mettre en évidence deux
aspects du temps, parfois équivalents, parfois distincts, mais
l’un et l’autre adaptés par leurs caractères intrinsèques
aux dissymétries sensibles de l’expérience. Le
résultat fondamental de la déduction a priori que nous allons exposer est alors le suivant : cette
dualité des aspects du temps, doués chacun de ces
dissymétries propres, n’apparaît pas seulement dans
l’application des mathématiques à l’univers physique,
c’est-à-dire en mécanique, mais existe déjà
au niveau des mathématiques pures, indépendamment de tout souci
d’application à l’univers. Quelle que soit l’origine
dialectique de cette dualité des temps que nous trouverons
inhérente à la théorie des équations
différentielles et des équations aux dérivées
partielles, la mécanique n’apporte, en ce qui concerne le
problème du temps, aucun arrangement dont le schéma ne se laisse
apercevoir dans les abstractions pures dont elle est l’application. Le
temps physique sous toutes ses formes n’est que la réalisation
sensible d’une structure qui se manifeste déjà dans le
domaine intelligible des mathématiques.
La méthode que nous
allons suivre dans cette démonstration est une méthode
d’analyse régressive. Nous procèderons du concret à
l’abstrait, du composé au simple, pour reporter toujours le
nœud du problème à un niveau plus élevé dans
la hiérarchie des Idées ; et c’est ce rattachement de
données empiriques à une structure idéale qui constitue
pour nous la déduction a priori
des dissymétries sensibles relatives aux temps. Cette méthode
présente sur les synthèses déductives du temps
qu’ont essayées les philosophies idéalistes du XIXe
et du XXe siècle un avantage, à nos yeux
considérable : nous n’opérons pas arbitrairement une
déduction a priori du
temps, nous observons, dans l’ordre de l’univers, les étapes
constituées de cette déduction.
Une pareille exigence
d’analyse explique les raisons pour lesquelles nous envisagerons la
théorie des équations aux dérivées partielles avant
la théorie des équations différentielles. Les
équations de la physique mathématique sont en effet
généralement des équations aux dérivées
partielles de sorte que la théorie générale de celles-ci
constitue comme le premier domaine où retrouver le jeu pur des relations
que soutiennent entre eux les différents aspects du temps physique.
Considérons ()
l’équation aux dérivées partielles du premier ordre,
à deux variables indépendantes, F(x1, x2, u, p1, p2) = 0,
où u est une fonction inconnue
des deux variables x1 et x2 et où p1 = ∂u/∂x1, p2 = ∂u/∂x2.
On suppose
(∂F/∂p1)2 + (∂F/∂p2)2 ≠ 0.
En chaque point de
l’espace à trois dimensions x1, x2, u, cette équation définit une famille de
plans tangents possibles à une surface intégrale u(x1, x2) passant par
ce point. Cette famille de plans enveloppe un cône, défini en
chaque point de l’espace envisagé, le cône de Monge attaché à ce point,
de sorte que l’équation F = 0 peut être
considérée comme associant à tous les points de
l’espace un cône ou encore un faisceau de directions
caractéristiques, les
génératrices du cône de Monge
de ce point. Intégrer l’équation proposée consiste
à trouver une surface tangente en chaque point à une direction
caractéristique passant par ce point, et cette intégration se
fait par la considération des courbes caractéristiques de l’équation. Voici ce qu’il
faut entendre par là : une courbe caractéristique de
l’équation F = 0 est tangente en chacun de ses points
à une direction caractéristique passant par ce point. On
démontre qu’une surface intégrable u(x1, x2) de
l’équation F = 0 est engendrée par une famille de
courbes caractéristiques, de sorte que le problème de
l’intégration de l’équation aux
dérivées partielles proposée est ramené au
problème de l’intégration des équations
différentielles qui définissent les courbes
caractéristiques de cette équation. Il est très important
pour nous de considérer les équations différentielles de
ces caractéristiques. On considère pour cela en général
les coordonnées x1, x2, u des points d’une courbe de l’espace
envisagé, comme des fonctions x1(t), x2(t), u(t) d’un
paramètre t. Les courbes
caractéristiques de l’équation F(x1, x2, u, p1, p2) = 0
satisfont alors à un ensemble de trois équations
différentielles dont nous ne retenons ici que les suivantes () :
(I) dx1/dt = ∂F/∂p1 , dx2/dt = ∂F/∂p2 .
Une surface
intégrale est engendrée avons-nous dit par des courbes
caractéristiques, de sorte qu’étant donnée une
courbe caractéristique définie par les équations
différentielles (I), cette courbe peut être assujettie à la
condition supplémentaire d’être située sur une
surface intégrale de l’équation F = 0. Cette
condition donne naissance à deux nouvelles équations que nous
écrirons sous la forme simplifiée qu’elles prennent lorsque
la fonction F ne contient pas la variable u :
(II) dp1/dt = - ∂F/∂x1 , dp2/dt = - ∂F/∂x2 .
La détermination
des surfaces intégrales est donc ramenée à
l’intégration d’un système d’équations
différentielles où nous ne retiendrons que les équations
(I) et (II) écrites sous la forme :
(III) dxi/dt = ∂F/∂pi ; dpi/dt = - ∂F/∂xi .
Les équations (III)
ont exactement la forme des équations canoniques de la dynamique du
point matériel lorsque F
représente l’énergie de la particule, et t le temps. C’est là dans la déduction
a priori des lois de
l’univers sensible un résultat d’une importance
considérable que de voir les équations des trajectoires de la
dynamique résulter a priori,
sans hypothèse physique spéciale, du problème de
l’intégration des équations aux dérivées
partielles. L’espace géométrique x1, x2, u contient ainsi comme à l’état de
possibles, avec ses directions et ses courbes caractéristiques de
l’équation F = 0, la forme de trajectoires et la loi
dynamique de mouvements qu’y prendront des particules matérielles
lorsqu’une interprétation physique, transmuant la fonction F en énergie et le paramètre t en variable temporelle, projettera ainsi tout
armé dans l’existence sensible un univers mathématique
déjà muni de toute la richesse d’organisation
nécessaire.
Nous n’avons
jusqu’à présent montré que la possibilité de
déduction a priori des lois de la
mécanique où le temps intervient comme paramètre
d’évolution ; nous arrivons maintenant au point central de la
démonstration annoncée plus haut en montrant au sein de la
même théorie des équations aux dérivées
partielles la genèse d’une conception dimensionnelle du
temps physique distincte en son principe de la conception paramétrique
mais servant à résoudre les mêmes problèmes.
Plaçons-nous dans le cas général d’un espace
à n+1 dimensions et
envisageons l’équation aux dérivées partielles
suivante, où la fonction F ne contient pas explicitement la fonction u(x1…xn, xn+1,)
cherchée () :
F(x1…xn+1, p1…pn+1) = 0.
Nous allons, suivant en
cela l’exposé de M. Courant
dans le tome II des Methoden der Mathemastischen Physik de Hilbert
et Courant, distinguer une variable, par exemple xn+1 et
résoudre l’équation proposée par rapport à la
dérivée correspondante pn+1.
Nous obtenons
l’équation :
pn+1 + H(x1…xn, xn+1, p1… pn) = 0
(pn+1 = ∂u/∂xn+1 ; pi = ∂u/∂xi ;
i = 1…n).
L’expression pn+1 + H
remplace donc l’expression F de
l’équation donnée. Le premier groupe
d’équations des courbes caractéristiques, dxi/dt = ∂F/∂pi avec
i = 1…n+1, donne pour i = n+1, dxn+1/dt = 1.
La variable xn+1 est
donc constamment égale, à une constante additive près, au
paramètre t et on peut remplacer
ce paramètre t de la
théorie précédente par la variable indépendante
distinguée dans la nouvelle. Les équations
caractéristiques s’écrivent alors dxi/dxn+1 = ∂H/∂pi ; dpi/ dxn+1 = - ∂H/∂xi ;
i = 1…n, et l’on retrouve bien la forme abstraite des
équations canoniques d’Hamilton.
Dans l’espace à n+1
dimensions défini par les variables x1…xn+1 le
fait de résoudre l’équation proposée par rapport
à une dérivée partielle concernant l’une de ces
variables fait jouer à cette variable le rôle de variable
temporelle. Il y a dans ce cas équivalence absolue entre le rôle
de paramètre et le rôle de coordonnée
dimensionnelle d’une même variable distinguée, mais il
n’en subsiste pas moins le fait que la théorie purement
mathématique des équations aux dérivées partielles
permet ainsi la naissance de deux conceptions différentes d’une
même variable qui sont à l’origine de la dualité des
propriétés sensibles du temps.
[…]
Il nous reste encore un
point à envisager. Nous venons de retrouver a priori dans la théorie des équations aux
dérivées partielles la distinction du temps paramètre et
du temps coordonnée ; il nous faut maintenant montrer a
priori comment le temps
coordonnée intervient dans une synthèse spatio-temporelle
affectée de cette dissymétrie spéciale par rapport
à l’espace qui se manifeste par une différence de signe. Le
même problème nous permettra à la fois de retrouver la
distinction des deux conceptions du temps et la dissymétrie
spéciale du temps dimensionnel. Nous envisagerons pour cela la
théorie des équations aux dérivées partielles du
second ordre, et nous nous restreindrons au cas où ces équations
sont linéaires, c’est-à-dire de la forme
(V) ∑aikuik + ∑biui + cu + d = 0
avec uik = ∂2u/∂xi∂xk ; ui = ∂u/∂xi, u étant la fonction inconnue cherchée.
On démontre
qu’on peut associer à toute équation de ce genre une
forme caractéristique ∑aiXi2 (i =
1…n) avec ai = ±1.
La forme caractéristique associée aux équations qui
décrivent une propagation est dite de type hyperbolique ;
elle est composée de n-1
carrés positifs et d’un carré négatif : X12 + … + Xn-12 - Xn2. Nous ne nous occupons ici que du cas
hyperbolique. Comme dans le cas des équations aux dérivées
partielles du premier ordre, une surface intégrale de
l’équation (V) est engendrée par des variétés
caractéristiques j = 0 qui satisfont ici à
l’équation ∑aikjijk = 0,
et ces variétés caractéristiques sont à leur tour engendrées par des rayons
caractéristiques que
définissent dans l’espace à n dimensions les équations différentielles
dxi/dt = ∑aikjk (pour
k = 1…n). On peut à nouveau distinguer une variable xn et
résoudre l’équation j = 0 par rapport
à xn
pour obtenir xn = y(x1…xn-1). Dans ces
conditions l’équation des rayons donne : dxn/dt = 1
et l’on peut à nouveau identifier la variable dimensionnelle avec
le paramètre d’évolution. Un exemple concret montrera
néanmoins le caractère propre de chacun de ces deux aspects du
temps. Considérons l’équation d’onde classique u44 – u11 – u22 – u33 = 0.
Dans l’espace-temps à quatre dimensions on peut définir une
distance de deux points ds2 = dx42 – dx12 – dx22 – dx32.
Les droites de longueur nulle (ds = 0) issues d’un
point quelconque définissent le cône caractéristique
attaché à ce point et toute direction située à
l’intérieur du cône satisfait à
l’inégalité ds2 > 0. En
particulier, pour l’axe des temps x4 défini par les relations dx1 = dx2 = dx3 = 0,
on a bien dx42 > 0,
et ceci montre le caractère « orienté » de
la variable x4
dans son rôle de temps dimensionnel.
Plaçons-nous maintenant dans l’espace à trois dimensions.
La distance de deux points est donnée par la formule dr2 = dx12 + dx22 + dx32.
Si t désigne dans ce cas la
longueur comptée sur un rayon à partir de l’origine, la
vitesse de propagation étant prise pour unité, les surfaces t =
constante définissent les surfaces
d’onde qui représentent le front de l’onde à chaque
instant. Il y a bien équivalence dans les résultats obtenus entre
le temps, dimension de l’espace à quatre dimensions, et le temps
longueur dans l’espace à trois dimensions, mais chacune de ces
deux conceptions du temps apporte avec elle un élément
propre : la conception du temps dimension orientée est liée
à l’existence d’une différence de signe dans les
termes d’une somme de carrés ; la conception paramétrique
est liée aux notions cinématiques de vitesse et de déplacement.
La Théorie des équations différentielles et la
topologie
Les relations que soutiennent entre elles les
différentes notions enlacées dans la théorie des
équations aux dérivées partielles, deviennent beaucoup
plus intuitives dans la théorie des équations
différentielles. Le sens géométrique des équations
aux dérivées partielles que nous avons envisagées
était en effet le suivant : l’équation donnée
définit en chaque point d’un espace un cône
caractéristique de ce point et l’intégration de
l’équation consiste à trouver des courbes et des surfaces
tangentes en chaque point au cône caractéristique de ce point. La
distinction du temps dimension et du temps paramètre se rattache dans
une certaine mesure à la dualité suivante : le sens
d’ouverture du cône caractéristique assigne en chaque point
de l’espace un rôle privilégié à une direction
qu’on peut considérer comme une direction temporelle, et
d’autre part les courbes et surfaces tangentes à ce champ de
cônes sont fonction d’un paramètre que l’on peut
considérer également, mais en un autre sens, comme une variable
temporelle.
Dans la théorie des équations
différentielles, la situation est encore plus simple.
Soit l’équation dy/dx = f(x,y).
Cette équation
définit dans le plan (x,y) un champ de directions (une direction est
attachée à chaque point) et les solutions de cette
équation sont les courbes tangentes en chaque point à la
direction qui passe par ce point.
L’interprétation
géométrique de la théorie des équations différentielles
met donc bien en évidence deux réalités distinctes : le champ de directions et les
courbes intégrales.
Si maintenant les variables x et y sont rapportées
à un même paramètre t, on n’a plus seulement une direction
en chaque point (x, y) mais aussi un sens c’est-à-dire un vecteur
(une direction orientée).
Soit par exemple l’équation (I)
dy/dx= Q(x,y)/P(x,y). À certaines conditions sur P et Q, elle
définit un champ de directions.
Si on paramètre x
et y par t, on a au lieu de (I) le système suivant :
(II)
dx/dt = P(x,y) et dy/dt = Q(x,y)
Ce système définit non plus seulement une
direction en chaque point mais un sens, c’est-à-dire un vecteur
qui lui est attaché.
Les points d’indétermination où
P = Q = 0 constituent alors les singularités du
champ de vecteurs (que Poincaré classe en cols, nœuds, foyers,
centres).
On a donc à nouveau deux réalités
mathématiques essentiellement distinctes (champs de
vecteurs — cf. l’aspect dimensionnelle du temps —
et courbes intégrales — cf. sa paramétrisation des
évolutions) même si elles sont complémentaires puisque
définie par la forme des courbes dans leur voisinage.
On peut montrer que les propriétés
paramétriques du temps peuvent ne se rapporter qu’à une
évolution limitée dans un intervalle bien défini du temps
sans référence à aucune structure d’ensemble alors
que les propriétés dimensionnelles (géométriques)
ont un sens cosmogonique et reflètent la forme générale de
l’Univers.
En effet on démontre que l’existence d’un
invariant d’univers (en l’occurrence une forme quadratique du type
de celle qui définit la distance dans notre espace-temps à quatre
dimensions) est équivalente à l’existence de champs sans
singularités. Or si un univers à quatre dimensions est compact et
tel que l’on puisse y définir une distinction entre passé
et avenir en chaque point, alors on est assuré qu’un tel champ
continu de vecteurs sans singularité y existe. La
détermination du sens du temps dans l’univers est bien solidaire
de la structure d’ensemble de l’univers.
*
On a donc les résultats suivants :
1. En matière de temps
géométrique (champs de vecteurs)
* il y a une
liaison nécessaire entre l’existence d’une direction
privilégiée en chaque point d’un univers
géométrique et le défaut d’une forme quadratique (la
« différence de signes ») ;
* la
distinction en chaque point d’une direction privilégiée
n’est possible que si l’Univers satisfait à certaines
conditions globales, en particulier de compacité : il ne doit pas y avoir de trou dans la durée des
choses et dans l’ouverture du temps vers l’avenir.
Ainsi l’aspect géométrique du temps
est lié à la forme générale de tout
l’univers, c’est un temps cosmogonique.
2. En matière de temps dynamique
(courbes intégrales paramétrables), on peut interpréter
différents problèmes en terme de temps :
· le
problème du déterminisme : c’est le cas des
équations où la connaissance des données initiales suffit
à connaître l’évolution ultérieure ;
c’est une sorte de déterminisme local, de proche en proche ;
· le
problème de la finalité : ici la connaissance des
données initiales ne suffit plus ; il faut y ajouter la
connaissance des conditions finales ;
· le
problème du retour des choses : c’est le cas des trajectoires
fermées.
Au total la distinction
mathématique du temps cosmogonique et du temps dynamique est donc
l’expression d’une dualité correspondant à une
structure intime des choses qui a sa source dans la structure des Idées.
––––
