Du partage moderne/contemporain dans le livre de Fernando Zalamea

(« Philosophie systématique de la mathématique contemporaine », Hermann, 2018)

 

Séminaire mamuphi, 16 novembre 2018

 

 

- François Nicolas -

 

[ pdf ]

 

Ma contribution est modeste : je propose d’interroger ce livre, tout à fait extraordinaire, sur la portée du partage moderne/contemporain qui l’organise. La distinction des mathématiques modernes et contemporaines est en effet au principe de cet ouvrage et l’on ne peut, concernant un travail philosophique, examiné qui plus est dans le cadre de mamuphi, séparer totalement cette distinction de celle qui opère plus généralement en matière d’arts (et plus spécifiquement en matière de musique) sous les mêmes signifiants classique/moderne/contemporain.

 

Repartons pour cela de ce schéma (en diagramme de Venn) [1] :

 

 

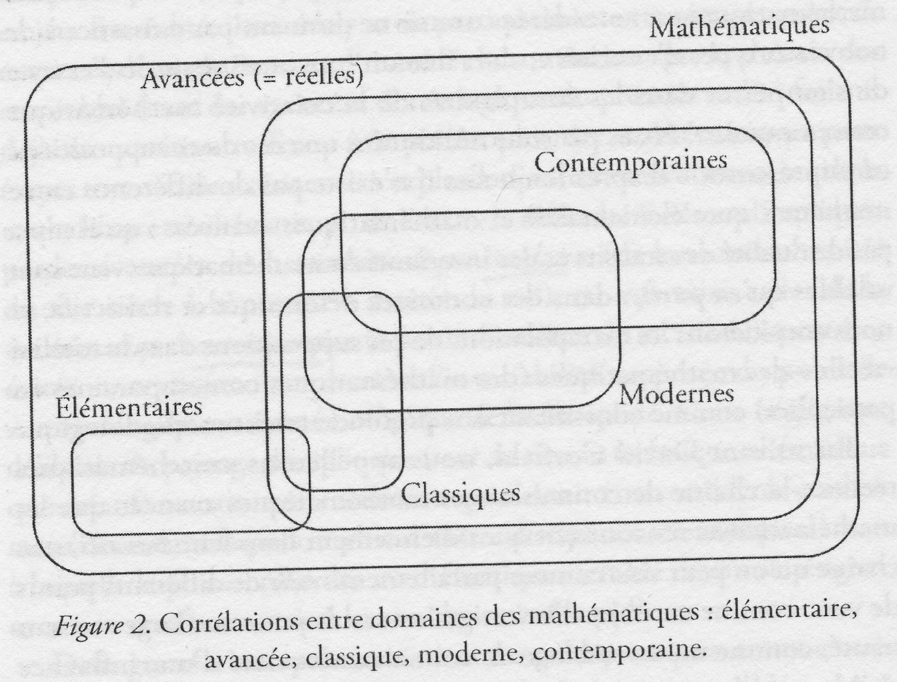
Il oppose en premier lieu mathématiques élémentaires et avancées ou réelles.

En second lieu, il périodise les mathématiques avancées en trois séquences enchaînées : classiques/modernes/contemporaines.

 

Suivant la logique diagrammatique de ce schéma, on dira que

1)     les mathématiques contemporaines sont au mathématiques modernes ce que celles-ci sont aux mathématiques classiques et ce que ces dernières sont aux mathématiques élémentaires :

 

 

2)     les mathématiques contemporaines prolongent les mathématiques avancées qu’ont inauguré les mathématiques classiques : à ce titre, le rapport mathématiques classiques/élémentaires diffère des suivants en ce qu’il est le seul à engager un nouveau régime de mathématiques (ici dites « avancées »), soumis à périodisation interne :

 

élémentaires ≠ {classique → moderne → contemporain}

 

3)     chaque nouvelle étape s’enchaîne à la précédente par intersection : il n’y a ni séparation complète entre l’ancien et le nouveau, ni inclusion intégrale de l’ancien dans le nouveau mais relais pris par une section commune 

 

 

intersection ≠ {séparation ou inclusion}

 

Remarquons au demeurant une petite intersection supplémentaire entre mathématiques contemporaines et classiques, intersection secondaire qui dissymétrise l’enchaînement chronologique et tend à mieux solidariser le bloc « mathématiques avancées ».

 

On va voir que cette forme d’enchaînement (par intersection commune) entre différentes périodes historiques procède d’une formalisation explicitement moderne et contemporaine puisqu’elle évoque aussi bien les recouvrements dans les atlas des variétés riemanniennes (mathématiques modernes) que les recollements des faisceaux (mathématiques contemporaines).

En ce sens, on peut dire que ce schéma réduplique [a] son enjeu puisqu’il formalise sa périodisation des mathématiques selon l’esprit même des notions sur lesquelles elle débouche : il ajuste son mode d’exposition (d’énonciation) à ce qu’il s’agit d’exposer (à son énoncé).

 

 

Tentons de transposer ces trois caractérisations en musique, même si ce type d’analogie est fort périlleuse – elle va nous servir, non à éclairer la musique (qui, bien sûr, ne marche pas du même pas que les mathématiques) mais bien plutôt à rétroéclairer les partis pris de cette périodisation mathématique.

 

1)     La première caractérisation suggèrerait la formule suivante en musique :

 

 

Elle induirait donc l’existence d’une musique contemporaine (presque [b]) aussi distincte de la musique moderne que celle-ci l’est de la musique classique.

Cette proposition circule en effet, sous sa modalité la plus commune d’une musique postmoderne (événementiellement ouverte en 1968 par Sinfonia de Berio) tout de même que l’art dit contemporain aime à se présenter comme dépassement des arts plastiques modernes (peinture et sculpture) à partir de la Biennale de Venise de 1964 [c].

Cette manière de voir n’est nullement la mienne : je soutiens bien plutôt que la musique dite contemporaine constitue une nouvelle partie de la musique moderne – sa partie précisément « contemporaine » - et que l’on a donc, à très gros traits, si l’on pose : préclassique = modal ; classique = tonal ; moderne = atonal [d] ; contemporain = moderne d’aujourd’hui, la formule suivante en musique :

 

 

Première dissonance donc.

 

 

2)     La deuxième caractérisation suggèrerait la formule suivante en musique :

 

préclassique ≠ {classique → moderne → contemporain}

 

Cette proposition s’accorderait davantage au point de vue suivant, qui est tout particulièrement celui de Pierre Boulez [e] :

 

la musique moderne est la musique classique contemporaine

(à entendre ainsi : la musique moderne continue la musique classique dans le monde contemporain).

 

Mais dans ce cas, on ne compte plus exactement 3 (classique/moderne/contemporain) mais plutôt 2 (classique/moderne).

Seconde dissonance donc.

 

3)     La troisième caractérisation suggèrerait la formule suivante en musique :

 

intersections ≠ {séparation ou inclusion}

 

Cette manière de voir ne me semble pas s’accorder au dynamisme historique de la composition musicale. En effet je poserais volontiers quelque chose comme :

 

 

Cette manière de voir mobilise les trois modalités formelles d’enchaînement, dans une logique qui évolue progressivement d’une disjonction complète à une figure d’extension (donc d’inclusion).

Troisième dissonance donc.

 

 

On m’objectera bien sûr : pourquoi périodisations mathématiques et musicales - plus généralement scientifiques et artistiques - devraient-elles s’accorder ? En effet. Et d’ailleurs mon propos, en les rapprochant, n’est pas de les accorder mais de les mettre en raisonances mamuphiques, c’est-à-dire de les rapporter (sous condition de la philosophie) en sorte de mieux examiner leurs autonomies relatives.

Je précise donc mon propos : il s’agit d’interroger ce grand livre sous l’angle d’une intellectualité musicale particulière qui, faisant jouer la conceptualisation du discours philosophique tenu sur les mathématiques, en fait ressortir certains ressorts subjectifs [f], certaines intensions fondamentales et lignes de force.

Il me faut donc examiner de plus près la périodisation mathématique au principe du travail philosophique de Zalamea et pour cela interroger ses conditions de possibilité et ses points d’ancrage, tant mathématiques que philosophiques.

 

 

Au risque de trop simplifier un discours d’une très grande richesse – dois-je préciser que je n’ai pas l’immense culture mathématique de l’auteur et que ma connaissance de la pragmatique peircienne reste trop élémentaire pour que je m’autorise une discussion serrée de ses orientations – je voudrais interroger ce livre selon l’hypothèse qui me semble globalement l’animer : la notion de faisceau inaugure et enveloppe les mathématiques contemporaines comme celle de groupe a inauguré et enveloppé les mathématiques modernes.

D’où, pour Zalamea, une périodisation contemporaine qui démarre dans l’après-guerre [g], un bon siècle donc après le début des mathématiques modernes autour de 1830 ou 1850 [h].

 

Remarquons, raisonances mamuphiques obligent, que ces deux moments mathématiquement cruciaux constituent des tournants généraux dans la pensée humaine :

-       inutile d’insister, je pense, sur l’importance générale du tournant 1848 pour toute l’humanité (politiquement [i], musicalement [j], philosophiquement [k], etc.) ;

-       tout de même, le tournant de l’après-guerre est décisif pour la musique [l], la politique [m] et la philosophie [n].

Raison supplémentaire d’interroger les manières de comprendre ces différentes périodisations relativement synchrones.

 

 

Je voudrais donc interroger la manière dont la périodisation du livre pivote sur cette notion mathématique de faisceau :

« La notion de faisceau mathématique est probablement le concept distinctif fondamental autour duquel l’élaboration des mathématiques contemporaines débute, avec un nouvel élan et tous ses instruments extraordinaires […] ; ainsi, la tentative de voir la mathématique à partir d’un faisceau de perspectives également complexes devient naturelle. » [2]

On notera la réduplication explicite : il s’agit de voir la mathématique des faisceaux selon un faisceau de perspectives : autrement dit, l’énonciation sur les faisceaux doit être faisceautisée tout comme, pour Pascal, l’énonciation sur l’humilité devait être humble §et non pas orgueilleuse).

 

Il me semble d’abord que Zalemea fait jouer à ce concept mathématique un triple rôle philosophique : pragmatiste (au sens du pragmaticisme de Peirce), logique (au sens d’une opposition à la logique classique) et synthétique (au sens cette fois d’une opposition à la philosophie dite analytique).

Ce triple rôle philosophique s’adosse explicitement aux propriétés mathématiques du faisceau de voisinage, recouvrement, cohérence et recollement - voir cette figure [3] :

 

 

Détaillons un peu comment.

 

Pragmatiste ?

Zalamea reconnaît, dans le travail du faisceau, une nouvelle manière mathématique de produire de l’Un à partir du multiple, manière mathématique qui consonne pour lui avec la manière pragmatique de Peirce d’unifier l’objet comme symbole.

La clef repose ici sur « la maxime du pragmatique ou du pragmaticisme » [4] qui connaît plusieurs formulations apparentées, qu’ici je paraphrase :

-       (1878) notre entière conception d’un objet se constitue par totalisation de ses effets pratiques ;

-       (1905) la signification complète d’un symbole consiste dans le total des modes de conduite rationnelle adoptant ce symbole en toute circonstance possible.

Ainsi, pour unifier en un tout globalement cohérent un multiple de pratiques particulières, locales et dispersées, la pragmatique opère comme le fait un faisceau « qui permet de produire des recollements globaux à partir d’informations locales cohérentes » [5].

En ce sens, la maxime pragmatiste de Peirce nous immerge « dans une sorte de faisceautisation épistémologique où la multiplicité différentielle locale est recomposée en une unité intégrale globale. » [6]

 

Logique ?

Le rôle logique repose sur l’opération faisceautique de recollement : deux voisinages sont recollés au moyen d’une partie commune (d’un recouvrement). Ceci présuppose donc que les termes à recoller ne sont pas entièrement disjoints, exclusifs l’un de l’autre mais qu’ils comportent une zone de coexistence (voir par exemple les figures d’intersection dessinées plus haut entre les différents types successifs de mathématiques), qu’ils se recouvrent donc partiellement.

On pourrait dire, en un vocabulaire que n’emploie pas Zalemea mais qui est compatible avec son propos : les voisinages, étant distincts, sont bien opposés mais ils le sont alors ni sous la forme classique de deux contradictoires (soit l’un soit l’autre, selon le principe du tiers-exclu), ni sous celle de contraires (si l’un, pas l’autre, avec possibilité tierce d’un ni l’un ni l’autre), mais sous celle de subcontraires (l’un ou l’autre, qui est partiellement l’un et l’autre). Autant dire que la logique faisceautisée de tels voisinages est d’inspiration paraconsistante ; d’où une logique « co-intuitionniste » [7] plutôt que classique ou intuitionniste.

Pour Zalamea, on a ainsi à faire à « un tournant du côté d’une logique réelle des voisinages, […] du côté d’une logique de faisceaux comme contrepoint à la logique classique » [8].

 

Synthétique ?

Zalamea s’intéresse enfin à la problématique mathématique du faisceau comme mise en œuvre intégrée d’une « triangulation » : « localité-globalité-médiation » [9] ; ainsi, pour lui, la notion de faisceau rend nécessaire que la mathématique contemporaine se situe dans une triplicité (celle-là même que Peirce pratique comme « tiercéité ») sans la réduire à une dualité comme celle mise en œuvre dans la philosophie analytique. D’où qu’une philosophie se voulant à hauteur des mathématiques contemporaines ainsi faisceautisées sera dite synthétique.

 

La référence philosophique à Peirce opère ainsi de manière originale : il s’agit pour Zalamea de le disputer à une certaine philosophie analytique qui aime s’y référer.

Ne connaissant de Peirce qu’une certaine vulgate, j’aurais tendance à traduire la triplicité éidal/quiddital/archéal ainsi :

o   l’éidal désigne le formalisé (s’il est vrai que eidos renvoie aussi bien à la notion d’idée qu’à celle de forme [o]) ;

o   le quiddital désigne l’étant ;

o   l’archéal désigne le constituant,

si bien que cette tridification serait une variante de la triplicité lacanienne symbolique, réel et imaginaire (où l’imaginaire constituerait la dimension constituante du rapport symbolisant une réalité).

Mais je me doute du caractère approximatif de cette grille de lecture…

 

En résumé, Zalamea soutient (réduplication oblige !)

-       qu’une philosophie des mathématiques contemporaines doit être une philosophie contemporaine des mathématiques (tout comme Adorno soutenait qu’une philosophie de la nouvelle musique devait être une nouvelle philosophie de la musique)

-       et corrélativement qu’une philosophie de mathématiques faisceautisées doit être une philosophie déployant son discours sous le paradigme des faisceaux c’est-à-dire abordant les subcontraires de manière pragmaticiste, triadique et synthétique.

 

 

 

Si ce résumé n’est pas trop partial et partiel, il me conduit alors à poser deux questions :

1)     Qu’en est-il du parallèle initialement fait entre faisceaux contemporains et groupes modernes ? En quel sens la méthode philosophique mise en œuvre à propos des faisceaux aurait-elle pu précédemment valoir à propos des groupes ? Ainsi une philosophie des groupes, qui se disposerait à hauteur de son objet (le génitif initialement objectif – philosophie s’appliquant aux groupes – devenant subjectif – la notion de groupe s’appliquant à la philosophie), a-t-elle jamais existé ? Faut-il la chercher, comme le suggère Benoît Timmermans, dans la philosophie du premier romantisme allemand ?

2)     Qu’en est-il du parallèle fait entre rupture mathématique portée par la notion de groupe et rupture mathématique portée par la notion de faisceau ? Si, dans ces deux cas, une philosophie sérieuse doit bien se déployer à l’aune des objets dont elle veut saisir la nouveauté, l’homologie des ruptures proprement mathématiques n’est-elle pas à relativiser ?

La première question est d’ordre philosophique – je la laisserai ici à d’autres examens (la réévaluation de la grande philosophie romantique allemande est un des axes prolongés de travail du séminaire mamuphi et nous aurons donc d’autres occasions, je l’espère, d’y revenir) ; la seconde est d’ordre mathématique et c’est sur elle que je voudrais maintenant enchaîner.

 

Pour le dire simplement, quitte ce faisant à risquer une trop grande naïveté (mais le courage propre de mamuphi n’est-il pas d’oser naïvement jeter les dés entre nous ?), si la notion de groupe constitue bien un déplacement mathématique radical, la notion de faisceau ne constituerait-elle pas plutôt une extension mathématique si bien que, si nos deux notions partagent bien le fait d’être toutes deux des révolutions, elles diffèreraient cependant en ce que la première est une révolution qui tend à abandonner voire détruire l’ancien monde classique (de l’algèbre en l’occurrence) quand la seconde serait une révolution qui étend et par là prolonge ?

Autrement dit, si la révolution galoisienne des groupes a signé l’entrée dans des mathématiques modernes qui pivotaient radicalement par rapport aux mathématiques classiques (disons pour Galois par rapport à l’algèbre de Lagrange), la révolution grothendickienne des faisceaux se présenterait plutôt comme une prolongation étendue des mathématiques modernes (comme en témoigne sa « Longue marche à travers la théorie de Galois » là où il paraît bien difficile d’imaginer que Galois ait pu présenter son travail comme une longue marche à travers l’algèbre de Lagrange [p]). Dans ce cas, les mathématiques dites contemporaines devraient être vues comme une nouvelle étape des mathématiques modernes et non comme la nouvelle version des mathématiques avancées qui leur succèdent.

 

 

On aurait donc :

 

 

car on aurait : contemporain = moderne d’aujourd’hui

 

On peut en effet concevoir la notion de faisceau comme l’extension contemporaine de notions modernes et, plus généralement, concevoir que d’autres traits essentiels des mathématiques contemporaines (géométrisation contemporaine succédant à l’algébrisation moderne, logique contemporaine remise sur pieds mathématiques…) constituent tout de même des extensions de problématiques modernes plutôt que des tournants délaissant ou détruisant les inventions modernes comme celles-ci ont pu le faire pour les inventions classiques (voir les reconstructions de part en part du calcul différentiel, de l’algèbre polynomiale, de la géométrie héritée d’Euclide, de l’arithmétique « rationnelle », etc.).

 

 

Ainsi, sans aucunement récuser les nouveautés contemporaines dont traite savamment et encyclopédiquement Zalamea, ne pourrait-on les concevoir comme constituant une nouvelle séquence de la modernité mathématique plutôt que comme séquence déposant les mathématiques modernes comme celles-ci ont pu effectivement déposer les mathématiques classiques ?

 

Adopter cette manière de voir implique alors de diviser la séquence moderne qui, pour Zalamea, s’étend sur un siècle (1850-1950) et d’y distinguer deux séquences :

1)     une séquence de constitution et de généralisation – nommons-la Modernité-I [M-I] – qui s’organise autour de Galois, Riemann [q] et Cantor ;

2)     une séquence d’axiomatisation [r] et de formalisation – nommons-la Modernité-II [M-II] – qui s’organise autour de Artin, Hilbert et Gödel [s] - je dissocie donc ce que Zalamea unifie selon la succession « Gazlois, Riemann, Poincaré et Hilbert » [10] ;

en sorte que les mathématiques contemporaines de l’après-guerre s’avèrent alors constituer un troisième moment qu’on nommera Modernité-III [MIII], moment d’extensions qui s’organise autour cette fois de Grothendieck, Langlands et Cohen.

 

Reste alors, comme on va y revenir, de savoir si les mathématiques ne seraient pas engagées, depuis le tournant du siècle qui aussi celui d’un millénaire, dans une quatrième moment M-IV dont nous aurions d’autant moins l’intelligence surplombante que nous n’en serions qu’à son entame.

 

Au total, on aurait donc :

 

On aurait ainsi affaire à deux logiques nominatives :

-       les mathématiques contemporaines succèdent aux mathématiques modernes comme celles-ci ont succédé aux mathématiques classiques ;

-       les mathématiques contemporaines constituent le troisième moment de mathématiques modernes dont le destin dynamique s’avère de très long cours.

 

L’enjeu de ce qui peut se présenter indument comme une simple querelle terminologique me semble pourtant massif. En effet, il en va en cette affaire moins des choses ainsi nommées que de leurs rapports : en effet, la question ne porte pas tant sur ce que sont les mathématiques modernes ou contemporaines que sur leur rapport.

Parler de tels rapports, c’est aussi bien traiter aujourd’hui de la question : que continuer, et comment continuer ? Continuer les voies ouvertes par l’humanité depuis 1848 dans les différents domaines de la pensée sous le signe général d’une très longue marche moderne, ou dépasser la modernité pour un contemporanéisme de plus en plus constitué négativement et sans autre affirmation véritable que d’ordre nihiliste (« plutôt que ne rien faire avant la fin du monde, faisons au moins quelque rien susceptible d’enjoliver notre fin »).

Je dramatise sans doute à l’excès le carrefour indiqué aux fins d’indiquer que ses enjeux sont réels et nullement de nature nominaliste.

 

 

Pour revenir à notre interrogation sur les mathématiques contemporaines, ne peut-on donc voir toute une série de leurs inventions capitales comme des extensions modernes, comme des prolongations par élargissements ?

 

Parcourons pour cela très rapidement trois marqueurs des mathématiques contemporaines.

 

1)     Les faisceaux

Ne peut-on, somme toute, considérer un faisceau comme « un objet mathématique qui se déforme de manière continue lorsque l’on parcourt les points d’un certain espace de paramètres : un paramètre qui peut être le temps, ou n’importe quoi d’autre » (Francis Borceux [t])

Le faisceau devient ainsi vu comme une sorte d’extension de la notion d’espace topologique par adjonction d’un paramètre.

 

2)     La géométrisation

Si les mathématiques contemporaines mettent bien en œuvre un tournant géométrique de la pensée, ne peut-on trouver les prémisses de ce tournant dès la théorie de Galois s’il est vrai que celle-ci repose sur une protogéométrie première, donnant sens aux symétries [u], éléments du groupe de Galois ?

En ce sens, les mathématiques contemporaines viennent clarifier et systématiser un geste, fondamentalement à l’œuvre dans les mathématiques modernes dès leur constitution.

 

3)     La remise sur ses pieds mathématiques de la logique contemporaine

Si l’on examine enfin la logique mathématique, on constate que la logique contemporaine s’oppose au tournant logiciste et langagier en ce qu’elle ne prétend plus fonder la mathématique mais, tout au contraire, assume de reposer sur une base mathématique ; ainsi, « la supposée reconstruction logique des mathématiques – mille fois étudiée dans les textes analytiques – va clairement à l’encontre de ce que la logique mathématique a découvert dans la période 1950-2000. » [11] et « La logique mathématique contemporaine en est venue à démontrer comment une protogéométrie précède nécessairement une logique. » [12]

Mais ce point n’est-il pas, là encore, non pas exactement un tournant mathématique mais plutôt une prolongation étendue d’orientations modernes s’il est vrai par exemple que, dans la théorie des ensembles, ce sont bien les décisions d’existence qui imposent leurs conséquences logiques et nullement l’inverse : on déduit les propriétés qui sont susceptibles de valider logiquement les existences mathématiques préalablement décidées.

D’ailleurs, l’intégration de cette « géométrie de la logique » à un développement périodisé prenant racine dans la modernité mathématique est explicitement revendiqué par Jean-Yves Girard selon trois étapes que le livre nous rappelle : « 1900-1930, le temps des illusions ; 1930-1970, le temps des codages ; 1970-2000 : le temps des catégories » [13].

 

Dans ces trois exemples, la nouveauté contemporaine semble donc pouvoir s’interpréter comme prolongement du moderne par extension plutôt que comme opposition radicale au moderne, ce moderne qui, lui, s’est bien constitué en opposition marquée au classique.

Rappelons au demeurant qu’une extension est tout autant révolutionnaire qu’une destruction suivie d’une reconstruction ou qu’un abandon suivi d’un déplacement s’il est vrai qu’une révolution est un bouleversement radical d’ensemble et que l’adjonction d’une nouvelle dimension répond assez exactement à ce double critère. [v]

 

Zalamea, il est vrai, répond en un sens à ces questions en examinant dans le tableau suivant les « quelques traits qui aident à démarquer mathématique moderne (1830-1950) et mathématique contemporaine (1950-aujourd’hui) » [14] :

 

Sur les dix traits qu’il recense, cinq - la moitié donc – distinguent la mathématique contemporaine. Les voici :

-       impureté structurelle (l’arithmétique via le continu)

-       géométrisation ubiquitaire (noyaux géométriques archéaux)

-       schématisation (caractérisations catégoriques)

-       fluxion et déformation (revers des propriétés usuelles)

-       réflexivité (formes complexes d’auto-référence)

 

M’approprier ces traits distinctifs, donc aussi bien la mathématique qui la constitue et la philosophie qui la soutend, relève d’un travail d’une tout autre haleine que celui que j’ai pu jusqu’à présent mener sur ce stimulant ouvrage mais, malgré cela, quelques remarques sur deux de ces cinq derniers traits.

 

Impureté structurelle

Ne peut-on voir l’impureté des mathématiques contemporaines comme dressées contre une pureté privilégiée seulement en M-II en sorte que l’impureté de M-III se présente en partie aussi comme un retour à l’impureté native de M-I, le caractère structurel de l’impureté en M-III représentant alors précisément la figure extensive d’une impureté moderne ?

Par exemple, comme Pierre Cartier nous le rappelle, en 1983 la démonstration par Charles Hermite de la transcendance de e a rencontré des objections en raison de l’impureté de son raisonnement mobilisant des méthodes transcendantes pour un résultat arithmétique.

 

Géométrisation ubiquitaire

J’ai indiqué que la théorie de Galois peut déjà être conçue comme adossé à une protogéométrie si bien que la nouveauté contemporaine se concentrerait plutôt sur la qualification « ubiquitaire » de cette géométrisation moderne.

 

Je m’arrête là, faute de temps (temps de travail sur cet ouvrage, temps aujourd’hui d’exposition) mais ne peut-on envisager que ces cinq traits distinctifs n’invalideraient pas mon orientation générale (le contemporain comme extension du moderne) mais caractériseraient plutôt le troisième moment moderne – M-III – voire préfigureraient l’éventuel quatrième moment – M-IV – dont les incertitudes actuelles seraient le symptôme précurseur ?

 

 

Dernière remarque globale.

On le pressent : évaluer les réponses philosophiques que ce beau livre apporte impliquerait alors de discuter en détail ce que « philosophie des mathématiques » veut exactement dire en cette circonstance – quel rapport, en particulier, avec l’épistémologie ? - et mesurer le déplacement philosophique opéré par rapport au travail de référence de Lautman avec la décision d’adopter la pragmatique de Peirce en référence princeps.

Ici une suggestion : ce vaste travail ne se déploie-t-il pas en premier lieu comme intellectualité mathématique plutôt qu’en philosophie de la mathématique, autant dire comme tentative de ressaisir la pensée mathématique en intériorité en sorte à la fois de la soutenir, de la prolonger et de lui assurer le rayonnement maximal pour les autres domaines de la pensée (là où une philosophie conditionnée par les mathématiques contemporaines – je pense bien sûr exemplairement à celle d’Alain Badiou – se déploie plus en extériorité conceptuelle à des fins plus proprement philosophiques [w]) ?

Ceci expliquerait alors en bonne part le caractère sauvagement foisonnant du vocabulaire mobilisé par le mathématicien pensif pour mettre des mots sur sa réflexivité.

 

Le séminaire mamuphi est un excellent lieu pour poursuivre collectivement (une journée complète l’année prochaine ?) ce premier examen, d’autant plus important que les mathématiques contemporaines me semblent constituer aujourd’hui une base solide pour tous ceux qui s’interrogent sur les modernités.

En effet, aujourd’hui, au moment même où, dans tous les domaines (artistiques, politiques, scientifiques…) se pose l’angoissante question : faut-il continuer ou faut-il abandonner les pas acquis pour se perdre dans une sombre fuite en avant, il me semble que la voie suivie par les mathématiques a une valeur exemplaire et que cette voie, précisément, nous rappelle que la modernité (en un sens à repréciser) est toujours en cours, selon une modalité contemporaine qui peut alors s’analyser comme la difficulté du passage de sa troisième étape à sa quatrième étape, nouvelle étape dont les forces vives nous sont encore inconnues mais qui ne pourront s’affirmer, contre toute fuite nihiliste en avant, que dans de nouvelles extensions des affirmations antérieures.

 

***

 

Références