How to theorize
music today in the light of mathematics?
A musician’s point
of view
“Gazette des mathématiciens” [1], n°119, January 2009 [2]
François Nicolas [3]
I. Mathematician manner of
theorizing the music 2
II. Musicologist manner of theorizing the music 5
III. Musician manner of theorizing the music 7
On the whole… 8
“Despite all the experience that I could
have acquired in Music,
as I had practiced it for quite a long time,
it’s only with the help of Mathematics that
I have been able to untangle my ideas,
and that light made me aware of the
comparative darkness in which I was before.”
Rameau (1722)
If the
relationships between mathematics and music can’t be limited to their
theoretical dimension – I had the opportunity, during the last annual day of
SMF [4]
“Mathematics and Music” (June 21st, 2008) [5], to suggest that music and mathematics
would gain a lot by referring themselves to the making of (music from mathematics /
mathematics from music) -, it is however obvious, since the meeting
Euler-Rameau in 1752 [6],
that theorizing music in the light of mathematics is still the most productive
approach.
It is clear
that two hundred and fifty years after this meeting, the ways of implementing
such a type of theorization have significantly changed.
One would
like to clarify the new theoretical configuration reached nowadays, at this
beginning of XXI° century, by the ten years experience [7] which has been deployed under the
denomination “mamuphi” (for mathematics-music-philosophy) [8] which includes a seminar
(Ens-Ircam-CNRS), a school (of mathematics for musicians), and various meetings
or publications [9].
The mamuphi nebula gives us a better analysis
of the various ways to theorize music today in the light of mathematics and to
choose the best mathematical tools for that. In mamuphi, these tools converge: they are
primarily those of the algebraic geometry as redrawn by Grothendieck [10], and more specifically those of his
topos theory [11].
Thus mathematicians, musicologists and musicians converge in mamuphi to privilege this toposic
approach [12];
however, as one will see it, they diverge from each other about the ways of
implementation.
Precise
details
—
To theorize
the music can be done many manners: there are acoustical, psychological,
economical, sociological, ethnological, psychoanalytical, but also philosophical,
epistemological,
etc, theorizations of the music as there are mathematical, musicological and
musical one. Only
these three last methods are active in mamuphi.
—
If mamuphi registers philosophy in its
workspace, it is not primarily for possible philosophical theorizations of the
music - such, for example, that which Adorno have produced -; it is rather the
following conviction: one can theorize the music in the light of mathematics
only in the shade of philosophy (more precisely: in the shade of a given philosophy, suitable for the
followed orientation). This shade of philosophy is due to the fact that what
“theorizing” means does not go from oneself: theorizing does not have a
univocal meaning but depends not only on what is to be theorized, but very as much of which theorizes (say: of its “subject” as
much as its “object”). It is at the precise point where these various designs
from theoretical should be articulated - these “theoricities” - that philosophy
will play its part.
In this
article, one will leave side this philosophical aspect of mamuphi work.
mamuphi confronts three different manners
to theorizing the music (in the light of mathematics and in the shade of
philosophy): a mathematician manner, a musicological manner and a musician manner.
I. Mathematician manner of theorizing the music
This first
manner take again, under the contemporary mathematical conditions, the emblem
of the great Euler. Today, the work of Guerino Mazzola [13] prolongs this mathematical tradition.
Quite
naturally, the musician will find in this Mazzola’s work characteristics
already present in the Euler’s theory of the music. [14]
Theory of a theory
A
mathematical theory of the music always leaves a preexistent theory of the
music, that this theory (which is used as precondition to the mathematician) be
of musical nature (as at the time of Euler) or rather of musicological nature
(like today [15]
for Mazzola). Indeed a mathematician cannot build his theory directly starting
from musical scores (even if he can very well read these scores, the
mathematician will hardly plan to propose a new idea of them) but starting from
preexistent analyses of these scores, therefore from preformed musical theories
which will be used as a basis for its own work.
One can
draw the scaffolding of the theories thus [16]:
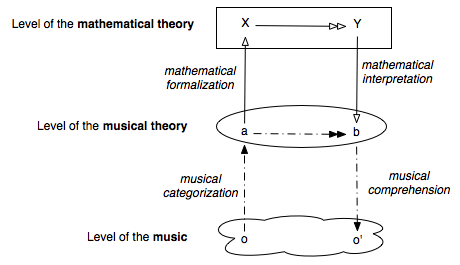
For
example, the Mazzola’s theory undertake, in the course of its vast project, to
formalize:
—
the
theory of the counterpoint by Johann Joseph Fux (XVIII° century),
—
the theory
of the tonal harmony by Hugo Riemann (XIX° century),
—
the
analysis of the Hammerklavier sonata (Beethoven) by two musicologists Ratz & Uhde (XX° century),
—
the
analysis of Structures I.a (Boulez) by Giorgi Ligeti.
To theorize mathematically, it is to formalize, and thus
to deform
To
mathematically theorize an existing musical theory, it is to formalize it
according to own mathematical requirements. This formalization, not being
neither a translation nor a simple transposition [17], thus implies a deformation; it requires
a rehandling of the original theory so that the categories common to both
theoretical faces will have, at the end, very shifted significances.
One can
realize it in the eulerian design of consonance/dissonance relationship [18]. One finds this point at Mazzola, for
example in his formalization of “cadenzas” and of “modulations”: between its
mathematical concepts (of cadenza and of modulation) and the homonymous musical
concepts, the relations will be of intersection rather than of recovery. Let us
explain that.
For its own
needs, Mazzola retains musical modulation only two properties:
—
the
existence of harmonic sequences able to affirm a particular tonality (those
which will articulate a tonal cadenza: for example II-V-I);
—
the
existence of harmonic sequences which are common to two close tonalities (it
acts here to use enharmonic chords, carrying an tonal ambiguity: for example
II-I-IV in major C could be reinterpreted like VI-V-I in major F).
But while
thus proceeding,
—
mathematical
formalization remains indifferent to the order of the harmonic sequences: she
will consider, for example, that sequence VI→II→V→I (perfect cadenza) and
sequence I→II→V→VI (broken cadenza) are mathematically equivalent in the same
unit not ordered {I, II, V, VI}; this manner of seeing will astonish the
musician…
—
In the
same way, mathematical formalization will consider that its “cadenza” {II-V} is
equivalent to its “cadenza” {VII} since this last chord (B-D-F in major C),
which can appear only in this tonality, is alone (among the other chords) to
affirm major C. Again here, the musician will not recognize his music, his
tonalities and his modulations: if, for the musician, sequence II→V is the
gesture of a musical cadenza, on the other hand the simple statement of VII
does not hold place of it since, quite to the contrary, this chord constitutes
the prototype of the polymorphic pivot-chord [19], which is common to many tonalities.
In short,
the musician does not recognize exactly his cadenzas and his modulations in the
homonymous concepts of Mazzola, just as it could not recognize his own harmonic
functions in eulerian formalization of the musical pleasure.
This torsion
concerns a structural law; it does not come from one mathematician lazes or
incompetence: cohesion of the musician experiment and coherence of mathematical
formalization, musical logic and mathematical logic make clearly two. They can approach, enter in
resonance, but they could not amalgamate, nor to even overlap. [20]
Let us give
another example in the way in which the mathematical theorization tends to
deform the musical neighborhoods that it undertakes to formalize.
To test its
mathematical formalization of a musicological theory (by Ratz & Uhde) of
the sonata Hammerklavier (Beethoven), G. Mazzola wonders whether it is possible to find an
musical equivalent with a mathematical formula such as B, formula deductible
(within the framework of its mathematical theory) from the formula A (which
formalizes the sonata as theorized by the musicologists).
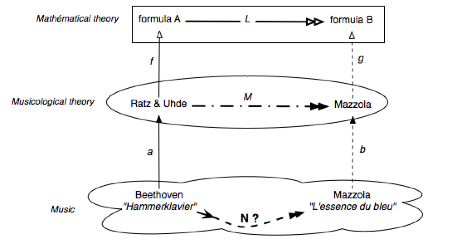
To carry
out that, Mazzola composes a piece for piano (L’essence du bleu) whose musical analysis (arrow b), carried out according to the same
musicological principles that for the sonata of Beethoven (arrow a), then mathematically formalized
(arrow g)
according to the same logic as that which was used for the analysis of the
Beethoven sonata (arrow ƒ), leads well to a related formalization B (arrows L) with starting formalization A.
It is
understood that this device can ensure that there exists, in the theory of Ratz
& Uhde, an arrow M such as the top rectangle commutates (i.e. such as g°M =
L°f) since the new piece of music (L’essence du bleu) precisely was made up so that its
analysis is quite related (by M) with the analysis (by Ratz & Uhde) of the Beethoven’s sonata.
But the
musician will address here to the mathematician an additional question: does
there exist also a kind of arrow N - an arrow which is specifically musical
(and either musicological or mathematical) - such as the rectangle of bottom
(and thus also the complete rectangle) commutates i.e. such as b°N =M°a (and
g°b°N = L°f°a)? In other words, would this theoretical construction induce a
bringing together of nature specifically musical between Hammerklavier and L’essence du bleu?
For the
musician - who is the only one with being able to come to a conclusion about
the properly musical existence of such a relation [21] -, such an “arrow” N does not exist in
this precise case: to examine the two partitions (it is not the place, here, to
do that…), it proves indeed that there is hardly musical relation between the
sonata of Beethoven and the work composed ad hoc by Mazzola, which will not
surprise us: it is not because a certain kind of musicological analysis can
bring closer (arrow M) the analytical structures of two musical works that this
is enough to musically connect these two works (just as two buildings could not
be architecturally related as significant spaces because their plans would
connect the same row of rooms or because one could count the same number of
columns on their frontages…).
This raises
how much such a mathematical theorization deforms the musical world: by
founding formal neighborhoods which do not have musical counterpart, it brings
closer musical objects remaining for the musician extremely distant, just as
contrary it puts distant and separates what for the musician constitutes a
neighborhood (see the families of harmonies built by Euler on the basis of his
scale of the softness: they separate harmonies musically closed and bring
closer musically distant harmonies).
Let us
specify once again. This deformation of musical topology by mathematical
formalization is not due to a negligence of the mathematician. It is an effect
of structure, which is due to the point legitimating the logico-mathematical
construction of a “model theory”: mathematics seizes the field (which it will
undertake to formalize) as discrete space of objects (they are their own
neighborhood). Mathematical formalization will be thus formalization of the
objects (here musical) but by no means of musical relation between these objects,
relations which are voluntarily ignored [22].
The purpose of this formalization will be to build a new (theoretical) type of
space where the new (mathematical) objects will be connected by deductive
relationship, between musical field and mathematical theory being done by
formalization and interpretation of the only (musical and mathematical) objects
but by no means of their respective relationships.
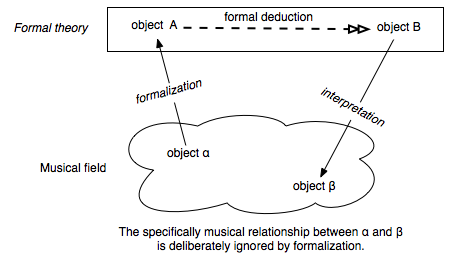
Technically
known as, the theorization in question will thus not be functorial: formalization and interpretation
will not be “functors” between two categories. [23]
Thus, if
the specific interest of any formalization precisely holds with the contrasted
relationship between a starting field formally seized like discrete (without immanent relationships)
and a theoretical field where the objects will be connected by formal
deductions, it goes without saying that the musical relationships (that the
musician knows well but that the theory is unaware of) will appear to this
musician as deformed and not reflected by the theoretical construction in
question. It is to say that the musician reserves with regard to such a
mathematical theorization will be inevitable.
A theory coordinating a sheaf of formalizations
To theorize
mathematically the music engages a great diversity of formalizations which the
mathematician will have to coordinate if he wants to build a theory of the
music and not to accumulate a cluster of local operations.
Mazzola
carries out this coordination within the framework which is offered to him by
the grothendieckian topos theory [24].
Euler, of course, did not have such a preexistent framework, and its
theorization of the music was useful to him precisely - inter alia… - to put the unit of mathematics
of its time (then taken in a vast movement of diversification) proof against a
single object (music)…
In both
cases, a mathematical theory of the music is not satisfied to collect disparate
formalizations and to deal with their mathematical unification. It is
understood that such a requirement concerns a specifically mathematical
command, and not musical at all. From where the following point.
A theory serving mathematics rather than music
Such
mathematical theories, which aim at mathematics much more than music and which
are the subjective business of mathematicians (the musician does not worry more
unit of mathematics that the mathematician does worry to bring a new reading of
such or such musical work) could not be of real use for the working musician.
The
musician, craftsman of his art, will thus be interested hardly in these
mathematical theories; quite simply it will not read them: it is not only that
he could be made perplexed by such or such technical detail; it is more
primarily that he does not need such a type of theory, as well in its practice
as in its possible concern of theorizing the music this time as a musician (one
will examine further the specific manner whose musician will be able to seize
mathematics to theorize the music).
A theory producing of new knowledge on the music
This
implies by no means that such a mathematical theory of the music remains vain
for the musician, at least for the pensive musician [25]. For example the formalization of
Mazzola leads to this remarkable result: the theory of the counterpoint by Fux
and the theory of the harmony by Riemann prove narrowly related by this theory
according to the geometry of intervals which them framework, when, however,
these two theories (of Fux and Riemann) remain separated by the chronology
(respectively XVIII° and XIX° centuries) and by the practice of the musicians
(in music, counterpoint and harmony give place to disjoined lessons, without
theoretical unification [26]).
Thus this
mathematical theory reveals structural properties, up to that point unperceived
of the musician and of the musicologist. It is to say that this theory makes it
possible to extend the knowledge on the music even if it does not make it
possible to invent as regards musicians practices.
It is for
this reason that this mathematical type of theory will interest the
musicologists rather than the musicians if it is true that all and sundry are
distinguished as follows: the musicologists constitute themselves around
knowledge in externality on a music conceived like object already there, when
the musicians proceed of knowledge in interiority of a music which they make.
II. Musicologist manner of theorizing the music
The
musicological manner to theorize the music with mathematics will operate
contrary to the mathematician manner: it will leave this time a mathematical
theory which preexists to apply it to such or such musicological question.
One can
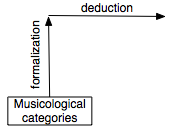
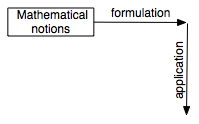
present the contrast of these two dynamics in the following way:
|
Mathematician manner : |
Musicological manner : |
|
|
|
|
It mathematically formalizes musicological categories (which it takes in the existing musicological corpus) to deduce in properly mathematical space from its objects. |
It builds, starting from mathematical concepts (which it takes in the existing mathematical corpus), an original formulation likely to be applied in the specifically musicological space of its categories. |
Altogether,
the musicological manner of theorizing the music with mathematics consists in
building a “mathematical model” for a musicologically given problem: if mathematician
formalization can be conceived like a “mathematization” of the music, the
musicological manner will consist rather of a mathematical “modelization” of
musicology [27].
Thus this last manner privileges, in mathematics, its capacity of calculation
rather than the power of its concepts.
This kind
of musicological theory is committed thus to what is called “a computational
musicology”. In mamuphi, the carrier more succeeded of this orientation is Moreno
Andreatta. [28]
The work of
this musicology is carried out especially in the pure algebra (primarily the
group theory) but an important part is based from now on a modelization in term
of topos. For example, this relates to what the music theory, since David Lewin, calls the
“transformational” approach of the pitchs networks. About what is it?
It is
initially a question of segmenting a score in pitchs groups - say in “chords”…
- connected to each other (transformational network) by musical operations of transposition and inversion in kind to produce a total recovery
of the concerned score. It results from this the constitution of an abstract
space: that of the transformations in the course of the time (transformational
progression) of the
constitutive groups of this network.
This way of
insisting less on the particular nature gathered pitchs that on the structure
of the transformations to which these groups give place organizes a
musicological matter which lends itself then quite naturally to modelization of
a categorical type privileging in the same way the relations between objects.
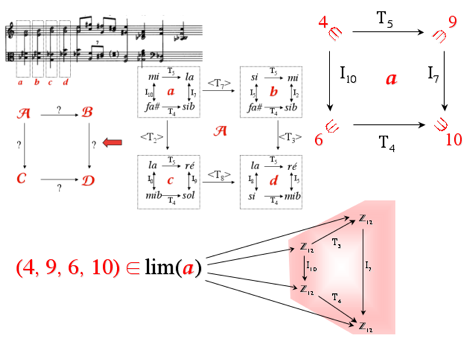
(modelization of a musicological analysis by D.
Lewin of Schoenberg’s op. 11 n°2)
More
precisely, the musicologist, anxious to enumerate and classify these musical
structures (“Klumpenhouwer networks”), will model them in a toposic way (see
the limit for
the last diagram). The result, once implemented by means of computer[29], will be able to release the good
strategies of analysis concerning the networks working in such or such score.
Thus musicological modelization by the topos will lead directly to a
musicological analysis computer-assisted.
Also let us
mention a feed-back effect on mathematics of this musicology: certain
questions, addressed by this formalization to mathematics, will be able to
cause new mathematical problems. It is there what Moreno Andreatta likes to
call a “mathemusical” problem: a musicological problem addressed to mathematics which is
such as its formalization causes new theorems opening then with new
musicological applications. [30]
III. Musician manner of theorizing the music
There
remains a third manner, extremely different, to theorize the music in the light
of mathematics: that of the musician - i.e. of course of the working
musician (there is
not an other type of musician only this one!).
The
musician is distinguished from the two preceding orientations because its
theorization will not aim at producing a “theory” like such: its theorization
will concern rather what Louis Althusser had called a “theoretical practice”,
i.e. an intervention whose stake is not any more the constitution of a
theoretical system, stable and transmissible (“a theory”), but the release of
an idea musician of the music. [31]
For this reason, one will be able to say that the properly musician
theorization is a ideation. [32]
Methodologically,
the recourse to mathematics to theorize the music thus will be carried out
under the sign of what one will call, following Gaston Bachelard, an experimentation of the thought: it will be a
question for the musician at the same time of formalizing and of interpreting
the musical categories and the mathematical concepts in kind to put its discursive
thought proof against mathematical coherence.
Let us give
for that an example, which I will borrow this time from my own work.
To theorize a Music-world
like topos…
Let us
suppose that a pensive musician of today feels the need to theorize how the
music can form a particular world; for such a project it does not miss the good
reasons: for example its desire to be opposed to this new practice, for him
hateful, to put the expression “the musics” instead of the ancestral expression
of the musicians: “music”. [33]
This
musician would like to thus support in thought that there exists well a world
of the music (and not only one area which one can roughly delimit in a general
universe) and only one, and that this world, though internally diversified
(like any world!), remains connected (all that occurs in some place from this
world relates potentially to any other place). In short, the musician would
like to be able to say music what Alain Connes says of mathematics: “there
is only one mathematical world” [34]
and “this mathematical world is connected” [35].
But for
that, how to proceed, how to found such an musician idea of one and only one
musical world?
The
musician, then, will be able to turn to mathematics while saying himself [36]: “the grothendieckian concept of topos
provides a strong contemporary mathematical idea of what is a world; thus let
us put our musician idea of a musical world proof against this mathematical
idea of topos.”
The
musician will then start a theoretical practice which will simultaneously
explore the double sequence of the mathematical concepts and the musical
categories according to the following movement:
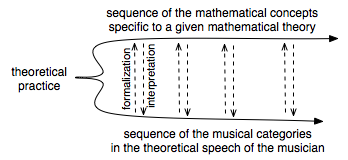
In our
example (how to theorize, in the light of grothendieckian mathematics of topos,
the music like a world?), this experimentation [37] will lead the musician to the following
tasks:
1.
to
formalize a piece of music like a sheaf of executions of its score;
2.
to
formalize the library of the scores of music like a site of its quodlibets;
3.
to
formalize the world of the music like a category of the works extracted from this library;
4.
to
formalize the world of the music like a topos of all these works-sheaves;
5.
to
draw, in the course of work, all useful and relevant conclusions concerning the
musical objects and their relations.
It is
understood that this musician experimentation of the mathematical concepts will
hardly interest the mathematicians, since the effects to wait of such a theorization
will remain intrinsically musical.
This
experimentation will not more interest the musicologists who will not recognize
there the procedures regulating their “objective” production of
knowledge. [38]
One
perceives here a difficulty, specific to confrontations which animate the mamuphi meetings: it does not go from
oneself that the mathematician, musicological and musician theorizations can be
interested between them. Thus the specific challenge of the mamuphi project is precisely to put in
resonance these distinct theoricities, as well objectively as subjectively (one
indicated it besides: it is exactly here that the shade of philosophy is
required).
On the whole…
Let us summarize
our three main trends.
|
|
Mathematization or mathematician formalization |
Modelization or musicological application |
Experimentation or musician theoretical practice |
|
|
|
|
|
|
Stakes of this theorization: |
to make mathematics while widening the power of mathematics and consolidating their unit |
to produce, in objectifying externality, new knowledge on the music |
To deepen, in subjectifying interiority, musical knowledge |
|
Result of this theorization: |
a (mathematical) theory of the music |
a (musicological) theory of the music |
an (musician) idea of the music |
|
The music is: |
an indirect origin (via musicology) |
an indirect target (via musicology) |
a sensible space of thought |
|
Mathematics is: |
a target |
an origin |
a conceptual space of thought |
|
Mathematics concerned takes the form of: |
theories |
formulas & equations |
concepts |
|
The music-mathematics ratios privilege: |
formalizations |
interpretations |
resonances, therefore mathems |
Relations between these three theorizations
Even if
each one understands where the personal preferences of the author (musician) of
this article go, it is however clear that each orientation distinguished here
has its own coherence and that there does not exist position in overhang [39] which would authorize to treat on a
hierarchical basis our three theorizations.
However the
preceding table states that the 3 of our orientations can be deducted, in three
manners, in 2+1.
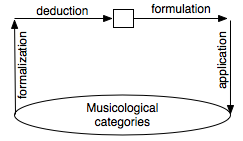
Complementarities
mathematicians/musicologists
Firstly the
mathematician and musicological positions arise in our table like dual and/or
complementary. This complementarity authorizes a new manner, this time mixed, to theorize the music with
mathematics, manner which connects mathematization and application [40] :
Complicities
mathematicians/musicians
Secondly,
one can then notice that mathematician and musician orientations cause narrower
complicities between thoughts in interiority than does not cause a
musicological practice of very technicized modelization, practical privileging
the computing power of mathematics and exteriorizing the “objective” dimension
of the music.
Confrontations musicians/musicologists
Thirdly,
musicological and musicians theoricities meet around the scores since they give
the same direct attention to them. This will maintain between them what one
will call here, with a nice euphemism, a healthy competition…
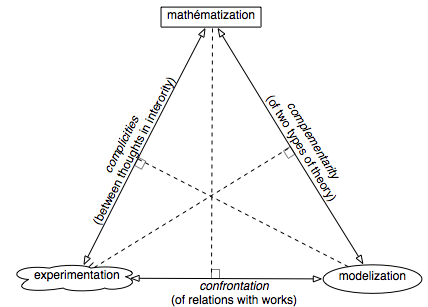
General geometry
The
musician experimentation being “orthogonal” with the complementarity of the
mathematical and musicological theories, - as musicological modelization is
orthogonal with complicities between thoughts in interiority (mathematician and
musician) and as the mathematization is orthogonal with musicians/musicologists
confrontations relating to the scores -, the mamuphi geometry which proceeds of these
relations could be thus drawn:
A counterpoint…
On the
whole, and according to a musical metaphor, the relations between our three
theoricities give to the polyphonic development of mamuphi the pace of a counterpoint.
As the
musicians know it well, they are the dissonances - not the consonances - which
make the music, and these dissonances, at least since Schoenberg, do not need
more to be solved to remain musical.
Thus, the
musician will be able to await the best of these mamuphi dissonances and orthogonalities: it
was here necessary for him to make them clearly hear, so to restore them
according to a mezzo-forte (mf)
rather than a pianissimo (pp)…
––––––––––––
[1] http://smf.emath.fr/Publications/Gazette
[2]
http://smf.emath.fr/Publications/Gazette/2009/119/smf_gazette_119_35-49.pdf
[3] Compositor (École normale supérieure/Ircam)
http://www.entretemps.asso.fr/Nicolas
[4] Société mathématique de France: http://smf.emath.fr
[5] http://smf.emath.fr/VieSociete/JourneeAnnuelle/2008
http://smf.emath.fr/VieSociete/JourneeAnnuelle/2008/Resumes.html
[6] Gazette, July 2008,
n°117 : http://smf.emath.fr/Publications/Gazette/2008/117
http://smf.emath.fr/Publications/Gazette/2008/117/smf_gazette_117_35-47.pdf
[7] The opportunity to start mamuphi was provided by an initiative (at the end of 1999) of
the EMS (European Mathematical Society), which, within the framework of its Diderot forum (http://emis.math.ecnu.edu.cn/etc/diderot4.html), had
chosen “logic” as the issue to be debated in workshops with Ircam.
[8] http://www.entretemps.asso.fr/maths
[9] One will return to the two mamuphi’s inaugural books:
— Mathematics and Music (A Diderot
Mathematical Forum) ; ed. G. Assayag, H.G. Feichtinger, J.F. Rodrigues ;
Springer-Verlag, 2002 - http://www.maa.org/reviews/mathmusic.html
— Penser la musique avec les
mathématiques ?;
éd. G. Assayag, G. Mazzola, F. Nicolas ; Delatour, 2006 -
http://www.ircam.fr/598.html?&tx_ircamboutique_pi1[showUid]=172&cHash=bb50400732
[10] http://www.entretemps.asso.fr/Grothendieck
http://www.grothendieckcircle.org
[11] i.e. the fifth of the twelve “great ideas” which it
releases in “Récoltes et Semailles” (2.8)
http://www.math.jussieu.fr/~leila/grothendieckcircle/RetS.pdf
[12] My own reference books on the matter are Topoi.
The Categorial Analysis of Logic of R.
Goldblatt (North-Holland, 1984) and Sheaves in Geometry and Logic. A First
Introduction to Topos Theory of Saunders Mac
Lane & Ieke Moerdijk (Springer-Verlag, 1992)
[13] See its two reference books:
— The Topos of Music, Birkhaüser, Basel, 2002
— La vérité du beau dans la musique, Delatour, Paris, 2007
[14] Here, one will not present systematically this vast
mathematical theory. It is here only a question of reading this theory as a
musician, i.e. a reading remaining more attached to delimit its matter and to
distinguish its mathematician subjectivity than to explore the properly
mathematical depth of it.
[15] Musicology was invented only during the XIX° century,
under the double influence of the German historicism and French positivism…
[16] Let us specify that this “diagram” (as those which
will follow) only gives one indication of an guiding idea. Thus it has only
illustrative value: the points and arrows which appear here have relationships
only metaphorical with the objects, morphisms and functors of the category
theory.
[17] The philosopher Charles Alunni, co-organiser of the mamuphi seminar, proposes to regard it as one tra(ns)duction.
[18] Gazette, July 2008,
n°117 (op. cit.)
[19] Technically, this chord VII concerns a diminished
seventh. This chord materialized tonal uncertainty by avoiding precisely any
cadential logic. Thus the less (musically) “cadential” chord corresponds, in
mathematical formalization, with the more (mathematically) “cadential” chord…
[20] As one indicated, it is at this place that the shade
of philosophy is necessary.
In
few words, music and mathematics make radically two, without possibility - other that
(neo)-positivist or scientistic - of uniting them. That is due to the
irreducible singularity of the musical work of art. As always, it will go from
there, in this precise place, of sharing between axiomatic:
- either one supports that “there are
works of art” (Hegel), that these works are in art the true subjects; in this
case mathematics could only be unaware of this specificity to seize
work-subjects only by their ontic dimension (that of simple “pieces of music”);
- either one supports that there is
not meaning to distinguish between pieces of music and musical works, that
there is no place in music for a figure of “subject”, for something like a
“musical subject”; in this case mathematics will be able “to seek” to formalize
the music completely as it can legitimately seek to completely formalize the
movement of planets, the reproduction of the ants or the food preferences of
the human animals. But such does a project (to reinstall the music under
supervision of mathematics) constitute for mathematics a real ambition? Without coming to a same
conclusion about the question of works, Euler knew, in all the cases, to avoid
such a covetousness and to respect the autonomy of the world of the music,
without to lose there (quite to the contrary!) the power of thought suitable
for mathematics.
[21] We point out Euler: “In music, as in all the fine
arts in general, it is necessary to be aligned on the opinion of those which
have at the same time an excellent taste and much of judgment. Consequently it
is necessary to hold account only of opinion of people which, having received
nature a delicate ear, perceives with accuracy all that this body transmits to
them, and is able to judge some in a healthy way.” It is thus a question “of consulting the metaphysicians [= here musicians] that this search relates to” (Tentamen…, chap. II)
[22] From this point of view, the particular case where
mathematics formalizes an preexistent “empirical” theory (here musicological
one) - thus a field this time not “discrete” since equipped with internal
relations (of proximity, distance, sequence, etc) and thus with neighbourhoods
non reduced to only one point - constitutes only one alternative since
formalization and interpretation will there continue to relate to only objects,
and by no means to morphisms. The theorization thus considered will not produce
more functor between musicological and mathematical theories: the musicological
theory being used as starting field remains too empirical then to be truly
formalizable in a mathematical category.
[23] A fortiori, one cannot have adjunction between
musical field and mathematical theory. An important aspect of the mamuphi internal debates relates to this precise point…
[24] Let us note its systematic reinterpretation of
categorial morphisms like addresses (familiar with theoretical informatic), x→y being rewrited like x@y..
[25] The musician tends to becoming pensive “when the
music stops” (Th. Reik), the musician finding itself then temporarily vacant
out of musical world. It is the moment when he is naturally led to reflect on
what arrived to him, to charge its musical experiment to encourage itself to
continue its to and from (in/out Music-world).
Like
the mathematicians, the musicians are regularly subjected to nihilist
temptation: the temptation of “What good is it? ”, “in vain” (Nietzsche). That the
abandonment of their cause often takes the form not from a desertion but from a
academization does not withdraw anything with the fact that it is indeed a
subjective resignation.
[26] The unification is carried out only practically, for
example by the school exercise of the choral and of the fugue…
[27] Let us recall that “model” gets busy here contrary to
meaning that this word has in (logico-mathematical) “model theory”. In “model
theory”, the word “model” indicates the original to copy; in “mathematical
modelization”, the same word “model” indicates the reduced model, the model to
be interpreted. For a discussion of the philosophical meaning of this
(neo-positivist) inversion, one will return to the book of A. Badiou: The
Concept of Model, transl. by Zachery Luke
Fraser & Tzuchien Tho (Melbourne: repress, 2007).
[28] Let us indicate that this computational musicology
finds a natural prolongation in a particular seminar, related with mamuphi, which is held in Ircam under the name MaMuX: http://www.ircam.fr/equipes/repmus/mamux
One
will find in the Journal of Mathematics and Music many contributions to this new type
of musicology: http://www.tandf.co.uk/journals/titles/17459737.asp
[29] To see From has Categorical Point of View: K-Nets
ace Limit Denotators (G. Mazzola and
Mr. Andreatta, Prospects of New Music, 44-2, 2006) and, more generally, works of the team Musical
representations in Ircam:
http://recherche.ircam.fr/equipes/repmus
[30] It would thus, in my opinion, be a question rather of
a “mathemusicological” problem…
[31] This musician idea on the music is distinguished, of course, of the musical idea: that which, in the course of the work, takes
the shape of a musical object, for example of a theme.
[32] I call “musical intellectuality” this musician
ideation.
We
thus do not mislead on the theoretical work of Rameau, this pioneer of musical
intellectuality. Its evolution stresses that, since the departure, it was a
question for him of intervening theoretically for the benefit of a certain
(harmonic…) idea of music, badly established at its time; its “theory” was thus
a (theoretical) manner of pleading its cause of “harmonic” musician rather than
melodic one by giving to this “theory” strong bases, rooted in the rationality
(in particular Cartesian) of its time.
[33] Let us say that it is, here, about a concern
specifically musician for the unit of the music. This concern is very
equivalent to the eulerian concern of preserving the unit of mathematics beyond
the beneficial diversity of its practices.
[34] A View of Mathematics:
http://www.alainconnes.org/docs/maths.ps
[35] Les déchiffreurs, p.
14, Belin, 2008
[36] The musician will be thorough with this operation by
the book of Alain Badiou (Logics of Worlds: Being and Event, Volume 2, transl. by A. Toscano; New York: Continuum, 2008)
since this book supports that the philosophical concept of world must be
established today under condition of the mathematical category of topos.
[37] For more details, one will be able to refer to a
first presentation of this work in progress:
http://www.entretemps.asso.fr/Nicolas/2008/Faisceaux.htm
[38] So that a musicologist can be interested in a “idea
musician”, it is necessary for him initially to vitrify it in a “musicological
object” …
[39] Philosophy does not concern more from a Sirius point
of view…
[40] This manner operates very directly in mamuphi: on a side the works of Mazzola, which worry to
informatically implement its theory, stress the computational repercussions of
its mathematical theory and, on another side, musicological work of Andreatta
roots narrowly in the mazzolian theory of the music.