De trois manières de
théoriser la musique avec les mathématiques
(Petit bilan mamuphi 1999-2008)
François Nicolas
Plan
Prélude 3
Théorie/critique/esthétique 3
Trois manières 3
Un troisième moment-mamuphi 4
Petite précision 5
Cadre terminologique 5
Un diagramme général.......................................................................................................... 5
Le spectre de l’adjonction..................................................................................................... 6
Remarque.............................................................................................................................. 7
Et sa reformulation néopositiviste… 7
I. Application (musicologique) 9
Exemple : David Lewin 9
1. Privilégier l’interprétation musicale des mathématiques..................................................... 9
2. Concevoir la théorisation comme une modélisation........................................................... 9
3. Concentrer la formalisation mathématique en une
formulation.......................................... 9
Une interprétation plutôt qu’une formalisation.................................................................... 10
Figure applicative de la commutativité 11
Exemple chez Carl Dahlhaus............................................................................................... 11
Subjectivité à l’œuvre 11
La figure subjective de l’ingénieur...................................................................................... 12
La figure subjective du musicologue................................................................................... 12
Philosophie spontanée 12
Le néopositivisme du musicologue...................................................................................... 12
… matiné de la phénoménologie du musicien..................................................................... 12
Emblème : la music theory 13
II. Mathématisation (mathématicienne) 14
Exemple : Guerino Mazzola 14
1. Privilégier la formalisation mathématique de la musique................................................. 14
2. Pour cela, partir d’une théorie musicale préexistante....................................................... 14
3. La cible : un développement théorique dans les
mathématiques....................................... 14
Au total…........................................................................................................................... 15
Remarque............................................................................................................................ 15
Figure mathématisante de la commutativité 16
Exemple chez Mazzola........................................................................................................ 16
Subjectivité à l’œuvre 16
Philosophie spontanée ? 17
Deux manières symlétriques de théoriser 17
III. Expérimentation (musicienne) 18
Rapport constituant plutôt que constitué 18
Espacement plutôt que rapprochement 18
Musicien plutôt que musicologue 18
Un nouveau sens de ce que « théoriser » veut musicalement
dire 18
Des « faits » constitués plutôt que constituants 18
Trois exemples 19
1. Théorie de l’audition musicale........................................................................................ 19
2. Théorie de l’écoute musicale........................................................................................... 19
3. Formalisation des rapports cinématographiques
musique-paroles-images dans Muriel..... 21
Traits caractéristiques 22
Fiction................................................................................................................................. 22
Mathèmes............................................................................................................................ 22
« Théoriser », en un autre sens du terme….......................................................................... 22
Philosophie......................................................................................................................... 23
Raisonances......................................................................................................................... 23
Au total…........................................................................................................................... 23
Philosophie spontanée 23
Gaston Bachelard ............................................................................................................... 24
Albert Lautman................................................................................................................... 24
Jean Cavaillès...................................................................................................................... 24
Alain Badiou ...................................................................................................................... 24
Postlude 26
Récapitulation 26
3=2+1 !............................................................................................................................... 26
Intersubjectivités ? 26
Annexes 29
Annexe 1 : Le mythe pythagoricien d’une « mathémusique » 29
1. Nœud mathématisation⊗application................................................................................ 29
2. Continuité d’un geste (ou thèse des voisinages
induits).................................................... 30
Remarque 30
3. Complémentarité mathématiques-musique (ou thèse de
l’adjonction).............................. 32
Remarque 33
4. La réduction mythologique de la séparation
mathématiques|musique.............................. 33
Annexe 2 : Mamuphi 35
Petite chronologie mamuphi................................................................................................ 35
Les 32 interventions du séminaire mamuphi durant la période 2005-2007.......................... 35
Notes de fin (références des citations) 36
Prélude
De façon spontanée, le travail mamuphi [1]
s’est focalisé autour de la question suivante : comment théoriser la
musique avec les mathématiques ?
Théorie/critique/esthétique
On peut considérer en effet qu’un « dire la
musique » [2]
se déploie spontanément selon trois dimensions enchevêtrées : une critique évaluatrice des œuvres musicales, une théorie du monde de la musique, une esthétique des rapports de la musique à son époque. Or, le
discours critique se rapporte
spontanément aux autres arts et à la littérature (l’invention de la critique
musicale peut d’ailleurs être attribuée à Diderot), le discours théorique aux sciences (c’est en priorité avec les sciences
que le musicien discute ce que « théoriser » veut dire) et le
discours esthétique à la
philosophie (c’est d’elle que le musicien s’instruit d’un Zeitgeist) [3].
C’est donc à bon titre que le rapport aux mathématiques, constitutif de
l’esprit mamuphi, a orienté le discours
sur la musique vers sa dimension théorique.
Remarquons que la troisième composante de mamuphi – la
philosophie – y intervient en dernière position. Elle n’est donc pas
immédiatement constitutive de son travail mais y joue un rôle qu’on dira subordonné
aux rapports envisagés entre musique et mathématiques : la philosophie
intervient dans mamuphi comme
éclairant à quelles conditions de possibilité tel ou tel type de rapport entre
mathématiques et musique s’avère soutenable.
Au total, on posera donc que la plate-forme constituant la
subjectivité mamuphi - et rendant raison
d’échanges se prolongeant depuis dix ans (1999-2008) par-delà d’importants
différends entre ses participants - tient au projet suivant :
« théoriser
la musique avec les mathématiques
en éclairant les
conditions philosophiques de possibilité d’un tel ‘avec’ ».
Trois manières
Ceci posé, l’histoire de mamuphi permet de clarifier trois manières sensiblement
différentes de théoriser la musique avec les mathématiques, trois manières qui vont s’avérer donner un sens
sensiblement différent aux mêmes mots utilisés par tous : « la musique »,
« les mathématiques », « théoriser », « avec ».
Pour aller ici au plus direct — dans l’esprit bourbakiste
d’un « fascicule de résultats » plutôt que du compte rendu d’une
genèse — je soutiendrai qu’on peut distinguer :
1. Une
manière musicologique de théoriser la
musique avec les mathématiques, manière qui prend la forme d’une application de théories mathématiques existantes à la musique.
Cette application, affaire
d’ingénieur plutôt que de mathématicien, trouve dans le positivisme logique sa
philosophie spontanée et dans la music theory américaine son emblème. Cette manière de théoriser
la musique a des enjeux essentiellement musicologiques : elle vise à
dégager en extériorité objectivante de nouveaux savoirs sur la musique.
2. Une
manière mathématicienne de théoriser la
musique avec les mathématiques, manière qui se matérialise comme formalisation
mathématique de théories musicologiques [4]
existantes et qu’on proposera ici de nommer mathématisation. Cette mathématisation trouve dans le Journal of Mathematics & Music
son emblème [5]. Elle n’a
pas a priori de philosophie spontanée spécifique [6].
Cette manière de théoriser la musique a des enjeux essentiellement mathématiques :
elle vise, à partir d’un examen mathématique de la musique, à dégager de
nouveaux savoirs proprement mathématiques, de nouveaux « objets » ou
champs théoriques mathématiques, bref, à approfondir la puissance ontologique
propre des mathématiques.
3. Une
manière enfin proprement musicienne de
théoriser la musique avec les mathématiques, manière qui prend la forme d’une expérimentation inventant simultanément son modèle et sa
formalisation. Cette expérimentation
trouve sa philosophie spontanée dans une généalogie française (de Bachelard à
Badiou [7]), et son emblème
dans la notion de raisonances [8]
(par commodité d’exposition, je l’illustrerai ici essentiellement de mes
propres travaux [9]).
Cette manière de théoriser la musique a des enjeux proprement musicaux :
elle ne vise ni des savoirs exogènes sur la musique, ni des développements mathématiques propres mais une
meilleure compréhension, en intériorité subjective, de la pensée musicale, disons une meilleure connaissance musicienne, tout particulièrement une meilleure
compréhension musicienne des œuvres musicales [10].
À ce titre, cette manière de procéder s’intègre à ce que j’appelle une intellectualité
musicale [11].
Application musicologique, mathématisation mathématicienne,
expérimentation musicienne, telles sont donc les trois manières de
« théoriser la musique avec les mathématiques » mises au jour par le
travail mamuphi.
Un troisième moment-mamuphi
Ces trois manières composent un faisceau tout à fait
original – chaque manière constitue d’ailleurs une invention de la fin du xx°
siècle — qui configure un nouveau moment-mamuphi – le troisième - après le moment Grec fondateur (VI°-IV° siècles av. J.-C.) et le moment Classique (XVII°-XVIII° : de Descartes à la confrontation
Euler-Rameau-Rousseau).
Petite précision
Il s’agit ici de distinguer trois régimes de consistance théorique. Comme on va le voir, les critères de validation de chaque manière de théoriser la musique ne seront pas les mêmes, sans qu’existe une sorte de méta-disposition théorique qui subsumerait ces trois régimes et permettrait de combiner sans hiatus leurs résultats.
Ceci n’exclut cependant pas que tel ou tel auteur puisse, au fil apparemment d’une même plume, alterner les dispositions. Cette éventuelle pratique ne sera pas ici entendue comme une symbiose ou un mixage (en général consistance A ⊗ consistance B ⇒ inconsistance…) mais plutôt comme une attestation particulière de cette donnée à mon sens bien établie qu’un même individu peut être successivement partie prenante de différents processus subjectifs [12].
On se gardera donc de conclure de cette succession hétérogène à une synthèse homogénéisante…
Cadre terminologique
Fixons d’abord un cadre terminologique de référence,
susceptible d’embrasser la diversité des orientations mamuphi.
Je l’emprunterai à cette partie de la logique mathématique
qui s’appelle « théorie des modèles » et dont on trouvera une
ressaisie philosophique tout à fait éclairante pour notre propos dans le livre
d’Alain Badiou récemment réédité : Le concept de modèle [13].
Un diagramme
général
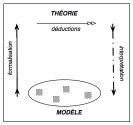
L’idée générale est de mettre en rapport deux domaines de
pensée hétérogènes et disjoints (respectivement nommés « modèle » et
« théorie », correspondant ici à la musique et aux mathématiques)
selon le schème suivant :
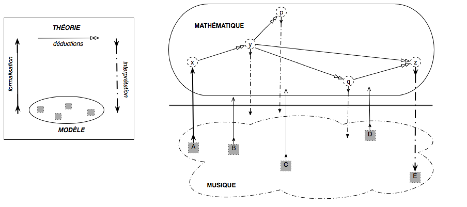
Le modèle (ici la
musique) est constitué d’entités « A », « B »,
« C » et de valeurs de vérité attachées à chacune de ces entités. Il
n’a pas besoin d’être doté de relations entre ces entités, moins encore de relations orientées (de flèches) si
bien que le modèle ne saurait constituer à proprement parler une catégorie, par
défaut de morphismes.
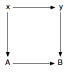
À chaque entité « A » du modèle, on associe, par
une « formalisation », une entité « x » du second domaine
appelé « théorie » (ici les mathématiques). Inversement, à chaque
entité « z » de la théorie, on associe une entité « E » du
modèle par une « interprétation ». À la différence du modèle, le
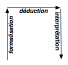
domaine « théorie » est doté de la possibilité d’y déduire ; il
connaît donc des flèches (orientées) du type x→y. À ce titre il est, sous
certaines conditions supplémentaires, susceptible de constituer une catégorie,
voire un topos.
Tout l’intérêt de ce montage expérimental tient alors à la
constitution de diagrammes du type suivant :
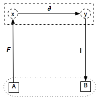
qui vont « relier » A et B via la composition
I°∂°F des trois flèches F, ∂ et I.
Dans notre cas, le domaine musique, pris ici comme modèle, n’est donc pas censé
connaître de déductions musicales (du type A→B), ni même de relations
immanentes propres. Une formalisation mathématisée de la musique va précisément
permettre de déduire et de calculer non pas directement sur les entités musicales
(A, B, C…)
mais sur leurs formalisations x, y, z…
Notons que dans cette problématique, le mot
« modèle » désigne le domaine original (celui du bas dans notre
schématisation), celui qu’il s’agit de copier, celui qui sert de canon à
l’imitation théorique.
Le
spectre de l’adjonction
Le petit diagramme ci-dessus (où A et B sont « reliés »
par I°∂°F) suscite la question suivante : le parcours I°∂°F composé
successivement d’une formalisation F, d’une déduction ∂ et d’une interprétation
I ne pourrait-il servir à définir, cette fois dans le modèle, une flèche AB :
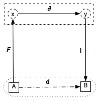
Dans ce cas, le modèle, ainsi muni de morphismes, pourrait être
considéré comme une catégorie – à l’égal de la théorie — et les flèches F et I
pourraient être considérées comme représentant des foncteurs entre ces deux
catégories. Auquel cas se poserait la question suivante : ces foncteurs F
et I (sur les deux catégories « modèle » et « théorie »)
seraient-ils adjoints ?
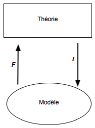
Il semble bien en effet que F puisse alors être adjoint à gauche de
I (et I adjoint à droite de F) puisque ∀A
et ∀y, à toute flèche F(A)y correspondrait biunivoquement
une flèche AI(y) : précisément la
flèche « d » construite ainsi d = I°∂°F !
Mais tout le point est alors de savoir si une telle flèche
« d », ainsi construite apparemment « dans » le modèle, lui
appartient bien, c’est-à-dire si cette nouvelle flèche « d » a bien
une signification endogène au modèle ou si
elle n’a de sens qu’extrinsèque ! Dans notre cas, la question
devient : les flèches ainsi construites sur les entités musicales via la
théorisation mathématique sont-elles ipso facto musicales, ont-elles une réalité musicale ou restent-elles musicalement arbitraires ? Par exemple, ces flèches
« d » obtenues à partir de déductions mathématiques
correspondent-elles à des variations ou des développements proprement musicaux ? Si B = d(A) au sens
où B = I°∂°F(A), ceci veut-il dire que B varie ou développe A au sens musical du terme ? Rien n’est moins sûr !
Comme on va le voir, cette question de l’adjonction entre formalisation et interprétation se trouve au cœur des débats mamuphi.
Remarque
Donner ainsi le modèle, sans « morphismes » internes, comme une pure collection d’entités A, B, C… dont l’existence est attestable (valeur de vérité attachée), suggère que ces entités pourraient constituer des « faits », point de départ du travail théorique. Selon cette acception, la « philosophie spontanée » de cette diagrammatisation de l’activité théorique est le positivisme pour qui, en effet, les rapports entre les choses mêmes sont inaccessibles en sorte qu’on ne puisse viser que des lois entre phénomènes (entendus comme conséquences accessibles de causes restant scientifiquement inaccessibles). Cette vision des choses, procédant d’une présentation formelle de la « théorie des modèles », va conduire à une reformulation néopositiviste de notre schéma de base..
Et sa reformulation néopositiviste…
Sous l’influence du néopositivisme, le champ théorique va se
trouver en effet renommé « modèle » (en entendant cette fois le terme
« modèle » non plus comme original ou canon mais comme modèle réduit
ou maquette). D’où que, dans cette acception néopositiviste, le travail de
théorisation soit alors renommé « modélisation » (construction d’une
maquette théorique).
Cette manière de nommer les choses est aujourd’hui d’usage
courant dans les dites « sciences humaines et sociales » : en
économie (un « modèle théorique » sera une mise en équation de
relations entre données de la Comptabilité Nationale) mais également en
anthropologie depuis Claude Lévi-Strauss [14].
Ce différend n’est pas que terminologique [15].
Il touche directement à la compréhension de ce que théoriser et formaliser veut dire.
·
L’interprétation positiviste (A. Comte, xix°)
de notre schème tient à l’idée philosophique que le domaine du bas (dans notre
diagramme) serait constitué par des « faits » (nos entités
« A », « B », etc.), « données » empiriques tirées
de la « pratique », qu’il s’agirait ensuite (dans un second temps) de
théoriser, c’est-à-dire de formaliser en « lois » (ici de
« modéliser »). On a ici la première transformation terminologique
suivante :
↪≡
·
La thématisation néopositiviste (Cercle de Vienne, xx°)
accuse ce parti pris en projetant la conception positiviste précédente dans
l’espace langagier et les catégories du langage : en renommant en particulier
l’articulation des deux domaines selon la dualité syntaxe/sémantique :
≡ ≡
si bien que dégager les bonnes « lois » rendant compte de « faits » avérés passe ici par la constitution d’un « langage » adéquat…
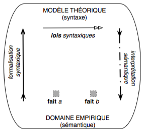
D’où, au total, la thématisation (néo)positiviste suivante
de notre précédent diagramme :
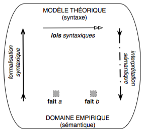
La « modélisation » devient alors une manière de
formaliser en « langage mathématique » les « lois » propres
aux « faits empiriquement constatables », de doter le domaine
empirique d’un langage formel apte aux déductions syntaxiques.
On retrouve ce même schème dans les différentes dualités
suivantes :
(Claude Lévi-Strauss)
(économie)
= (Rudolf Carnap [16])
*
Restons-en là pour l’instant, mais cette ligne de partage
sur la notion même de modèle (modèle à
imiter, ou « modèle réduit ») va se retrouver au fil du travail mamuphi.
Pour la suite de ce texte, j’adopterai systématiquement
l’acception première (celle de la logique mathématique, qui peut
philosophiquement être dite matérialiste [17])
du mot modèle et mon vocabulaire sera
donc systématiquement celui du premier diagramme.
|
Position matérialiste (le modèle est à copier) |
Position néopositiviste (le modèle est une copie) |
|
|
|
Sur cette base formelle, les trois manières mamuphi de concevoir comment théoriser la musique avec les mathématiques vont se distinguer de la manière
suivante :
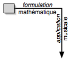
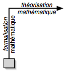
1. une
première manière (« application »), prenant la mathématique pour
point de départ et la musique pour cible, va privilégier les flèches
descendantes (de haut en bas) de notre schéma fondamental : les interprétations (de la mathématique dans la musique) ;
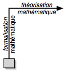
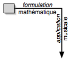
2. à
l’inverse, une seconde manière (« mathématisation »), prenant cette
fois la musique pour point de départ et la mathématique pour cible, va
privilégier les flèches ascendantes (de bas en haut) : la formalisation (de la musique dans la mathématique) ;
3. enfin
une troisième manière (« expérimentation ») va saisir simultanément
les flèches des deux sens dans la constitution d’un espace autonome de pensée,
dialectiquement disposé.
Voyons cela plus en détail, en prenant à chaque fois un
travail théorique singulier comme exemple-type : successivement celui de
David Lewin, celui de Guerino Mazzola et le mien.
Il ne s’agira pas là d’examiner systématiquement ces diverses théories mais d’en proposer une lecture symptomale, ajustée à l’objectif propre de ce travail : objectiver différentes orientations subjectives en matière de théorie musicale.
I. Application (musicologique)
Exemple : David Lewin
La figure il me semble la plus aboutie de
« l’application musicologique » se trouve dans le travail de David
Lewin. [18]
On se référera pour ce faire à deux écrits centraux de sa
vaste production [19] :
·
Music
Theory, Phenomenology, and Modes of Perception (1986) [Lewin-a]
·
Generalized
Musical Intervals and Transformations (1987) [Lewin-b]
Rehaussons pour ce faire trois traits significatifs de sa
manière de théoriser la musique [20].
1.
Privilégier l’interprétation musicale des mathématiques
L’entreprise théorique de Lewin privilégie les flèches interprétatives (allant des mathématiques vers la musique) dès
l’entame de son ouvrage central [Lewin-b] puisque son premier chapitre est constitué de « mathematical preliminaries »
[21]
que Lewin va ensuite « appliquer » à ses cibles musicologiques propres.
Point subjectivement très caractéristique : Lewin va
aussitôt choisir de renommer les concepts mathématiques utilisés pour mieux
ajuster son vocabulaire à ses fins musicologiques propres :
A
mathematician would begin saying, “Let S be a set.” Unfortunately, music theory
today has expropriated the word “set” to denote special music-theoretical
things in a few special contexts. So I shall avoid the word here. Instead I
shall speak of a “family” or a “collection” of objects or members. When I do
so, I mean just what mathematician mean by a “set”. For present purposes, it
will be safe to leave the sense of that concept to the reader’s intuition.
Comme dans toute démarche de type applicatif, Lewin ne va
pas s’intéresser ici [22]
aux procédures de pensée propres aux mathématiques, en particulier à leurs
démonstrations et à leurs stratégies conjecturales, pas même à la cohérence de
leurs concepts propres. Il ne retient de la mathématique que ses
résultats ; plus exactement : ce qui de ces « résultats »
est susceptible de s’appliquer aux problèmes musicologiques qu’il veut traiter
dans le cadre ici explicite de la « music theory » [23].
2. Concevoir
la théorisation comme une modélisation
Second trait, dont on a pointé plus haut la logique
(néo)positiviste : Lewin thématise sa théorisation comme une
« modélisation ». Il s’agit ainsi explicitement pour lui de bâtir des
« modèles mathématico-formels » des champs musicologiques visés. Ceci
est particulièrement affirmé dans [Lewin-b] puisqu’il y déclare vouloir
construire « a formal
model for “musical perceptions” » qui va occuper toute sa Partie II : « A General Model ».
On a donc bien une connexion entre d’un côté le privilège
accordé à l’interprétation dans la théorisation et d’un autre côté la
thématisation de cette théorisation comme modélisation.
3. Concentrer
la formalisation mathématique en une formulation
Lewin présente ainsi [Lewin-a] son « modèle
formel » de perception musicale :
I propose as a provisional model for “a musical perception” this basic formula :
p = (EV, CXT, P-R-LIST, ST-LIST).
Here the musical perception p is defined as a formal list containing four arguments. The argument EV specifies a sonic event or family of events being “perceived”. The argument CXT specifies a musical context in which the perception occurs. The argument P-R-LIST is a list of pairs (pi, ri) ; each pair specifies a perception pi and a relation ri which p bears to pi. The argument ST-LIST is a list of statements s1,…, sk made in some stipulated language L. [a]
Implicitement, Lewin enchaîne trois temps :
1. un
temps préalable de formalisation où les
entités musicales d’événement sonore, de situation contextuelle, etc. sont formalisées selon l’indexation EV, CXT,
etc. ;
2. ensuite
Lewin construit dans son champ théorique la formule-clef générant p à partir de
{EV, CXT,…} ; c’est le temps de la formulation : celui qui construit la bonne formule, ajustée à son
objectif ;
3. enfin
Lewin interprète dans l’espace musical la signification de la perception ainsi
mathématiquement calculée ; c’est le temps de l’interprétation.
Soit, au total, le diagramme suivant :
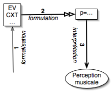
L’idée directrice est ainsi que la formulation p
= (EV, CXT, P-R-LIST, ST-LIST) peut
rendre compte de la constitution immanente d’une perception musicale comme
synthèse globale.
Une
interprétation plutôt qu’une formalisation
La schématisation du temps préalable comme formalisation
première mérite cependant d’être discutée : Lewin, pour théoriser, part
moins d’entités musicales déjà ordonnées (évènement, contexte,…)
pour les formaliser ensuite (évènement→EV, contexte→CXT,…)
qu’il ne construit sa formule selon une organisation formelle des principaux
ingrédients (EV, CXT,…) auxquels il associe une interprétation musicale (EV→évènement, CXT→contexte,…). L’exposé qu’il en fait est d’ailleurs sur ce point parfaitement explicite
(“The argument…
specifies a…”) : il expose donc une formule dont il interprète musicalement les arguments.
On doit alors détailler notre schéma en vérité de la manière
suivante : avec des flèches EV→évènements (interprétation) et non l’inverse (formalisation évènements→EV) :
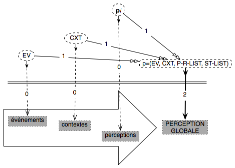
Au total, le sens caractéristique des flèches entre modèle
musical et théorie mathématique est donc celui de l’interprétation (de haut en
bas dans nos schémas) :
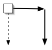
Nous résumerons alors cette manière de procéder selon le
schéma suivant où le carré initial indexe l’intervention d’une théorie
mathématique (l’algèbre des groupes chez Lewin) qui préexiste à la formulation
mathématique spécifiquement construite :
Nous désignerons cette manière de théoriser la musique avec les mathématiques comme une « application » (des mathématiques à la musique).
Figure applicative de la commutativité
Si l’on tient compte du point singulier que cette logique
d’application est le fait de musicologues, on peut pressentir que pour celui-ci
– celui-la même qui ce schème théorique -, il existe bien des déductions proprement
musicales concevables, c’est-à-dire des « d » telles que AB puisque pour le théoricien
applicatif, le modèle musical n’est pas seulement la donnée de récollection de
faits avérés sans liens entre eux, mais bien d’un champ où il lui est licite de
directement raisonner.
Autant dire que pour ce théoricien applicatif va se poser la
question singulière d’une commutativité prenant la forme suivante :
que je schématiserai
ainsi
![]()
soit : est-ce pareil d’aller de x en B en passant par y
(voie théorico-mathématique) ou par B (voie pratico-musicologique) ?
Exemple chez Carl Dahlhaus
Thomas Noll nous a récemment [24]
fourni un bon exemple d’une interrogation de ce type portée par le musicologue
Carl Dahlhaus. En effet, interrogeant la théorie de Handschin qui base le mode
sur l’échelle et l’échelle sur le cycle des quintes, ce qui conduit à mesurer
un intervalle par le nombre de quintes successives qui l’engendre (la tierce
majeure fa-la mesurerait ainsi 5 quintes fa-do-sol-ré-la), Carl Dahlhaus
objecte que la perception musicale n’opère pas ainsi - par cumulation de
quintes – mas bien plutôt par superposition de secondes majeures. Soit le
digramme suivant :
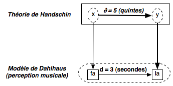
Autrement dit : non seulement la mesure
« musicale » du rapport la/fa ne s’accorde guère à la mesure
« mathématique » de Handschin, mais elle aboutit en fait à un
« la » différent car différemment perçu (dans le vocabulaire de Dahlhaus).
Donc, pour le musicologue, le diagramme ne commute pas… [25]
Subjectivité à l’œuvre
On l’aura compris : la subjectivité au principe de
cette manière de procéder conjoint deux figures.
La
figure subjective de l’ingénieur
La figure subjective de l’ingénieur est traditionnellement
celle que le positivisme, depuis Auguste Comte [26],
met en avant et c’est bien celle qu’on croise en matière de music theory (on n’y trouve guère, à proprement parler, de working
mathematician).
La
figure subjective du musicologue
Cette manière de théoriser la musique avec les mathématiques
n’a guère d’intérêt proprement mathématique. Son intérêt se concentre sur la
musique conçue comme objet de savoir, donc en une extériorité objectivante
caractéristique de la position subjective du musicologue, radicalement
différente ici d’une subjectivité de musicien (lequel se caractérise de faire la musique, de l’intérieur d’elle-même).
Philosophie spontanée
À quelles conditions philosophiques peut-on tenir tout ceci ?
Le néopositivisme du musicologue
La philosophie spontanée de cette manière de procéder [27] est clairement le néopositivisme [28], tel qu’on le trouve à l’œuvre à partir du Cercle de Vienne.
… matiné de la phénoménologie du musicien
Comme on le voit bien dans [Lewin-a], ceci n’exclut
cependant pas un recours complémentaire du musicologue théoricien à la
phénoménologie d’obédience husserlienne.
À mon sens,
ceci relève assez précisément d’une autre dimension du discours musicologique,
jusqu’ici non présentée, et qui tient cette fois au rapport de la théorie
(musicologique) qui constitue le niveau de référence pour la théorie mathématique
à la musique elle-même qu’il conviendrait alors de figurer sur notre schéma de
base par un infra-niveau 0 jusque-là implicite, en contrebas du modèle :
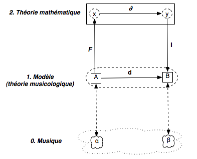
Il s’agit en effet pour le musicologue théoricien
d’interroger aussi les « valeurs de vérité » dont son modèle (sa
théorie musicologique) crédite ses entités « A », « B », …
c’est-à-dire d’évaluer musicologiquement ces valeurs de vérité en restituant
leur « signification » musicale en termes cette fois d’entités musicales
(et non plus musicologiques) « α », « β », …
Dans le cas de Lewin, cela va porter sur la signification
pratico-musicale des catégories musicologiques de « perception », de
« contexte musical », etc. C’est en ce point – celui exemplairement
du statut musical de la catégorie de perception - que le musicologue aura recours à la phénoménologie d’obédience
husserlienne en tant qu’elle constitue cette fois la philosophie spontanée du musicien.
Pour le musicien (l’homme du faire subjectivant) et non plus le musicologue (l’homme du savoir objectivé), la Phénoménologie d’obédience husserlienne [29] est la philosophie spontanée qui rend compte de son rapport à « l’objet musical », et ce de deux manières :
· en accordant une place centrale à la question du « sens » : la consistance d’un phénomène se jouerait dans son sens, dans le fait qu’il aurait ou serait un sens (ici musical) ;
· en thématisant ce sens comme constitué par une visée particulière : comme relevant essentiellement d’un « pour » quelqu’un. L’apparaître devrait être ici saisi comme apparaître « pour » un « sujet », en sorte qu’à tout apparaître, il faille supposer l’existence d’un sujet de cet apparaître.
D’où un couplage essentiel objet/sujet (où le sujet serait
constitutif du sens de l’objet) qui s’ajuste à la vision spontanée des choses
par le musicien [30].
Emblème : la music theory
L’emblème de cette manière de procéder se trouve dans la music
theory américaine, celle qui a eu Ernst
Krenek pour précurseur et Milton Babbitt pour fondateur.
II. Mathématisation (mathématicienne)
La seconde manière de théoriser la musique avec les
mathématiques – celle qu’on propose ici d’appeler « mathématisation »
— va procéder dans l’ordre inverse de la précédente : elle va privilégier
les flèches ascendantes (de bas en haut) entre modèle et théorie, la formalisation donc (en lieu et place de l’interprétation dans le cas précédent) et elle va ce faisant
orienter sa cible du côté des mathématiques et non plus du côté de la musique.
En ce sens, la subjectivité ici à l’œuvre s’avère être celle du mathématicien,
non plus du musicologue.
Exemple : Guerino Mazzola
La figure aujourd’hui la plus créatrice de cette voie se
trouve indéniablement chez le mathématicien Guerino Mazzola. Par commodité
d’exposition [31],
on se référera ici principalement à son dernier écrit : La vérité du
beau en musique (Delatour, 2007).
Rehaussons trois traits significatifs de sa manière de
théoriser la musique [32],
en bonne part symétriques de ceux relevés chez David Lewin.
1.
Privilégier la formalisation mathématique de la musique
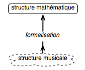
Le travail de Mazzola privilégie la flèche formalisatrice
allant de la musique vers les mathématiques. Son intérêt subjectif propre est
en effet de dégager de quelles structures mathématiques telle ou telle configuration
musicale relève. Sa subjectivité de mathématicien fait qu’il se meut à l’aise
dans la construction et la déduction mathématiques plutôt que dans la
composition et l’analyse musicales. Son mouvement de pensée vise donc à ramener
une structure musicale (qui lui est donnée) à une structure mathématique (qu’il
entreprend de caractériser) :
2.
Pour cela, partir d’une théorie musicale préexistante
Pour ce faire, Mazzola travaille non pas directement sur la
musique elle-même – sur les partitions ou les structures musicales à l’œuvre… —
mais sur une analyse existante de telle ou telle œuvre, ou sur une théorie
existante de telle ou telle dimension musicale :
·
Quand il se réfère à l’op. 106 de Beethoven, c’est
via l’analyse qu’en proposent Ratz et Uhde [b].
Quand il se réfère à Structures I.a de Boulez, c’est via l’analyse qu’en offre
Ligeti [c].
·
Quand il traite de la dimension harmonique de la
tonalité, c’est via la théorie qu’en proposent Hugo Riemann [d]
ou Schoenberg [e]. Quand il
traite de la dimension contrapuntique, c’est à travers la théorie qu’en donne
Fux [f].
Ce point est naturel pour un mathématicien qui ne saurait
fonder son propos de mathématicien sur une analyse originale et alors
nécessairement problématique du phénomène musical (comme un musicien pensif,
par contre, s’en ferait l’obligation).
3. La
cible : un développement théorique dans les mathématiques
Enfin, si l’origine de sa flèche « formalisation » est constituée par un point de vue musicologique préexistant (analyse ou théorie), sa cible mathématique va consister en un nouveau déploiement mathématique : il s’agit d’éprouver en cette affaire la capacité d’une problématique mathématique récente (ici l’informatique théorique, instruite par la théorie des topos de Grothendieck) en prenant théoriquement en charge un domaine de pensée tout à fait différent (le domaine musical) et sans rapport établi avec cette théorie mathématique. Ici la cible du travail vise à déployer ce qu’on pourrait appeler une sous-théorie mathématique d’une plus vaste théorie mathématique existante.
Le travail mathématique va donc être entièrement autre que
dans la manière précédemment examinée : non plus partir de résultats
mathématiques pour les appliquer à la musique (sans trop se soucier de leur
origine mathématique et de la manière dont leur démonstration peut rendre
compte de leur consistance propre), mais tout au contraire engager un travail
déductif et démonstratif proprement mathématique en sorte de composer une
nouvelle région de la mathématique contemporaine. C’est en ce point que le
travail de Guerino Mazzola s’affirme avec une majesté toute mathématique au fil
des 1200 pages de son The
Topos of Music [g].
Au
total…
On a donc ici le principe d’un mouvement de pensée qu’on
ramassera en un diagramme inverse de celui de l’application :
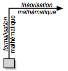
Le carré initial figure la théorie musicologique prise pour
origine.
On mesure qu’il ne s’agit pas tant, ici, de théoriser la
musique avec les mathématiques que de
théoriser mathématiquement la musique [33],
c’est-à-dire, somme toute, de mathématiser la musique. C’est à ce titre qu’on nommera cette manière de procéder
une « mathématisation ».
Remarque
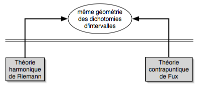
L’enjeu musicologique de cette manière de procéder ressort
clairement d’un des résultats musicalement les plus intéressants de ce
travail : Mazzola dégage comment deux théories musicales sensiblement disjointes
(l’une – celle de Fux — traite au XVIII° siècle du contrepoint, l’autre – celle
d’Hugo Riemann — au XIX° de l’harmonie) et s’ignorant l’une l’autre relèvent en
vérité d’une même géométrie des intervalles :
Le questionnement de cette manière de théoriser tend ainsi à
s’inscrire sous le schème suivant :
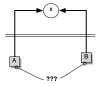
qui suscite alors la question suivante : si les entités
musicales A et B conduisent à la même structure mathématique x, qu’en est-il
alors de rapports directs, musicalement endogènes, entre A et B ?
Le désir du mathématicien va être qu’un tel rapport entre A
et B constitue ipso facto une relation musicale significative : si A et B
répondent à une même structuration mathématisante, c’est qu’il doit bien
exister une logique musicale susceptible
de les rapprocher. Soit une ligne de pensée que je formulerai ainsi [34] :
si les entités A et B sont ontologiquement apparentées, elles doivent bien l’être logiquement.
Le grand Euler, déjà, pensait ainsi puisqu’une fois sa formalisation mathématique de la suavité musicale bien établie sur la base des nombres premiers, il soutenait que les musiciens auraient à tirer parti dans l’avenir des nombres 7 et 11 sans se limiter à ceux qu’ils pratiquaient jusque-là (2, 3 et 5) - pourquoi en effet s’arrêter en si bon chemin ? Où s’insinuait déjà cette hypothèse d’une transitivité entre domaines mathématique et musical [35] via la formalisation et son interprétation…
Figure mathématisante de la commutativité
Comme le point de départ de la mathématisation est une
théorie musicologique existante, il existe à nouveau, dans cette manière de
procéder théoriquement, des morphismes à l’intérieur du modèle : ceux précisément
de la théorie musicologique prise comme point de départ.
D’où que la voie mathématisante se trouve confrontée à une
nouvelle figure de la commutativité :
![]()
que je schématiserai
ainsi
![]()
soit : est-il équivalent d’aller de A en y en passant
par x (voie mathématique) ou par B (voie musicologique) ?
Exemple chez Mazzola
Mazzola nous fournit un bon exemple de cette question quand
il formalise l’opus 106 de Beethoven en α, en déduit mathématiquement α’
et élabore un morceau de musique (son opus 3) tel qu’il soit lui-même formalisable
en α’. La question – implicite chez Mazzola mais amplement suggérée [36]
- est alors : existe-t- il une variation musicale « var » αα’ [α’=var(α)] telle que le
diagramme ci-joint commute ?
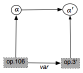
On verra en annexe 1 comment Mazzola en ce point répond en
tentant de ressuciter le mythe pythagoricien d’une mathémusique…
Subjectivité à l’œuvre
La subjectivité à l’œuvre dans cette mathématisation de la
musique est clairement mathématicienne : c’est d’ailleurs elle qui ouvre
puis conclut le dernier livre de Mazzola, dans une tonalité subjective joyeusement
exaltée [37]…
C’est la même subjectivité mathématicienne que celle d’Euler
travaillant à théoriser mathématiquement la musique au XVIII° — on sait que son
intérêt subjectif était alors d’éprouver l’unité des mathématiques, alors en
plein foisonnement disciplinaire (naissance de l’analyse in situ, de la théorie des graphes, explosion de la combinatoire…),
en les mettant à l’épreuve d’avoir à rendre compte des différentes dimensions
du phénomène musical - [38].
Philosophie spontanée ?
Mon hypothèse (provisoire ?) est qu’il n’y a pas de
philosophie spontanée caractéristique de cette manière mathématicienne de
théoriser la musique [39].
En un certain sens, les mathématiciens ici à l’œuvre n’ont guère besoin d’une
philosophie particulière pour légitimer leur entreprise de mathématisation,
laquelle constitue, en un certain sens, leur tâche quotidienne. [40]
Deux manières symlétriques de théoriser
On a jusqu’ici dégagé deux manières de théoriser la musique
avec les mathématiques, sensiblement symétriques :
|
|
application
|
mathématisation
|
|
|
La théorisation circule |
de la mathématique vers la musique |
de la musique vers la mathématique |
|
|
La théorisation est le fait |
d’un ingénieur pour un musicologue |
d’un mathématicien prenant appui sur le travail d’un musicologue |
|
|
|
La formalisation est |
secondaire |
capitale |
|
La déduction est |
une formulation |
l’enjeu |
|
|
L’interprétation est |
l’enjeu |
une retombée justificatrice |
|
|
La question d’une commutativité prend ici la forme |
|
|
|
Mais cette dualité n’épuise pas les possibles en matière de théorisation de la musique avec les mathématiques.
III. Expérimentation (musicienne)
Une troisième manière de procéder s’est affirmée au sein de mamuphi, manière de part en part musicienne (ni musicologique,
ni mathématicienne) qui traite tout autrement de la polarité
musique/mathématiques.
L’idée générale est la suivante : il ne s’agit plus de
constituer un rapport par rapprochement de domaines préexistants (dans l’application, on rapproche une théorie mathématique existante d’un domaine musicologique donné, et dans la mathématisation on rapproche une théorie musicologique existante d’un domaine mathématique donné) mais de constituer d’un même geste les deux pôles
d’un nouveau rapport selon le schème suivant :
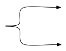
Rapport constituant plutôt que constitué
Le rapport modèle/théorie n’est plus ici constitué (par rapprochement, par mise en rapport de réalités
préexistantes) mais constituant
des deux termes qu’il va relier.
Conformément à la tradition bachelardienne, on appellera ce schéma « expérimentation » car il s’y agit de constituer un espace de pensée où expérimenter les rapports entre la matérialité d’une expérience et sa formalisation théorique.
Espacement plutôt que rapprochement
Le geste constitutif de cette manière de procéder n’est donc
plus un rapprochement entre domaines séparés
mais un espacement instituant
deux pôles en interaction, deux manières de « dire la
musique » : l’une selon la langue ordinaire (dans le modèle), l’autre
selon le mathème (dans la théorie) :
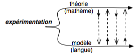
Musicien plutôt que musicologue
Cette expérimentation sera dite musicienne car elle est le propre d’une pensée se déployant en
intériorité à la pratique musicale, au « faire (de) la musique ».
Elle ne traite pas la musique comme objet extérieur faisant face à un
observateur mais comme projet auquel le musicien expérimentateur participe. Et
c’est bien au titre de cette participation, et dans une visée réflexive ou
pensive, que le musicien entreprend de théoriser tel ou tel aspect de ce
« faire (de) la musique ».
Un nouveau sens de ce que « théoriser » veut musicalement dire
Il va de soi qu’ici « théorie » aura donc un sens
légèrement différent de celui qu’il avait dans les deux autres manières, de
même d’ailleurs que les mots « musique » et
« mathématique » : cette « théorie » ne se qualifie
plus par son supposé « objet » mais par ses enjeux subjectifs ; on part ici clairement d’un problème
et, pour le travailler, on monte un dispositif expérimental singulier à deux
pôles (théorie/modèle) apte à constituer un espace de pensée adéquat.
Une telle théorie musicienne de la musique n’a pas d’idéal de scientificité (la théorie n’est plus ni véritable science — comme la mathématique dans l’orientation mathématisante -, ni pseudo-science humaine — comme dans l’application musicologique -), et ce même si cette théorie, convoquant la mathématique, se fait bien avec l’appui de la mathématique, appui dont la trace formelle dans la théorie musicienne va prendre la forme singulière du mathème…
Des « faits » constitués plutôt que constituants
La théorie ici en jeu n’a plus de « faits » constituants, comme elle pouvait avoir la formule ou l’équation mathématiques dans l’application musicologique, les résultats des théories musicologiques convoquées dans la mathématisation mathématicienne, mais ses « faits » seront constitués par elles : ils seront des résultats de la dialectique d’espacement et d’expérimentation entre expérience et formalisation.
Voyons comment.
*
Je convoquerai ici comme exemple mes propres travaux
théoriques.
Trois exemples
Dans chacun des trois exemples qui vont suivre, le point de
départ sera un problème qu’il s’agit d’arriver à penser quand bien même aucun
outil théorique répertorié n’existe pour ce faire. Il s’agira donc chaque fois
d’inventer un cadre de travail ajusté au problème singulier qui initie la
recherche.
1. Théorie
de l’audition musicale
Le problème de départ était ici d’arriver à différencier
musicalement l’audition, d’un côté de la perception, et d’un autre côté de
l’écoute [41].
L’idée de départ pour traiter ce problème était la
suivante : et si l’audition, conçue comme une perception totalisante,
opérait (en un sens à préciser) comme opère une intégration mathématique ?
À quelles conditions serait-il ainsi possible de penser plus avant l’audition
musicale sous l’hypothèse d’une mise en parallèle
?
Il s’agissait, à partir de là, de monter un dispositif
expérimental qui permette de tester la validité de cette hypothèse de travail.
D’où l’examen simultané des différents types d’audition musicale communément
pratiqués et des différents types d’intégrale inventés par les mathématiciens à
partir de Riemann [42].
L’expérimentation tenait alors à la capacité de mettre en rapport de
formalisation/interprétation les différentes auditions et les différentes
intégrales :
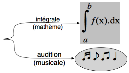
Le résultat a été la mise en rapport détaillé d’un côté de
trois types d’intégrale (chronologiquement ordonnés par l’histoire
mathématique : Riemann, Lebesgue, Kurzweil-Henstock), de l’autre de trois
types d’audition (spontanée, perceptive, réflexive), chronologiquement ordonnés dans l’appréhension musicienne d’une même
pièce :
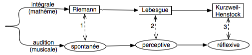
On trouvera le détail du compte rendu et des résultats de
cette expérimentation dans mon article « La troisième audition est la
bonne (De l’audition musicale conçue comme une intégration) » [h].
2. Théorie
de l’écoute musicale
Le problème de départ était cette fois le suivant :
comment rendre compte du travail musical de l’écoute, de l’écoute musicale
comme activité immanente à l’œuvre ?
Ce problème s’inscrivait dans le champ plus général d’une
théorie musicale de l’écoute dont les catégories essentielles sont : moment-faveur, préécoute, fil d’écoute, intension et inspect [43]. Dans ce
cadre, se posait en particulier la question précise suivante : comment,
après le moment-faveur, l’écoute musicale trace-t-elle un fil qui traverse
l’œuvre de part en part, un fil d’écoute constituant le fil rouge (ou fil
conducteur, ou filigrane) de son opération globale propre ?
L’idée de départ m’a été inspirée par l’extraordinaire
article Le problème du temps d’Albert
Lautman [44] où celui-ci
montre comment les mathématiques reconstituent la structure dissymétrique du
temps dans les opérations d’intégration d’une équation différentielle [45] :
ne pourrait-on alors comprendre le travail de l’écoute musicale à partir d’un
certain moment (à partir très précisément du moment-faveur) comme tricotant un
temps spécifiquement musical au fil de la chronologie de l’œuvre selon des
opérations équivalentes à celles des mathématiques ?
À partir de là, il s’agissait de monter un dispositif
expérimental qui dualise d’une part les opérations musicales de l’écoute et
d’autre part les opérations d’intégration différentielle telle que Lautman les
avait exhaussées :

Le Leitfaden
est le suivant : le moment-faveur fait émerger une dimension musicale
privilégiée (au sein du discours musical à l’œuvre). À partir de là, l’écoute
s’attache à cette dimension particulière pour paramétrer et intégrer l’intension musicale globale, tricotant progressivement une
synthèse rythmique où cette dimension privilégiée joue un rôle dissymétrique,
donnant ainsi à cette synthèse la forme synthétique d’un « temps
musical ».
Le champ expérimental ainsi déployé peut être diagrammatisé
de la manière suivante :
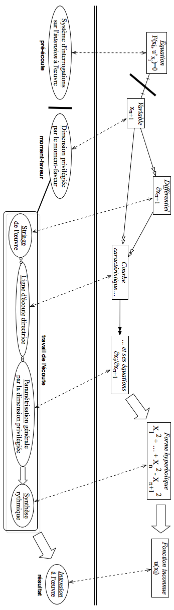
3. Formalisation
des rapports cinématographiques musique-paroles-images dans Muriel
Prenons un dernier exemple, attaché cette fois à un autre
art (l’art du cinéma), pour indiquer la généralité de la manière expérimentale
ici avancée.
Le problème de départ était cette fois de rendre compte d’un
effet sensible éprouvé lors de la vision, il y a bien longtemps, du film Muriel de Resnais et tenant en particulier au jeu très
prégnant, dès le générique, de la musique « sérielle » d’Henze. Cette
musique, nullement illustrative, ne cessait au cours du film d’apparaître et de
disparaître, sans principe identifiable, laissant son empreinte sur la vision
du film sans que j’arrive à comprendre comment cela était cinématographiquement
composé.
L’idée de départ était la suivante : ne pourrait-on
comprendre le jeu de nouage et de chassé-croisé entre les trois composantes de
ce film (les images de Resnais, les paroles de Cayrol, la musique d’Henze)
comme relevant d’une structure borroméenne ?
D’où l’idée de monter un dispositif expérimental permettant
de mettre systématiquement en rapport les relevés minutieux des trois
composantes images/mots/musique (présence/absence, en compagnie ou non de telle
composante) et une formalisation algébrique du nouage borroméen [46] :

Cette manière de procéder a permis de mettre en relief la
manière cinématographique dont les trois composantes du film se rapportent à
tour de rôle deux à deux, selon une logique à chaque fois infléchie par la
troisième composante provisoirement absente. [47]
Traits caractéristiques
Dessinons, à partir de là, les principaux traits
caractérisant cette troisième manière de théoriser la musique avec les mathématiques.
Fiction
La théorisation peut ici mobiliser ce qu’on appellera une
fiction de modèle (ou modèle fictif) puisqu’il s’agit dans notre premier
exemple d’expérimenter l’hypothèse suivante : faisons comme si l’audition
musicale constituait un modèle pertinent de la théorie mathématique de
l’intégration (qui, bien sûr, a été conçue à de tout autres fins). Si l’on
associe la logique du « comme si » à la fiction, réservant celle du
« comme » à la métaphore (rapprochement de deux termes) ou à
l’analogie (rapprochement de deux rapports), alors on admettra, conformément au
propos de Lacan (« la vérité a une structure de fiction »), qu’une
vérité puisse procéder d’une telle dynamique fictionnelle [48].
Mathèmes
Plus largement, le
recours aux mathématiques dans cette logique d’expérimentation s’avère très
particulier : il s’agit en vérité de mobiliser des mathèmes, composés ad
hoc, et nullement des formules ou équations à appliquer. Le mathème met en
forme littérale une concrétion de pensée, se tenant à égale distance de la
logique démonstrative et de la logique calculatoire.
La forme-mathème est ajustée à la saisie du contenu de pensée proprement ontologique des mathématiques : il lui donne la frappe d’une formule littérale qui se dispose à l’intersection de multiples domaines.
Cette modalité spécifique est adaptée au fait qu’il s’agit ici moins de théoriser des structures musicales (dimension ontologique) ou de formaliser mathématiquement la consistance propre du discours musical (dimension logique) que de caractériser ce qu’il en est spécifiquement des œuvres musicales par différence d’avec de simples pièces ou morceaux de musique [49]. C’est ici le mathème qui constitue la forme littérale adéquate s’il est vrai que les mathématiques proprement dites, science de l’être en tant qu’être (ontologie), ignorent le sujet comme tel…
« Théoriser », en un autre sens du terme…
« Théoriser »
désigne ici des pratiques singulières, non épongeables dans les schèmes
positivistes de la « scientificité ».
Théoriser veut bien
dire, ici comme ailleurs, formaliser et généraliser, mais formalisation et
généralisation prennent ici des formes singulières, non ordonnées au régime
mathématique de consistance. En particulier les énoncés théoriques ainsi
produits par l’expérimentation musicienne ne seront pas à proprement parler ni
démontrés, ni réfutables, ni falsifiables quoiqu’ils soient fortement
argumentés et rationnellement soutenus (un peu comme le discours que je suis
ici en train de soutenir).
En vérité, les énoncés
théoriques dont il est question dans une théorie proprement musicienne (et non
pas musicologique) sont de nature prescriptive et non pas descriptive. Ils
procèdent d’une rationalité qui s’attache à convaincre, à argumenter, à
clarifier et distinguer, qui se soumet à une discipline rigoureuse des conséquences
des énoncés avancés, mais si tout ceci prend bien modèle sur le discours
mathématique (d’où le « mathème »), il ne s’agit cependant nullement
de faire ici des mathématiques.
Prenons ainsi les
trois énoncés théoriques auxquels les trois expérimentations données précédemment
en exemple aboutissent :
·
« La troisième audition est la bonne. »
·
« Toute écoute procède d’un moment-faveur. »
·
« Muriel est le nouage borroméen des
images de Resnais, des paroles de Cayrol et de la musique de Henze. »
On soutiendra qu’il
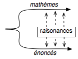
s’agit bien d’énoncés théoriques car ils formalisent et généralisent [50] en sorte de constituer des espaces
d’investigation et d’intelligence musicienne.
Théoriser consiste donc ici à passer d’hypothèses subjectivement [51] assumées par le musicien – énoncés de départ, au principe de l’interrogation et donc de l’expérimentation – à des thèses formalisées et généralisées (énoncés qui conservent bien sûr le même statut subjectif).
Philosophie
C’est aussi à tous ces titres que cette manière de procéder
convoque assez directement la philosophie (celle de Lautman par exemple) car
celle-ci tend à dégager le contenu ontologique de la mathématique en le
reformulant dans la langue commune, autorisant ainsi le musicien à transposer
les catégories mathématiques en notions communes via les concepts
philosophiques [52].
Raisonances
À ce titre, les rapports verticaux entre théorie et modèle
(les formalisations et interprétations) s’avèrent des raisonances.
Au
total…
On a donc ici le schéma suivant, où l’expérimentation
s’avère rapport constituant des raisonances entre mathèmes et énoncés :
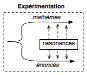
Philosophie spontanée
On l’aura compris : la philosophie susceptible
d’accompagner en pensée cette manière de faire est celle qui donne droit :
·
d’une part à la science comme pensée, et non comme jeu
de langage, bien-dire, ou technique de manipulation des étants ;
·
d’autre part à l’art également comme pensée, pensée
autonome, donc non normée par la science [53] ;
·
ensuite à la philosophie comme réfléchissant, pour son
compte propre [54],
les contemporanéités éventuelles entre pensées essentiellement
hétérogènes ;
·
enfin à la pensée comme travail visant à faire émerger
telle ou telle figure de vérité accompagnée des indispensables nouveaux énoncés
que cette procédure suscite.
Un petit bouquet de citations pour indiquer où trouver de
telles philosophies.
Gaston
Bachelard [55]
·
« On ne peut parler les mathématiques sans les
comprendre mathématiquement. » [56]
·
« Il faut rompre avec ce poncif cher aux
philosophes sceptiques qui ne veulent voir dans les mathématiques qu’un
langage. Au contraire la mathématique est une pensée. » [57]
·
« Avant tout, il faut savoir poser des problèmes.
Et quoi qu’on en dise, dans la vie scientifique, les problèmes ne se posent pas
d’eux-mêmes. C’est précisément ce sens du problème qui donne la marque du véritable esprit scientifique.
Pour un esprit scientifique, toute connaissance est une réponse à une question.
S’il n’y a pas eu de question, il ne peut y avoir connaissance
scientifique. » [i]
·
« L’esprit peut changer de métaphysique ; il
ne peut se passer de métaphysique. » [58]
·
« Toute expérience sur la réalité déjà informée
par la science est en même temps une expérience sur la pensée scientifique. »
[59]
Albert
Lautman
·
« Il ne suffit pas de poser la dualité du sensible
et de l’intelligible ; il faut encore expliquer […] la genèse du sensible
à partir de l’intelligible. Or les mathématiques fournissent justement, dans
certains cas, des exemples remarquables de détermination de la matière à partir
de la forme ». [j]
· « Que
l’expérience mathématique soit la condition sine qua non de la pensée mathématique, cela est certain. » [k]
· « Les
mathématiques appartiennent bien au domaine de l’action. » [l]
· « La
raison des rapports de la dialectique et des mathématiques réside dans le fait
que les problèmes de la dialectique sont concevables et formulables
indépendamment des mathématiques, mais que toute ébauche de solution apportée à
ces problèmes s’appuie nécessairement sur quelque exemple mathématique destiné
à supporter de façon concrète la liaison dialectique étudiée. » [m]
·
« La véritable logique n’est pas a priori par rapport aux mathématiques mais il faut à la
logique une mathématique pour exister. » [n]
Jean
Cavaillès
·
« L’activité des mathématiciens est une activité
expérimentale. » [o]
·
« C’est d’une épistémologie naïve que faire naître
les objets mathématiques par abstraction à partir du réel. En fait, il y a
développement autonome d’opérations qui, dès l’origine, sont
mathématiques. » [p]
·
« L’activité des mathématiciens est une activité
expérimentale. Par expérience, j’entends un système de gestes, régi par une
règle et soumis à des conditions indépendantes de ces gestes. » [q]
·
« La résolution d’un problème possède tous les
caractères d’une expérience :
construction soumise à la sanction d’un échec possible, mais accomplie
conformément à une règle. » [r]
Alain
Badiou [60]
·
« Loin d’indiquer un dehors de la pensée formelle,
la théorie des modèles règle une dimension de l’immanence pratique des
sciences, de reproduction des conditions de production. » [s]
·
« Le concept de modèle ne désigne pas un dehors à
formaliser mais un matériau mathématique à éprouver. » [t]
·
« Les systèmes formels sont le temps expérimental,
l’enchaînement matériel de la preuve, après celui, conceptuel, des démonstrations. »
[u]
·
« Toutes les sciences sont expérimentales. » [v]
·
« Modèle
désigne l’articulation conceptuelle, pour autant qu’on la rapporte à un
dispositif expérimental particulier : un système formel. » [w]
Postlude
Récapitulation
Récapitulons les traits distinctifs de nos trois manières mamuphi de théoriser la musique avec les mathématiques.
|
|
I. Application |
II.
Mathématisation |
III.
Expérimentation |
|
|
|
|
|
|
Acteur subjectif : |
le musicologue |
le mathématicien |
le musicien pensif |
|
La question de la commutativité mathématiques/musique prend la forme suivante : |
|
|
ne s’y pose plus ! |
|
Rapport subjectif aux mathématiques du type : |
ingénieur |
mathématicien |
philosophique |
|
Théoriser, c’est |
construire une formule (ou une équation) |
mathématiser |
formaliser la logique proprement musicale du monde-Musique |
|
Enjeux de cette théorisation : |
produire, en extériorité objectivante, de nouveaux savoirs sur la musique |
élargir la puissance ontologique des mathématiques |
approfondir la connaissance musicale |
|
La musique concernée, c’est |
les systèmes musicaux |
une théorie musicologique préexistante |
des énoncés musiciens sur les œuvres musicales |
|
La musique est |
une cible |
une origine |
un espace de pensée |
|
La mathématique est |
une origine |
une cible |
l’ontologie |
|
Les mathématiques impliquées prennent la forme de |
formules &
équations |
théories (en développement) |
mathèmes |
|
Les rapports musique-mathématiques privilégient |
les interprétations |
les formalisations |
les raisonances |
|
La mathématique touche de préférence |
au discours musical |
aux structures musicales |
aux œuvres musicales |
|
Philosophie spontanée : |
le positivisme logique |
|
de Bachelard à Badiou |
3=2+1 !
Notre 3 s’avère
ainsi relever d’un 2+1 puisqu’il y a bien d’un côté une symétrie application|mathématisation,
et de l’autre une position excédentaire qui se s’exempte de la dualité
précédente.
Si l’on récapitule
les traits distinctifs qui partagent ce 3 en un 2|1, on a ceci :
·
Rapprochement constitué / espacement constituant
·
Mathématiques strictes / mathèmes
·
Pièces de musique / œuvres musicales
·
Théorie musicalement descriptive / prescriptive
·
…
Intersubjectivités ?
On a mis ici l’accent sur la dimension subjective du travail
de théorisation. C’est elle qui a présidé à la différenciation des trois
manières. C’est elle qui légitime l’examen symptomal et non pas systématique
des trois théories particulières convoquées comme exemples.
On pourrait alors accentuer ce trait de la manière
suivante : une théorie mathématique peut être conçue comme ce qui tient
lieu de sujet mathématique, de même qu’une œuvre musicale peut être conçue
comme ce qui tient lieu de sujet musical. C’est là très exactement la thèse
philosophique d’Alain Badiou à laquelle je me rallie : le véritable sujet
en mathématique n’est pas plus le mathématicien qu’il n’est en musique le
musicien [61]. Le mathématicien,
comme le musicien, n’est qu’un individu venant prêter un temps – le temps où il
travaille – son corps physiologique au corps subjectivé de la théorie ou de
l’œuvre [62].
Si donc « théorie » désigne le sujet mathématique,
et « œuvre » le sujet musical, on voit que le projet de théoriser mathématiquement l’œuvre musicale reviendrait à créer l’espace
original d’une véritable intersubjectivité :
≡
Comme indiqué au début de ce texte, le programme mamuphi n’est pas exactement celui-là : il ne s’y agit
pas de « théoriser mathématiquement l’œuvre musicale » mais de
« théoriser la musique avec les mathématiques ». L’écart est notable.
Il l’est cependant moins dans la seconde manière ici
intitulée « mathématisation », et plus encore, comme on pourra le
voir en annexe, dans sa modalité mazzolienne : c’est en effet très
exactement au point d’une intersubjectivité impensée que Mazzola convoque le
mythe d’une « adjonction » réduisant la fracture entre deux
discursivités hétéronomes (mathématique et musical) et pointant vers un
méta-monde réconcilié…
Y aurait-il alors moyen de penser – non
mythologiquement - une véritable intersubjectivité entre mathématiques et
musique ?
À bien y regarder, ce point est débattu depuis le début de mamuphi, en particulier sous la forme de cette
interrogation : que vient faire la philosophie en cette affaire ? [63]
Peut-on relier directement mathématiques et musique ou faut-il nécessairement
en passer par la philosophie ?
Les manières « application » et
« mathématisation » soutiennent une telle possibilité directe. La
manière « expérimentation » est déjà plus réservée. Mais comme on l’a
vu, dans aucun de ces trois cas il ne s’agit à proprement parler de relier
directement une théorie mathématique et
une œuvre musicale :
·
dans l’application, la théorie mathématique n’est pas traitée comme telle mais
seulement comme dispensatrice de résultats, c’est-à-dire de savoirs
objectivés ;
·
dans la mathématisation, c’est l’œuvre musicale qui n’est plus traitée comme telle ;
la musique n’est pas saisie comme projet subjectif à l’œuvre mais comme réseau
structurel de notions dégagées par la musicologie ;
·
enfin dans l’expérimentation, il s’agit, on l’a vu, de
mathèmes plus que de théories
mathématiques proprement dites, et d’énoncés sur les œuvres plutôt que
directement de ces œuvres.
Bref, l’espace de travail mamuphi, s’il touche bien aux rapports intersubjectifs [64]
entre mathématiciens, musiciens et musicologues n’est pas pour autant
l’exploration d’une intersubjectivité véritable entre sujet mathématique
(théorie) et sujet musical (œuvre).
*
Je terminerai en ce point ce petit bilan mamuphi sur une thèse : de tels rapports directs ne
sauraient à mon sens exister car il n’y a rigoureusement aucune possibilité
qu’une théorie mathématique rencontre une œuvre musicale (ou même s’y frotte),
et bien sûr vice versa. Seule la philosophie peut tenter d’examiner leur
contemporanéité éventuelle [65]. Seule une prise en compte de la philosophie
pour elle-même dans le cadre général d’un nouage mamuphi permettrait d’éclairer autrement le projet de
théoriser la musique avec les mathématiques et, sans doute, de compléter la
typologie ici esquissée [66].
On comprendra que cette conclusion vaut appel à contribution
des philosophes, pour la suite d’un working
mamuphi…
————————
Annexes
Annexe 1 : Le mythe pythagoricien d’une « mathémusique »
Si, comme on l’a vu,
le travail de Guerino Mazzola est exemplaire de cette mathématisation contemporaine
de la musique qui reprend, dans un tout autre contexte mathématique, le
flambeau d’Euler, d’un autre côté ce travail assortit cette mathématisation de
tout autres considérations qui tendent cette fois à constituer ce que
j’appellerai le mythe pythagoricien d’une « mathémusique ».
On peut en effet
relever dans le travail de Mazzola quatre particularités qui supplémentent la
mathématisation précédemment examinée :
1)
d’abord Mazzola complète sa mathématisation avec
différentes applications ; ce geste, nouant nos deux
premières manières de théoriser la musique (mathématisation ⊗ application),
ne pose pas en soi de problème particulier ;
2)
une orientation particulière se dessine cependant quand
Mazzola minore le basculement des subjectivités (mathématicienne/musicologique)
à l’œuvre dans ces deux manières de théoriser la musique pour promouvoir une continuité du geste
global ainsi généré (ce qui va prendre la forme technique d’une thèse implicite
qu’on dira celle des voisinages induits) ;
3)
Mazzola surdétermine ensuite cette continuité supposée
du geste mathématisation⊗application en
convoquant une complémentarité supposée des pensées
mathématique et musicale (cela prendra la forme technique d’une thèse
explicite d’adjonction) ;
4)
Mazzola soutient enfin que cette complémentarité est
constitutive d’une sorte de méta-monde, d’un « univers » réunifiant
les divers mondes de la mathématique et de la musique, Cosmos réconcilié qu’on
propose ici, à la suite de Moreno Andreatta, de nommer mathémusique [67].
Soit le processus
suivant, dont on va voir qu’il relève proprement d’une mythologie
contemporaine, plus exactement de la réactivation/résurrection moderniste d’un
mythe pythagoricien :
nœud mathématisation ⊗ application
⇒
continuité du geste Å complémentarité d’une
adjonction
⇒
réconciliation des mondes dans un Cosmos
mathémusical
1. Nœud mathématisation⊗application
Mazzola complète
d’abord sa mathématisation par des applications spécifiques, dont la méthode
est conforme aux orientations présentées dans notre première partie. [68]
C’est par exemple le
cas
· pour
sa théorie de l’interprétation [x],
· pour
sa théorie de la gestuelle de la main du pianiste [y]…
Le nouage d’une
mathématisation et d’une application génère alors le diagramme suivant :
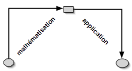
Le point singulier,
subjectivement significatif, est que Mazzola s’autorise de ce nouage pour
progressivement interpréter ce diagramme selon le schème implicite
suivant :
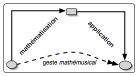
Voyons comment.
2. Continuité d’un geste (ou thèse des
voisinages induits)
Mazzola plaide
d’abord que la mathématisation ainsi complétée d’applications ad hoc devrait
intéresser le musicologue (et pas seulement le mathématicien) puisqu’elle est
ainsi rendue susceptible d’élargir les savoirs sur la musique.
Pour valider ce
point de vue, Mazzola va argumenter que le passage par la théorie mathématique
permet de composer de véritables voisinages musicaux (d’ajouter, par exemple, à
la Hammerklavier, op. 106, de Beethoven une œuvre qui lui serait
apparentée : L’essence du Bleu, op. 3 de Mazzola [69]).
Voici en effet son
schéma [z], suivi de sa redisposition conforme à notre
manière de diagrammatiser :
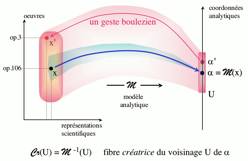 soit
soit
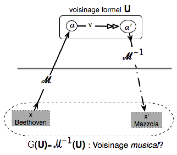
La dynamique est la
suivante :
1.
formaliser l’œuvre musicale x en une formulation
mathématique α=ℳ(x) ;
2.
varier mathématiquement α : α’=v(α)∈U
(voisinage mathématico-formel produit par la variation mathématico-formelle v) ;
3.
interpréter α’ en une nouvelle entité musicale x’=ℳ-1(α’)
avec x’∈ℳ-1(U)=G (U).
La thèse - qu’on
nommera « thèse des voisinages induits » - consiste
à poser que le « voisinage » de x (ici nommé « fibre
créatrice » et figuré par un ovoïde vertical de même forme et de même
couleur que U) auquel x’ appartient (au simple titre du fait que α’ est
mathématiquement voisin de α) pourrait être considéré comme un voisinage
proprement musical ; autrement dit, x’ pourrait être considéré comme une
variation musicale de x puisque α’ est une variation mathématique de α. Ce qui
s’inscrit ainsi :
ℳ-1°v°ℳ(x)
= Voisinage musical de x
Selon cette thèse –
restant implicite chez Mazzola - une variation mathématique v
génératrice d’un voisinage mathématique U induirait
une variation musicale x→x’ interne à un voisinage musical ℳ-1(U) [70].
Remarque
En vérité, cette
thèse pourrait prendre plus naturellement la forme d’une commutativité si l’on
remarque que la flèche ℳ-1 ne saurait avoir, dans cet
exemple, un statut de fonction inverse : ℳ-1 est
multiforme au sens où de nombreuses pièces musicales xn
sont susceptibles de répondre à la même formalisation α’. En vérité x’=ℳ-1(α’)
veut simplement dire α’=ℳ(x’), et l’on a donc en vérité le
diagramme suivant :
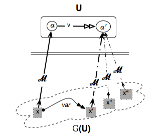
D’où la
question : existe-t-il une transformation musicale « var » telle
que
1) x’=var(x)
[s’entend : x’ varie musicalement x] ;
2) le diagramme
suivant commute : ℳ°var=v°ℳ ?
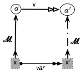
Notons que Mazzola
ne pose pas la question du voisinage induit sous cette forme d’une
commutativité des variations mathématique (v) et musicale (var), mais sous
celle d’une fibre créatrice G(U) dans laquelle le lien entre x et x’ n’est pas
précisé.
Le point reste
cependant de savoir si le G(U) ainsi construit constitue ou non un voisinage
musical de x (ce que le graphisme suggère), si la topologie induite sur
l’espace des opus par ce geste ℳ-1°v°ℳ
correspond donc bien à la topologie proprement musicale des opus, bref si x’ (L’Essence
du Bleu, op. 3 de Mazzola) est musicalement voisin de x
(la Hammerklavier, op. 106 de Beethoven).
Or il est manifeste,
pour un musicien, que L’Essence du Bleu ne saurait être comprise comme
une variation musicale pertinente de la Hammerklavier. Qu’il
suffise, pour en attester, de rapprocher dans ces deux « sonates » le
même enchaînement : entre la fin de l’exposition et le début du
développement.
|
Beethoven Hammerklavier (op. 106) |
Mazzola L’essence du bleu (op. 3) |
|
|
|
Au total, Mazzola
suggère qu’il y aurait une forme de transitivité entre mathématiques et
musique, une transitivité des voisinages, donc des topologies, transitivité qui
n’est qu’une étape dans la constitution d’un horizon mathémusical [71].
3. Complémentarité mathématiques-musique (ou
thèse de l’adjonction)
Ce geste constitutif
d’une transitivité n’a pas un statut purement local dans la théorie de Mazzola.
Outre le fait qu’il occupe un chapitre entier [aa] de son dernier livre, outre le fait qu’il le
réitère ensuite sur Structures Ia de Boulez, ce geste tend à
consolider une thèse que l’on trouve cette fois explicitement sous la plume de
Mazzola [72], thèse d’une pure et simple adjonction entre
musique et mathématiques. Je le cite :
·
« Tandis que l’activité du mathématicien crée
la mise en formule de gestes, celle du musicien crée la mise en gestes de
formules. Ces compétences sont parfaitement complémentaires, ce que nous représentons
par un diagramme montrant l’association des processus.
![]()
Mathématiquement
parlant on a ici la situation d’une adjonction de foncteurs. » [bb]
· « Nous
avons donné [de la tension profonde entre l’action du faire et la pensée du
fait] une très courte description au cours du chapitre introductif, par un
diagramme “d’adjonction” de processus. Ces deux partenaires adjoints ne sont
pas, dans les modèles présents, unifiés, mais définissent les limites d’un
dynamisme musico-mathématique de nature “ping-pong”, un système commutatif
riche, bien sûr, mais pas encore une cohabitation de deux aspects partiels d’un
univers complet et cohérent. » [cc]
Cet « univers
complet et cohérent » [73], Mazzola l’appelle bien sûr de ses vœux,
moyennant « l’abolition de l’amour-haine entre la science et
l’art » [dd], et la promotion d’« un esprit
singulier de communication mathémusicienne » [ee].
Remarque
On remarquera que
Mazzola conçoit ici « musique » et « mathématiques » comme
foncteurs et non plus comme catégories ou topos… Il y aurait alors lieu
d’interroger la manière dont les agrégats fortement hétérogènes de formules à
la fois mathématiques et musicales d’un côté, de gestes à la fois mathématiques
et musicaux de l’autre, sont susceptibles de constituer des catégories en sorte
que les deux foncteurs ici désignés « musique » et
« mathématiques » puissent être adjoints.
En vérité, ces
énoncés suggérant l’adjonction participent déjà du mythe que Mazzola entreprend
d’édifier en sorte de réduire un abyme qu’il juge problématique entre
mathématiques et musique.
4. La réduction mythologique de la séparation
mathématiques|musique
Il me semble en
effet requis d’interpréter l’ensemble de cette « cause » mazzolienne
comme une véritable cause mythologique, au sens très précis que Claude
Lévi-Strauss nous a appris à entendre dans le mythologique (ou logique des mythes),
soit l’idée suivante : la logique mythique consiste, face à une opposition
radicale, d’entreprendre de la réduire (comme on réduit chirurgicalement une
fracture) par construction de deux nouveaux termes plus rapprochés que les
termes initialement opposés.
Claude Lévi-Strauss
nous fournit le mathème de cette réduction mythologique dans sa « formule
canonique du mythe » [74] :
|
X(a) |
↪ |
X(b) |
|
Y(b) |
A-1(y) |
Soit l’idée
suivante : face à l’opposition entre le terme a portant la
valeur X et le terme b portant la
valeur Y, le mythe va lui substituer l’opposition réduite du terme b assumant
désormais la valeur X et d’un nouvel acteur y (substantivant
l’ancienne valeur Y) portant une nouvelle valeur A-1
(dérivée de l’acteur a inversé).
Le mythe que Mazzola
nous instruit tout au long de son dernier La vérité du beau en musique, en complément
de sa mathématisation par ailleurs incomparable, est ainsi formalisable selon
le mathème suivant :
|
Vérité (de la mathématique) |
↪ |
Vérité (de la musique) |
|
Beauté (de la musique) |
Informatisation (du beau) |
Ce qui se dira
ainsi : la contradiction que Mazzola ressent comme insupportable entre la
musique porteuse de « beauté » et la mathématique porteuse de
« vérité » sera mythologiquement réduite en lui substituant le
nouveau couple, plus apaisé, formé d’un côté par une musique désormais capable
de vérité (« la vérité du beau en musique ») et d’un autre côté par
un beau susceptible désormais d’informatisation (entendue comme calcul déposé
par une pensée mathématique évaporée) : voir dans ce livre le cortège des
logiciels - Presto, Rubato, etc. - calculant la beauté des
interprétations musicales… [75]
*
Que la production
mythologique d’un tel méta-monde mathémusical puisse se
nourrir ainsi de la pratique mathématique la plus précise et la plus
actuelle [76] ne doit pas nous étonner : elle est ici
clairement au principe de la réduction d’une fracture subjective chez son
auteur, entre la figure du mathématicien nourri d’informatique théorique et celle
du musicien improvisateur nourri de Cecil Taylor [77].
Annexe 2 : Mamuphi
Petite chronologie mamuphi
·
Décembre 1999 : Forum Diderot « Mathématique et musique » de la SME [ff]
·
2000-2001 : Première année du séminaire mamuphi (à l’Ircam) [gg]
·
À partir de l’automne 2001 : Séminaire MaMuX (à l’Ircam) [dir. C. Agon, M. Andreatta]
·
À partir de l’automne 2004 : Reprise du séminaire mamuphi, à l’Ens [dir. C. Alunni, M. Andreatta, F. Nicolas]
·
À partir de l’automne 2006 : École
mathématique pour musiciens et autres non-mathématiciens [dir. Y. André, F. Nicolas]
Les 32 interventions du séminaire mamuphi durant la période 2005-2007
|
|
Théorie de la musique avec les mathématiques |
Maths |
Philo |
||||
|
I Application |
II Mathématisation |
III Expérimentation |
|||||
|
2005 |
février |
C. Alunni |
|
|
|
|
|
|
M. Andreatta |
|
|
|
|
|
||
|
F. Nicolas |
|
|
|
|
|
||
|
mars |
Y. Hellegouarch |
|
|
|
|
|
|
|
M. Broué |
|
|
|
|
|
||
|
avril |
F. Nicolas |
|
|
|
|
|
|
|
G. Mazzola |
|
|
|
|
|
||
|
mai |
R. Guitart |
|
|
|
|
|
|
|
T. Paul |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
octobre |
F. Nicolas |
|
|
|
|
|
|
|
G. Mazzola |
|
|
|
|
|
||
|
novembre |
J.-Y. Girard |
|
|
|
|
|
|
|
décembre |
Y. André |
|
|
|
|
|
|
|
2006 |
janvier |
R. Guitart |
|
|
|
|
|
|
février |
P. Cartier |
|
|
|
|
|
|
|
mars |
J.-B. Joinet |
|
|
|
|
|
|
|
avril |
G. Longo |
|
|
|
|
|
|
|
mai |
G. Gargani |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
octobre |
F. Nicolas |
|
|
|
|
|
|
|
novembre |
M. Andreattta |
|
|
|
|
|
|
|
décembre |
R. Guitart |
|
|
|
|
|
|
|
2007 |
janvier |
S. Dugowson |
|
|
|
|
|
|
février |
D. Rabouin |
|
|
|
|
|
|
|
mars |
G. Dowek |
|
|
|
|
|
|
|
mai |
F. Nicolas |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
octobre |
M. Andreatta |
|
|
|
|
|
|
|
F. Nicolas |
|
|
|
|
|
||
|
C. Alunni |
|
|
|
|
|
||
|
novembre |
S. Schaub |
|
|
|
|
|
|
|
F. Nicolas |
|
|
|
|
|
||
|
décembre |
F. Borceux |
|
|
|
|
|
|
|
décembre |
R. Kromer |
|
|
|
|
|
|
|
23 séances |
32 interventions |
5 |
4 |
8 |
10 |
5 |
|
|
17 |
15 |
||||||