Conjecturer en musique ?
François Nicolas (février 2007)
Le compte rendu par Jörg Wildeshaus du livre d’Yves André Une introduction aux motifs dans la Gazette des mathématiciens de janvier 2007 [1] attire notre attention sur le rôle stratégique joué dans cette théorie des motifs par un réseau serré de conjectures.
Dans l’Avant-propos de l’ouvrage référencé [2], son auteur indique que cette théorie relevait jusqu’à récemment d’une sorte de « science-fiction mathématique » [3] pour ne conquérir des « assises non conjecturales » que depuis peu, l’un des enjeux de son livre devenant de « hiérarchiser et mettre en valeur la cohérence et la complémentarité des nombreuses conjectures qui forment l’armature idéale au sein de laquelle continue de s’échafauder la théorie. » [4]
Un rapide survol de l’ouvrage relève que la quarantaine de conjectures qui y interviennent forment un réseau dont les dépendances et entrecroisements se trouvent résumés en quelques « tableaux synoptiques » tel celui-ci [5] :

Il se trouve que cette importance des conjectures avait été thématisée par Yves André lors de son intervention (décembre 2005) au séminaire mamuphi (Ens-Ircam) : il y avait présenté ce qu’il appelle « l’art des conjectures » [6], en particulier cet art de produire des « constellations de conjectures » qui orientent ces vastes programmes de travail constituant « les plans quinquennaux des mathématiques ».
Il ressort ce faisant que la mathématique pratique un double « art des conjectures » :
· l’un où une théorie, solidement assise, se trouve orientée par une conjecture « architectonique » (celle de Riemann, ou encore jusqu’à tout récemment [7] celle de Poincaré concernant les variétés de dimension 3…), fonctionnant alors comme une sorte de phare général qui fixe un but précis et globalement situé mais qu’on ne sait comment atteindre ;
· l’autre où cette fois les conjectures opèrent en groupe, en réseau hiérarchisé (celui par exemple de la théorie des motifs, mais aussi du programme de Langlands en théorie des nombres), en sorte alors de baliser tout un continent (ou un archipel) restant cependant (provisoirement) inatteignable.
Ces propositions fonctionnent, pour un musicien curieux de mathématiques, comme une incitation à s’interroger sur le statut éventuel de la conjecture en musique : y a-t-il quelque équivalent musical au rôle joué en mathématique par la conjecture ? S’il est vrai que musique et mathématiques ont en partage non pas de supposés objets communs (tels les nombres ou les figures) mais bien des soucis de même nature (un double souci, dirais-je : un souci d’écriture – penser « à la lettre » : la mathématique avec les x et y, la musique avec les notes - et un souci de logique – savoir « déduire » : démontrer mathématiquement / développer musicalement), peut-on dégager en musique quelque pratique analogue à celle de la conjecture en mathématique ?
Voilà ce que je me propose d’examiner ici, pour le plaisir – je l’espère – du mathématicien curieux de musique…
1. Conjectures mathématiques
1.1. Quatre propriétés de la conjecture
Suivant en cela le point de vue exposé par Yves André tout en l’ajustant à ma cible propre, je caractériserai une conjecture mathématique par quatre propriétés :
1. Une propriété formelle : une conjecture est un énoncé susceptible de devenir tel quel un théorème. C’est donc un énoncé dont la forme est aussi précise et complète que celle d’un théorème. Une conjecture n’est pas une question, une affirmation vague ou une simple hypothèse.
2. Une motivation par l’amont : une conjecture, quoique non déduite (non démontrée, non prouvée), doit cependant être motivée par une mise en situation qui en relève la place charnière, la fonction carrefour, qui la rehausse comme cible de différentes tentatives. Une conjecture n’est pas une simple devinette, ou une curiosité isolée ; elle ne relève ni du concours Lépine, ni de l’almanach Vermot.
3. Une motivation par l’aval : une conjecture est motivée par sa portée, par ses conséquences, par les nouveaux énoncés qui peuvent s’y arrimer déductivement. Une conjecture n’est pas envisagée comme un cul-de-sac mais comme un nouveau point de départ possible. Elle ne relève pas de la rubrique « récréation mathématique ».
4. Enfin une dimension subjective d’orientation : une conjecture est un pari autorisé (elle engage un nom propre, doté d’une autorité : « conjecture de X ou Y »). Une conjecture n’est pas un jeu sans enjeu, une spéculation n’engageant qu’un joyeux illuminé.
Une conjecture mathématique a donc la forme exacte d’un théorème, énoncé doublement motivé et apte à orienter une recherche, mais restant non démontré. Le destin « naturel » d’un énoncé conjectural est alors de devenir, tel quel et sans aucun changement, un théorème.
1.2. Deux types de conjectures
Sur cette base, je distinguerai - comme indiqué précédemment - deux types de conjectures :
· la conjecture-phare, ou conjecture isolée, venant préciser un but qu’on ne sait atteindre (un énoncé qu’on ne sait démontrer) ;
· la constellation de conjectures, ou réseau de conjectures, configurant au loin la structure d’un continent qui reste inaccessible (selon les lois propres de l’accès mathématique).
1.3. Raisonances [8] en musique ?
Il s’agit, à partir de là, de se demander si la musique connaît, d’une manière restant à préciser, ce type de conjectures.
1.3.1 Deux questions mises de côté
Je laisserai ce faisant de côté deux questions :
1) celle de savoir si les conjectures mathématiques existantes ont des projections musicales envisageables. Je ne m’intéresserai donc pas ici à l’éventuelle portée musicale de telle ou telle conjecture mathématique mais seulement à l’art mathématique de conjecturer pour me demander : existe-t-il quelque art musical équivalent ?
2) Je n’examinerai pas non plus la question de savoir si la musique fournit (peut fournir, a déjà fourni…) à la mathématique l’occasion de conjectures [9]. Il ne s’agit donc pas ici d’interroger l’aptitude de la mathématique à théoriser la musique, en particulier sa capacité d’orienter les théories mathématiques de la musique par quelque conjecture (mathématique). Il s’agit plutôt de déceler l’existence éventuelle de « conjectures » en musique et non plus en mathématiques.
1.3.2 Distinguer le musicien du musical
Il est pour cela nécessaire de soigneusement distinguer en musique deux types de « discours » : le discours musicien (ou discours du musicien : celui par exemple que je suis en train de soutenir ici, et qui se déploie dans la langue vernaculaire commune aux êtres parlants) et le discours musical (ou discours de l’œuvre musicale qui, lui, se mène à l’écart des mots : selon une dialectique singulière des sons et des notes).
D’où deux questions bien distinctes :
1) Existe-t-il des conjectures musiciennes (ou quelque équivalent) ?
2) Existe-t-il des conjectures musicales (ou quelque équivalent) ?
2. Conjectures musiciennes
Peut-on d’abord isoler, dans le discours des musiciens, quelques énoncés prenant la forme soit de conjectures-phares, soit de constellations conjecturales ?
La réponse me semble clairement un double oui.
Voici à ce titre quelques exemples, prélevés - comme il convient (la quatrième caractéristique d’une conjecture est de constituer un pari doté d’une autorité) - dans les écrits de grands compositeurs.
2.1. Conjectures-phares
2.1.1 Schoenberg
En 1911, Arnold Schoenberg conclut son Traité d’harmonie [10] par une page fameuse conjecturant l’existence de la « mélodie de timbre » ou Klangfarbenmelodie :
« S’il est possible maintenant, à partir de timbres différenciés par la hauteur, de faire naître des figures sonores que l’on nomme mélodies — successions de sons dont la cohérence même suscite l’effet d’une idée — alors il doit être également possible, à partir de pures couleurs sonores — les timbres — de produire ainsi des successions de sons dont le rapport entre eux agit avec une logique en tout point équivalente à celle qui suffit à notre plaisir dans une simple mélodie de hauteurs. Il semblerait que cela soit une fantaisie futuriste, et c’est sans doute le cas. Mais une fantaisie dont j’ai la ferme conviction qu’elle se réalisera. »
Point remarquable (qui relève que cette « conjecture » était bien un pari de son auteur) : deux ans plus tard, en 1913, Schoenberg validera musicalement cette conjecture musicienne dans sa troisième pièce de son opus 16 intitulée Farben :

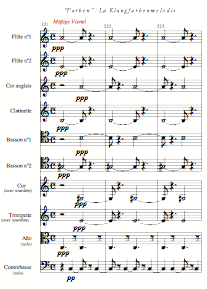
On voit qu’un accord stable se trouve ici « pulsé » selon deux couleurs orchestrales différentes formant « mélodie de timbres ».
2.1.2 Boulez
Deuxième exemple, moins connu, prélevé cette fois dans la correspondance Pierre Boulez / André Schaeffner [11]. Le 24 novembre 1961, Boulez écrit à Schaeffner ceci [12] :
« À propos des symphonies [d’instruments à vents de Stravinsky], juste un mot : je ne suis pas d’accord sur le côté pastoral que vous attribuez au passage pour flûte et clarinette ; j’y vois plutôt la continuation de la liturgie ; mais par rapport au thrène aigu modulé au début, il s’agit tout à coup d’une liturgie basse, et je voudrais toujours rendre ce passage comme, par exemple, ce dialogue marmonné à voix basse entre le prêtre et son enfant de chœur lors d’une messe basse ; ou encore ces marmonnements du vieillard initiant, en attendant la transe et le paroxysme, et qui ronronne son petit jus jusqu’à ce qu’arrive le déchaînement ; ou encore comme le violon chinois dans le théâtre traditionnel : après les pires cataclysmes, où cymbales et cris se sont déchaînés, on entend émerger cet infime nasillement, témoin et garant de la continuité. J’aurais voulu rendre cela, mais ce n’est encore pas arrivé… probablement faudra-t-il que je l’écrive moi-même dans une œuvre pour y arriver. »
Boulez formule ici une « conjecture » quant au passage suivant de la Symphonie d’instruments à vents (1920, révisée en 1947) [13]

conjecture qu’on pourrait dire de simple interprétation (« comment comprendre ce passage et par là le rendre ? ») mais qui s’avère de portée plus vaste puisqu’elle débouche, comme la précédente de Schoenberg, sur une perspective compositionnelle : Boulez conclut en effet en suggérant que l’idée musicale dégagée sera mieux validée par une création compositionnelle, ce qu’il réalisera, effectivement, trois années plus tard (comme Schoenberg à nouveau), en ajoutant à son œuvre Doubles le passage suivant [14], précisément annoté « Violon chinois » dans ses esquisses [15], apport qui, joint à d’autres, débouchera sur une nouvelle œuvre Figures Doubles Prismes :

2.1.3 « Conjectures »
Dans ces deux cas, les énoncés du musicien correspondent, bonens volans, aux quatre caractéristiques de la conjecture mathématique :
· Leur énonciation est aussi bien formée que la langue du musicien le permet en matière de musique.
· Les propositions ainsi faites sont motivées - sans doute en amont (celle de Schoenberg conclut ainsi son vaste ouvrage) plus qu’en aval (encore que Schoenberg suggère la grande portée de la Klangfarbenmelodie) -.
· Les deux engagent leur auteur – qui au demeurant sont des acteurs centraux de la scène musicale - comme en atteste ce que l’un et l’autre composeront quelques années plus tard.
Dans les deux cas, ces énoncés orientent bien le travail musicien à la manière dont le phare conjectural peut le faire en mathématique.
2.2. Programmes conjecturaux
Qu’en est-il cette fois, dans le discours musicien, d’éventuelles constellations de conjecture ?
2.2.1 Berlioz
Donnons ici l’exemple de Berlioz [16] qui conclut en 1844 son Traité d’instrumentation et d’orchestration par des considérations [17] minutieuses sur un futur « orchestre monumental », vaste « peuple musical » composé de 827 exécutants [18], « multitude de timbres différents » dont « il y aurait des effets harmoniques inouïs à tirer », par exemple ceux-ci, prélevés dans la vingtaine que Berlioz détaille :
· division en 8 ou 10 parties des 120 violons aidés des 40 altos, le tout en pianissimo dans l’aigu ;
· réunion des 30 harpes et de tous les instruments à archets en pizzicato en sorte de composer une « Harpe gigantesque à 934 cordes » ;
· réunion des 30 pianos, des 6 jeux de timbre, des 12 paires de cymbale, des 6 triangles et des 4 pavillons chinois en un orchestre à percussion métallique joué mƒ…
Berlioz n’eut pas vraiment le loisir de mettre en œuvre ce dispositif orchestral et il fallut donc attendre le XX° siècle (Varèse, Ligeti, etc.) pour entendre effectivement de tels ensembles de percussions, de telles masses de cordes pizzicato ou glissando, etc.
Relevons ce point remarquable : Berlioz inscrit cet orchestre « conjectural » sous la loi d’un axiome explicite : « la musique en plein air n’existe pas », énoncé qui prescrit qu’un tel orchestre agisse musicalement en un lieu fermé et non pas en « un vaste jardin ouvert de toutes parts, comme celui des Tuileries » puisque le son de cet orchestre doit se conformer aux lois essentielles du son musical lequel se distingue de n’importe quel son en particulier en ceci qu’il joue des réflexions sur les murs et cloisons. [19]
Cet « orchestre monumental », minutieusement profilé et soigneusement articulé en formations instrumentales mais non musicalement réalisé, occupe ainsi pour le musicien la place d’une constellation conjecturale : vaste continent-archipel dont la structure est dégagée tout en restant encore inatteinte.
2.3. Objection
Ces analogies en matière de conjectures musiciennes soulèvent cependant une objection immédiate : ne se trouve-t-on pas ici renvoyé à l’espace des sciences expérimentales plutôt qu’à celui de la mathématique proprement dite ? Les « conjectures musiciennes » ne sont-elles pas conjecturales en un sens dévié, qui renvoie à des expériences à venir, à des validations matérielles plutôt qu’à des déductions ? Ces suppositions musiciennes ne sont-elles pas l’équivalent d’hypothèses physiciennes plutôt que de conjectures mathématiques ?
La pointe de l’objection porte sur la nature même de ce qui fera validation ou non de l’énoncé ainsi interrogé : une expérience, dans le cas de l’hypothèse physique (expérience qui, à proprement parler, ne saurait rien prouver, mais tout au plus invalider le principe et amener donc le physicien à en préciser les conditions de validité), une démonstration dans le cas de la conjecture mathématique.
Or le discours du musicien ne procède guère par axiomes et déductions, et son intellectualité propre n’est pas à proprement parler démonstrative.
S’il nous faut chercher un équivalent musical de la démonstration mathématique – cette démonstration qui discrimine précisément un théorème d’une conjecture -, si l’on cherche une modalité de déduction musicale, il nous faut donc nous intéresser cette fois au « discours musical », soit ce discours à l’œuvre qui mobilise cette modalité proprement musicale de la déduction qu’on appelle « développement » (ou Durchführung).
3. Conjectures musicales
3.1. Formalisation du problème
Posons d’emblée nos hypothèses de travail pour ces « raisonances mathématiques→musique » en matière de conjectures.
3.1.1 Axiome, théorème, conjecture, devinette…
Quel équivalent musical trouver à la triple modalité d’énonciation axiome/théorème-conjecture ?
Adoptons pour cela la distinction formelle suivante (où l’amont d’un énoncé mathématique est sa démonstration et son aval ce que l’on en déduit) :
· Un axiome est un énoncé ayant toujours un aval mais, par principe, pas d’amont.
· Un théorème est un énoncé qui a toujours un amont, et le plus souvent un aval (sinon, appelons-le un théorème – provisoirement - terminal)
· Une conjecture est un énoncé qui n’a pas encore d’amont mais un aval (des conséquences conditionnées : « s’il est vrai que… alors… »).
· Une devinette mathématique est un énoncé sans amont et sans aval (sans conséquences) : un énoncé strictement isolé.
|
|
aval |
|||
|
oui |
non |
|||
|
amont |
oui |
théorème |
[théorème provisoirement terminal] |
|
|
non |
par principe |
axiome |
[élucubration !] |
|
|
de
facto |
conjecture |
devinette |
||
3.1.2 Thème, variation, mélodie…
L’équivalent, en matière d’énonciation musicale, serait alors le suivant [20] :
· Un thème est un énoncé musical ayant toujours un aval (un thème sans variation/altération n’est pas un thème) mais en principe sans amont dans l’œuvre où il agit (il n’est pas construit par l’œuvre en question mais y surgit).
· Une variation est un énoncé musical qui a toujours un amont, et le plus souvent un aval (sinon, appelons-la une variation conclusive)
· Une mélodie est un énoncé musical sans amont (elle surgit sans être construite) et sans aval (une mélodie se répète, avec quelques variantes certes mais sans être à proprement parler développée comme l’est, par nature, un thème [21]).
3.1.3 Et la conjecture ?
Reste alors notre question : y a-t-il un équivalent musical de la conjecture mathématique c’est-à-dire un énoncé susceptible d’avoir un amont (en l’état inexistant) et doté d’un aval (aval potentiel à tout le moins) ?
Soit le petit tableau suivant :
|
mathématique |
|
musicale |
|
axiomes |
|
thèmes |
|
théorèmes (éventuellement terminaux) |
|
variations (éventuellement conclusives) |
|
devinettes |
|
mélodies |
|
conjectures |
|
? |
Notre question est donc : existe-t-il, dans une grande œuvre musicale (4° caractéristique de la conjecture : elle est un pari sérieux et faisant autorité), un énoncé précisément formulé, qui à la fois ne procède pas du développement qui le précède et ne soit pas sans développement dans l’œuvre en question ?
3.1.4 Une réponse décevante…
Ainsi directement transposée de notre formalisation, cette question appelle une réponse simple mais décevante : n’importe quel thème musical dispose a priori de ces propriétés, et ceci en raison du fait qu’il n’est guère possible de distinguer en musique un axiome-thème d’un théorème-variation ; en effet, si on peut le faire dans une œuvre donnée (le thème se situe au début, les variations le suivent), par contre ce même thème liminaire peut parfaitement constituer la variation conclusive d’une autre œuvre.
3.1.5 Coconjecture / cothème
D’où la proposition suivante : la raisonance en musique de la conjecture mathématique se trouvera dans ce qu’on proposera d’appeler ici une coconjecture musicale c’est-à-dire une figure duale (dualité catégorielle : par inversion des flèches dans les rapports amont-aval précisés ci-dessus) de la conjecture mathématique :
|
Conjecture mathématique
|
Coconjecture musicale
|
3.1.5.1 Caractérisations du cothème
Pour cela, on appellera cothème un énoncé musical aux quatre propriétés suivantes :
1) il a la forme exacte d’un thème (il pourrait, tel quel, être un thème : ce n’est donc pas une mélodie, ou un simple motif) ;
2) il est motivé par l’œuvre : il y apparaît en cours de développement, non comme une digression, une citation ou un objet trouvé, mais bien comme une production sui generis ;
3) il n’est cependant pas varié comme il devrait musicalement l’être (s’il se répète dans l’œuvre en question, il le fera sans altération, comme le ferait une mélodie - qu’il n’est pas…) ;
4) il apparaît dans un chef d’œuvre musical, non dans une curiosité ou une élucubration musicale.
On se demandera, sur cette base :
· Existe-t-il de tels cothèmes isolés, sorte de cophares (trous noirs ?) ?
· Existe-t-il des constellations de tels cothèmes, sorte de gouffres circonscrits ?
3.1.5.2 Fonction désorientante !
Ceci suggère que de tels éventuels cothèmes (isolés ou en réseau) auraient alors dans l’œuvre musicale une fonction cette fois désorientante : au lieu d’un « art mathématique de conjecturer pour s’orienter », il s’agirait de repérer « un savoir musical coconjecturer pour désorienter l’audition et ainsi (r)éveiller l’écoute » [22].
3.1.5.3 Dualité mathématiques/musique
Au total, on résumera cette dualité dans le tableau suivant :
|
|
Conjecture
mathématique |
Coconjecture
musicale: le
cothème |
||
|
Formulation |
|
Forme d’un théorème |
Forme d’un thème |
|
|
a
contrario |
Question, hypothèse… |
Mélodie, motif… |
||
|
Déduction |
en amont |
|
Non (énoncé non démontré) |
Oui (énoncé engendré) |
|
a contrario |
Devinette, curiosité |
Objet trouvé, citation… |
||
|
en aval |
|
Oui (on démontre à partir de lui) |
Non (énoncé non développé) |
|
|
a contrario |
Récréation |
Thème |
||
|
Pari |
|
relève d’un auteur engageant son autorité |
proposé par un chef d’œuvre |
|
|
a contrario |
spéculation d’illuminé ou de farfelu… |
dans une pièce de musique expérimentale ou un jeu musical… |
||
|
Logique |
d’orientation |
de
désorientation |
||
3.2. Coconjectures musicales isolées
3.2.1 Beethoven
Donnons un exemple canonique de thème sans développement. Il s’agit du « troisième » thème apparaissant en plein développement du premier mouvement de l’Héroïque (troisième symphonie), en une position donc tout à fait inhabituelle (sans équivalent, à vrai dire, dans toute l’histoire de la Forme-Sonate) car à la fois :
· surnéméraire (la Forme-Sonate est intrinsèquement bithématique),
· inattendu en cours de développement (donc en-dehors des moments d’exposition et réexposition)
· et inutilisé comme thème (c’est-à-dire non développé à l’égal des deux autres).
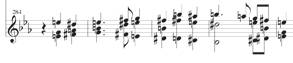
3.2.2 Un autre cas de figure…
Voici un autre cas de figure, candidat à la posture de coconjecture, illustré cette fois par deux compositions différentes.
3.2.2.1 Franz Liszt
Dans sa Fantaisie et fugue pour orgue sur « Ad nos, ad salutarem undam » (1850), l’ensemble du thème (choral hérité) qui se trouve au principe de la construction n’est restitué qu’à la fin de l’œuvre – selon une harmonisation monumentale - si bien que ce sont les variations qui semblent délivrer ultimement leur origine effective :

3.2.2.2 César Franck
Dans son premier choral pour orgue (1890), Franck opère de même, en apothéose triomphale, avec pour pas supplémentaire le fait qu’ici le thème n’est pas hérité mais « se fait au cours même de l’œuvre » :

Dans ces deux cas, l’ordre canonique thème→variations (identité→altérations) est traité de manière rétrograde (la rétrogradation musicale est une modalité possible de la dualité catégoricienne qui inverse le sens des flèches) si bien que le thème apparaît ultimement en quasi-position de cothème.
3.3. Réseau de coconjectures musicales
3.3.1 Wagner
Cette logique coconjecturale peut même prendre un tour de quasi constellation avec Wagner.
Si l’on examine ainsi le réseau des leitmotive d’un opéra de Wagner, on peut en effet y constater l’existence – rare - de thèmes inactifs, c’est-à-dire à proprement parler non variés, non altérés.
Voici par exemple une présentation possible du réseau des 36 leitmotive canoniquement distingués dans Parsifal :
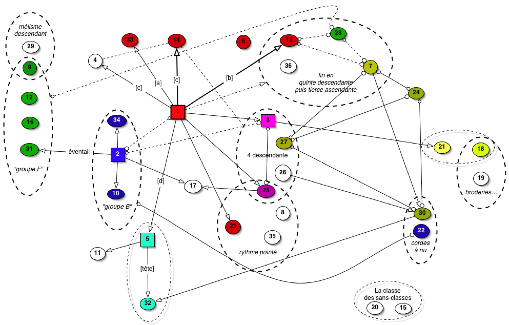
Un leimotiv wagnérien, plus encore qu’un thème musical habituel, est moins une forme particulière donnée qu’une capacité singulière de se former/déformer, qu’une aptitude singulière à la dé/formation donc. À ce titre, classer les leitmotivs (les distinguer, les relier en familles, etc.) ressemble beaucoup à l’activité néphologique consistant à classer les nuages ce qui, depuis Luke Howard [23], se fait moins par la statique des formes que par la dynamique de leurs évolutions.
L’existence de leitmotivs isolés (séparés du réseau et n’interagissant guère avec lui : ici les n° 15, 20) et surtout de leitmotivs ne remplissant pas leur fonction thématique (altération-déformation) tout en disposant de toutes les caractéristiques formelles d’un thème wagnérien (ici les n°29 et 36 [24]) préfigure alors un réseau possible (non présenté comme tel par l’opéra) de « cothèmes » [25].
Ainsi les leitmotivs numérotés 29 (dit de la tentation) et 36 (dit de l’offrande expiatoire) n’interviennent chacun que deux fois [26] et à l’identique dans tout l’opéra :
![]()

L’opéra conjecture implicitement (coconjecture…) que ces leitmotivs auraient tout aussi bien pu opérer à l’égal des autres : comme foyers de déformations et mutations, bref comme thèmes au sens particulier que Wagner donnait à cette catégorie.
*