Théorie des catégories, théorie des topos
Alain Badiou (1995-1996)
[Notes de Daniel Fischer]
1. Introduction 2
2. La querelle
autour de l'axiome du choix 3
3. Le thème contemporain de la finitude 4
4. Construction catégorielle de l'axiome du choix 6
a) 6
Différenciation logique de l'axiome du choix 8
4.1 8
NOTE ADDITIONNELLE SUR LA DIFFÉRENCE 9
b) 11
démonstration.................................................................................................................... 12
4.2 12
4.3 13
5 Qu'est-ce que le classicisme en Théorie des Topos ? 15
Voyons pour commencer où nous en étions arrivés à la fin de l'année dernière. L'idée centrale c'est que des contraintes formelles nouent entre eux ce que j'ai appelé les cinq concepts fondamentaux de l'onto-logie : la décision, le vide, la négation, la différence et l'infini. Ces contraintes formelles sont exprimées dans des théorèmes qui constituent l'armature logique de toute décision ontologique.
Ces théorèmes nous permettent de penser l'idée fondamentale suivante : la logique rétroactivement instituée par une décision est le prix à payer pour une liberté. En ce sens, être véritablement libre c'est en réalité être conséquent avec un principe. Dans mes termes : toute liberté est une fidélité (à un événement). C'est là le sens de la formule de Mallarmé : "le hasard vaincu mot par mot".
Deux de ces théorèmes ont fait l'objet d'une démonstration. J'en redonne l'énoncé :
1. Tout
Topos qui admet un opérateur de succession en position universelle admet un objet
intrinsèquement infini.
Autrement dit : un Topos qui admet le concept de l'infini comme récurrence ou itération indéfinie (i.e. l'infini potentiel) admet aussi une détermination intrinsèque de l'infini (i.e. l'infini actuel). Plus exactement : un Topos qui admet le premier type d'infini est contraint d'admettre le second. L'infini conçu comme itération indéfinie n'est par conséquent pas une limitation, car on ne saurait penser, dans une sorte d'entre-deux prudent, un statut autonome de l'indéfini; ultimement, la décision ontologique consiste soit à admettre qu'il y a de l'infini soit à le refuser.
2. Si dans un Topos il y a unicité du vide
et que la logique du Topos est classique, alors le Topos est bien pointé.
Ce que nous avons en réalité démontré l'année dernière, c'est la réciproque de ce théorème, à savoir que, dans un Topos bien pointé, il y a unicité du vide et que la logique à laquelle ce Topos obéit est nécessairement une logique classique (la démonstration de l'énoncé direct est, quant à elle, particulièrement aride).
On peut formuler ce théorème de
la façon suivante : s'il y a du Zéro (Zéro étant le nom générique du vide
comme unique) et que le Deux est central (par où s'exprime le
caractère classique de la négation : force maximale de la disjonction p ou ~ p -
principe du tiers exclu - et atténuation de la force créatrice de la négation -
équivalence de p et de la double négation de p), alors il y a de l'Un dans la différence (différence extensionnelle où l'on
conclut à la différence entre deux ensembles par la monstration d'un
élément qui entre dans la présentation de l'un et non dans celle de l'autre).
On peut d'ailleurs se demander si toute
décision ontologique dans la pensée n'est pas toujours un régime particulier de
connexion entre Zéro, Un et Deux ...
Abordons donc le 3ème théorème,
qui fait noeud de la décision et de la négation.
Théorème 3 :
tout Topos qui admet l'axiome du choix est classique (théorème de Diaconescu : 1975).
1. Introduction
Il y a des théories de la décision qui supposent, pour toute décision, une réduction au fini de son espace d'exercice; autrement dit : tant que la situation est proprement infinie, la décision est considérée par ces théories comme impraticable ou arbitraire. Une fois la situation ramenée à sa finitude, préalable nécessaire à toute décision rationnelle, elle pourra le cas échéant être déclarée "complexe" et même à un point tel que toute décision concrète s'y révèlera en réalité impossible - on aura reconnu là une thèse majeure du monde contemporain. Or, l'axiome du choix énonce qu'on peut décider dans l'infini[1]. D'où les controverses auxquelles il a donné lieu et qui sont loin d'être éteintes aujourd'hui.
Notre théorème pourra par conséquent se formuler ainsi : si dans votre univers vous admettez la décision infinie, alors la logique de cet univers est nécessairement classique : toute décision y est sous la loi d'un Deux en disjonction effective (soumis au principe du tiers exclu); vous ne pouvez plus être dans le modal quant à la négation (le monde des situations "complexes" est un monde de la modalité), la position centriste est intenable.
La décision ontologique établit donc, avec ce théorème, une connexion entre l'infini et le Deux, connexion qui, il faut le reconnaître, n'est pas immédiatement perceptible[2].
Nous avons vu l'année dernière que les logiques non classiques, dans lesquelles il n'est pas vrai que ~~p p, impliquent à la fois une atténuation de la force disjonctive de la négation et une réelle force créatrice de celle-ci - partant elles impliquent une topologie qui n'est pas triviale comme dans les logiques classiques, mais une authentique création d'espace, une topologie des voisinages. Par conséquent, notre théorème s'exprime également de la façon suivante : si vous admettez la décision infinie, alors votre univers, en tant qu'il est contraint au classicisme, n'est pas compatible avec un fonctionnement topologique.
La logique hégélienne est un exemple typique de logique non classique.
Comme vous le savez, toute différence est, pour Hegel, ce que le négatif qui est au coeur de l'être fait surgir comme expression de lui-même. Mais la négation n'est pas seulement au coeur de l'être, elle doit d'une certaine manière y revenir : la négation va se projeter dans des différences concrètes, des figures, puis ces figures vont retourner, ou se réinjecter, dans leur origine de telle sorte que la négation va elle-même être niée. C'est le thème, fondamental chez Hegel, de la négation de la négation comme moment de la vérité. Autrement dit : la vérité d'une chose, c'est son devenir, i.e. le travail en elle du négatif; mais pour faire vérité de ce devenir, il faut que le devenir rentre en lui-même comme conscience de soi, il faut donc qu'il y ait en quelque sorte un devenir du devenir, c'est-à-dire effectivement une négation de la négation. Le retour à l'immédiat de p, une fois que p a été deux fois nié, produit autre chose que p, mais aussi le principe d'intelligibilité de l'immédiat lui-même : p peut alors être dit conscient de lui-même. La double négation est chez Hegel à la fois création (avènement d'une nouvelle figure) et retour (ce qui rend raison de son origine).
Revenant à notre théorème, nous
pouvons donc énoncer que la possibilité de la décision infinie est
incompatible avec la dialectique; et réciproquement : si la double négation est créatrice,
alors la décision infinie est impossible.
On comprend que ceci a pu embarrasser les marxistes. Car la question est la suivante : où est la capacité créatrice, par où le nouveau advient-il ? Est-ce au travers de la négativité elle-même (le "travail du négatif") ? On a alors affaire à la figure dialectique hégélienne (et en fait, plus lointainement, à Héraclite). Ou bien la création est-elle une figure d'extension à l'infini de la décision, ce que j'ai appelé la décision infinie ? - ce qui suppose, pour que le nouveau puisse advenir, que la décision comporte nécessairement (c'est l'axiome du choix qui nous l'apprend) une part de pari, implique que quelque chose soit gagé sans aucun calcul. Or, le théorème nous apprend qu'il y a incompatibilité entre ces deux figures. Soit vous êtes l'homme des trajets topologiques et vous déclarerez que les choses suivent leur cours au travers du travail du négatif, moyennant certains ajustements à imprimer à ce cours; vous serez alors immanquablement amené à prononcer, dans une situation que d'aucuns jugeraient "pré-révolutionnaire", que les paramètres ne sont pas (encore) réunis pour la qualifier comme telle et qu'il faut (encore) attendre. Soit, tenant de l'autre figure, vous poserez qu'une décision est nécessaire sans que l'on puisse être dans l'assurance d'une connaissance adéquate de la topologie du système (car dans une situation infinie il y a toujours la possibilité qu'il y ait des paramètres incontrolés) et qu'au contraire, pour reprendre les termes de J.C. Milner, il est possible "qu'un geste puisse créer les conditions qui, rétroactivement, le font juste et opportun" (J.C. Milner Les noms indistincts p. 16 note 3). Il y a là-dessus un texte extraordinaire de Lénine datant de l'automne 1917 : La crise est mûre. Il y expose, à l'intention des dirigeants du Comité Central, pour qui la force des bolchéviks c'est d'attendre, que les conditions pour déclencher l'insurrection sont désormais réunies : il se place de ce fait dans une logique hégéliano-marxiste. Mais il ajoute, dans le même texte, que de toute façon, et en quelque sorte indépendamment des propriétés cumulables liées à ces circonstances objectives, il faut y aller : cette fois-ci il est dans la position où il assume l'axiome du choix (cf. Théorie du sujet p. 187-188 et S. Lazarus : "La politique n'est historique que rétrospectivement, au simple titre qu'elle a eu lieu (...) La période de la prise de pouvoir est décisive parce que c'est une période où la myopie historique de la politique est attestée, où ses intrications à l'histoire réelle sont les plus fortes et les plus grandes" (Lénine et le temps p. 23-24)).
2. La querelle autour de l'axiome du choix
Supposons une collection infinie d'ensembles disjoints non vides A1, A2, ..., Ai. L'axiome du choix pose qu'il existe alors toujours un ensemble composé en prenant un élément, et un seul, de chacun des ensembles disjoints. Cet ensemble, composé par conséquent de "représentants" des différents Ai de la collection initiale, est appelé l'ensemble-choix. Autrement dit : dans une situation infinie, existe une représentation, elle-même infinie, selon l'Un (car chaque ensemble est représenté par un élément et un seul).
L'axiome du choix est un axiome existentiel, il pose l'existence de l'ensemble-choix. On peut dire aussi que ce dont l'existence est affirmée c'est une fonction - la fonction de choix fc - qui, à chacun des ensembles A1, A2,... de la collection initiale, fait correspondre un de ses éléments :
( fc) ( Ai) ( xi) xi Ai et fc(Ai) = xi
Le point essentiel est que si la collection est infinie, la règle selon laquelle les choix s'opèrent n'est pas explicitement définie : "en ce sens, la fonction de choix est essentiellement illégale au regard de ce qui prescrit qu'un multiple puisse être déclaré existant" (EE p. 251); on démontre même que, si la suite des ensembles initiaux est infinie, l'ensemble-choix n'est pas définissable, i.e. qu'il n'est constructible par aucune formule explicite. On ne sait pas "qui" sont les représentants, comment ils sont selectionnés dans l'ensemble auquel ils appartiennent, on sait seulement qu'il y en a un, mais c'est n'importe qui : "ce représentant n'a pas d'autre identité que d'avoir à représenter le multiple auquel il appartient. Illégale, la représentation par choix est tout aussi bien anonyme" (EE p. 253).
L'axiome du choix est une décision sur les puissances de la décision, c'est une décision sur la décision car on atteint ici un degré de non-constructibilité radicale. C'est précisément ce qui fait le fond de la querelle autour de l'axiome du choix, querelle qui est avant tout de nature philosophique, car les grands analystes français de la fin du siècle dernier en faisaient implicitement usage dans leurs propres démonstrations; c'est son explicitation formelle qui leur parut excéder absolument ce qu'ils acceptaient quant au maniement de l'infini. Et surtout la controverse portait sur la question de savoir s'il est ou non acceptable d'étendre le régime de la décision au degré où le fait l'axiome du choix (puisque celui-ci énonce que le caractère infini de la situation ne fait pas obstacle au principe qui consiste à injecter de l'Un dans le multiple d'une situation).
C'est très précisément sur ce point que l'acceptation de l'axiome du choix a suscité, et ce très tôt, des objections. Bettazi, un mathématicien italien de l'école de Peano, les a énoncées explicitement dès 1892 : il est impossible qu'une traversée de l'infini saisisse à chaque fois un seul point. Le mathématicien français Borel a formulé la même objection dans les termes suivants en 1908 : l'axiome du choix consiste en une suite infinie de choix arbitraires. Il entendait signifier par là que, de l'existence affirmée par l'axiome, nous ne comprenons que le résultat mais pas le mode opératoire de l'opération qui a conduit à ce résultat. L'axiome du choix est inconstructible. Il y a certes choix, mais comment on choisit - ou plutôt comment ça choisit - nul ne le sait; comme s'il y avait là un inconscient opératoire inaccessible, dont nous n'aurions que le résultat - ou le symptôme; comme si nous avions affaire à un lapsus - mais sans théorie du lapsus. L'insupportable est en définitive qu'il y a là du sans-raison, qui cependant opère. La "consolation" trouvée par Borel résidait en ce que le prélèvement d'un point dans une série infinie d'ensembles, en quoi consistent les choix de l'axiome, est néanmoins revêtu d'un sens, même précaire ou approché, si je peux y introduire une clause de finitude : si la série est infinie, mais que cet infini est dénombrable, j'ai au moins la consolation de savoir que chaque choix n'est obtenu qu'au bout d'un temps fini.
Ce que nous apportera l'approche catégorielle de l'axiome du choix, c'est d'abord que l'univers des catégories n'est pas un univers décidé : cette approche considère, nous l'avons dit à plusieurs reprises, les univers possibles. Le sens n'y est pas envisagé de façon absolue, mais est toujours rapporté à un univers particulier : un énoncé ne reçoit une interprétation que dans un Topos donné. Autrement dit : l'assignation du sens dépend de l'univers choisi. La question catégorielle n'est donc pas : "l'axiome du choix a-t-il un sens ?" mais celle-ci : "dans quel type d'univers l'axiome du choix est-il possible ?" ou encore : "quelle est la forme logique d'un univers tel que la corrélation singulière de l'Un et de l'infini, en quoi consiste l'axiome du choix, y aura été décidée?"
3. Le thème contemporain de la finitude
Le principe de finitude est, vous le savez, essentiel à la philosophie contemporaine. Mais il faut en prendre précisément la mesure : il ne s'agit pas tant ici, en effet, de savoir si ce qu'il y a est fini, i.e. en fin de compte du rappel à l'homme de sa condition mortelle, que de la pensée de la convocation au fini de l'être-là de l'homme (pour user d'une terminologie heideggerienne). "Fini" sera donc à entendre simultanément en deux sens : ce qui a rapport à une fin (au sens du finir) et ce qui est dans l'exposition de sa limite.
Kant peut en ce cas être considéré comme le premier penseur de la finitude, par l'accent qu'il a mis sur le caractère fini de la connaissance, celle-ci ne pouvant être désormais appréhendée que selon le principe de sa limite. Ce n'est pas par hasard si c'est dans le livre que Heidegger a consacré à Kant que l'on trouve la maxime suivante : "L'élaboration de l'essence la plus intime de la finitude doit toujours elle-même de manière principielle être finie", maxime qui est centrale dans ce que je considère comme le traité contemporain le plus systématique de la finitude (en dépit des dénégations de son auteur quant à ce caractère de traité), à savoir Une pensée finie de J.L. Nancy. Celui-ci établit que la question de la finitude s'impose au point où finit un registre du sens antérieurement opératoire[3]. Puisque les catégories de Dieu, d'Homme, d'Histoire, de Sujet, ... en sont venues à défaillir, la tâche qui nous incombe est celle "d'une pensée à hauteur de fin" (p. 12). Il s'agit de décliner une pensée finie dans la finitude du sens - d'où la signification que le terme de "finitude" prend chez Nancy : celle d'une existence conçue comme sans essence, sans fondement. Le "sans-essence de l'exister", c'est en effet pour lui l'exister soustrait à lui-même comme sens.
On comprend que dans un tel cadre une décision au regard de l'infini serait proprement exorbitante; elle outrepasserait la ressource (pour nous épuisée) du sens, elle ne nous serait plus contemporaine; en un mot : elle serait métaphysique en son principe.
Dans le débat que j'entretiens avec J.L. Nancy, je voudrais dire ceci : son dispositif suppose qu'il y ait eu naufrage du sens et convoque à cette fin une historialité posée de façon dramatique (la catastrophe nazie ...). Or je n'entérine aucunement que quelque chose comme un "naufrage du sens" ait eu lieu; ma position est que cet événement est construit et que le retrait du sens est en fait entamé depuis toujours et en outre depuis toujours proclamé - proclamation qui, également depuis toujours, s'accompagne de la promesse d'un Retour. A l'époque de l'épuisement de la métaphysique, Heidegger affirme, reprenant le thème à Hölderlin, "Seul un Dieu peut nous sauver" - le mot "Dieu" désignant ici "la venue sans concept d'un retournement salvateur" (Conditions p. 58). Mais c'est de toujours qu'il a été dit : il y a une fin du monde et il faut que le monde revienne. Le couplage de la perte et de la promesse du comblement de cette perte est ce qui constitue le sens lui-même (dont Lacan avait bien raison de dire qu'il est intrinsèquement religieux) et c'est pourquoi il ne saurait y avoir de "naufrage du sens" (sinon qu'à faire naufrage, c'est le sens même du sens qui alors advient) : de toujours le sens est perdu, et le sens c'est cela même. Il n'y a que le Capital qui soit un fauteur général de perte du sens sans être en même temps dans la prétention à identifier un sens à venir dans la forme d'une donation - c'est là sa laïcité intégrale, impeccablement reconnue par Marx, qui créditait le Capital d'être le "dissolvant général des représentations sacralisantes" (cf. Manifeste pour la philosophie p. 36), lui qui "a noyé les frissons sacrés de l'extase religieuse, de l'enthousiasme chevaleresque, de la sentimentalité petite-bourgeoise dans les eaux glacées du calcul égoïste"; ce même Marx qui a épinglé du terme de "socialisme féodal" le voeu d'une restitution du sens, d'une réactivation du sens au point de sa perte (c'est une réactivation au sens où l'entendait Nietzsche qu'il faut ici comprendre). Plutôt qu'une "pensée à hauteur de fin", qui nous expose en fin de compte à un retour des vieux dieux, supports d'une pensée du sens (retour effectif : les nations, les ethnies, etc.), c'est une pensée à hauteur de Capital qu'il nous faut.
Pour J.L. Nancy si la finitude est notre lot, l'infini de l'Être est exposé comme sens. Or selon moi, l'Être doit être au contraire pensé comme une multiplicité insensée (et très exactement : in-sensée - le trait d'union désigne ceci que l'Être ne relève en aucune façon de la question du sens), multiplicité infinie qui en outre, parce qu'elle est une multiplicité inconsistante, ne fait pas Un - c'est la version que, quant à moi, je propose du thème nietzschéen de la "mort de Dieu" : l'infini ne fait pas Un[4]. Dans ces conditions comment l'Un opère-t-il dans l'axiome du choix ? Au lieu de dire que "l'Un est", ce qui renverrait à une donation de sens, je propose une interprétation particulière de la formule "il y a de l'Un". Il s'agit d'une opération de traversée de l'infini telle que la trace de la traversée soit à chaque fois sous le signe de l'Un, une trouée mais sans totalisation; de l'Un est extorqué à l'infini par le tracé d'une traverse. Je dirai qu'il n'y a d'Un qu'en traverse de la multiplicité infinie, mais sans qu'elle soit scellée, sans qu'elle soit recollectée : si l'Un est, il n'est que de travers et cette traversée est liée à une décision.
La réponse que fournit J.L. Nancy dans son livre à la question : "qu'est-ce qu'une décision de pensée ?" est ici du plus haut intérêt. La décision est, selon lui, "l'objet indécidable par excellence", tout en étant "appropriation d'elle-même" (p. 111). Je souscrirais volontiers à la première formule (en émettant cependant des réserves sur le mot "objet") : la décision qui prend la forme d'un énoncé purement existentiel ("il existe ...") touche à l'in-fondé, car l'exister est précisément ce qui est sans essence, ce qui est sans fondement; la décision se meut donc nécessairement dans l'élément de l'indécidable. La deuxième formule, quant à elle, pose que la décision est dans l'exposition à sa propre limite et, par là, réintroduit le thème de la finitude avec lequel je suis en foncier désaccord. Le caractère existentiel de l'axiome du choix supporte, pour J.L. Nancy, le fait que la figure de l'exister pur exposé à la perte du sens puisse attester quand même, dans l'élément de la finitude, de la venue d'un sens. Il reconduit par là un dispositif qui, à mon avis, est en fin de compte chrétien : le christianisme est en effet fondamentalement l'expérience d'une finitude de Dieu, finitude qui est relevée par une opération du sens au point de la perte absolue de celui-ci. Quand Jésus sur la croix prononce "Mon Père, pourquoi m'as-tu abandonné ?", la perte du sens est à son comble, c'est le sens lui-même qui est crucifié - mais pour être relevé : dans un exister. Le christianisme est une religion de l'existence.
Je soutiens au contraire que le caractère existentiel de l'axiome du choix témoigne d'une décision d'existence qui prend sur elle la dimension de l'in-sensé. J'en vois le symptôme dans ceci que l'axiome comporte très peu de définitions de ce dont il affirme l'existence, ce qui a intimement à voir avec son caractère inconstructible. Comme nous le verrons plus tard, l'axiome du choix, en véritable caméléon, se donne dans une grande variété d'énoncés d'allures très diverses, énoncés dont l'équivalence est elle-même difficilement perceptible; ce qu'il pense est en réalité délié d'un énoncé particulier, il est un dire plutôt qu'un dit. L'axiome lui-même est ce dire, déposé dans tel ou tel dit.
4. Construction catégorielle de l'axiome du choix
a)
Situons-nous d'abord dans le langage ensembliste. Considérons deux ensembles A et I et supposons qu'il existe une fonction surjective g prenant ses arguments en A et ses valeurs en I. Cela signifie que tous les éléments de I sont des valeurs pour les éléments de A : pour tout élément i appartenant à I, il existe un élément (au moins) appartenant à A, tel que i soit sa valeur par g.
Ceci n'interdit pas que deux éléments différents de A, x1 et x2, aient la même valeur en I par g. Considérons précisément l'ensemble Ai des éléments de A qui, par g, ont i pour valeur dans I; la figuration de tout cela donne un épi de blé dont le "germe" serait i et dont les "grains" seraient les éléments de Ai. Si i, j, k, ... sont des valeurs en I de la fonction surjective, on voit apparaître ... un champ de blé, i.e. une collection de sous-ensembles de A (Ai, Aj, Ak, ...), sous-ensembles qui sont nécessairement disjoints (par définition de ce qu'est une fonction, il n'existe dans I qu'une seule valeur correspondant à un élément de A) :
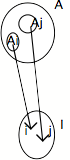
Si I est un ensemble infini, la collection des Ai, Aj, ... est elle-même infinie (on a un champ infini d'épis de blé).
Supposons une fonction de choix fc et appliquons-la à la collection infinie des sous-ensembles disjoints Ai, Aj, ...; ceci permet d'affirmer qu'il existe un ensemble dont chacun des éléments xi, xj, ... appartient à l'un des sous-ensembles disjoints Ai, Aj, ... que nous avons repéré, et dont il est l'unique représentant.
Définissons une fonction de I vers A, appellée s, qui soit telle que s(i) = fc(Ai) = xi. Il est clair que si l'on considère successivement les fonctions s puis g, on aura gs(i) = i. La fonction s est appellée section de g. S'il y a une fonction de choix, toute fonction surjective admet une section; l'écriture gs(i) = i n'est en effet possible que sous condition de l'axiome du choix, car c'est seulement à supposer l'existence d'une seule valeur dans Ai selon s que l'on peut "remonter" en A.
b) L'équivalent catégoriel de la fonction surjective est l'épimorphisme. Rappelons qu'une flèche e est un épimorphisme si, dans le diagramme suivant, h o e k o e h k
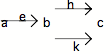
Ce qui fonde cette équivalence c'est que l'épimorphisme opère sur la totalité de b : si les actions h o e et k o e s'avèrent différentes en c, la différence ne peut provenir de "l'action" de e sur b mais seulement d'une différence entre h et k (on dit que e préserve les différences). Il en est de même pour la fonction surjective : ce sont tous les éléments de I qui sont des valeurs pour les éléments de A selon la fonction surjective.
La transcription catégorielle de l'écriture gs(i) = i sera par conséquent : e o s = Id(b) dans le triangle commutatif suivant :
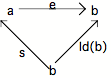
Une présentation catégorielle possible de l'axiome du choix sera ainsi : un Topos admet l'axiome du choix si tout épimorphisme admet une section. Nous noterons cette présentation : Ch 1.
Dans Ch 1 l'épimorphisme a une parenté avec l'isomorphisme. A la différence de celui-ci, il n'y a cependant d'inverseur que d'un côté : on peut dire que dans un Topos qui admet l'axiome du choix, l'épimorphisme se comporte comme un "demi-isomorphisme". Autrement dit, dans un tel Topos, l'identité catégorielle de deux objets est à demi accomplie dans l'épimorphisme. Qu'est-ce que cela signifie ? Si vous avez une action totale d'un objet a sur un objet b, le fait que l'axiome du choix opère dans le Topos où sont situés les objets a et b (i.e. le fait que cette action admette une section), implique qu'il existe entre ces deux objets pour le moins une proximité structurelle; ou encore : dans l'espace de la décision infinie, une action totale d'un objet sur un autre ne se conçoit que si ces deux objets sont "assez proches".
Une autre présentation possible de l'axiome du choix dans l'univers des Topos fait intervenir le compte-pour-un de l'objet, soit 1(a) : la flèche unique ayant a pour source et 1 pour cible (cf. 93/94 p. 19).
Nous avons déjà eu l'occasion d'utiliser le théorème selon lequel toute flèche dans un Topos admet une décomposition en un épimorphisme suivi d'un monomorphisme; autrement dit : étant donnée f, il existe m (monomorphisme) et e (épimorphisme) tels que : f = m o e (cf. 93/94 p. 21). Appliquons-le à la flèche 1(a) :
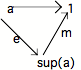
L'objet qui, dans le diagramme précédent, est la source du monomorphisme est appelé : support de a - not. : sup (a) - et l'épimorphisme qui entre dans la décomposition de 1(a) est appelé : épimorphisme support.
Une version restreinte de Ch 1, que nous noterons Ch 2, sera par conséquent : un Topos admet l'axiome du choix si tout épimorphisme support admet une section[5]. Cette version, moins forte que Ch 1, mais dans laquelle il y a une lisibilité de l'action sur 1, est en fait la présentation la plus utilisée de l'axiome du choix en théorie des Topos.
1
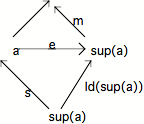
Ch 2 s'écrira par conséquent : e o s = Id (sup(a))
Différenciation logique de l'axiome du choix
4.1
Nous allons démontrer que l'unicité du vide dans un Topos équivaut à ce que sa logique soit bivalente, et qu'il valide l'axiome du choix dans sa version Ch 2.
démonstration
a) dans un Topos, si le vide est unique, la logique est bivalente - démonstration déjà faite il y a quelques années, et dont je redonne ici le squelette.
Considérons un élément f de l'Objet central C (donc une flèche f de 1 vers C). Le pullback de f et de v existe nécessairement, puisque ces deux flèches ont C comme cible. Il y a donc le carré suivant, qui est un pullback :
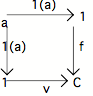
La flèche v est un monomorphisme (comme toute flèche élémentaire). Par conséquent, la flèche 1(a) est aussi un monomorphisme, en vertu du théorème (que nous ne redémontrerons pas) "le pullback d'un monomorphisme est un monomorphisme". Si 1(a) est un monomorphisme, notre pullback est un pullback de centration et notre élément f de C est en fait la centration de 1(a).
On distingue alors deux cas :
a) l'objet a est isomorphe à 0. Dans ce cas, la flèche 1(a) est similaire à la flèche 1(0). Ces deux flèches ont donc même centration (théorème fondamental de l'Objet Central). Or, par définition du faux, la centration de 1(0) est le faux (flèche F). Comme nous venons de voir que la centration de 1(a) est f, on en conclut : f = F.
b) l'objet a n'est pas isomorphe à 0. Si nous supposons que le vide est unique, tout objet a qui n'est pas isomorphe à 0 n'est pas vide, i.e. possède un élément. Considérons alors le diagramme suivant :
![]()
Supposons que h o 1(a) = k o 1(a). Il vient alors :
h o 1(a) o x = k o 1(a) o x
Mais 1(a) o x est une flèche de 1 vers 1, donc n'est autre que Id(1), puisque 1 est terminal (à l'inverse de tout autre objet, il n'y a qu'une seule flèche possible de l'objet terminal vers lui-même; métaphoriquement : l'objet terminal est cet objet singulier qui n'a qu'une seule façon de se rapporter à lui-même, et qui est l'identité : cf. 93/94 p. 14).
Ainsi : h o Id(1) = k o Id(1); d'où il suit que h = k.
Ayant montré que si h o 1(a) = k o 1(a), alors h = k, nous avons montré que 1(a) est un épimorphisme.
Finalement 1(a) est à la fois un monomorphisme et un épimorphisme. En vertu du théorème (que là aussi nous ne redémontrerons pas) "dans un Topos, une flèche qui est à la fois un monomorphisme et un épimorphisme est un isomorphisme", 1(a) est un isomorphisme. S'il existe un isomorphisme entre a et 1, il en résulte que la flèche 1(a) est similaire à la flèche 1(1), soit Id(1). Mais deux flèches similaires ont même centration. Or nous savons que la centration de Id(1) n'est autre que v, cependant que celle de 1(a) est f. Donc f = v.
Au bout du compte, notre supposé élément f de C s'avère ne pouvoir être que F (si a est isomorphe à 0), ou v (si a n'est pas isomorphe à 0). Il ne saurait y avoir de troisième action évaluante. Le Topos est bivalent (CQFD).
Nous venons de voir que si, dans un Topos, il y a unicité du vide, alors il n'y a que deux valeurs logiques. Autrement dit, si vous supposez que l'être n'est ultimement tissé que du vide, que l'être se présente à la pensée comme nom propre du vide, vous vous contraignez à reconnaître qu'en fait d'actions évaluantes, il n'y a que le vrai et le faux.
Mais vous pouvez aussi supposer qu'il y a deux (ou plus) vides différents. Ceci revient à admettre qu'il existe dans votre univers un principe différentiant intensif ou qualitatif - ontologie du virtuel, de la puissance (Aristote), ou du Chaos (Deleuze) - un principe qui ne se laisse pas élémentairement localiser : ce ne peut être par leurs éléments que ces vides se différentient, puisqu'ils n'en ont pas (cf. 94/95 p. 6) ! Par conséquent la contraposée du théorème que nous venons de démontrer dit que la multiplicité des vides, soit une ontologie de la différence intensive, suppose une multiplicité des valeurs logiques, une logique nuancée.
C'est une question de préférence ! Car en réalité toute pensée, avant même d'avoir commencé, a déjà décidé sur ce point; on est là dans les arcanes de la pré-décision onto-logique. En ce qui me concerne, je "n'aime pas" les différences intensives (je les juge obscurantistes), ma pré-décision est par conséquent d'ordre ontologique (option pour un régime extensionnel de la différence); mais je dois en payer les conséquences logiques, je dois m'arranger comme je peux de ce que, par exemple dans l'action, je n'aie le choix qu'entre deux évaluations possibles - et c'est cette élaboration qui constitue véritablement le travail philosophique. Je pense qu'à l'inverse les "intensivistes" procèdent à une pré-décision logique : ce qu'ils "aiment", c'est pouvoir se faufiler entre le vrai et le faux (Deleuze l'a explicitement déclaré dans Rhizome), mais ils doivent en payer les conséquences ontologiques : explorer jusqu'à plus soif la ramification des différences intensives.
NOTE ADDITIONNELLE SUR LA DIFFÉRENCE
La question de l'identité de la différence en tant que différence, qui est la question de l'espace de localisation auquel on assigne la différence en général (question de l'opposition entre le global et le local) est une question d'une importance actuelle absolue. Nous tentons d'y répondre en termes logiques : nous cherchons en effet à caractériser les univers possibles qui sont tels que nous puissions y spécifier la question de la différence - c'est là le sens de notre recours à la Théorie des Topos en tant qu'instance contemporaine de la logique.
En politique, cette question se formule de la façon suivante : l'action peut-elle changer la situation par modification de l'un de ses termes ? Ou encore : la politique est-elle localisable ? Si vous soutenez que toute différence locale est en définitive inscrite dans l'identité du tout, que c'est au niveau de ce tout qu'inéluctablement tout se passe, alors la seule possibilité de changement c'est le changement du tout, la rupture qualitative. L'idée léniniste selon laquelle l'Etat ne peut être traité que globalement est ce que résume la notion de Révolution prise dans son sens absolu (à savoir le remplacement massif de l'Etat bourgeois par l'Etat prolétarien). L'expérience n'a cependant pas attesté que c'était là le bon moyen de résoudre le problème de l'Etat; au lieu de le faire dépérir, comme il était prévu, on ne fait ainsi que le reproduire, qu'en perpétuer la nature. C'est que la question "Qu'est-ce qu'une localisation politique de l'Etat ?" n'a pas été résolue de façon satisfaisante; il y faut des opérateurs de pensée spécifiques qui, dans le léninisme, sont indisponibles. Ou alors vous soutenez que l'altération du tout est possible par quelque chose dont la portée est élémentaire ou locale, sans que nécessairement un autre tout n'en advienne - ce qui est produit c'est un régime du tout qui est sous une loi antérieurement non reconnaissable. Comme vous le savez, la conception de la politique que je défends assume cette deuxième option (à quoi se rattache une autre théorie léniniste, celle du "maillon le plus faible"), ce qui revient à dire que l'univers de la politique est un univers bien pointé : toute différence globale y a un test local (cf. 94/95 : p. 30 note). Nous avons vu l'année dernière que tout Topos bien pointé obéit à une logique classique : le Deux structural pur y est en position centrale (p. 31 sq). C'est le sens de la formule de Marx : La lutte des classes est le moteur de l'histoire humaine. Sous le nom de "lutte des classes", Marx fait ici du Deux de l'antagonisme l'Objet Central de la Politique, i.e. ce qui donne l'intelligibilité de l'ensemble, indépendamment du fait empirique qu'il y ait des riches et des pauvres, des gens qui sont possesseurs du capital et d'autres qui sont obligés de vendre leur force de travail - fait qui, il y insistait, avait déjà été établi auparavant par les penseurs bourgeois, et dont ne se déduit nullement que le Deux de l'antagonisme soit central pour l'espace de la Politique. Dans la "lutte des classes", la classe en elle-même n'est jamais donnée "en personne"; la politique effective consiste en un mouvement de localisation de cette différence globale. C'est tout l'office de ce qu'on pourrait appeler les opérateurs subjectifs de localisation : positions de classe, points de vue de classe; c'est à des dispositions subjectives localisables, et non à "la classe" dans sa globalité, qu'a affaire la politique effective.
La formulation équivalente de la même question dans le domaine de l'art serait : une séquence novatrice se donne-t-elle nécessairement dans une méta-conception globale de l'art, dans un projet esthétique général ? Les Romantiques se sont indiscutablement identifiés de cette façon. Mais on peut aussi estimer qu'une telle représentation de l'art par lui-même relève de l'epistemè du XIXème siècle et qu'en réalité les novations artistiques sont localement induites sans que la configuration artistique ainsi dessinée ne soit commandée par l'idée d'un programme, légitimant ainsi ce que Mallarmé appelait "l'action restreinte".
De même, dans le domaine de la science, je pense qu'il existe (et qu'il a toujours existé) des énoncés qui, tout en étant locaux (ce ne sont pas des mutations de l'axiomatique générale) ont une valeur stratégique - à l'inverse par conséquent de ce que proclame l'opinion selon laquelle "on ne trouve plus grand chose aujourd'hui".
Est-ce de cela que traite J.F. Lyotard quand il parle de la "fin des grands récits" (notre époque serait celle de la fin des grands récits politiques ou esthétiques) ? Je ne le pense pas. Le propos de Lyotard est de dire que nous sommes désormais privés du sens de l'Histoire, qu'il n'y a plus de destination du sens. Ce n'est pas dans ces termes que je situe le débat. Je pense qu'il faut plutôt se poser la question suivante : tout en ne renonçant pas à l'hypothèse selon laquelle il y aurait des différences totalisantes (comme, pour Marx, le Deux de l'antagonisme), se demander comment orienter l'opérateur de novation - dont il peut s'avérer que le point d'impact ne peut être que local. L'idée dominante aujourd'hui c'est que la différence dont la pensée est comptable est inéluctablement locale, ceci étant à la mesure de ce que, au niveau global, le Capital a tout accaparé. Autrement dit : puisque la pensée ne peut que localement, elle ne peut pas grand chose, alors que le Capital, lui, peut tout. C'est cela en définitive que signifie le thème de "la fin des idéologies". Or, il est selon moi essentiel de ne pas confondre cette conception partout répandue aujourd'hui avec le thème, que je registrais tout à l'heure à l'action restreinte de Mallarmé, selon lequel ce dont il s'agit, dans les investigations contemporaines les plus difficiles, c'est d'une tentative de novation à point d'impact local qui ne renonce pas à l'hypothèse de la différence globale (ce que Mallarmé avait en vue c'est d'ailleurs une modification radicale du Poème).
Je voudrais rappeler, à cet égard, que la psychanalyse vise dans sa pratique une différenciation globale puisque ce qu'elle a en vue c'est ni plus ni moins qu'une différenciation du sujet d'avec lui-même (qu'elle y arrive ou non selon les cas ne change rien à la nature de cette visée). C'est ce qui explique que l'on a toujours eu des difficultés à ne la considérer que comme une simple thérapeutique de tel ou tel symptôme. Mais cette différenciation globale passe par la convocation du sujet en ce point de réel où se situe l'objet de son désir; ce réel a donc pour fonction de localiser la différentiation subjective. L'enjeu d'une analyse c'est l'advenue - élémentaire (un point de réel) - de l'objet du désir autrement que sous la modalité de son être-là comme cause.
Si la question "Que peut la pensée ?" est déterminante aujourd'hui, et si elle se pose bien, ainsi que je le soutiens, dans les termes de l'opposition entre le global et le local, qui est une question topologique essentielle, il s'ensuit que les problèmes actuels de la pensée sont fondamentalement topologiques, qu'ils concernent avant tout l'espace et non le temps. Je le dirai autrement : dans la passe contemporaine de la pensée, il ne faut pas s'embarrasser du temps. C'est bien entendu une condition indispensable pour rompre avec l'historicisme; mais c'est aussi que l'exigence topologique de la pensée est obnubilée par la prévalence des catégories temporelles. C'est grâce à Lacan que l'espace n'est plus pour nous cette extériorité que se subordonne le temps conçu, lui, comme domaine privilégié de l'intériorité. Il ne faut plus perdre son temps, comme l'a fait Husserl, à scruter dans le sujet "la conscience intime du temps"; au contraire, l'espace, avec Lacan, est la bonne voie d'accès à l'intime, toujours plus féconde que le temps. Je suis indiscutablement son disciple sur ce point. Entre nous, c'est la raison pour laquelle j'ai tenté de réhabiliter la catégorie d'éternité : car qu'est-ce que l'éternité sinon une spatialisation immobile du temps ? L'éternité est donc pour moi une façon élégante de me débarrasser de la catégorie du temps. Ce n'est plus Sein und Zeit : il nous faut une théorie non temporelle du Da du Dasein. Dé-temporaliser la pensée : voilà le mot d'ordre !
b)
Reste à démontrer que si, dans un Topos, on suppose l'unicité du vide, ceci implique l'axiome du choix dans sa présentation Ch 2. Cette démonstration est facile et recourt avec un automatisme bestial aux mêmes noyaux de raisonnement que précédemment.
Considérons le diagramme de la décomposition canonique de la flèche 1(a) :
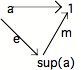
Supposons que le vide est unique. On a alors deux cas :
1. sup(a) est isomorphe à 0.
Nous savons que tout objet isomorphe à l'objet initial est lui-même initial. Il n'y a donc qu'une seule flèche de sup(a) vers 1, ce qui implique que a est lui-même isomorphe à 0. L'épimorphisme e est par conséquent l'identité de 0 et e est à lui-même sa propre section (si l'on veut : Id(0) o Id(0) = Id(0)).
2. sup(a) n'est pas isomorphe à 0.
Si nous supposons que le vide est unique et puisque sup(a) n'est pas isomorphe au vide, sup(a) a nécessairement un élément f : la flèche f telle que 1 ----f---- sup(a) existe.
Considérons alors le diagramme suivant : 1 ---f----- sup(a) ----m------ 1. En reprenant le même raisonnement que tout à l'heure, nous pouvons dire que le monomorphisme m est aussi un épimorphisme. Il est donc aussi un isomorphisme (en vertu du théorème précédemment utilisé). Qu'il existe un isomorphisme entre sup(a) et 1 revient à dire que la flèche m est similaire à l'identité de 1.
Il vient : Id(1) o e = 1(a) et par conséquent e = 1(a)
Nous avons alors le diagramme suivant :
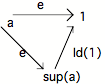
Il est aisé de voir que a ne saurait être isomorphe à 0. En effet la flèche de 0 vers 1, qui, nous venons de le voir serait alors un épimorphisme, est à l'évidence un monomorphisme, et donc elle serait aussi un isomorphisme. La supposition que a 0 implique donc que 0 1 : le Topos est dégénéré.
Par conséquent a n'est pas isomorphe à 0, et comme le vide est unique, a possède un élément. La flèche 1 -----x---- a existe.
Nous pouvons donc écrire : 1 ---x---- a ---e---- 1
Or, nous savons qu'il n'y a qu'une seule flèche de 1 vers 1 et c'est l'identité de 1.
Donc : e o x = Id(1)
Mais nous avons vu que sup(a) est isomorphe à 1; et par conséquent :
e o x = Id(sup(a))
L'axiome du choix dans sa présentation Ch 2 est valide.
Il suffit que dans un univers il y ait unicité du vide pour qu'il y ait dans cet univers une instance de choix - selon l'axiome du choix : celui-ci n'a pas besoin d'être décidé, il est contraint par l'unicité du vide dans l'univers en question.
c) Il nous faut encore démontrer la réciproque, à savoir que si nous supposons dans un Topos que la logique de celui-ci est bivalente et qu'il valide l'axiome du choix dans sa présentation Ch 2, alors dans ce Topos le vide est unique (c'est seulement alors que notre démonstration aura été accomplie car celle-ci suppose une équivalence entre deux énoncés).
démonstration
Dire que le Topos est bivalent, c'est dire qu'il
n'y a que deux éléments de l'Objet Central, le vrai et le faux. Ceux-ci étant
les centrations de deux monomorphismes de cible 1 (respectivement 1 --1, et 0 ---- 1), il résulte de la correspondance bi-univoque
existant entre élément de C et sous-objet de 1 que, dans ce Topos, il n'existe
que deux sous-objets de 1 : 1 ---- 1 et 0 ----- 1 (cf. 93/94 p. 9 et p. 19).
Considérons le diagramme de la décomposition
canonique de 1(a)
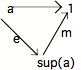
Le nombre de sous-objets possibles dans le Topos étant limité à deux, la flèche m ne peut être que l'une des deux flèches suivantes : 1 -- 1 ou 0 --- 1; autrement dit : sup(a) ne peut être isomorphe qu'à 1 ou à 0.
Si sup(a) est isomorphe à 0, l'objet quelconque a est aussi isomorphe à 0 (nous savons que dans un Topos, s'il existe une flèche de a vers 0, alors a est isomorphe à 0) et la catégorie est dégénérée. Si nous supposons que a n'est pas isomorphe à 0, sup(a) ne peut donc être isomorphe qu'à 1; et comme 1 possède 1 élément (qui est l'identité de 1), sup(a) possède aussi un élément x : 1 ---x-- sup(a) existe.
Ch 2, que nous supposons ici validé, nous permet par ailleurs de dire qu'il existe une flèche s de sup(a) vers a : sup(a) ---s-- a existe.
Nous pouvons donc écrire : 1 ---x-- sup(a) ---s--- a
L'objet a possède donc un élément (qui est s o x) et n'est donc pas vide. Nous venons donc de démontrer que, dans un Topos où il n'y a que deux valeurs de vérité et qui valide Ch 2, tout objet a non isomorphe à 0 est nécessairement non vide - autrement dit que 0 est le seul objet à l'être - CQFD.
Au total (1) : unicité du vide logique bivalente + Ch 2
Dans un Topos, il s'avère qu'une pensée ontologique, qui est ultimement une pensée de la différence (l'unicité du vide) équivaut à la figure d'un certain type de rapport entre liberté (l'espace de décision posé par Ch 2) et logique (la bivalence).
4.2
Considérons une troisième présentation de l'axiome du choix (elle sera notée Ch 3)
Alors que, par rapport à Ch 1, Ch 2 est une présentation restreinte, Ch 3 se veut une formulation aussi globale que possible de l'axiome du choix : elle doit concerner les flèches en général (et pas seulement les épimorphismes).
Une fois de plus, situons nous dans ce Topos particulier qu'est le Topos des Ensembles.
Soit deux ensembles A et B et une fonction f qui prend ses arguments en A et ses valeurs en B. Isolons dans B le sous-ensemble des éléments qui sont des valeurs effectives selon f et notons le fA. On a : y fA x x A et y = f(x)
Appelons f* la fonction qui prend ses arguments en A et ses valeurs en fA. La fonction f* est une fonction surjective extraite de f, puisque tous les éléments de fA sont des valeurs selon f. L'axiome du choix pose que, en tant que fonction surjective, f* admet une section, soit une fonction s de fA vers A.
Prenons un élément quelconque xo de A et définissons une fonction g de B vers A qui soit telle que :
(a) si y fA g(y) = s(y)
(b) si y fA g(y) = xo
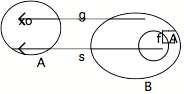
Autrement dit : si y appartient à fA, sa valeur dans A selon g sera identique à celle de la section s de f*; si y n'appartient pas à fA, cette valeur sera une valeur arbitraire xo.
Soit un élément quelconque x appartenant à A; faisons f (qui amène en fA), puis g (en l'occurence confondue avec s, qui ramène en A), puis f à nouveau (qui conduit en fA); comme, par définition de ce qu'est une section, le segment "f puis s" se ramène à l'identité, on peut écrire :
f o g o f = f
parenthèse : l'écriture f o g o f, utilisée pour des ensembles, n'est pas un abus : les Ensembles étant un Topos particulier (le Topos des Ensembles), l'écriture générale des Topos s'applique à eux sans problème.
Donnons une transcription catégorielle de ce que nous venons d'établir. Si dans un Topos, il existe, pour toute flèche f, une flèche g telle que f o g o f = f, alors ce Topos admet l'axiome du choix. C'est ce que nous noterons Ch 3. Il faut remarquer que Ch 3 ne s'applique que si l'ensemble initial A (l'objet a en langage toposique) n'est pas vide; car la chaîne précédente de raisonnements resterait valide dans cette éventualité sauf en un segment : celui où il est dit " prenons un élément quelconque xo de A" - car A, étant vide, n'a pas d'élément !
4.3
Nous allons maintenant démontrer que si un Topos valide l'axiome du choix dans sa présentation Ch 3, alors il est caractérisé par l'unicité du vide, la bivalence de sa logique et il valide l'axiome du choix dans sa présentation Ch 1.
Supposons un objet a non isomorphe à 0. La flèche f telle que a--f--1 existe nécessairement (puisque 1 est terminal). Ch 3 permet d'affirmer l'existence d'une flèche g telle que f o g o f = f
![]()
L'objet a possède donc un élément (et n'est donc pas vide).
Donc : sous condition de Ch 3, tout objet du Topos non isomorphe à 0 possède un élément 1--g --a. Autrement dit : le vide est unique (CQFD).
Mais aussi on peut écrire : 1 --g--a --f--1
Nous avons vu au cours de la première étape que, dans un tel diagramme, f s'avère être un isomorphisme et par conséquent avoir même centration que Id(1).
Si nous supposons maintenant que a est isomorphe à 0, il en résulte que f a même centration que 1(0). Et si les centrations de Id(1) et de 1(0) épuisent le nombre des éléments de C, c'est que le Topos est bivalent (CQFD).
Il faut maintenant montrer que l'épimorphisme a --e--b admet une section (i.e. que Ch 1 est valide).
- si a est isomorphe à 0 : la flèche a ----b, étant à la fois un monomorphisme (toute flèche de type 0 ----- est un monomorphisme) et un épimorphisme, est un isomorphisme. L'objet b étant isomorphe à 0, notre flèche est l'identité de 0, qui admet une section : elle-même.
- si a n'est pas isomorphe à 0 : Ch 3 permet de poser l'existence d'une flèche g telle que :
e o g o e = e
Rien n'interdit de multiplier par 1 (l'identité) et d'écrire : e o g o e = Id(b) o e; et comme on peut "simplifier" par e dans toute formule du type h o e = k o e (puisque c'est la définition même de l'épimorphisme qu'une telle formule implique h = k), on peut écrire : e o g = Id(b) : ce qui signifie que g est une section de e (CQFD).
Il faut bien comprendre que dans le Topos des Ensembles les présentations multiples de l'axiome du choix (Ch 1, Ch 2, Ch 3, ...) sont équivalentes : on peut montrer qu'elles peuvent se résoudre en un seul énoncé, qui est la formulation canonique de l'axiome. Mais si cette équivalence est identifiable à l'intérieur d'un univers décidé comme l'est celui des Ensembles, elle n'est nullement donnée dans le registre des univers possibles qui est celui des Topos en général, i.e. dans le registre logique. Le niveau logique pluralise en effet volontiers les notions qui, de l'intérieur d'un univers particulier, sembleraient identiques. Mais en outre les conditions dans lesquelles les diverses présentations de l'axiome du choix sont liées au niveau logique indiquent des caractéristiques intrinsèques de l'univers des Ensembles. Ainsi dire : Unicité du videLogique bivalente + Ch 2 (c'est notre première étape) et Ch 3Unicité du vide + Logique bivalente + Ch 1 (que nous venons de démontrer), de même que Ch 1 + Topos bien pointé Ch 3 (théorème qui est en quelque sorte l'inverse du précédent, et qui nous montre ce qui empêche, d'un point de vue logique, l'équivalence entre Ch 1 et Ch 3) c'est éclairer la singularité ontologique de l'univers des Ensembles dans lequel Ch 1, Ch 2 et Ch 3 sont effectivement équivalents.
Qu'avons-nous fait en réalité ? Nous sommes partis de l'axiome du choix dans la présentation ontologiquement unifiée qu'il a dans cet univers singulier qu'est l'univers des Ensembles. Puis nous avons procédé à une analyse de cet axiome dans la théorie des Topos, ce qui nous en a fourni une différenciation logique, traduite par les formulations variées de l'axiome (Ch 1, Ch 2, Ch 3) : l'analyse toposique révèle en effet que ces formulations ne sont pas équivalentes si l'on se situe dans le registre des univers possibles. Enfin, nous nous posons la question suivante : "quelles sont les propriétés du Topos des Ensembles qui font que la réduction à l'Un des présentations multiples de l'axiome du choix y est nécessaire ?" et cette question est celle des contraintes d'univers. Cette méthode de va-et-vient n'est pas sans rappeler celle de J.P. Sartre dans la Critique de la raison dialectique, méthode qu'il qualifie de "régressive-progressive" : notre temps d'analyse logique correspond à ce qu'est pour lui la démarche "régressive", alors que notre temps d'investigation ontologique, correspond à ce qu'il appelle la démarche "progressive". A la réserve près que Sartre se désintéresse totalement des mathématiques et que la singularité qui l'occupe dans la Critique de la raison dialectique c'est ce qu'il appelle la praxis, à savoir l'Histoire concrète, celle qui a effectivement eu lieu. Son but est, à partir de celle-ci, de penser une logique historique pure, à l'aide d'opérateurs formels d'historicité (le groupe en fusion, le groupe assermenté etc.). En d'autres termes il cherche à penser des espaces historiques possibles (les "ensembles pratiques formels") : c'est le temps "régressif" de sa démarche. Mais l'articulation des niveaux logiques ainsi dégagés doit, dans un second temps, pouvoir rendre compte de la singularité historique effective : c'est la promesse du moment "progressif". Or, il est significatif que Sartre n'a jamais écrit ce second temps qui n'est resté qu'à l'état de brouillons. Cet échec s'explique, à mon sens, par le défaut de la dimension événementielle pure qui est ce qui s'interpose entre les ensembles pratiques formels et la singularité proprement dite pensée comme contingence. Ce qui est venu à la place du deuxième tome annoncé de la Critique (qui n'a jamais vu le jour), et donc ce qui est venu à la place de l'Histoire, c'est une monographie : son Flaubert. "L'Idiot de la famille est la suite de Questions de méthode. Son sujet : que peut-on savoir d'un homme, aujourd'hui ? Il m'a paru qu'on ne pouvait répondre à cete question que par l'étude d'un cas concret : que savons-nous - par exemple - de Gustave Flaubert ?" (J.P. Sartre Préface de L'Idiot de la famille 1971, t. 1, p. 7). Je ne m'intéresse pas assez à Flaubert pour dire si la mise en oeuvre à son propos de la méthode "régressive-progressive" lui a permis de traiter son objet de manière adéquate[6].
Déjà dans Questions de méthode Sartre formule ainsi son objectif : découvrir "le point d'insertion de l'homme dans sa classe, c'est-à-dire la famille singulière comme médiation entre la classe universelle et l'individu : la famille, en effet, est constituée dans et par le mouvement général de l'Histoire et vécue d'autre part comme un absolu dans la profondeur et l'opacité de l'enfance (p. 47). Et, dans la Préface à L'Idiot de la famille, les termes seront les suivants : "Un homme n'est jamais un individu; il vaudrait mieux l'appeler un universel singulier : totalisé et, par là même, universalisé par son époque, il la retotalise en se reproduisant en elle comme singularité. Universel par l'universalité singulière de l'histoire humaine, singulier par la singularité universalisante de ses projets (...)" (Préface p. 8). La notion de projet est en effet décisive : "Déduit de quelques conduites jugées fondamentales, le projet sert ensuite d'hypothèse pour rendre compte de la totalité des conduites (...) Le résultat, unique, fait imaginer que la cause l'était aussi (de sorte que) la liberté y apparaît n'être qu'un autre visage de la nécessité; (mais cette illusion rétrospective n'est choquant fatalisme) "que si l'on n'a pas saisi que pour Sartre la liberté n'est pas le bon plaisir arbitraire, mais la manière qu'a l'homme de collaborer à la dialectique de l'histoire, de la réaliser" (P. Lejeune Le pacte autobiographique Points-Seuil 1996 p. 238-9). On peut ajouter que cette méthode Sartre a tenté de l'appliquer à son propre "cas" dans Les mots.
Revenons à notre question, qui relève d'une démarche "progressive" : à quelles conditions d'univers l'univers des Ensembles doit-il obéir pour que les diverses présentations de l'axiome du choix y soient nécessairement considérées comme équivalentes ? Les théorèmes précédents nous ouvrent à une première caractérisation de l'univers des Ensembles. On dira de façon générale qu'un univers qui est comme l'univers des Ensembles est : a) un Topos; b) qui plus est ce Topos est bien pointé, ce qui est une condition ontologique particulièrement forte, exprimée dans la théorie des Ensembles par l'axiome d'extensionnalité - il s'ensuit que le vide y est unique (un objet qui n'a pas d'élément est isomorphe à 0), et que sa logique est à la fois bivalente (démonstration ancienne, déjà sollicitée plusieurs fois) et classique (c'est notre deuxième théorème fondamental de l'année dernière - démonstration in ONTLOG p. 32); c) ce Topos possède en outre en son sein un objet nombre naturel (qui fonctionne comme l'équivalent catégoriel de ce qu'est l'axiome d'infini dans la théorie des ensembles : cf. ONTLOG p. 14); d) il admet l'axiome du choix (le théorème de Diaconescu affirme que la logique d'un Topos qui admet l'axiome du choix est classique). En réalité, on peut montrer qu'un tel univers, qui n'est pas identique à cet univers singulier, décidé, qu'est l'univers des Ensembles avec la totalité de ses axiomes, mais qui lui ressemble furieusement, est un peu moins puissant que ce dernier : certaines opérations possibles dans les Ensembles ne sont plus possibles dans cet univers. Ce que l'on obtient, à ce stade de la démarche "progressive", ce n'est pas une singularité, mais une espèce. Une espèce c'est donc ce qu'une démarche progressive permet d'atteindre comme lieu de pensabilité de la singularité. On ne revient jamais strictement à la singularité dont on était pourtant parti au temps "régressif" : la configuration obtenue est comme la singularité initiale, mais ne s'identifie pas à elle, le cercle ne se boucle pas. "Comme" est ici un opérateur de voisinage; autrement dit : le mouvement progressif ne revient pas à la singularité initiale comme telle, mais parvient à du topologique. Je pense que l'articulation de ces deux moments est une matrice décisive de la pensée[7].
5 Qu'est-ce que le classicisme en Théorie des Topos ?
Nous avons vu l'année dernière (ONTLOG p. 31 sq)
que l'analyse toposique revient à penser le classicisme comme une
structuration de l'Objet Central par le Deux considéré comme Un et Un.
Cette souveraineté du Deux structural pur s'exprime catégoriellement sous la
forme d'une isomorphie entre l'Objet Central et le co-produit de 1 et de
1, i.e. avec l'objet 1+1.
Nous avions démontré qu'un Topos bien pointé est à
la fois bivalent (il ne possède que deux valeurs de vérité, le Vrai et le Faux)
et classique : le Deux dans sa forme la plus radicale y est central. Ou encore : si dans un univers la différence est
localisable en un point, cet univers a le Deux en son centre et celui-ci n'est
pas le Deux de la différence extensionnelle mais le 1+1 du Deux structural pur.
C'est éminemment le cas de la théorie des ensembles dans laquelle l'ensemble
(0,1) - i.e. 2 - fait office d'Objet Central. La différence de ces deux Deux se
fera mieux comprendre si l'on arrive à exhiber un Topos qui soit bivalent mais
qui en même temps ne soit pas classique.
Un tel Topos est connu sous le nom de "Topos
action monoïdale 2" (et est noté : Topos M2). En raison de ses propriétés
remarquables il a donné lieu, dans la littérature mathématique, à un grand
nombre de commentaires et d'exercices qui en font un peu le panda du zoo
catégoriel.
Le Topos M2 est constitué de la façon suivante :
on part d'un ensemble X et on considère, parmi les fonctions de X dans X, les
fonctions qui sont telles que ( (x)) =
(x)[8]. est caractérisée comme une action de X dans X.
Ainsi soit (x) = x'; si on applique à nouveau sur x', on obtient toujours x'
( (x)) =
(x) = x'
Ainsi à partir d'un élément x de X, on ne peut,
par , procéder de façon successive qu'à deux actions (d'où le nom du Topos); plus exactement définit une condition de stagnation à partir du
deuxième pas.
Les objets du Topos M2 seront des couples (X,); ces objets seront donc constitués d'une part
d'un ensemble et d'autre part d'une action qui a les propriétés que nous venons
de définir pour (action monoïdale 2). Un objet du Topos M2 se
présente donc sous la forme suivante : X ----- X.
Les flèches du Topos M2 seront des flèches f qui auront pour
source des couples (X,) et pour cible des couples (Y,) où Y est un ensemble et une action monoïdale 2 de Y dans Y. Les flèches f
sont ici des fonctions de X vers Y au sens ensembliste (elles prennent leurs
arguments en X et leurs valeurs en Y). On ne retient que les flèches équivariantes,
i.e. celles qui font commuter le diagramme suivant :
Erreur !
Des objets ne peuvent pas être créés à partir des codes de champs de mise en
forme.
o f = f o
En d'autres termes : ne sont retenues comme
flèches du Topos que les flèches qui sont telles que l'élément (f(x))
est le même élément que f ((x)).
Il
est aisé de montrer que les flèches f sont associatives et que pour tout objet
il existe la flèche identique; on a donc affaire à une catégorie.
Mais cette catégorie est aussi un Topos. La démonstration complète de ce point est
particulièrement fastidieuse; dans le traité classique de Goldblatt, l'auteur
lui-même avertit avant d'en donner le texte (qui occupe plusieurs pages) que le
lecteur qui la suivra de bout en bout "aura bien gagné son salut au
ciel". Je rappelle que cette démonstration exige que l'on montre que dans
cette catégorie :
- existent les limites et les co-limites pour tout
diagramme fini (un théorème affirme que si dans une catégorie il y a un objet
terminal et les pullbacks, les limites pour tout diagramme fini existent dans
cette catégorie; de même, s'il y a un objet initial et les pushouts, y existent
les co-limites pour tout diagramme fini; "il suffit" donc de montrer
que cette catégorie possède un objet terminal, un objet initial, les pullbacks
et les pushouts)
- qu'elle admet l'exponentiation
- et qu'il y a un Objet Central
A titre d'exemple, l'objet terminal du Topos est
le couple (a, Id), où a est le singleton de a. En effet, puisque a est la
seule valeur possible dans a, il est clair qu'il n'existe qu'une seule flèche
f faisant correspondre dans a un élément quelconque x d'un ensemble X. De même,
l'objet initial du Topos est le couple (, f), où f est la fonction vide : une fonction du vide sur
lui-même et qui bien entendu n'opère rien.
On démontre que dans le Topos M2, le vide est
unique. Rappelons qu'un objet est
vide s'il n'a pas d'élément. Mais qu'est-ce qu'avoir un élément dans M2 ? C'est,
pour un objet, être la cible d'une flèche e ayant le couple (a, Id) - i.e. l'objet terminal - comme source :
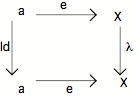
Bien entendu, ce diagramme doit être commutatif :
e(a) doit être le même que (e(a)); autrement dit : la flèche e est élémentaire à
la condition qu'elle fasse correspondre à a un point de X qui soit invariant par (l'action est dans le cas présent stagnante dès le premier
pas).
L'objet initial, i.e. le couple (, f), n'a pas d'élément et est donc vide. Par contre,
pour tout couple (X, ) tel que X (i.e. un X dans lequel existe au moins un x), on
peut toujours mettre en évidence une flèche e qui fasse commuter un diagramme
du type ci-dessus. Tout objet non initial a donc un élément. Par conséquent le
vide est unique (c'est l'objet initial).
Construisons maintenant l'Objet Central de M2. Il faut pour cela se demander ce que peut
être un monomorphisme dans ce Topos. Soit le diagramme suivant :
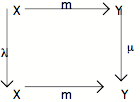
Pour que la flèche m soit un monomorphisme, il
faut qu'elle fasse correspondre à deux points différents x1 et x2 de X, deux
points différents y1 et y2 de Y (la différence des deux points initiaux est conservée par la flèche m). Si tel est le cas, ce qui se
passe c'est que m inclut dans
Y un sous-ensemble qui est en fait isomorphe à X; ce sous-ensemble est noté mX. Mais il faut encore, pour que m soit un
monomorphisme, que le diagramme précédent commute : i.e. que et opèrent de la même façon sur mX (le point dans Y selon l'action doit appartenir au sous-ensemble de Y qui est
isomorphe à X).
Dans ces conditions, un Objet Central de M2 se
présenterait de la façon suivante :
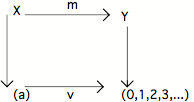
Dans le diagramme ci-dessus, il faudrait en fait
pouvoir se représenter X ----m---- Y comme la réduction à une ligne du diagramme
définissant le monomorphisme dans M2 que nous avons vu plus haut : la
figuration des actions respectivement associées aux ensembles X et Y est
"sous-entendue" pour des raisons de commodité de présentation; mais
la figure complète est en fait dans l'espace : ce serait un cube et non plus un
carré. De la même façon, le (a) du diagramme vaut pour a ---Id--- a et l'ensemble (0,1,2,3,...) qui est mis
provisoirement en place de l'Objet Central doit être considéré comme associé à
une action que nous nommerons . Et la flèche verticale de droite Y ---c--- (O,1,2,3,...), i.e. la flèche de centration, est
l'aplatissement du diagramme suivant :
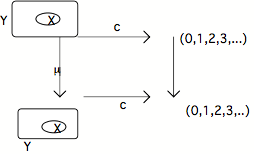
diagramme qui doit bien entendu commuter. Mais il y a ici trois
cas qu'il importe de distinguer :
a) y mX : on considère un point y qui appartient au
sous-ensemble que le monomorphisme m inclut dans Y; en vertu des propriétés du
monomorphisme, on a nécessairement (y) mX; on donne alors à c(y) la valeur 2
b) y mX, mais (y) mX (rien n'interdit cette hypothèse, puisque en
dehors de mX aucune contrainte liée aux propriétés du
monomorphisme n'opère); on pose alors que c(y) a la valeur 1
c) y mX et (y) mX; on pose alors que c(y) a la valeur 0
Etant donné un monomorphisme m, celui-ci distingue
par conséquent 3 possibilités pour les éléments de Y : pour la première, on
parlera de coïncidence entre
les actions et ; pour la troisième, on parlera d'hétérogénéité; et pour la seconde, on pourra parler d'interférence (car l'action rend possible l'action ultérieure de ). L'analyse de ces différents cas peut donc être
effectuée par un Objet Central à 3 constituants; nous désignerons donc
désormais celui-ci de la façon suivante : (0,1,2,).
Dans le diagramme qui définissait l'Objet Central,
considérons a ---v---0,1,2; il est clair que v(a) ne peut prendre qu'une seule valeur (il n'y a
qu'un seul élément dans l'ensemble a); convenons que v(a) a la valeur 2.
On voit alors que le diagramme ci-dessus, qui
développe dans l'espace Y---c---(O,1,2), commute si y mX : la valeur est en effet 2 que l'on parcourt le
carré dans un sens ou dans l'autre - il faut bien entendu pour cela que (2) = 2. Si y mX et (y) mX, le diagramme commute aussi : la valeur est alors
0 si (0) = 0. Enfin si y mX, mais (y) mX le diagramme commute (la valeur, quel que soit le
sens dans lequel on parcourt le carré, est 2) mais à la condition que (1) = 2.
est donc une action de l'ensemble 0,1,2 sur lui-même qui est telle que :
- (0) =0
- (1) = (2) = 2
est donc bien une action monoïdale 2 :
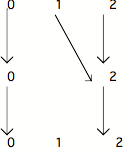
C'est ici que pointe le caractère non classique
de cette logique. On n'a pas affaire à une logique du tout ou rien puisque
ce que nous avons appelé l'interférence, et qui désigne la proximité de deux actions,
est traité de la même façon que leur coïncidence.
Combien d'éléments l'Objet Central de M2 a-t-il ?
Autant que de flèches qui font commuter le diagramme suivant :
Erreur !
Des objets ne peuvent pas être créés à partir des codes de champs de mise en
forme.
La flèche équivariante f de source a et de cible 0,1,2 telle que f(a) = 2 est la flèche Vrai (elle est
un élément de l'Objet Central);
La flèche g, qui est une autre flèche équivariante
de source a et de cible 0,1,2 telle que g(a) = 0, est la flèche Faux (et est
donc un autre élément de l'Objet Central);
Par contre il ne saurait y avoir de flèche h telle
que h(a) = 1; en effet le diagramme précédent n'est alors plus commutatif :
puisque d'un côté (h(a)) = 2 et que de l'autre côté h (Id(a)) = 1.
L'Objet Central n'a par conséquent que deux éléments, le Topos est bivalent.
Par contre il est non classique : l'Objet Central n'y est pas isomorphe à l'objet
1+1. Qu'est-ce que l'objet 1+1 dans M2 ? C'est 2 fois un objet terminal, et
l'isomorphie entre lui et l'Objet Central se donne dans le diagramme suivant :
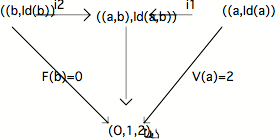
La question est de savoir si la flèche VF, dont la source est le co-produit (a,b), Id(a,b) et la cible l'Objet Central (0,1,2),, est ou non un isomorphisme; rappelons que,
sachant qu'elle est un monomorphisme (démonstration technique), il faut
déterminer si elle est aussi un épimorphisme (puisque toute flèche qui a ces 2
propriétés est un isomorphisme).
La flèche VF serait un épimorphisme si o VF = Id (0,1,2) o VF avec = Id (0,1,2). Pour que le diagramme commute, les
2 seules valeurs possibles en combinant les flèches sont 0 et 2; or nous savons
que (1) = 2; par conséquent Id (O,1,2), VF n'est pas un épimorphisme, ni donc un
isomorphisme et l'Objet Central de notre Topos n'est pas isomorphe à l'objet
1+1. Ce Topos, tout en étant bivalent, et tout en n'ayant qu'un seul vide, n'est
pas classique.
Il s'ensuit qu'il n'est pas bien pointé : cela se
déduit de ce qu'un Topos bien pointé est à la fois bivalent et classique; et
cela se confirme immédiatement : puisque Id (O,1,2), ces deux flèches parallèles
différentes (puisqu'elles ont une même source qui est l'Objet Central, qui est
par ailleurs leur cible commune) devraient, si le Topos était bien pointé, être
précédées d'une flèche élémentaire x telle que o x Id (0,1,2) o x
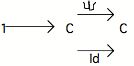
Or il n'y a pas une flèche de 1 vers C, mais deux (le Vrai et le Faux) qui conservent la différence des deux flèches et Id (0,1,2) ...
Par ailleurs on peut montrer que le Topos valide le tiers exclu; mais il n'en est pas de même pour l'équivalence de l'identité et de la double négation et la raison en est à nouveau l'existence du 3ème cas (celui que nous avons nommé le cas de l'interférence).
Considérons en effet la négation, notée ~, qui, rappelons-le, est la centration du Faux :
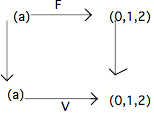
Le diagramme commute si ~ (0) = 2
Il n'est pas gênant de poser ~ (1) = ~ (2) = 0
Faisons fonctionner ~ 2 fois et nous verrons que le cas intermédiaire ne se reproduit pas par double négation, mais qu'il est renvoyé aux cas extrêmaux (comme s'il n'y avait que 2 cas, alors qu'il y en a 3 au départ).
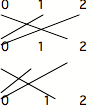
La négation dans M2 est donc
moins forte en un sens que dans un Topos qui obéit à une logique classique (car
on se meut dans M2 dans une situation où existe un cas intermédiaire) mais, en
un autre sens, elle est plus forte car elle est destructrice de quelque chose
qui est présent au départ : on part d'une situation à 3 cas et la double négation
ne réaffirme pas cette situation mais une situation qui est de type classique
(2 cas) et qui est donc plus classique que la situation initiale (le cas intermédiaire
a été incorporé à la situation Vrai)
Au moment de partir en vacances, vous avez donc deux Topos que vous pouvez emporter dans vos bagages : le Topos des Ensembles et désormais le Topos M2.
–––––––