Théorie des topos
Alain Badiou (1994-1995)
Les cinq concepts fondamentaux de l'onto-logie
la décision, le vide, la négation, la différence, et l'infini
Notes de Daniel
Fischer
La décision 1
Le vide 2
La négation 4
La différence 4
L'infini 5
Les quatre théorèmes fondamentaux de l'onto-logie 6
Théorème 1 7
démonstration....................................................................................................................... 9
Théorème 2 17
démonstration..................................................................................................................... 18
La décision
La logique, nous le savons, est une description des univers possibles de la pensabilité (la notion d'univers articulant un principe de cohérence ou de consistance et un problème d'extension qui examine à quelles conditions d'extension globale peut, ou doit, obéir une vérité locale).
La décision est ce qui, dans une pensée, fonctionne comme une prescription sur ce qui de l'être est pensable. Je soutiens qu'il est de la première importance de ressaisir dans toute pensée véritable l'élément toujours déjà là de décision quant à l'être.
J'appelle onto-logie (avec un trait d'union) le mode propre selon lequel une décision ontologique, qui concerne l'être-en-tant-qu'être de l'existant, se trouve nouée à une contrainte logique, qui concerne l'être du possible. J'ai déjà énoncé que la logique est ce qui possibilise la prescription, ce qui installe la prescription dans une pluralité de possibles; or toute prescription ontologique déploie une logique immanente qui légifère rétroactivement sur les possibles - logique immanente qui doit elle-même être ressaisie comme conditionnée (à partir de l'être tel que l'ontologie l'énonce), procès que j'ai proposé de caractériser comme une torsion (cf. 93/94: l'ordre philosophique (2)).
Cette nécessité de penser l'être du possible lui-même est présente dans toutes les grandes philosophies, mais est particulièrement frappante chez Leibniz dont l'investigation porte aussi bien sur l'être effectué ("fulguré") par Dieu que sur les lois d'être auxquelles obéit la possibilité comme telle.
Il y a pour lui deux sortes de vérités : les vérités de raisonnement et les vérités de fait. Les premières sont nécessaires et leur opposé est impossible; les secondes sont contingentes et leur opposé est possible.
Quand une vérité est nécessaire, on peut en trouver la raison "par l'analyse la résolvant en idées et en vérités plus simples jusqu'à ce qu'on en arrive aux primitives" (Monadologie § 34), dont on ne saurait donner la définition. Ces principes primitifs sont des "énonciations identiques dont l'opposé contient une contradiction expresse". Ce principe de consistance (du type A = A), qui n'est autre que le principe de non-contradiction, est ce qui se trouve ultimement garantir les vérités de raisonnement.
Quant aux vérités de fait, elles sont certes contingentes, mais l'audace leibnizienne est de tenir que leur contingence même n'est pas contingente : il faut trouver une légitimité pensable, une raison, à cette contingence. Le principe de raison suffisante - car c'est lui qui est ici à l'oeuvre - trouve en effet sa meilleure expression dans l'énoncé suivant : il y a de la contingence, mais il n'y a pas de contingence de la contingence. La raison des vérités de fait ne peut, contrairement aux vérités de raisonnement, se trouver par l'analyse car on tombe là dans un labyrinthe infini de causalités; prenons le cas de Leibniz lui-même en train d'écrire la Monadologie : "Il y a une infinité de figures et de mouvements présents et passés qui entrent dans la cause efficiente de mon écriture présente, et il y a une infinité de petites inclinations et dispositions de mon âme, présentes et passées, qui entrent dans la cause finale" (Monadologie § 36). Autrement dit : toute situation réelle est infinie (sur ce point, je me considère comme un héritier de Leibniz). Ou encore : en matière de réel, il n'y a pas de "primitif"; thèse qui est au fondement de l'anti-atomisme de Leibniz. Il ne reste qu'une seule solution : il "faut" que le principe de raison soit extérieur à la série causale elle-même infinie et in-analysable : "Il faut que la raison suffisante ou dernière soit hors de la suite ou séries de ce détail des contingences, quelque infini qu'il pourrait être" (Monadologie § 37). Ce qui est la démonstration leibnizienne de l'existence de Dieu. Pourquoi n'y a-t-il qu'un Dieu ? Tout simplement parce qu'il n'y a pas besoin de faire d'hypothèse supplémentaire : un seul Dieu suffit (au sens fort de la "raison suffisante"). Dieu se présente chez Leibniz comme un infini contingent (fonctionnant comme un principe de transcendance) dont l'unicité rend raison de la contingence. Imaginez deux Dieux : "l'un-des-deux, restant in-différent de l'autre pour toute langue pensable, ne pourrait se voir qualifier quant à sa raison d'être. Il serait surnuméraire au regard des axiomes, contingence effective, "de trop" au sens du Sartre de La Nausée" (EE p. 352).
Comment penser la contingence ? Il faut nécessairement qu'il y ait un principe d'être de la possibilité contraire aux vérités de fait. S'il n'y avait que la vérité contingente, si une vérité était absolument contingente (une vérité dont le contraire serait pur néant), cette vérité serait sans alternative, "il y aurait un abîme sans raison entre l'existence ... et les possibles inexistants, ou Idées" (ibid.) et la contingence de la vérité de fait serait alors impensable. Il y a des chevaux dans le monde : voilà une vérité de fait, comme telle contingente (il est possible de concevoir un monde où il n'y aurait pas de chevaux et que ce monde demeure un monde); mais il faut que le monde où il n'y aurait pas de chevaux soit doté d'un certain être pour que la contingence de la vérité "il y a des chevaux dans le monde" ne soit pas purement contingente. Il faut donc soutenir qu'il y a un être du pur possible - qui lui aussi obéit au principe de non-contradiction : "a le droit d'être selon le mode du possible, tout ce dont le contraire enveloppe une contradiction" (EE p. 350).
Ainsi Leibniz
part d'une distinction entre un régime discursif du raisonnement et un régime
discursif du constat, et en infère une disjonction ontologique à ses yeux
obligée : l'être se trouve scindé en l'être-en-tant-qu'être du possible et
l'être-en-tant-qu'être du réel ou de l'existant. "Dieu doit être simultanément
pensé comme cause des essences (entendre
par essence : l'être comme possible) et des existences"
(Monadologie § 43).
Ce que j'appelle l'onto-logie est la pensée synthétique de l'être qui subsume l'être du possible et l'être de l'existant (elle subsume de fait un régime de décision qui concerne l'être-en-tant-qu'être de l'existant et un régime de description qui concerne l'être-en-tant-qu'être du possible). La question du site de la pensée doit assumer l'articulation entre l'être du possible et l'être de l'existant. J'ai exposé ma conception de cette question dans L'être et l'événement (méditations 20, 21 et 22). J'y ai également exposé que si, pour moi, la pensée de l'être du possible est la logique, c'est la mathématique (et non la philosophie) qui prend en charge celle de l'existant.
Le vide
Ce qui convoque le vide à l'onto-logie et en fait une de ses catégories essentielles, c'est que le vide (ou la même chose sous un autre nom) constitue un point de suture ou de nouage obligé entre l'être et tout discours sur l'être; le vide constitue un point de capiton entre l'être et toute décision ontologique (tout logos sur l'être). La possibilité qu'il y ait un discours sur l'être suppose une position du vide.
La démonstration de ce point se trouve dans le Sophiste de Platon. Pour autoriser un discours sur l'être, il est nécessaire d'identifier ceux (les sophistes) qui pensent et parlent faux et qui, au nom du relativisme, nient la possibilité d'un discours vrai; il est donc nécessaire d'établir la possibilité du discours faux et par conséquent de réfuter l'opinion de Parménide selon laquelle le non-être n'existe pas. Il n'y a ainsi de discours tenable sur l'être que pour autant qu'on reconnait qu'il y a un être du non-être, "non-être" étant le nom platonicien du vide (cf. 21.11.92 p.3/4).
Ce thème se retrouve chez Descartes. L'opération du doute est une opération d'évidement qui suspend toute certitude (et le "doute hyperbolique" qui a recours à des hypothèses extrêmes faisant intervenir des figures extérieures à la pensée humaine, des figures de l'Autre - en l'occurence d'un "mauvais Autre" (Dieu trompeur) - va jusqu'à suspendre la certitude inhérente aux vérités mathématiques). Est ainsi constituée une pensée ne pensant rien (tout ce qu'elle est susceptible de penser serait suspendu par le doute) qui, pour Descartes, joue le rôle d'un sophiste intérieur. "Je pense, je suis" est l'assertion d'un pur point qui est un point vide, assertion certaine en existence, mais vide en contenu (autre que sa capacité à douter, à soutenir sa propre opération d'évidement). Le sujet lacanien sera en fin de compte le même que ce sujet asubstantiel qui advient pour la première fois à la pensée avec Descartes. Chez lui, comme chez Platon, c'est d'un point vide que s'autorise le discours sur l'être, c'est le vide qui est convoqué au point où le discours peut s'assurer d'un réel.
De Hegel, il faut lire l'admirable début de la première section du livre I de la Science de la Logique :
A. L'ETRE :
L'Être, l'Être pur, - sans aucune autre détermination. Dans son immédiateté
indéterminée, il est seulement égal à lui-même, n'est pas inégal à autre chose,
et ignore toute différence, tant à l'intérieur qu'à l'extérieur de lui-même.
Une détermination quelconque, ou contenu qui introduiraient en lui des
différences ou le poseraient comme différent d'autre chose, ne le
conserveraient pas dans sa pureté originaire. Il est le pur vide, la pure
indéterminité. - Il n'y a rien à intuitionner en lui, si du moins on peut
parler ici d'intuition; il ne peut guère s'agir que d'une intuition pure et
vide. Il n'y a également rien à penser en lui, ou il ne s'agit alors que d'une
pensée vide. L'être, l'immédiat indéterminé, est en fait un Néant, ni plus ni moins qu'un néant.
B. LE NEANT :
le Néant, le pur Néant; c'est une simple égalité avec soi-même, la vacuité,
l'indétermination et le manque de contenu absolus; indifférenciation avec
soi-même. - Dans la mesure où l'on peut parler ici de pensée (ou d'intuition),
il existe une différence entre penser (ou intuitionner) quelque chose ou rien. Ne rien penser, ne rien intuitionner,
cela a donc une signification; les deux sont distingués, et ainsi le néant est (existe) dans notre pensée ou notre
intuition; ou plutôt, il s'agit d'une pensée et d'une intuition vides, comme
dans le cas de l'être pur - Le Néant a ici la même détermination, ou la même
absence de détermination, que l'Être pur,
et est donc la même chose que lui.
C. LE DEVENIR : I. L'unité de l'Être et du Néant.
L'Être pur et le Néant pur sont donc la même chose. La vérité n'est ni l'Être, ni le Néant, mais le fait que l'Être est passé (et non passe) dans le Néant, et le Néant dans l'Être ... Leur vérité est donc ce mouvement de disparition immédiate l'un dans l'autre : le Devenir.
Comme chez Platon, le discours sur l'être exige d'en passer par la vacuité, sous les espèces ici de l'indétermination vide ou de l'intuitionné pur, i.e. ce par quoi l'Être pur est la même chose que le Néant. Et le il y a comme tel ce n'est donc ni l'Être ni le Néant, qui sont deux purs signifiants, mais le passage de l'un dans l'autre. "Lacanisons" quelque peu : on pourrait dire que le devenir c'est ce que l'Être représente pour le Néant, ou encore que le devenir c'est le sujet en tant qu'il est présenté dans l'intervalle entre l'Être et le Néant. Hegel ne définit-il pas son propos de la façon suivante : "présenter l'absolu non pas seulement comme substance mais comme sujet" (préface de la Phénoménologie de l'Esprit). C'est pour autant qu'avec l'Être et le Néant, on a affaire avec l'identité sous deux noms différents, que le devenir, "ce mouvement de disparition immédiate l'un dans l'autre", i.e. l'écart vide entre ces deux noms, surgit comme sujet.
Il est remarquable que dans le calcul des prédicats du premier ordre, il est toujours précisé qu'on n'utilise pas de modèle vide. Soit la formule (x) P(x) (x) P(x). Elle n'est pas valide dans un modèle vide, car si rien n'empêche d'avoir une assertion universelle quant au vide, on ne peut pas asserter "il existe x" dans un modèle qui ne comporterait aucun x (même si P(x) avait la signification de "x n'existe pas"). En d'autres termes, n'est pas convocable pour modéliser quelque fragment du calcul du premier ordre. Or ce point a depuis toujours été subverti par la philosophie en tant précisément qu'elle exige la possibilité d'un être du non-être, pour que le discours qu'elle tient soit garanti quant à son minimum de réel. Si on considère la logique comme étant essentiellement une entreprise de formalisation, alors la philosophie, en tant qu'elle exige une sémantique du vide, est nécessairement il-logique. C'est au contraire le mérite de la présentation catégorielle de la logique que d'être adéquate aux besoins contemporains d'une corrélation logico-ontologique (cf. 93/94 : L'ordre philosophique (1) p.3).
La négation
Elle est d'emblée une catégorie de l'onto-logie, étant à la fois un terme fondamental du discours philosophique et le nom d'un connecteur logique. C'est la force de la négation qui va être affectée par le type de décision ontologique et tout spécialement la force disjonctive de la négation (soit la force de la disjonction p ou ~ p) : la question est de savoir si la négation est bien le seul autre de l'affirmation. Une réponse positive à cette question définit le principe du tiers exclu (principe qu'assume Parménide, mais pas Platon : cf. 92/93 : 21.11.92) et exhibe la force maximale de la négation. L'exposition catégorielle montre que l'adoption du principe du tiers exclu est organiquement liée à certaines décisions ontologiques et que d'autres décisions, qui ressortissent à une conception affaiblie de la négation[1], sont liées à des modalisations éventuellement infinies entre p et ~ p, dans lesquelles ~ p ne représente qu'un extremum d'altérité, une limite de l'autre. La négation est donc en quelque sorte un sismographe de la décision quant à l'être en terme de force disjonctive.
Une autre modalité de la force de la négation est la capacité créatrice de la négation. Ici la question est de savoir si ~~p est la même chose que p. Une réponse positive signifie que la capacité créatrice de la négation est atténuée : la double négation ne fait pas advenir autre chose que l'initial. Dans une logique classique, cette limitation de la force créatrice de la négation va de pair avec un maximum de sa force disjonctive. Par contre les logiques non classiques, dans lesquelles il n'est pas vrai que ~~p p, impliquent à la fois une atténuation de la force disjonctive de la négation et une réelle force créatrice de celle-ci - partant elles impliquent une topologie qui n'est pas triviale comme dans les logiques classiques, mais une authentique création d'espace, une topologie des voisinages. Privilégier la force créatrice de la négation autorise la prescription d'un lieu, mais c'est au prix d'admettre une pluralisation de l'altérité.
La différence
Je voudrais insister sur le fait que le concept de différence n'est pas pour la philosophie un concept parmi d'autres. L'énoncé "Il y a de la différence" est en effet un réquisit essentiel pour qu'une pensée soit qualifiée comme philosophique. C'est vrai y compris du Poème de Parménide, qui peut pourtant être considéré comme le texte canonique d'une pensée de l'Un, mais qui commence par indiquer qu'il y a deux "voies s'offrant à la recherche" (même si, plus loin, c'est la "voie de l'être" qu'il enjoint de suivre).
Cela n'est cependant pas suffisant. L'assertion de la différence doit être complétée par une réponse à la question de l'espace de localisation auquel on assigne la différence en général : il s'agit ici de l'opposition entre le global et le local. Dans une conception extensionnelle, comme celle de l'ensemblisme, toute différence globale a un test local; les différences ne sont pas appréhendables par une intuition différentiante des totalités, mais par un trait. Si deux ensembles ne sont égaux que s'ils ont les mêmes éléments, il en résulte que deux ensembles sont différents si un élément au moins appartient à l'un et pas à l'autre. Vous concluez donc toujours, quant à une différence globale (entre deux ensembles), à partir d'une différence locale (la monstration d'un élément qui entre dans la présentation de l'un, et non dans celle de l'autre - Un seul être vous manque et tout est dépeuplé). Il y a ici opposition avec Deleuze (les différences sont chez lui de l'ordre de la flexion globale) et, au-delà, avec Bergson : c'est l'opposition d'un type de multiplicités composées d'éléments à un type de multiplicités qualitatives qui supposent une intuition globale de ce qu'elles sont. Opposition qui était déjà celle de l'atomisme épicurien (pour lequel toute différence est ultimement ponctualisable) avec le stoïcisme (pour qui une différence renvoie toujours à une totalité). cf. aussi : 93/94 : Structure dialectique du Topos bien pointé
L'infini
C'est une question éminemment onto-logique en ce que, dans une pensée, toute assertion d'existence concernant l'infini rétroagit sur le type de contrainte logique qui y est opératoire.
A. On le voit de façon exemplaire (et limite) à propos de tout ce qui tourne autour de la théologie négative, dont c'est la conviction fondamentale que la ressource logique comme telle entre en défaillance sitôt que le discours est aux abords de l'infini. Ce qu'on peut dire de l'infini y est toujours dans la forme du "dire ... que ne pas" : de Dieu ne sont dicibles que les attributs qui ne lui conviennent pas. L'infini fait ici trou dans la logique, ou est en soustraction par rapport à elle.
L'idée qu'il y a une corrélation entre toute assertion d'existence sur l'infini et la question de la force de la négation - idée qui n'a rien d'évident - peut, d'une certaine façon, être considérée comme héritière de ces conceptions de la théologie négative. Il est frappant que la querelle entre la logique classique et la logique intuitionniste porte toujours simultanément sur l'infini et la négation. Si, du côté de la décision ontologique, on accepte des assertions d'existence fortes sur l'infini, alors, du côté du connecteur logique, on accepte aussi une force disjonctive maximale de la négation (Descartes, Cantor). A l'inverse une réticence ou une impossibilité à admettre l'existence d'un infini actuel s'accompagne d'une théorie de la négation faible, et notamment du rejet du principe du tiers exclu (logique intuitionniste).
Cette corrélation est retrouvée jusque dans la logique lacanienne de la sexuation, qui pourtant au départ se présente elle-même comme diagonale à l'opposition de la logique classique et de l'intuitionnisme. Le "pas-tout", qui identifie la position femme, se veut en effet une négation d'un type nouveau, autre chose que ~(x), i.e. autre chose que ce qui, dans la logique aristotélicienne, est la simple négation d'une universelle, à savoir l'affirmation d'une particulière.
relire : "Sujet et Infini" in :
Conditions p. 287-305
Ce que nous dit Lacan c'est que, si l'espace de référence est fini - c'est l'espace de "la jouissance phallique, telle que déterminée de façon toujours finie par l'effet inéluctable de la fonction " (Conditions p. 294) - alors la négation va fonctionner de manière classique : "Ce pas-tout devient l'équivalent de ce qui, en logique aristotélicienne, s'énonce du particulier. Il y a l'exception" (S XX).
Mais si l'espace de référence est infini - "Quand je dis que la femme n'est pas-toute et que c'est pour cela que je ne peux pas dire la femme, c'est précisément parce que je mets en question une jouissance qui au regard de tout ce qui se sert dans la fonction de (x) est de l'ordre de l'infini" (ibid.) - le pas-tout peut alors fonctionner comme une négation d'un type nouveau. "Dès que vous avez affaire à un ensemble infini, vous ne sauriez poser que le pas-tout comporte l'existence de quelque chose qui se produise d'une négation, d'une contradiction. Vous pouvez à la rigueur le poser comme d'une existence indéterminée" (ibid.). Cette négation, singulière par sa corrélation avec une existence indéterminée, est en fin de compte une négation affaiblie : elle laisse quelque chose en suspens et ce quelque chose est l'identité de ce qui objecte à l'universelle - "c'est pour cela que je ne peux pas dire la femme".
Laissons de côté les problèmes complexes soulevés par la théorie lacanienne de la jouissance féminine ainsi que la question de savoir jusqu'où va la coquetterie que Lacan affiche avec la logique intuitionniste. Ce que je voudrais montrer ici est différent. Lacan a tenté de repenser une question que, somme toute, l'humanité s'est posée depuis toujours : "Quelle est la charge de négativité du féminin ?" Il entendait que sa réponse obéisse simultanément aux deux réquisits suivants :
- la négativité dont il s'agit doit être une négativité singulière, irréductible, dont il n'y a nulle part ailleurs exemple;
- elle ne doit pas relever de la logique classique, dans laquelle la négation d'une universelle implique l'affirmation d'une particulière; une telle négation situerait la position femme en exception de la fonction , sachant que, pour Lacan, c'est l'énoncé universel "pour tout x, (x)" qui enjoint la position homme. "(Car) Lacan n'entend nullement admettre qu'il puisse exister un x, donc un être-parlant, soustrait, radicalement, à la fonction . La castration est universelle en ceci qu'elle affecte l'accès à la jouissance de tout être parlant, quelle que soit sa position, homme ou femme" (Conditions p. 289).
La réponse de Lacan est que la position femme est dé-totalisante au regard de ce qu'il y a de circonscrit et de fini dans le pour-tout - qui est aussi un "pourtour" - masculin. Réponse qui, en elle-même, n'est pas nouvelle. Hegel ne disait-il pas déjà que la femme est "l'ironie de la communauté" ? Ce que je trouve particulièrement remarquable est que pour introduire la modalité de négation affaiblie dont il a besoin, Lacan a eu à en passer par une assertion sur l'infini. Je soutiens par ailleurs que cette assertion est pré-cantorienne (Conditions p. 296) en ce que pour Lacan la pensée de l'infini actuel est hétérogène à celle du fini : c'est parce qu'il n'y a pour lui "de concept de l'infini qu'en termes d'inaccessibilité opératoire" (ibid.) et qu'il pense cette inaccessibilité comme une "faille", que l'infini peut précisément être convoqué par lui pour fonder une "existence indéterminée".
On voit par conséquent, Lacan servant ici d'exemple, que toute décision ontologique sur l'infini affecte le statut de la négation et, de proche en proche, tout l'espace logique. C'est pourquoi l'infini est une catégorie onto-logique (et pas seulement ontologique).
B. Il est de même impossible de penser l'infini sans penser en même temps la différence et plus précisément la différence de la différence, i.e. celle qui oppose les différences qualitatives et les différences extensives - Hegel est celui qui a mené la pensée de cette corrélation jusqu'au bout.
relire :
méditation Hegel in EE p. 181-190
"Quelque chose" - un pur terme présenté - n'est pour Hegel déterminé qu'autant qu'il se laisse penser comme autre qu'un autre : "L'extériorité de l'être-autre est l'intériorité propre du quelque chose". "Ceci signifie que la loi du compte-pour-un est que le terme compté possède en lui-même la marque-autre de son être" (EE p. 182). "Or la chose est. Son être s'accomplit par le franchissement du non-être, c'est-à-dire l'outrepassement de la borne" (EE p. 183). Ce que Hegel transforme en devoir : "L'être-de-l'un consiste en ceci qu'il faut outrepasser la borne (...) (Mais) dès lors que l'outrepassement est une loi intérieure du point d'être, l'infini qui en résulte n'a pas d'autre être que celui de ce point (...) l'infini n'est que le vide où opère la répétition du fini. Chaque pas-de-plus convoque le vide où il peut se répéter" (EE p. 184) "et ainsi de suite à l'infini". Le procès de cette "répétition ennuyeuse et toujours identique" est celui du mauvais infini.
"(Mais) outre qu'il se répète, le quelque chose détient, qui excède cette répétition, la capacité essentielle, et présentifiable, à se répéter" (EE p. 185). "Considéré comme présence du procès répétitif, le "quelque chose" a rompu son rapport extérieur à l'autre, d'où il détenait sa détermination. Il est maintenant rapport-à-soi, pure immanence, puisque l'autre est devenu effectif dans le mode du vide infini où le quelque chose se répète" (EE p. 186). Hegel nomme cette virtualité, qui est récollection qualitative du mouvement même de la répétition, le bon infini.
"Ce qui constitue le bon infini est la présence du mauvais" (EE p. 185), ou encore c'est "le répétitionnel de la répétition, en tant qu'autre du vide" (EE p. 186), ce qu'il y a de qualitatif dans toute insistance quantitative.
Les quatre théorèmes fondamentaux de l'onto-logie
J'en donne l'énoncé, pour l'instant, en
"langue naturelle" :
Théorème 1
(il fait noeud de l'infini comme récurrence ou progression - le mauvais infini
de Hegel - et de l'infini actuel réellement décidé - que l'on peut assimiler au
bon infini) : tout Topos qui admet un opérateur de succession en position
universelle admet un objet intrinsèquement infini. Ou, comme aurait pu dire
Hegel : s'il y a du mauvais infini, il y a du bon.
Théorème 2 (il fait noeud du vide, de la différence et de la négation) : si dans un Topos il y a unicité du vide et que la logique du Topos est classique (i.e. que la négation y est forte), alors le Topos est bien pointé (i.e. toute différence y a un statut local).
Théorème 3 (il fait noeud de la décision et de la négation) : tout Topos qui admet l'axiome du choix est classique.
Théorème 4 (il fait noeud de la différence et de la négation) : la topologie de la double négation (i.e. la topologie des voisinages) permet d'extraire de tout Topos un sous-Topos classique.
Nous allons, cette année, démontrer les deux premiers de ces quatre théorèmes fondamentaux de l'onto-logie, démonstrations où va se déployer la capacité d'éclaircie de la théorie des Topos quant à l'onto-logie.
Théorème 1
Théorème 1 : Tout Topos qui admet un opérateur de succession en position universelle admet un objet intrinsèquement infini.
A. Il y a trois approches possibles quant à la question de l'infini[2] :
a) On peut partir de la succession, de ce qui s'enracine dans l'idée de progression "à l'infini" : c'est ce que fait Hegel avec son concept du "mauvais infini".
b) On peut adopter une démarche purement axiomatique ou opératoire : fixer des opérations telles que l'espace d'exercice de ces opérations soit nécessairement infini, mais sans qu'il soit besoin de thématiser explicitement cet infini. C'est la démarche choisie par Peano dans sa présentation axiomatique des nombres entiers (Le Nombre et les nombres : chap. Peano).
c) Enfin il peut y avoir une définition intrinsèque de l'infini.
1. En ce qui concerne la première démarche, la question est la suivante : qu'est-ce qu'une itération quand rien ne la borne ? Comme je l'ai indiqué dans EE, à propos des méthodes par lesquelles l'infini advient au pensable sans la médiation de l'un, ce qui intervient ici c'est une dialectique du "déjà" et du "encore" (EE p. 165). Il y faut en effet : a. un "déjà", un point d'être, donc un multiple présenté, ou existant; b. une procédure - une règle - telle qu'elle indique comment je "passe" d'un terme présenté à un autre (autre qui est aussi bien le même); c. une novation à chaque pas, dialectiquement liée à l'invariance de la règle utilisée : car c'est une même opération qui incessamment produit de l'autre (le terme engendré par la répétition est incessamment différent de ceux qui le précèdent). Demandez-vous s'il existe quelque chose du même ordre dans le geste violent du démiurge du Timée au moment où il façonne l'âme du monde, "harmonisant de force avec le Même la nature de l'Autre qui répugne au mélange" (35b); l'idée profonde que Platon exprime ici est que pour qu'il y ait univers, la nature fuyante de l'altérité doit être contrainte par force à l'harmonie.
2. Quant à la seconde approche, on y retrouve, comme nous le reverrons, un point de départ et un opérateur de succession mais aussi quelque chose de plus. La logique de succession procède à une récollection totalisante qu'inscrit le saut à l'universel : c'est de tout x que l'on peut dire qu'il a la propriété P. Mais il s'agit d'une totalisation indéterminée : quand on écrit "tout x", on n'a que l'inscription du tout, non sa détermination.
3. Or c'est une détermination intrinsèque de l'infini que vise la troisième approche. Celle-ci peut procéder par la voie positive ou bien par la voie négative.
a) voie positive, c'est celle de Dedekind : on dira qu'un ensemble (Dedekind parle de "système") est infini s'il existe une correspondance biunivoque entre lui et une de ses parties propres; dans le cas opposé, il s'agit d'un ensemble fini. Cette définition de l'infini systématise une remarque déjà faite par Galilée : il y a une correspondance biunivoque entre les nombres entiers et les nombres qui sont des carrés. Il suffit de poser f(n) = n2. Il semble donc qu'il existe des correspondances biunivoques entre l'ensemble tout entier et une de ses parties propres. Cette partie a dès lors "autant" d'éléments que l'ensemble lui-même. De ce que l'énoncé "le tout est plus grand que la partie" (énoncé qui est un axiome des Eléments d'Euclide) soit apparemment faux dès lors qu'on considère les totalités infinies, Galilée concluait qu'il était absurde de vouloir penser des ensembles infinis actuels. C'est ce paradoxe que Dedekind transforme audacieusement en définition des ensembles infinis (sur tout ceci voir : Le Nombre et les nombres chap. Dedekind).
b) voie négative (car, à l'inverse de la précédente, elle procède par une négation d'existence) : il n'y a pas de correspondance biunivoque entre un ensemble infini et un ordinal fini.
On peut remarquer que ces deux définitions de l'infini proposent des définitions également très différentes du fini. Pour la première, un ensemble fini est un ensemble dans lequel il n'existe pas de correspondance biunivoque entre lui et une de ses parties (la littérature mathématique appelle "Dedekind-fini" un tel ensemble); il s'agit d'une définition négative du fini. Dedekind est ici proche de Descartes, pour qui l'idée de l'infini est plus claire que celle de fini. Pour la deuxième définition, un ensemble fini est un ensemble dans lequel il y a une correspondance biunivoque entre lui et un nombre entier; le fini -c'est le fini naturel - est nombré par un ordinal fini. La question est alors la suivante : un ensemble Dedekind-fini peut-il coïncider avec un ensemble fini naturel ? Il est saisissant qu'on ne puisse démontrer une telle coïncidence qu'en utilisant l'axiome de choix, i.e. une décision sur l'infini - ce qui, par parenthèse, montre bien qu'une telle identité n'a rien de trivial : le fini, Descartes a bien raison, n'a aucune originarité claire et est bien plus obscur que l'infini.
B. L'exposition catégorielle, de ce qu'elle est susceptible d'exhiber la logique sous-jacente à toute décision sur l'infini, va permettre de penser la corrélation interne de ces trois approches, ou saisies, de l'infini - ce que la pratique séparée de chacune ne permet pas d'établir. Plus précisément l'exposition catégorielle permet de montrer que si un univers contient l'infini[3], les trois approches doivent être assumées conjointement - en d'autres termes, qu'il n'existe logiquement qu'un seul concept de l'infini (entendre "logiquement" au sens de ce qui s'inscrit dans un univers possible).
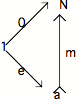
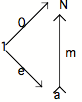
1. On peut déjà remarquer que a -----f---- b est impossible à itérer : "l'action" f se spécifiant d'être en quelque sorte la marque sur b de a, toute "action" partant de b ne saurait être que différente de f.
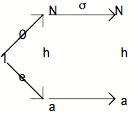
Il s'ensuit que, dans l'univers catégoriel si caractéristique par la pauvreté de ses matériaux (des objets et des flèches), ne peut être itérée que la flèche a ----f---- a. Le point de départ "élémentaire" sera bien entendu un élément de a, soit la flèche 1 -----e----- a. De sorte qu'une succession possible pourra se présenter de la façon suivante :
![]()
et s'écrire de la façon suivante : f o f o f o ....o e.
Il faut remarquer qu'avec le "diagramme de la succession" 1 ----e--- a ----f--- a, on dispose d'un point de départ élémentaire et d'une capacité d'itération, mais pas de la "novation à chaque pas" dont j'ai parlé auparavant. Rien n'interdit en effet que f puisse être Id(a), auquel cas on aurait affaire, non pas à une répétition indéfinie (le "mauvais infini" que nous cherchons à caractériser), mais à une répétition stagnante qui incessamment ramène à l'initial.
2. Il s'agit donc de capturer le concept de répétition, i.e. ce qui serait en position universelle par rapport au diagramme précédent. Conformément à la définition de la limite, il doit s'agir d'une configuration diagrammatique du même type que le diagramme de succession, et par rapport auquel elle doit être en position de subsomption et d'unicité. Ce que nous cherchons à déterminer est en fait un schème de la succession : pas seulement la chose, mais une instance du concept dont la chose relève, présentée de façon immanente dans l'univers lui-même, selon le génie propre à la théorie des catégories - cf. "Pensée de la logique ...".
On dira qu'une telle capture a lieu s'il existe une flèche h unique de N vers a qui fait commuter le diagramme ; soit :
(1) h o O = e
(2) h o = f o h
1 ----0---- N ---- ---- N est en position de subsumer 1 ---e---- a ----f----- a (en raison de la commutation dans le triangle et dans le carré). L'unicité de la flèche h est ce qui permet de remplir la condition d'unicité incluse dans la définition de la limite.
Si dans un Topos, on a une configuration du type 1 ----0---- N ---- ---- N, qui est telle que, pour tout autre diagramme répétitif du type 1 ---e---- a ----f----- a, il y a effet de capture (i.e. s'il existe h telle qu'il y a commutation de l'ensemble du diagramme), alors on dira que la première configuration est en position universelle. N est appelé : objet nombre naturel (ONN).
3. Le point suivant est celui de la productivité de . Est-ce qu'avec la limite du diagramme de succession nous disposons d'une "novation à chaque pas" qui, nous l'avons vu, fait défaut au diagramme élémentaire ? Peut-on dire qu'avec 1 ----0---- N ---- ---- N, il y a incessamment du nouveau (i.e. du "mauvais infini") ?
Soit o o ... n fois; notons le : n.
3.1 Nous allons démontrer le théorème suivant : pour qu'avec n il y ait répétition indéfinie (et non pas stagnante), il faut que n q pour q n.
démonstration
a) assumons le lemme suivant (que je ne démontre pas) : s'il existe un ONN, alors existe une flèche dite prédécesseur (notée ) de N vers N telle que :
(1) o O = O. Autrement dit, il y a commutation du triangle suivant :

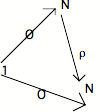
(2) o = Id(N). Autrement dit, il y a commutation du triangle suivant :
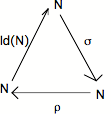
On voit pourquoi la flèche est appellée "prédécesseur" : (2) exprime le fait que, composée avec l'opération de succession , elle annule celle-ci puisqu'elle ramène à l'initial et (1) exprime le fait que O n'a pas de prédécesseur.
b) lemme 2 (démonstration triviale) : si existe, il en résulte que est un monomorphisme.
Rappelons qu'un monomorphisme est une flèche conservant les différences qui la précèdent. Si g et h sont deux flèches différentes, f est un monomorphisme si f o h f o g; on peut aussi l'exprimer par sa contraposée : h = g f o h = f o g.
Soit deux flèches f et g, supposons que o f = o g; pour que soit un monomorphisme, il faut donc que f = g.
o f = o g o o f = o o g
Or o = Id(N)
Donc Id(N) o f = Id(N) o g
et f = g
c) lemme 3 : il se déduit de façon évidente que si est un monomorphisme, alors n est aussi un monomorphisme.
En effet, si une flèche f est un monomorphisme, i.e. si h = g f o h = f o g, f peut être "simplifiée" dans toute équation du type f o h = f o g; donc si f est répétée n fois, f peut être "simplifiée" autant de fois que nécessaire pour obtenir en fin de compte g = h.
d) lemme 4 (démonstration facile - simple manipulation littérale) :
Supposons que n = q pour q n (i.e. l'hypothèse opposée à celle que nous voulons établir). Exprimée en "langue naturelle", cette équation dit que la répétition de n fois ramène à un point déjà parcouru (le trajet constitue par conséquent un cercle), point qui est séparé du départ de l'itération par la répétition de q fois :

n = q n o O = q o O
On peut "saucissonner" n en écrivant que n = q o n-q
Donc q o n-q o O = q o O
Or q est un monomorphisme (lemme 3); par conséquent n-q o O = O (q est simplifiable dans l'équation précédente).
"Re-saucissonnons" n-q en écrivant : n-q = n-q-1 o et introduisons la flèche prédécesseur de la façon suivante :
n-q-1 o n-q-1 o o O = n-q-1 o O
Or n-q-1 o n-q-1 = Id(N); et n-q-1 o O = O (car si o O = O, c'est également vrai n-q-1 fois)
ce qui permet d'écrire : Id(N) o o O = O
i.e. o O = O
Ainsi quand on suppose que n = q pour q n, alors o O = O. En "langue naturelle" : si la répétition de n fois fait une boucle à un endroit de son trajet, c'est que ça bouclait dès le départ (il y avait une répétition stagnante dès la première application de l'opérateur). Ou encore : quand la répétition ne produit pas incessamment du nouveau, c'est qu'elle n'en a jamais produit.
Nous avons donc bien démontré que, pour qu'avec n il y ait répétition indéfinie et non stagnante, il faut que n q pour q n. Ou : o O O n q pour q n.
3.2 Mais est-ce bien le cas que n q pour q n ?
Considérons le diagramme de succession particulier qu'est : 1 ---F--- C ------ C (F est la flèche faux et est la négation). S'il existe un ONN, le schème de la répétition dans lequel il est inclus doit subsumer ce diagramme élémentaire.
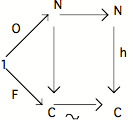
Supposons que o O = O (i.e. qu'il y ait "répétition stagnante") :
La commutation du diagramme implique que h o O = F.
Donc : o h o O = o F = V (la flèche vrai)
Or o h = h o ; donc : h o o O = o F = V
Nous avons supposé que o O = O; par conséquent h o O = V
Or la commutation du diagramme exige que h o O = F. Donc F = V (ce qui n'est possible que dans une catégorie dégénérée). Je rappelle en effet que nous avons démontré que le faux est distinct du vrai dans une catégorie non dégénérée (cf. "Pensée de la logique ...").
Le résultat auquel nous sommes parvenu peut donc s'exprimer de la façon suivante : si on considère un Topos non dégénéré (i.e. un Topos où il n'y a ne fût-ce qu'une seule différence), alors le vrai est distinct du faux, ce qui implique par conséquent que o O O et donc (implication établie en 3.1) que n q pour q n.
Dans un
univers possible qui comporte une multiplicité effective (un univers où existe
de la différence en général, i.e. un Topos non dégénéré), il y a nécessairement
de l'indéfini, du "mauvais infini" - ou encore : il y a du nombre -
et ce pour autant qu'il y existe un concept de la succession.
Il est essentiel de comprendre qu'avec ce concept de l'infini nous disposons d'un opérateur de succession (pour une succession qui n'est pas bornée) mais non d'une existence de l'infini. C'est très précisément ce que Pascal reproche au Dieu de Descartes, à savoir de n'être au fond qu'un opérateur logique, au lieu d'être avant tout une existence. Nous avons vu, par ailleurs, que pour que les formules de Lacan concernant la sexuation puissent fonctionner, celui-ci répugne à admettre que l'infini soit autre chose qu'un opérateur, et donc à accepter l'idée d'un infini actuel. En toute rigueur, on ne peut même pas parler encore d'un "concept de l'infini"; ce que nous venons de démontrer, c'est seulement que, étant donné un élément de N de la forme n o O (qui est une flèche de 1 vers N, et donc un élément de N), on peut toujours produire un autre élément de N en refaisant . Autrement dit : tous les n o O sont différents.
4. Est-il possible de passer catégoriellement à quelque chose qui soit une récollection qualitative du mouvement de la répétition, quelque chose qui soit donc comme une infinité intrinsèque ?
Ceci va nous amener à nous poser la question du caractère infini de l'objet N (objet nombre naturel). Mais comment parler de la dimension de N (et à plus forte raison de son infinité) alors qu'en théorie des catégories N, comme tout objet, n'a qu'une existence littérale (N "n'a pas d'intérieur") ? Nous partirons d'une remarque de Pascal selon laquelle quelque chose est infini si l'adjonction de quelque chose d'autre ne l'affecte en rien (remarque que l'on peut considérer comme une anticipation de la définition de l'infini qu'a donnée Dedekind); ainsi de Dieu, on peut dire qu'Il n'est pas affecté dans Son infinité immanente par l'adjonction de fini que représente la création du monde (celle-ci ne rétroagit en rien sur Lui).
Supposons que nous ayons un Topos avec un objet nombre naturel N; l'objet N+1 existe dans ce Topos (puisque le concept de Topos implique à la fois l'existence de l'objet terminal et celle de la somme ou co-produit de deux objets). Par analogie avec la remarque de Pascal, nous allons nous demander si, N étant supposé un objet infini, N+1 peut-il être dit "le même" que N; autrement dit N et N+1 sont-ils isomorphes ? Si oui, nous aurons alors démontré que N, le support de la répétition, est tel que l'adjonction de 1 le laisse identique; ou encore : le lieu où insiste la différence (le "encore un") est lui-même soustrait à l'insistance.
démonstration (belle démonstration qui met en jeu les ressources proprement géométriques de la démarche catégorielle[4]).
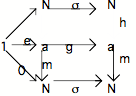
a) Considérons le diagramme qui exprime que N+1 est le co-produit, ou la somme, de N et de 1; considérons l'objet quelconque qui, de même que la limite N+1 du diagramme, est lui aussi cible d'une flèche de source N et d'une flèche de source 1 (et qui est en même temps cible de la flèche unique dite "flèche co-produit"), et supposons que cet objet est N lui-même. Nous obtenons le diagramme suivant que nous appelerons diagramme A :
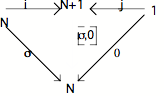
Re-marquons la flèche i sous le sommet du triangle; on obtient le diagramme A'
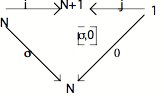
i
N+1
Ce nouveau diagramme permet de visualiser la flèche i o ,0, que nous appelerons : la flèche t; cette flèche est une flèche de N+1 vers N+1 et peut donc, combinée à une flèche de 1 vers N+1, être considérée comme une flèche itérative, capturable par 1 ---0--- N ------ N dans le "diagramme de la succession".
Reportons sur celui-ci les relations qui unissent 1, N et N+1 et nous obtenons un diagramme que nous appelerons diagramme B
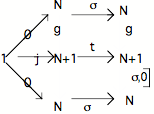
Dans tout Topos qui contient un objet nombre naturel N, la flèche unique g de N vers N+1 existe nécessairement, en raison des propriétés de N.
Si on se reporte au diagramme A, on voit que ,0 o j = 0. Par conséquent le triangle inférieur du diagramme B commute.
Par ailleurs, le diagramme A' nous permet d'écrire : ,0 o t = ,0 o i o ,0
et comme ,0 o i = (diagramme A), on peut écrire : ,0 o t = o ,0. Par conséquent le carré inférieur du diagramme B commute aussi.
Comme l'ensemble du diagramme formé par le triangle et le carré supérieurs commute en vertu des propriétés définitoires de N, on peut en conclure que l'ensemble du diagramme B commute.
Or le diagramme B a la forme d'un "diagramme de la succession"; s'il commute, c'est qu'il en est effectivement un, ce qui implique que la flèche "de droite" qui va de N vers N (,0 o g) est unique. Nous ne connaissons qu'une seule flèche unique de N vers N, et c'est l'identité de N. Ce qui nous permet d'écrire :
,0 o g = Id(N) (équation 1)
b) Considérons la flèche combinée 1 ---0-- N ---i-- N+1, soit i o 0, qui est une flèche de 1 vers N+1; sa combinaison à t donne une flèche itérative 1 ---i o 0--N+1 ---t-- N+1.
Ce qu'exprime le diagramme suivant, que nous appelerons diagramme C :
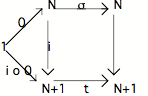
Mais la flèche g o du diagramme B est, comme la flèche i, une flèche de N vers N+1. Si on construit un diagramme de la forme du diagramme C, mais dans lequel la flèche qui va de N vers N+1 est la flèche g o , on obtient un diagramme que nous appelerons le diagramme D.
Il est possible de montrer - par une série de manipulations littérales simples (que vous pouvez faire à titre d'exercice) - que tant le triangle que le carré du diagramme C sont commutatifs; idem pour le diagramme D. Et donc le diagramme C et le diagramme D, dans leur ensemble, sont commutatifs. Mais s'ils le sont, la flèche qui va de N vers N+1 est unique (propriété définitoire de N). Par conséquent :
i = g o équation (2)
c) Re-portons la flèche g du diagramme B, qui va de N vers N+1, sur le diagramme A; nous obtenons le diagramme E :
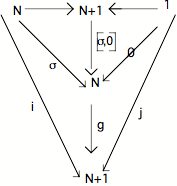
Nous savons que le diagramme B commute, et par conséquent tous les diagrammes qui le constituent commutent aussi, dont son triangle supérieur gauche; ce qui permet d'écrire :
g o O = j
Par ailleurs nous savons que g o = i (équation 2).
Les deux triangles inférieurs du diagramme E sont par conséquent des diagrammes commutatifs. L'ensemble du diagramme E est donc lui aussi commutatif. Il en résulte que la flèche g o ,0 est nécessairement une flèche unique et doit donc, étant une flèche de N+1 vers N+1, être identique à l'identité de N+1 :
g o ,0 = Id(N+1)
Mais comme ,0 o g = Id(N) (équation 1),
on obtient, en combinant les deux équations précédentes, le résultat suivant :
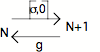
N et N+1 sont isomorphes
CQFD.
N est intrinsèquement infini.
5. Récapitulons les acquits : N - objet nombre naturel - est le support possible d'une itération indéfinie (§ 3.) et est intrinsèquement infini (§ 4.). Ceci correspond respectivement à ce que nous avons caractérisé comme la première démarche concernant l'infini (le "mauvais infini" hégélien) et la troisième (la démarche intrinsèque, placée sous le patronage de Dedekind). Reste à considérer si N est également le support possible d'un point de vue opératoire sur l'infini, ainsi qu'y invite l'axiomatisation de Peano.
Sa présentation est la suivante :
(1) ( x) (x) = 0
Il n'y a pas d'entité telle que 0 soit son successeur; 0 ne succède pas, c'est réellement un point de départ. C'est ce qu'on pourrait appeler l'axiome du point de départ. Il écarte, entre autres, la possibilité d'une boucle qui reviendrait sur 0.
(2) (x) = (y) x = y
Deux entités qui ont le même successeur sont identiques. La succession ne saurait être que linéaire.
(3) (a) si 0 possède la propriété P, (b) et s'il est vrai que, à chaque fois qu'une entité x possède la propriété P, alors le successeur de x la possède aussi, (c) alors tout x possède la propriété P.
C'est la propriété d'induction complète (dont on peut remarquer la parenté avec le thème du péché originel : si Adam (0) a péché, et que le péché est "héréditairement" transmissible, alors tous les hommes sont pécheurs). Il faut bien voir qu'à ne considérer que les segments (a) et (b) de l'induction complète, on ne peut tirer que des résultats successifs un à un; rien n'autorise à fonder un tout (tout x) - rien, sauf que c'est précisément la règle que, axiomatiquement, l'on se fixe. Poincaré voyait dans cette postulation universelle, véritable saut dans la pensée, l'essence, en même temps que la limite, de la pensée mathématique; à savoir : la capacité à tirer une conclusion universelle de prémisses opératoires. Le "tout x" du segment (c) est précisément la supposition d'un Tout que rien ne permet d'intuitionner, car il n'est pas contenu dans les prémisses opératoires des segments précédents (et qui sont les seules qu'admet sans réserves le demi-intuitionniste qu'est Poincaré).
Les
axiomes de Peano prennent-ils sens par rapport à N, l'objet nombre naturel de
la théorie des catégories ?
L'axiome (1) a une traduction immédiate : o O O (i.e. l'impossibilité que nous avions postulée pour l'itération de faire boucle). De même pour l'axiome (2), en raison du fait que est un monomorphisme (lemme 2 du § 3.). Mais il n'en est pas de même pour l'axiome (3).
Donnons-en la version ensembliste. Soit le champ où opère l'opérateur de succession , et A un sous-ensemble de (A ). La propriété d'induction complète se transcrit de la façon suivante :
(a) si 0 A
(b) et si x A (x) A
(c) alors A =
1. Nous avons déjà un concept catégoriel de l'inclusion () : c'est celui de sous-objet. En effet, un sous-objet est une classe de monomorphismes tous similaires entre eux; les monomorphismes étant des conservateurs de différences, celles-ci se marquent "à l'intérieur" de l'objet cible (c'est une façon de parler, puisqu'un objet, en théorie des catégories, n'est qu'une lettre et n'a pas d'intérieur; la seule façon d'y marquer des différences, c'est précisément de l'inscrire dans le réseau de flèches que définit le sous-objet). Le concept ensembliste d'inclusion a affaire à la même chose : au regard d'un sous-ensemble A qui est inclus dans B, toute la question pour une entité x se résume à "y être ou ne pas y être"; la fonction du sous-ensemble est donc bien, là aussi, de marquer une séparation ou une différence vis-à-vis de l'ensemble dans lequel il est inclus. On posera par conséquent que la transcription catégorielle du sous-ensemble A inclus dans est un monomorphisme m de cible N.
2. Considérons la supposition (a) 0 A.
La
transcription catégorielle de 0 est la flèche 1 ---0-- N; A, étant transcriptible
sous la forme d'un monomorphisme m de cible N, est également une flèche. Il
faut donc se demander quelle est la possible inscription catégorielle de l'appartenance
d'une flèche élémentaire à une autre flèche dont la cible est la même que celle
de la première.
Soit le diagramme suivant :
On dira que la flèche 0 appartient à m s'il existe une flèche élémentaire e dont la cible est l'objet source de m et telle que le diagramme ainsi constitué commute. Soit : m o e = 0. On conçoit d'ailleurs que la transcription du concept d'appartenance d'un élément à un ensemble requiert obligatoirement le concept catégoriel d'élément.
3. Considérons la supposition (b) x A (x) A.
L'idée sous-jacente est la suivante : si on applique à un élément de A, ce qui en résulte reste dans A; ou encore : toutes les entités produites par l'application de sont présentées par A. On reconnaît là le schéma de l'inclusion.
Sa transcription catégorielle sera par conséquent : o m m. Or, nous savons que deux sous-objets d'un objet quelconque du Topos (deux monomorphismes de même cible) peuvent être comparés (on peut dire que l'un est "inférieur" à l'autre : cf. 93/94).
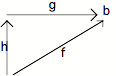
On dit que f g, ou que f est "inférieure à g", s'il existe une flèche h telle que g o h = f.
Ce qui donne dans le cas présent :
La transcription de la supposition (b) revient à supposer qu'il existe une flèche g de a vers a, et que le diagramme ainsi constitué commute. Soit : m o g = o m.
4. Enfin, la transcription de la conclusion (c) A = est que le monomorphisme m de cible N dont nous supposons l'existence est équivalent à Id(N). Soit : m Id(N). Ou encore : m et Id(N) sont deux monomorphismes similaires - cf. "les concepts de l'immanence" p.3 - ils sont le "même" sous-objet.
Récapitulons : si nous arrivons à démontrer que le monomorphisme m dont nous supposons l'existence dans le § 1. et qui est tel qu'il obéit aux conditions des § 2. et 3., est équivalent à Id(N), alors nous aurons démontré que le système (N,,0) valide les axiomes de Peano.
Nous aurons d'ailleurs de ce fait désaxiomatisé les axiomes de Peano (puisqu'ils auront été transformés en propriétés démontrables de N). Mais aussi, nous serons passé d'une totalisation (c'est de tout élément de A qu'on peut dire qu'il est un élément de ) à une identification (le monomorphisme m s'avère équivalent à l'identité de N). Jusqu'à présent j'ai insisté sur le mouvement de désobjectivation qui était impliqué par l'installation dans la logique (la réduction de l'objet à une existence littérale : la lettre est, pour reprendre l'expression de Beckett dans Cap au pire, "l'imminimisable moindre" de l'objet). Le passage d'une totalisation à une identification est un mouvement essentiel de l'installation logique qui complète le précédent. Et en effet dans A = les multiplicités élémentaires sont considérées au regard du Tout que postule "pour tout x appartenant à A"; alors que le mouvement qui aboutit à m Id(N) est un mouvement de détotalisation qui établit en fin de compte une relation d'identité (celle qui "lie" N à lui-même).
A l'inverse toute décision ontologique opte pour ceci que l'objet ne se réduit pas à la lettre; et cette option d'un point d'irréductibilité littérale est elle-même suivie d'un mouvement de totalisation ressaisissable dans quelque "totalité concrète" (Althusser). Ce qu'il est essentiel de ne pas méconnaître, c'est le marquage réciproque des deux mouvements : le fait que l'installation dans la logique s'effectue sous l'horizon d'une décision ontologique, et, à l'inverse, qu'il y a dans toute décision ontologique la trace repérable de contraintes logiques. Celles-ci sont, nous l'avons vu, généralement méconnues. Mais le mouvement d'installation logique lui aussi répudie la décision ontologique qui lui sert d'horizon; et ce qui en porte malgré tout la trace, c'est, à mon avis, le caractère fuyant de l'identité qu'il produit : comme si cette identité portait avec elle l'ombre de la totalité répudiée, comme si elle était intérieurement marquée par une pluralité évanouie.
Ces questions ont une grande importance dans le domaine politique. Nul n'ignore qu'une des formulations du débat politique actuel est de savoir si le réel d'une identité est ultimement une totalité (son expression massive est représentée par les diverses conceptions communautaristes) ou non (c'est la voie universaliste d'une certaine tradition républicaine française). Ma conviction, vous le savez, est que la voie dé-totalisante, celle de la logicisation, est en fin de compte la voie authentiquement progressiste. Il n'empêche que, y compris dans le cadre de cette option-là, nous sommes, à un moment donné, sommés de dire quelle est notre décision ontologique sous-jacente[5]. Car il y en a toujours une : il est illusoire (et politiquement erroné) de croire que la voie universaliste a absenté toute trace de la totalité. Ce qu'elle traite, ce n'est pas une absence de totalité, mais des débris de totalité. Il n'y a pas d'installation logique pure; aussi loin que l'on pousse dans une voie, l'autre voie est fatalement reconvoquée comme son ombre portée. De sorte qu'il y a en réalité, dans la tâche de la singularisation, deux choix : le choix de la voie empruntée, puis le choix de tenir compte, au sein de celle-ci, des traces ou des débris irréductibles de l'autre. Exercice : appliquer ce qui vient d'être dit à la question du voile islamique à l'école.
Revenons à notre théorème.
démonstration
Figurons à nouveau la transcription catégorielle de la supposition (a) :
et celle de la supposition (b) :
Considérons le diagramme 1 ---e-- a ---g-- a; nous reconnaissons le schéma de l'itération, comme telle capturable par 1 ---0--- N ------ N dans le "diagramme de la succession".
Il existe par conséquent, dans le diagramme ci-dessous qui redistribue sous une forme quelque peu différente les flèches que nous connaissons, une flèche unique h qui fait commuter la partie supérieure de ce diagramme :
Mais la transcription de la supposition (a) nous assure que le triangle inférieur commute également; et il en est de même pour le carré inférieur, qui est la transcription de la supposition (b). Par conséquent l'ensemble du diagramme commute.
Il en résulte que la flèche m o h est nécessairement une flèche unique et doit donc, étant une flèche de N vers N, être identique à l'identité de N (nous avons déjà utilisé à plusieurs reprises ce raisonnement; monotonie de la démonstration catégorielle ...).
Si m o h = Id(N), c'est que Id(N) m
Or m Id(N)
Par conséquent : m Id(N)
Nous venons de démontrer que
si m o e = O (a)
et si m o g = o m (b)
alors m Id(N) (c)
Ni plus ni moins que l'induction complète. Par conséquent le système (N,,0) valide les axiomes de Peano.
6. Ce n'est pas pour autant, une fois acquis, ainsi que nous venons de l'établir, qu'il n'y a qu'un seul concept catégoriel de l'infini, qu'on peut estimer en avoir fini avec l'infini (ce serait un comble !). Car la question que nous lègue la théorie des ensembles est celle de l'existence d'une pluralité d'infinis : la dissémination de l'infini auquel elle procède rompt l'accord intrinsèque entre l'infini et l'Un qui formait le socle de toute la tradition antérieure (notamment théologique); rupture suffisamment inquiétante pour que Cantor lui-même ait cru devoir consulter les cardinaux de Rome sur les conséquences de sa découverte. Or y a-t-il sens, en théorie des catégories, à parler de plusieurs infinis ? Nous nous arrêterons, provisoirement, au seuil de cette question, car nous ne disposons pas, au stade où nous en sommes, des moyens mathématiques pour pouvoir y répondre.
Théorème 2
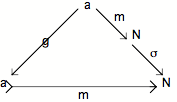
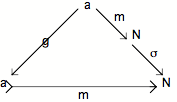
Théorème 2 : si dans un Topos il y a unicité du vide et que la logique du Topos est classique , alors le Topos est bien pointé.
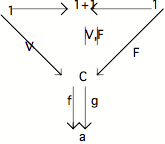
Assumer la possibilité de la différence revient, dans un Topos, à supposer l'existence de deux flèches différentes de même source et de même cible (i.e. de deux flèches parallèles différentes) en effet la différence de deux flèches qui, soit ont une source différente, soit ont une cible différente, est immédiatement perceptible. Affirmer "Il y a de la différence", c'est supposer que f et g sont différentes dans le diagramme suivant :
![]()
Mais rien ne nous dit ce qu'est cette différence intrinsèque supposée; dans l'univers catégoriel, qui, nous l'avons dit à maintes reprises, est un espace de l'extériorité (i.e. dans lequel les seules déterminations sont externes), il faut introduire des différentiants nécessairement externes qui nous permettront de penser rétroactivement la différence supposée. Celle-ci doit par conséquent être encadrée par autre chose qu'elle-même, elle doit être contextualisée, et la meilleure façon pour cela est de faire préceder f et g par une flèche h. Une telle flèche h qui, agissant avant deux flèches parallèles f et g, est telle que si f o h g o h, alors f g est appelée, rappelons-le, un épimorphisme.
Mais la différence f o h g o h elle-même n'est pas non plus attestable; ce n'est qu'une condition contextuelle relative. De contextualisation en contextualisation on est en fin de compte ramené au global, i.e. à la catégorie elle-même dans laquelle la différence est située. Or, dans un Topos, pour peu qu'il ne soit pas dégénéré, il y a au moins une différence dont nous sommes sûrs, c'est celle qu'il y a entre 0 et 1 (cf. "Catégories à clôture cartésienne") : 0 et 1 garantissent qu'il y a de la différence en général pour peu qu'eux-mêmes soient différents (i.e. non isomorphes).
L'attestation minimale, ou élémentaire, de la différence sera par conséquent donnée par le diagramme suivant :
![]()
f o x g o x f g
Les flèches f et g différent en un point
(métaphoriquement : par le point "piqué" en a par 1 ---x--). On dira que f et g sont élémentairement différentes.
La flèche élémentaire x sert de validation locale
pour la différence entre les flèches f et g.
On dira qu'un Topos est bien pointé si, dans ce Topos, deux flèches parallèles différentes sont toujours élémentairement différentes (toute différence s'y avère en un point).
Un Topos bien pointé, de par la logique extensionnelle de la différence qu'il implique, est un univers possible qui "ressemble" à l'univers de l'ontologie ensembliste. Ce qui est admirable est que cette logique de la différence prescrit aussitôt sa conséquence ontologique : si un Topos est bien pointé, tout objet vide y est isomorphe à l'objet initial 0. On démontre ici la connexion générale entre la thèse sur la différence et deux thèses sur le vide: son unicité et sa position fondatrice (initiale).
démonstration
Soit un Topos bien pointé, qui ne soit pas un Topos dégénéré. Considérons un objet a non initial (i.e. qui n'est pas isomorphe à zéro); un tel objet existe nécessairement puisque le Topos n'est pas dégénéré.
De même existent nécessairement la flèche O a (qui exprime le caractère initial de 0) et la flèche Id(a). Ces deux flèches sont des monomorphismes de même cible a; et comme il n'y a pas d'isomorphisme entre leurs sources (puisque a est supposé non isomorphe à 0), ces sous-objets sont réellement "deux" : ils ne sont pas similaires. Ils ont par conséquent des centrations effectivement différentes (qui, elles aussi, existent nécessairement dans un Topos) et qui sont des flèches parallèles (puisqu'elles vont de a vers C).
Nous voici donc en situation d'avoir deux flèches parallèles assurément différentes. Comme notre Topos est bien pointé, la différence globale de ces deux flèches s'avère obligatoirement par l'existence d'un élément x de leur source commune; ceci impose que a possède au moins un élément, et par conséquent a n'est pas vide. Nous avons ainsi démontré que si a n'est pas isomorphe à zéro, alors il n'est pas vide. Ce qui se dira aussi bien : s'il est isomorphe à zéro, alors il est vide.
Dans un Topos
bien pointé, "vide" et "zéro" (ou initial) s'avèrent être
des concepts de même extension donc substituables l'un à l'autre. Et comme nous
savons qu'il n'y a qu'un zéro (au sens catégoriel : tous "les" zéros,
ou toutes les lettres qui les nomment, sont isomorphes), il faut en conclure
qu'il n'y a qu'un seul vide. Ainsi l'unicité fondatrice (initiale) du vide
est-elle l'effet ontologique de la thèse en pensée sur la différence[6].
Celle-ci prescrit également une conséquence logique : un Topos bien pointé obéit nécessairement à une logique bivalente (nous avons déjà démontré ce théorème). Autrement dit : penser la différence selon un critère local engage à une logique qui n'admet comme valeurs de vérité que le vrai et le faux.
Alors que dans une logique bivalente les valeurs de vérité prennent place dans un espace dont la structure est algébrique, celle-ci est topologique dans une logique non-bivalente : un énoncé y sera associé à un "espace de valeurs" (celles-ci pouvant être en nombre infini) délimité par Vrai et Faux et dans lequel il sera en voisinage plus ou moins grand par rapport à ces valeurs limites; on dira par exemple de tel énoncé qu'il est "presque vrai" s'il est associé à une valeur située près de Vrai et de tel autre qu'il est "indécidable" si la valeur qui lui correspond est dans une tension intermédiaire entre Vrai et Faux. Il ne s'agit pas ici d'une logique de la décision, mais d'une logique de l'approximation.
Cependant l'équivalence que pose le théorème que nous voulons démontrer est l'équivalence entre le concept de Topos bien pointé et le concept de classicisme. Il faut donc nous donner un concept catégoriel de ce qu'est une logique classique, ce qui nous permettra de saisir la différence - voire la possible disjonction - entre classicisme et bivalence. En effet, l'analyse toposique de ce qu'est une logique classique montre que celle-ci ne se réduit pas à la bivalence, i.e. à l'existence de deux valeurs de vérité (le Vrai et le Faux). Il en résulte que la logique de certains Topos peut être classique même si le nombre de valeurs de vérité y est supérieur à deux (j'en donnerai un exemple plus loin) et qu'inversement elle peut être non classique alors même qu'il n'y en a que deux.
Ce qui caractérise une logique classique c'est qu'elle
établit la souveraineté du Deux; c'est ce qui, ultimement, en fait une
logique de la décision : ce qui évite en effet de s'égarer dans un labyrinthe
d'options (comme dans une logique de l'approximation) est quelque chose de plus
fondamental que le choix sans recours entre deux valeurs de vérité parce
qu'il n'y en a que deux (ce serait une
interprétation vraiment statique de la décision); il s'agit de la souveraineté
du Deux alors même qu'il y a plus de deux valeurs de vérité. L'analyse toposique revient à la penser comme une
juridiction de l'Objet Central sur le Deux considéré comme Un et Un. En
d'autres termes la souveraineté du Deux s'exprimera catégoriellement sous la
forme d'une isomorphie entre l'Objet Central et le co-produit de 1
et de 1, i.e. avec l'objet 1+1.
Qu'est-ce à dire ? Ce que l'objet 1+1 permet d'envisager c'est le Deux dans sa dimension structurale pure, sans référence à une discernabilité préalable : c'est un objet qui fait du Deux avec deux fois le même objet, le Un marqué deux fois. Ce qui est en jeu ici c'est la difficile question du rapport du Deux structural et d'une différence que l'on dira extensionnelle (p. ex. la différence supposée entre deux objets ou deux flèches préexistantes)[7]. Si ces deux Deux ne sont pas distingués, alors il ne saurait y avoir de logique du Deux, mais seulement une ontologie du Deux. S'il n'y a en effet qu'une seule espèce du Deux, subsumant les autres (ainsi chez Hegel, l'écart nul posé entre Être et Néant), la décision ontologique est rabattue sur la logique qui ne peut être discernée d'elle - il est significatif que le traité d'ontologie de Hegel s'intitule : La Logique; il est également certain que l'in-différence entre réel et possible est chez Hegel ce qui fonde sa célèbre maxime : "Tout ce qui est réel est rationnel et tout ce qui est rationnel est réel".
Considérons le diagramme suivant :
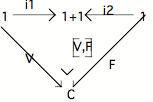
Comme tout Topos implique l'existence de l'objet terminal et l'existence d'une co-limite pour tout diagramme fini, la somme, qui est la co-limite du diagramme constitué par deux objets non liés (ici : 1 et le même objet 1 re-marqué) et les injections correspondantes i1 et i2 existent nécessairement; il en est de même pour C ainsi que pour ses éléments V et F (dont l'existence est impliquée par la définition du Topos, pour peu que celui-ci ne soit pas dégénéré); la flèche unique allant de 1+1 vers l'objet C et qui fait commuter l'ensemble du diagramme existe aussi nécessairement, par définition du co-produit (C partage avec l'objet 1+1 la propriété d'être cible de deux flèches ayant 1 pour origine) : elle est notée V,F suivant les conventions adoptées pour le co-produit.
On dira que la logique d'un Topos est classique si la flèche V,F y est un isomorphisme.
Le théorème que nous voulons démontrer se formule par conséquent ainsi : si un Topos est bien pointé cela implique que, dans ce Topos, la flèche V,F du diagramme précédent est un isomorphisme. La stratégie de la démonstration est la suivante : a) établir que la flèche V,F est un monomorphisme; b) établir qu'elle est aussi un épimorphisme. Le théorème sera alors démontré car nous savons que dans un Topos toute flèche qui est à la fois un monomorphisme et un épimorphisme est un isomorphisme (c'est le lemme 5 de la démonstration que je vous ai faite il y a quelques années).
a) la flèche V,F est un monomorphisme.
V,F o f = V,F o g f = g
La démonstration de ce point est difficile et technique et je ne vous la donne pas; je pense d'ailleurs que sa difficulté a partie liée avec la complexité pour la pensée de la question de la différence des sexes (cf. note 8). Si vous admettez que la flèche V,F est un monomorphisme, cela nous autorise à dire que ce que j'ai appelé le Deux structural pur est un conservateur de différences quant à sa signification logique, i.e. sa corrélation avec l'Objet Central (métaphoriquement : il y a un certain pouvoir filtrant du Deux structural).
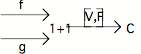
b) la flèche V,F est un épimorphisme
démonstration
On peut écrire, en raison de la commutation du triangle de gauche : V = V,F o i1
et, par conséquent, f o V = f o V,F o i1 ainsi que g o V = g o V,F o i1
Soit l'hypothèse f o V,F = g o V,F
Il s'ensuit que : f o V = g o V,F o i1 = g o V
En procédant de la même façon sur le triangle de droite, on obtient : f o F = g o F
Notre point de départ est que le Topos est bien pointé; ceci implique que si f et g sont deux flèches différentes, alors il existe une flèche élémentaire e dont la cible est leur source commune et qui est telle que f o e g o e. Mais nous savons - c'est le théorème bien connu que nous avons démontré - qu'un Topos bien pointé est bivalent : il ne possède que deux valeurs de vérité qui sont les flèches élémentaires V et F.
Mais nous venons de voir qu'aucun des deux éléments de C - qu'il s'agisse de V (f o V = g o V) ou bien de F (f o F = g o F) - ne discrimine f et g; c'est donc que f et g ne sont pas deux flèches différentes.
Ainsi, si l'on fait l'hypothèse que f o V,F = g o V,F, on obtient le résultat suivant : f = g.
C'est donc que V,F est un épimorphisme. CQFD
Et, ainsi que nous l'avons dit précédemment, de ce résultat combiné avec la démonstration que V,F est un monomorphisme, on peut conclure que V,F est un isomorphisme. L'objet 1+1 est catégoriellement le même objet que l'Objet central. Autre façon de dire que la logique d'un Topos bien pointé est classique (et pas seulement bivalente).
Dans un univers de la décision, le Deux dans sa forme la
plus radicale est central; ou encore :
si dans un univers la différence est localisable en un point, cet univers a le
Deux en son centre et celui-ci n'est pas le Deux de la différence extensionnelle
mais le 1+1 du Deux structural pur. C'est éminemment le cas de la théorie des
ensembles dans laquelle l'ensemble (0,1) - i.e. 2 - fait office d'Objet Central.
La différence de ces deux Deux se fera mieux comprendre si l'on arrive à
exhiber un Topos qui soit bivalent mais qui en même temps ne soit pas
classique.
––––––