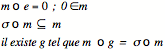Théorie des topos

Alain Badiou (1994-1995)

I 1

Récapitulation : 3

Sur la catégorie du vide 4

Parenthèse purement logique 5

Sur la catégorie de négation 5

II 6

Reprise 6

• la décision........................................................................................................................... 6

• le vide................................................................................................................................. 7

• la négation.......................................................................................................................... 7

• la différence........................................................................................................................ 7

• l’infini................................................................................................................................ 7

III 12

IV 19

Remarques sur la démonstration catégorielle 22

V 24

Démonstration 26

VI 28

Quelques rappels. 28

• Conséquence logique 31

VII 32

Sur la différence 32

I

Ce séminaire est conclusif sur la théorie des topos.

Le développement va s’articuler autour de cinq concepts fondamentaux :

- la décision,

- la négation,

- la différence,

- le vide,

- l’infini.

Quelques indications méthodiques :

Ces cinq concepts vont être déployés autour de quatre théorèmes. Nous aurons là un nouage conditionné entre une série de concepts majeurs, et l’articulation logico-mathématique afférente à ces concepts.

Nous allons donc à la fois conclure sur la philosophie de la logique, et en même temps donner un exemple significatif de la méthode par laquelle l’investigation de quelques théorèmes clefs fonctionne dans son articulation à la philosophie.

Légitimation de la liste des concepts proposés :

A mes yeux, ces cinq concepts sont les concepts organiques du mode propre sur lequel une décision ontologique se trouve nouée à une contrainte logique : onto-logie. L’onto-logie est le mode propre sur lequel une décision pensante sur l’être constitue rétroactivement, en-deçà d’elle-même, un réseau de contraintes logiques, elles-mêmes identifiables.

Cette articulation est quelque chose comme le rapport de la nécessité et de la liberté, de la pensée comme décision — affectée à l’être-en-tant-qu’être — et de la pensée comme construction — affectée à la contrainte discursive.

On peut dire que la question de la décision fonctionne comme une prescription sur ce qui de l’être est pensable, tandis que la logique va fonctionner comme une description des univers possibles de la pensabilité, comme une description des possibilités du pensable.

De ce point de vue là, la logique c’est deux choses :

- un principe de consistance : à quelles conditions peut-on dire qu’un univers est pensable comme univers ?

- un principe d’extension : que peut-on assumer du point de la pensabilité comme extension du champ du pensable, qui est fibrée intimement par la dialectique du global et du local ? A quelles conditions d’extension globale doit obéir une vérité locale ? Quelle est l’extension de la question du vrai comme possibilité ?

C’est autour de cela que va se jouer la première catégorie proposée : la décision.

Cette question, j’aimerais l’éclairer à partir de Leibniz, sur un point particulier qui est la nécessité de penser l’être du possible lui-même. Non pas de fonctionner dans une opposition de l’être et du possible, mais de traiter le possible à sa racine. Il faut bien que le possible, en tant qu’il est pensé, soit. Il faut donc qu’il y ait un être minimal du possible qui se distingue de l’être comme effectivité. Chez Leibniz, on va aussi trouver une nécessité d’investigation logique du possible selon son être — à quelle loi obéit la possibilité comme telle ? — et un principe d’investigation de l’être effectué ou fulguré par Dieu.[1]

Art 33 de la Monadologie. Point de départ significatif : «Il y a deux sortes de vérités, la vérité de raisonnement, la vérité de fait». Leibniz va déclarer que les premières sont nécessaires et que leur opposé est impossible.

Ce que Leibniz va dire c’est : quand la vérité est nécessaire, on en peut trouver la raison par l’analyse. Elle va se laisser décomposer en idées plus simples jusqu’à ce qu’on en vienne aux idées primitives. L’exemple que prend Leibniz, c’est l’exemple des mathématiques.[2] Au bout de cette chaîne, on trouve un principe de consistance, purement et simplement : on ne peut pas soutenir le contradictoire de quelque chose si ce contradictoire nous exhibe une contradiction expresse.

On passe à la deuxième filière : «La raison suffisante se doit trouver aussi dans les vérités contingentes ou de fait». Elles ne sont donc pas telles que leur contingence soit elle-même contingente. Même lorsqu’on a affaire à une existence contingente, on doit trouver une raison de ce fait. Il doit y avoir une légitimité pensable de cette contingence elle-même. Il y a de la contingence, mais il n’y a pas de contingence de la contingence (principe de raison suffisante).

Le point fondamental est que cette raison de la contingence ne peut pas se trouver par l’analyse parce que l’analyse va à l’infini. La thèse leibnizienne est que toute situation est infinie, infinie au sens du continu («labyrinthique» ). Le sujet lui-même, en tant que sujet monadique est une perspective infinie sur l’univers infini. En matière de réel, il n’y a rien de primitif. Ce qui explique que Leibniz polémiquera contre toute conception atomistique de la nature, qui est décomposable (Lucrèce).

Comment peut-on rendre raison de la contingence en tant que non contingente ? Il faut que le principe de raison soit extérieur à la série causale. Le passage clef est le suivant (c’est la démonstration leibnizienne de l’existence de Dieu) : «Comme tout ce détail n’enveloppe que d’autres contingents antérieurs ou plus détaillés, dont chacun a encore besoin d’une analyse semblable pour en rendre raison, on n’en est pas plus avancé : et il faut que la raison suffisante soit hors de la suite ou séries de ce détail des contingences, quel qu’infini qu’il pourrait être.

Et c’est ainsi que la dernière raison des choses doit être dans une substance nécessaire, dans laquelle le détail des changements ne soit qu’éminemment, comme dans la source : et c’est ce que nous appelons Dieu». Il n’y a qu’un Dieu parce qu’il n’y a pas besoin de faire une hypothèse supplémentaire. Il n’y aurait pas de raison suffisante à ce qu’il y ait deux dieux. Le second serait d’une contingence dont la contingence serait elle-même contingente, ou il en faudrait un autre transcendant aux deux. Le principe est ici un principe transcendant, extérieur à la série contingente.

Comment peut-on récapituler cette scission de la vérité ?

Au cœur des choses, il faut mettre l’opération de possibilité, au sens suivant :

• Les vérités nécessaires sont celles dont la contradictoire est impossible. La question de la possibilité est donc sous-jacente à la question de la nécessité, en particulier la contradictoire expresse est un point d’impossible pour la pensée. Contre ce point de butée, il y a les énonciations identiques.

• Du côté des vérités de fait : si elles nous sont pensables — la question de Leibniz est celle du pensable — quoique contingentes, c’est parce que leur contingence même n’est pas contingente. Pour qu’une vérité de fait contingente ne soit pas contradictoire dans sa contingence, il faut qu’il y ait un être de la possibilité contradictoire. C’est cela qui va être la chicane la plus décisive. Si le contraire n’a aucun être, alors il n’y a que la vérité contingente, bloquée sur elle-même, sans alternative. Une chose sans alternative, ou bien elle est nécessaire — ce qui n’est pas le cas —, ou elle est absolument contingente.

Par conséquent, si on veut penser la contingence, il faut qu’elle soit homogène à une raison : il n’y a pas d’autre ressource que de penser qu’elle n’est pas elle-même contingente. La possibilité contraire est vraiment. Elle a un principe d’être quelconque. L’univers où il n’y aurait pas de chevaux, il faut qu’il ait un être. Pour soutenir l’intelligibilité de la vérité contingente, il faut donc soutenir qu’il y a un certain être du pur possible. Par conséquent, le régime d’être de l’être va, à son tour, se scinder. Il va y avoir l’être-en-tant-qu’être du possible, et l’être-en-tant-qu’être du réel, ou de l’existant.

On peut dire, dans un autre registre que celui de Leibniz, qu’on va avoir une scission entre l’être-en-tant-qu’être, et l’être-en-tant-qu’existence. La pensabilité de l’être va subsumer cette distinction entre l’être-en-tant-qu’être et l’être-en-tant-qu’être-de-ce-qui-est effectivement-existant.

Récapitulation :

On part d’une distinction discursive, entre le régime discursif du raisonnement, et le régime discursif du constat, c’est-à-dire entre un régime axiomatique et un régime descriptif. A partir de cette scission discursive, s’infère une disjonction ontologique obligée, entre l’être-en-tant-qu’être du possible même, et l’être-en-tant-qu’être de l’existant comme tel.

Dans le vocabulaire de Leibniz, cela veut dire : Dieu doit être pensé simultanément comme cause des essences (l’être comme possible), et des existences.[3] Il faut bien penser l’être de façon à ce qu’il donne de l’être à la possibilité.

Nous conviendrons de dire que la question de la pensée — du site de la pensée, de la région de la pensée — doit assumer une articulation entre l’être du possible et l’être de l’existant, et nous appellerons logique l’investigation de l’être du possible, et mathématique l’investigation de l’être de l’existant.

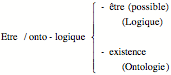
Finalement, l’onto-logique va, en effet, subsumer un régime de décision qui concerne l’être-en-tant-qu’être de l’existant, et un régime de description qui va concerner l’être-en-tant-qu’être du possible. Les opérateurs de l’onto-logique vont devoir assumer cette subsumption et cette tension.[4]

Sur la catégorie du vide

Le point qui convoque le vide à l’onto-logie, c’est que le vide — ou la même chose sous un autre nom — constitue un point de suture obligé entre l’être et tout discours sur l’être. La possibilité qu’il y ait discours sur l’être suppose qu’il y ait une position du vide (ou éventuellement du rien, du néant...). C’est pourquoi c’est une catégorie fondamentale de l’onto-logie.

La première démonstration de ce point se trouve dans le Sophiste de Platon. On voit très bien dans le Sophiste que l’obligation du néant — d’un être du non-être — est entièrement liée à la possibilité du discours, en particulier à la possibilité du discours faux. Pour autoriser un discours sur l’être, il est nécessaire d’identifier ceux qui soutiennent qu’il n’y a pas de tels discours. Pour cette identification primordiale, il faut assumer un être du non-être. Par conséquent, il n’y a discours sur l’être, tenable — tel que ça puisse être un dire —, il n’y a la possibilité d’un dire sur l’être qu’autant qu’on reconnaît qu’il y a un être du non-être. La nécessité de réfuter Parménide résulte non pas de la démonstration de la fausseté de la théorie de Parménide, mais du constat que la théorie de Parménide ne peut pas se dire.

Qu’est-ce que ça veut dire que Parménide l’ait constitué comme un dire ? Il est essentiel de constater que ce dire parménidien demeure un dire poétique, pas seulement parce que c’est en vers, mais parce que ça demeure inspiré  : comparution devant la déesse et non pas un dieu. La théorie parménidienne ne constitue pas la possibilité d’un dire dialectique, par opposition à un dire poétique. Raison pour laquelle Platon dira dans le livre X de la République que le bannissement des poètes est la chose la plus surprenante. La répudiation des poètes est un parricide, comme celui du Sophiste, à moins que ce ne soit un matricide : le meurtre de la langue.[5]

Autres exemples :

• C’est une convocation absolument présente chez Descartes, au point pur du Cogito. Le doute est une opération d’évidement. Le doute hyperbolique est un évidement, y compris de ce dont on ne peut pas s’évider. C’est la constitution d’une pensée qui ne pense rien, car quoi que ce soit qu’elle pense est suspendu par le doute. Donc, lorsqu’il va y avoir le «je pense, je suis» , il va y avoir l’assertion d’un point vide, certain en existence, mais vide en contenu. Sujet a-substantiel, réduit au point pur de son opération, vide. Or, c’est cela qui fait qu’il y a chez Descartes un discours sur l’être : le «je pense» comme vacuité pure, sauf qu’il existe. On va avoir le vide existant d’une opération d’évidement, qui est ce qui va suturer le discours cartésien à l’être. Le cogito est la réitération de cette opération essentielle qui est de garantir le discours sur l’être en un point de suture au vide.

Nous trouvons encore le vide convoqué au point où le discours peut s’assurer d’un réel. Le discours ne peut s’assurer d’un réel qu’en convoquant un vide.

Et, chez Descartes, comme dans le Sophiste, cela ne peut s’assurer que sous l’hypothèse maximale du discours faux qui vérifierait qu’il n’existe pour le discours aucun point de suture.

• Hegel. L’exemple hégélien est encore d’une toute autre nature. Dans son point de départ, la dialectique serait inengageable s’il n’y avait la réversibilité essentielle entre l’être et le néant. Cf. l’envoi extraordinaire de la Logique. La procédure hégélienne[6] va exiger comme opérateur central : la vacuité. L’intuitionner vide est ce par quoi l’être pur est, aussi et en même temps, le néant pur, de sorte que le il y a originel n’est ni l’un ni l’autre, mais le passage de l’un dans l’autre. Le devenir va être aussi et en même temps sujet, parce que le devenir est ce que l’être représente pour le néant. Mais être et néant sont deux purs signifiants. Si on cherche à ce qu’il y ait autre chose que le mot, ce qu’on trouve c’est le vide. «Mon but est de présenter l’absolu non pas seulement comme substance, mais aussi comme sujet» (Préface de la Phénoménologie ). Ceci est en jeu dès le début. Pour cela, il faut que la suture à l’être soit dans le devenir. La réversibilité entre les deux signifiants être et néant n’est possible que par la convocation du vide.

Nous sommes fondés à dire que le vide, la vacuité, la possibilité d’un être du non-être, sont constamment exigés pour que le discours soit garanti quant à son minimum de réel. Cela se donne dans la catégorie de l’Autre (Platon), le point vide du cogito (Descartes), la vacuité de l’être et du néant (Hegel).

Parenthèse purement logique

Il est un point très intéressant à constater. Si on prend les logiques formalisées classiques, il est toujours sous-entendu qu’on n’utilise pas des modèles vides :

Il y a une sorte de subordination implicative du quantificateur au quantificateur $ : . Cette formule est manifestement non valide dans un modèle vide. L’ensemble vide n’est pas convocable pour modéliser tout énoncé fragmentable dans la logique du premier ordre. C’est ce point qu’en un certain sens, la philosophie a toujours déjà subverti. C’est en ce sens que les formalisations de la logique du premier ordre sont a-philosophiques. En philosophie, il y a toujours une sémantique du vide.

Donc, on peut soutenir que, si on entend par logique, la formalisation traditionnelle des langages logiques, alors on peut dire soit que la logique est a-philosophique, parce qu’elle exclut la sémantique du vide, soit que la philosophie est illogique, parce qu’elle exige une sémantique du vide.

C’est pourquoi, si on veut reconstruire une corrélation logico-philosophique, alors il faut modifier la signification du mot logique, cesser de l’identifier au langage logique formalisé. La présentation catégorielle de la logique est beaucoup plus adéquate aux besoins contemporains d’une corrélation logico-philosophique.

Pour nous, nous assumerons que le vide est une réquisition de l’ontologie.

Sur la catégorie de négation

Que la négation soit onto-logique peut paraître immédiat : c’est à la fois un connecteur logique et un terme fondamental du discours philosophique.

Regardons-y de plus près.

La négation va être un opérateur logique décisif, parce que c’est sur cet opérateur logique que s’exerce la plus vive pression de la décision ontologique. La force de la négation va être tout spécialement affectée par le type de décision ontologique sous-jacent. Peut être précisée sa force disjonctive. Ce qui va graviter sur la question du statut du tiers-exclu. Les raisons sont nombreuses de l’importance extrême du tiers-exclu dans l’histoire de la philosophie, et dans l’histoire de la logique.[7]

On va appeler force disjonctive de la négation la question de savoir si le négatif est le seul Autre de l’affirmation. Ce qui se disjoint d’un état de choses, c’est sa négation et rien d’autre. C’est ce que dit le tiers-exclu : p ou ¬p (¬p est le seul Autre de p).

Le principe du tiers-exclu exhibe une force maximale du négatif. C’est ceci qui va requérir une décision ontologique : qu’a-t-on décidé sur l’être pour que la force disjonctive de la négation soit maximale ? Nous verrons que le tiers-exclu, en effet, est organiquement lié à ces décisions ontologiques qu’on peut identifier.

Si ce n’est pas le cas, il y a entre p et ¬p des modalités de p autres que la négation, éventuellement infinies. La négation est alors au plus comme un extremum d’altérité, un autre-limite. Là aussi, il y a des décisions ontologiques sous-jacentes qui vont organiser d’autres réquisitions ontologiques. Une ontologie comme celle de Deleuze est de ce côté ; d’ailleurs, Deleuze hait le négatif, toute idée que le négatif soit l’Autre unique.

C’est cela qui va nous donner le statut de la négation du point de vue ontologique. La négation est un peu le sismographe de la décision quant à l’être.

En réalité, tout va porter sur le statut de la différence. Selon que nous avons telle ou telle décision sur la différence, la force de la négation varie. Donc, nous sommes renvoyés à un rapport entre négation et différence, typiquement ontologique.

Autre question : la question de la double négation : ¬¬p p.

Il y a deux positions logiques extrémales : celle qui va affirmer que ¬¬p = p et celle qui va affirmer que ce n’est pas la même chose. C’est une discession originaire dans les démêlés entre philosophie et logique.

La question de la double négation, c’est la question de la capacité créatrice du négatif. Capacité créatrice et puissance disjonctive ne marchent pas forcément ensemble. Si ¬¬p = p, la puissance créatrice de la négation reste limitée. L’opérateur ¬ ne fait pas advenir autre chose que l’assertion initiale. Mais en ce point, la force disjonctive est maximale. Donc, si la force disjonctive est maximale, la force créatrice est atténuée. La topologie induite par la double négation est une topologie triviale, sans intérêt. Et inversement.

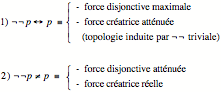
¬¬p va désigner un voisinage de p, topologiser p. Il y a un espacement, induit de p, par la double négation.

Il y aurait donc deux grandes options ontologiques sur la négation :

- L’une qui privilégie la force disjonctive, c’est-à-dire l’unicité de l’Autre d’une affirmation. Le vide est convoqué entre p et ¬p. Dans ce cas, la topologie de ¬¬ est sans intérêt. La négation n’induit pas d’espacement.

- L’autre pour laquelle la négation est avant tout une création possible, un espacement topologique nouveau, où la négation prescrit un lieu. Mais dans ce cas, on doit admettre une pluralisation déployée de l’altérité.

Comme nous le verrons, les décisions ontologiques sous-jacentes à ces deux sites sont essentielles, originairement. Un bon exemple serait de confronter sur ce point la décision parménidienne et la décision hégélienne : le fragment 8 de Parménide, et le chapitre sur l’Idée absolue à l’extrême fin de la Logique.[8] Si on confronte la décision parménidienne et la décision hégélienne, on voit bien que le point d’application de la décision, c’est la négation. Non pas que ce soit la négation qu’on décide, mais la pression de la décision s’exerce immédiatement sur la négation, au point d’en faire un impératif chez Parménide. Chez Hegel, c’est conserver à tout prix la capacité topologiquement créatrice de la négation (ce n’est pas pour rien que ce sont des figures).

II

Reprise

Les cinq concepts fondamentaux de l’onto-logie sont : l’infini, la différence, le vide, la négation, la décision.

Rappelons-en les points nodaux :

• la décision

On admettra que la logique adopte dans la pensée une position descriptive, corrélée à la notion générale d’univers possible, laquelle articule un principe de consistance et un principe d’extension.

Toute ontologie est, dans la pensée, au régime d’une décision fondatrice. Toute pensée a toujours déjà pris une décision quant à l’être. C’est la raison pour laquelle la question de l’ontologie n’est jamais à un régime programmatique.[9]

• le vide

C’est le point de suture à l’être de tout discours sur l’être. Le vide nomme le point où le discours sur l’être se capitonne à la décision.

• la négation

C’est l’opérateur logique fondamental, parce que c’est sur lui que s’opère immédiatement la pression de la décision ontologique, très particulièrement sur la force disjonctive de la négation.

• la différence

La grande question concernant la différence est la question du rapport entre global et local. Y a-t-il des différences purement qualitatives, c’est-à-dire des différences qui ne peuvent s’estimer que globalement ?

Une différence extensive est une différence qui se laissera toujours tester en un de ses points, dont il y aura un protocole d’évaluation local.

Quelque chose comme ça est à l’œuvre dans la différence entre l’épicurisme (atomistique), et le stoïcisme qui renvoie toujours à des inflexions sur la totalité.

La question de la différence va aussi se présenter comme question onto-logique. C’est la question : qu’est-ce qu’une localisation ?

Son élaboration comme question interne à la logique elle-même est une opération récente : celle de géométrisation de la logique. Dans la géométrisation de la logique, dans la traversée de la logique par la dialectique du local et du global, s’opère une logicisation de la question de la différence, en tant que finalement la question de la différence est celle de savoir s’il y a ou s’il n’y a pas des différences purement intensives.

L’objection de Bergson au positivisme est qu’il y a des différences non extensives : c’est le régime de la différence spatiale. Il y a une intrication interne de la durée qui fait que la différence n’est pas évaluable en l’un de ses points.

La reprise logique de cette question s’est faite récemment quand on a constaté que les lieux logiques nouent la question de la vérité à des réquisitions topologiques, jusqu’à donner sens à des vérités locales, et à des logiques des lieux. La question de la différence est donc bien un des points fondamentaux où la logique s’articule à la décision onto-logique.

Peut-être qu’un des apports les plus profonds de la théorie des topos porte sur ce point : dans ce qu’il y a de géométrique dans la logique elle-même.

Il y a des intuitions de Lacan très décisives sur ce point aussi : il faut une topologie pour rendre compte de ce qu’est le lieu subjectif, le sujet comme lieu et pas seulement comme syntaxe.

• l’infini

C’est une question clef. Tout le point est de savoir en quel sens c’est une question onto-logique.

Toute assertion d’existence concernant l’infini rétroagit sur le type de contraintes logiques admissibles. Il est certain que les différents types possibles d’assertion d’existence quant à l’infini entraînent des réquisits singuliers quant aux contraintes logiques opératoires.

Dans la grande logique, on a toujours su qu’une partie des contraintes logiques reçues comme naturelles n’étaient plus opératoires si on prétendait les appliquer à l’infini, à Dieu. Tout le vaste courant de la théologie négative a, en son cœur, la conviction que la ressource logique entre en défaillance aux abords de l’infini. Que la régulation du dire lui-même est inadéquate. Ce qu’on peut dire est toujours dans la forme du dire que ne pas. On peut dire de Dieu que ne lui conviennent pas les prédications logiques qui sont recevables pour toutes choses. Dieu est une soustraction, ou un trou, dans la logique. L’infini fait trou dans la logique : c’est un massif héritage de la théologie négative. Au bord de ce trou, il y a quelque chose qui touche à la négation. L’infini n’est pas ceci ou cela. Le trou dans la logique va être bordé par la négation. La négation est une fixation en effet de bord de la trouée de l’infini dans les dispositifs logiques. Ce qui signifie qu’il y a certainement une corrélation entre les assertions d’existence sur l’infini et la question de la force de la négation, le statut du négatif.

Ceci court jusqu’aux tentatives logiques les plus récentes. La querelle entre logique classique et logique intuitionniste est toujours simultanément une querelle sur la négation et une querelle sur l’infini.

Nous aurions l’intuition suivante : si on accepte des assertions d’existence fortes sur l’infini (Cantor, Descartes...), alors on va aussi admettre une force disjonctive de la négation assez radicale. Ceci n’est pas simplement intuitif, c’est ce point qui est ontologique. Inversement, les réticences sur l’existence de l’infini (de caractère intuitionniste ou constructiviste) s’accompagnent d’une théorie faible de la négation (rejet du principe du tiers exclu).

Il y a donc un lien entre les thèses sur l’infini et les thèses sur la négation.

Ce lien s’étend aux formulations logiques de type nouveau : par exemple, les formules lacaniennes de la sexuation présentent des opérateurs qui n’engagent pas la négation classique. L’opérateur du pas-tout est autre chose que la simple négation classique d’un universel :. Mais le pas-tout est quelque chose comme une négation, c’est un dire que non. Il y a certainement, dans cette entreprise de Lacan, la proposition latente d’une négation dont tout le problème est de penser qu’elle n’est ni la négation classique, ni non plus réductible à la négation intuitionniste :

«De ce qu’on puisse écrire pas-tout x ne s’inscrit dans Fx, il se déduit par voie d’implication qu’il y a un x qui y contredit. C’est vrai à une seule condition, c’est que, dans le tout ou le pas-tout dont il s’agit, il s’agisse du fini. Pour ce qui est du fini, il y a non seulement implication, mais équivalence. Il suffit qu’il y en ait un qui contredise à la formule universalisante pour que nous devions l’abolir et la transformer en particulière. Ce pas-tout devient l’équivalent de ce qui, en logique aristotélicienne, s’énonce du particulier. Il y a l’exception.[10] Seulement, nous pouvons avoir à faire au contraire à l’infini. Ce n’est plus alors du côté de l’extension que nous devons prendre le pas-tout. Quand je dis que la femme n’est pas-toute et que c’est pour cela que je ne peux pas dire la femme, c’est précisément parce que je mets en question une jouissance qui au regard de tout ce qui se sert dans la fonction de Fx est de l’ordre de l’infini.[11]

Or, dès que vous avez affaire à un ensemble infini, vous ne sauriez poser que le pas-tout comporte l’existence de quelque chose qui se produise d’une négation, d’une contradiction. Vous pouvez à la rigueur le poser comme d’une existence indéterminée. Seulement, on sait par l’extension de la logique mathématique, celle qui se qualifie précisément d’intuitionniste, que pour poser un «il existe», il faut aussi pouvoir le construire, c’est-à-dire savoir trouver où est cette existence». (Encore p.94)

Lacan nous dit :

1) Le pas-tout qui identifie la position femme ne doit pas être entendu comme la particulière aristotélicienne.

2) Si l’espace de référence est fini, il n’y a pas cette nouveauté, il faut être aristotélicien, la logique est classique. Si on est dans une décision ontologique finitiste, on est aristotélicien.

3) Il faut assumer que l’espace de référence est infini.

4) Si c’est infini l’espace de référence, la négation du tout ne nous indique aucune existence particulière. Elle nous indique une existence indéterminée. Une existence indéterminée, ce n’est pas exactement une existence, puisqu’une existence ça doit se construire. On va donc rester dans une objection indéterminée au tout.

Ce qui fait donc la singularité de la négation lacanienne, en l’espèce du pas-tout, c’est son caractère indéterminé. Donc, nous avons une négation affaiblie qui ne permet pas de conclure à l’Autre du tout.

Pour rénover la négation, y compris dans l’entreprise lacanienne, il faut passer par l’infini. On doit avoir une négation qui laisse quelque chose en suspens, nommément l’identité de l’exception. Ce qui se dira : « la femme n’existe pas».[12]

Il y a donc une corrélation entre la thèse ontologique sur l’infini, et la thèse sur la force de la négation. C’est ce qui légitimise que l’infini soit bien au lieu de l’onto-logie. Les décisions sur l’infini affectent le négatif.

Par ailleurs, on peut montrer qu’il y a une corrélation essentielle entre l’infini et la différence.

C’est un point sur lequel Hegel a énormément travaillé. Hegel est celui qui tente de penser jusqu’au bout la corrélation entre l’infini et la différence. En particulier entre infini, différence qualitative, et différence extensive. Il est celui qui tente de disposer la question de l’infini au regard de cette scission de la différence : le mauvais infini (procès de répétition), et le bon infini (récollection qualitative du mouvement même de la répétition).

Ce que Hegel va conclure, c’est qu’il convient d’appeler infini le pur mouvement de la répétition, ce qu’il y a de qualitatif dans toute insistance quantitative. L’infini va être le répétant dans la répétition. C’est pourquoi il va se donner comme l’essence du fini dans le mouvement de la répétition. La question de l’infini, c’est la question de : qu’est-ce qui insiste dans une insistance, qu’est-ce qui fait répétition dans ce qui se répète ? Qu’est-ce qui est absolument nouveau dans toute répétition ?[13] Cet élément de novation qui est le qualitatif de la répétition est le bon infini. Le mauvais est ce que le répété déploie à l’infini.

«L’infini donc qui dans le progrès infini n’a que la signification vide d’un non-être n’est en fait pas autre chose que la quantité». (Logique  - livre premier - section deux)

Ceci est le point de suture fondamental de toute la Logique. Il n’est pas possible de penser l’infini sans penser la différence de la différence, la différenciation de la différence, entre différence qualitative et différence intrinsèque.

Donc, l’infini est un nœud de tous les autres.

On y trouve la décision, parce que l’infini est toujours un point clef de toute décision sur l’être. On y trouve la négation, puisque toute décision sur l’infini affecte aussitôt la négation, et que toute décision de rénover la négation convoque l’infini. On y trouve le vide, parce qu’il n’est possible de penser l’infini sans un il y a pur. Et parce qu’on ne peut pas penser la répétition sans convoquer le vide (qu’est-ce qu’il y a entre ?). On y trouve la différence, parce que l’infini traite aussi de la différence de la différence.

Comment ces cinq concepts fondamentaux vont-ils être exposés et noués dans le cadre de la théorie des topos ?

Ils vont être réarticulés et noués dans quatre théorèmes : les théorèmes fondamentaux de l’ontologie. Ces quatre théorèmes vont nous servir d’armature et donc légitimer que la théorie des topos est bien ce à partir de quoi on peut éclairer aujourd’hui le nouage onto-logique.

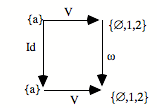
1) Le premier théorème fait nœud du vide, de la différence et de la négation de la façon suivante : on peut définir un univers où la différence a un statut local (topos bien pointé). Ce premier théorème est une caractérisation complète d’un topos bien pointé :

Si dans un topos, il y a unicité du vide, plus le fait que la logique du topos est classique (négation forte, réellement disjonctive), alors ceci est équivalent au fait que le topos est bien pointé (toute différence a un statut local).

vide négation forte la différence a un statut local

Cette corrélation est une corrélation mathématisable : ce théorème, on peut le démontrer.

2) Le deuxième théorème va faire nœud de la décision et de la négation.

- On va partir de l’élaboration interne à un topos de la notion de décision qu’est l’axiome de choix.

- On va démontrer que tout topos qui admet l’axiome de choix est classique.

(On peut montrer que l’axiome du choix engage quelque chose de l’infini et de la décision).

(infini, décision) (négation)

3) Le troisième théorème va faire nœud des deux dimensions possibles de la notion d’infini que nous venons de voir. Il va faire nœud de l’infini comme récurrence et de l’infini comme infini actuel (en termes hégéliens, du mauvais et du bon infini). Cela va se dire : tout topos qui admet un opérateur de succession en position universelle (un objet nombre naturel) admet en fait un objet intrinsèquement infini.

On n’aura pas seulement des successions, mais des schèmes de la succession, dans le topos, un diagramme de la succession comme telle. Pas simplement la chose, mais une instance du concept de la chose. La transcendance est éliminée, de façon spectaculaire. La logique est inscrite dans l’univers, elle y est localisable.

L’univers des topos nous montrerait que s’il y a du mauvais infini, il y a du bon. Ce qui est la conviction hégélienne.

4) Le quatrième théorème — le plus profond, le plus moderne, et le plus difficile — va faire nœud de la topologie de la question de la différence et de la question de la négation.

Il se dit : la topologie de la double négation permet d’extraire de tout topos un sous-topos classique.

Par quoi nous faisons une corrélation fondamentale entre différence, topologie de la différence et question de la négation.

Nous allons examiner maintenant l’investigation de l’infini dans sa présentation catégorielle.

Il y a trois approches essentielles de la question de l’infini, d’un point de vue strictement consensuel :

1) Par la question de l’indéfini, que Hegel reprend sous le nom de mauvais infini. C’est l’abord de l’infini à partir de l’opération de succession. C’est l’approche qui s’enracine dans l’idée de répétition : progrès à l’infini.

2) L’approche purement axiomatique ou opératoire : fixer des opérations telles qu’en réalité l’espace d’exercice de ces opérations sera nécessairement infini : ce qui se passe si on présente les nombres entiers sous la forme des axiomes de Peano. Au cœur de ces opérations, on va trouver le principe de récurrence ; une opération qui ne va fonctionner que dans un espace infini, mais sans avoir à le spécifier. L’infini reste implicite.

3) La tentative de définition intrinsèque.

Il y a des liens variés entre les trois approches.

Si on aborde cette question, on va rencontrer :

• La question de ce qu’est une itération telle que rien ne la borne (logique du “encore” : c’est toujours “encore” possible). Si on regarde de près cette question de l’opérateur de succession, on voit trois exigences :

- de point de départ : il faut un point fixe d’où ça part. Il y a solidarité du principe logique du encore avec un principe minimum de commencement ;

- un opérateur de succession : s, l’inscription de ce qui opère encore ;

- une nouveauté à chaque pas (pour que ça ait trait à la question de l’infini).

Ce qui importe ultimement dans la répétition, pour autant qu’elle touche à l’infini, c’est que quelque chose y est constamment nouveau. Sinon, c’est la stagnation.

Par exemple, supposons que le point de départ est la marque du vide Ø, l’opérateur s, si on applique l’opérateur au point de départ :

(Ø), s(Ø), s(s(Ø)) ....n fois.

Cette affaire ne touche à l’infini que si chaque terme s’avère différent des autres. On fait la même chose, mais ce qui est fait n’est pas la même chose ; on a une production d’autre par le même. L’infini serait déjà ça : “l’outrepassement”, très précisément chez Hegel. Le même se répète, mais quelque chose franchit sa propre limite.

• S’agissant de l’identification axiomatique, c’est une caractérisation prédicative de la succession. On y retrouve le commencement, et l’opérateur. Mais on a la caractérisation de la récurrence.

Si on a une propriété P : P(O),

et si : ,

alors :

Ce qu’il y a de nouveau, c’est que le quantificateur “pour tout” totalise, ce qui est un saut par rapport à la simple idée de succession. C’est ce saut à l’universel qui est le principe de récurrence, le principe d’induction.

Dans cette explicitation axiomatique, il y a un pas en plus, qui est un pas de totalisation. Non seulement la succession insiste, mais il y a sens à dire : pour tous les termes de la succession.

C’est le principe d’induction, en tant qu’il enveloppe l’idée d’une récollection, qui singularise cette approche par rapport à la précédente.

L’approche axiomatique est intermédiaire entre la première et la troisième approche. On peut dire qu’il y a là une totalisation indéterminée. Il n’y a que l’inscription de ce tout, il n’y en a pas de détermination. L’universel n’est pas la même chose que la totalité : on ne se donne pas le tout de ce tout.

• S’agissant de la troisième, elle vise à thématiser l’infini. Il y a une caractérisation intrinsèque de l’infini qui peut se faire par voie positive, ou par voie négative :

- Par voie positive : on dira qu’un ensemble est infini s’il existe une correspondance biunivoque entre lui et une de ses parties strictes (Dedekind). Ceci remonte à de très anciennes remarques, en particulier de Galilée. C’est une définition existentielle et affirmative. L’infini est renvoyé à l’existence d’une figure de rapport interne à l’ensemble.

- Par voie négative : poser comme infini un ensemble qui n’est pas fini ; il n’y a pas de correspondance biunivoque entre l’ensemble I et un ordinal fini.

Cette fois, c’est une négation d’existence. Il est déclaré infini expressément parce qu’il n’est pas fini. Nous trouvons là aussi une corrélation entre infini et négation. La définition de Dedekind est sans négation.

Les deux définitions donnent des définitions très différentes du fini :

- La première : il n’y a pas de correspondance biunivoque entre I et EI. C’est un ensemble Dedekind-fini. Là, l’idée de l’infini est plus claire que celle du fini, comme le pensait Descartes. Chez Dedekind, c’est l’infini qui est le principe clair, et le fini qui n’en est que l’envers négatif.

- Dans l’autre définition : le fini est dans une correspondance biunivoque avec un nombre entier. C’est le fini naturel. C’est fini quand on peut compter.

Est-ce que Dedekind-fini et fini-naturel, ça coïncide ? Est-ce que c’est les mêmes ?

On ne peut démontrer qu’ils sont la même chose qu’en utilisant l’axiome du choix. Ce qui prouve que cette identité n’est nullement triviale. Ce qui illustre que le fini est une idée des plus compliquées. Cela, les topos le montrent. Et tout ça est sous la dépendance de l’axiome du choix, c’est-à-dire d’une définition sur l’infini. Il n’y a pas d’originarité claire du fini. Le fini est obscur. Surtout, il est équivoque, intrinsèquement.

Que va nous apporter l’approche par les topos sur cette question ? Elle va nous montrer la connexion de ces trois approches, et c’est fondamental. Elle ne va pas nous montrer qu’il y a une connexion, mais où ça se joue. Elle va élucider la fibration du concept d’infini, son nouage interne. Elle va nous montrer la logique sous-jacente à toute décision concernant l’infini.

Le point de départ va être de capturer l’idée même de succession. L’itération exige que l’on parte d’une action identique, ce qui permet de la recommencer. Le point de départ va être un élément de a :

Comment va se trouver capturé le concept de répétition ?

Dans un topos, l’universel se présente d’abord comme une singularité. Il va falloir qu’il surplombe toute répétition comme s’il la subsumait :

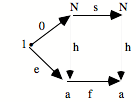
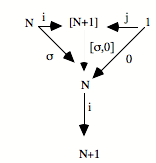
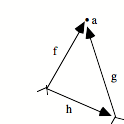
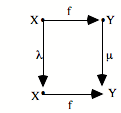
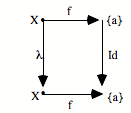
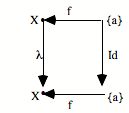
Il y a de N vers a une action h unique qui fait commuter le diagramme : h o 0 = e

h o s = f o h.

La flèche répétitive f est capturée par s à l’aide des corrélations h. s va être une répétition telle qu’elle capture toute autre répétition.

Si on a cela, tel que pour tout autre diagramme de type répétitif on a l’effet de capture des flèches uniques de N vers a, on dira qu’on a une répétition en succession universelle.

N s’appelle un objet nombre naturel.

C’est un protocole de succession tel qu’il donne mesure de tout autre. C’est pourquoi, on peut dire que ceci :

est le diagramme de la succession. Le diagramme de la succession n’est lui-même qu’une succession. Mais une succession qui est en position de capture par rapport à toute succession, y compris elle-même.

Quand nous avons cela dans un topos, nous avons un diagramme conceptuel de ce que c’est qu’une succession , c’est-à-dire de ce que c’est que l’infini appréhendé à l’infini.

Les étapes suivantes vont être :

- Montrer que c’est un vrai progrès à l’infini, c’est-à-dire qu’il y a constamment du nouveau.

La clé du raisonnement est de démontrer que s est un monomorphisme, c’est-à-dire un conservateur de différences.

- Montrer que N est intrinsèquement infini.

Il va falloir définir un objet infini. N est isomorphe à N+1.

Nous allons unifier le mauvais infini et le bon infini.

III

On a proposé la dernière fois une approche générale, largement informelle. Le point principal en est trois approches du problème de l’infini, c’est-à-dire trois protocoles de pensée qui tentent de constituer l’intelligibilité de l’infini, ne se clôturant pas par une définition explicite de l’infini, c’est un autre problème. Nous reviendrons sur cette question très importante, qui est la question de savoir dans quelle mesure le problème de l’infini est lié au problème d’une définition de l’infini.

Entre parenthèses, cette question est philosophiquement très importante parce que, pour part, dans la tradition théologique, il y a une tentation traditionnelle de poser que l’infini est proprement l’indéfinissable. Ça, c’est à proprement parler la question de la transcendance. Si infini est en réalité un nom pour la transcendance, il fonctionne toujours comme un nom pour ce qui excède les ressources de l’intellect fini. S’il est un nom de ce qui excède les ressources de l’intellect fini, il n’est pas immédiatement appréhendable par les opérations de cet intellect. C’est une tradition à la fois philosophique, théologique, mais qui a aussi son occurrence mathématique qui est de poser que l’infini c’est toujours l’au-delà de toute opération préalablement donnée. Pour prendre un exemple élémentaire, vous pouvez dire : j’ai une opération de succession, de répétition, d’itération, j’ai un champ d’insistance, il y a toujours du encore, mais ne sera proprement infini que ce qui sera inaccessible pour cette opération. Ce qui succède est toujours un terme fini. Il y a une tradition conceptuelle qui posera l’infini comme précisément le point qui est inaccessible pour une opération préalablement donnée, de répétition, d’itération..., donc une opération du mauvais infini. L’infini proprement dit sera précisément ce qui sera au-delà du mauvais infini. Il est assez caractéristique à cet égard qu’en théorie des ensembles, on définisse précisément des cardinaux inaccessibles, non mathématiquement constitués, pour des figures de transcendance.

Ceci pour dire que la question de savoir ce qu’est une définition de l’infini est toujours une question ambiguë. Peut-être que, par exemple, l’infini est proprement ce qui est inaccessible à toute procédure définitionnelle. Voilà pourquoi les trois orientations dont nous parlons concernant l’infini ne sont pas forcément et immédiatement soldées par des définitions explicites, mais constituent plutôt des lieux d’intelligibilité possible de la notion.

Ces trois approches étaient, je le rappelle :

- la classique approche par l’indéfini, c’est-à-dire au fond : il y a un opérateur dont on peut répéter l’action, et dont on peut la répéter sans qu’un terme soit fixé de façon immanente à cette opération ;

- la possibilité opératoire, c’est-à-dire disposer d’une opération telle que son champ d’exercice ne peut qu’être infini, aucun champ fini ne peut tolérer que cette opération-là y soit possible. Là, c’est l’opératoire qui prescrit la dimension sous-jacente de ce sur quoi il opère. Remarquez que, dans ce cas, vous n’engagez pas une définition explicite de l’infini, vous n’avez pas besoin de thématiser l’infini ;

- et puis, il y a les tentatives de donner un concept. Nous avions cité comme exemple la fameuse décision de Dedekind qui est qu’un ensemble est infini s’il existe une correspondance biunivoque entre lui et une de ses parties. Ce qui veut dire qu’un ensemble est infini lorsqu’il viole le principe selon lequel le tout est plus grand que la partie.

Le but qui est le nôtre, c’est de montrer que la saisie de ces notions dans la théorie des topos permet de penser leur corrélation interne, permet quasiment de voir ce qui circule pour la pensée entre l’indéfini, l’opératoire, l’infini intrinsèque, d’exhiber des liens, en termes d’univers possibles, de l’intérieur d’un univers décidé. Ceci s’effectue sans qu’on ait jamais besoin, à proprement parler, de thématiser l’infini, d’en donner une définition explicite.

Ce qu’il faut bien comprendre c’est quelle est la nature exacte de ce que nous allons faire. Ce que nous allons faire, c’est fixer les conditions sous lesquelles on peut dire qu’un univers contient de l’infini. Laissons de côté la question de savoir si l’univers, lui, est ceci ou cela. Comme toujours, la démarche est descriptive et immanente, et donc on va dire : s’il y a telles choses dans un topos, si tel système de conditions est réalisé, alors on pourra convenir de dire que ce topos est tel qu’il contient de l’infini. Par conséquent, l’infini sera localisé. Il ne s’agit pas ici de se prononcer sur la taille, si je puis dire, de l’univers. Cela, c’est une démarche ensembliste. On ne va pas s’engager là-dedans, on va simplement dire : voilà où on peut localiser, sous certaines conditions, l’infini dans l’univers. Cela veut dire qu’on aura des réseaux d’actions singuliers qu’on va définir, typifiants, et éventuellement, qu’on aura dans l’univers un objet dont il y aura un certain sens à dire qu’il est infini.

La démarche en pensée ne consiste pas à se demander si l’univers référentiel de la pensée est infini ou n’est pas infini — cela n’a pas de sens immédiat — ; comme toujours, il s’agit de savoir où l’on trouve l’infini dans un univers possible et qu’est-ce que ça veut dire que de l’y trouver.

Le point de départ est de capturer de façon définitionnelle la notion de succession.

Première question : comment peut se présenter, dans un univers de type topos, une action telle qu’on puisse la répéter, la faire, puis la refaire, puis la refaire encore, et ceci sans limite assignable. Cela c’est l’élément du même, qui dit que, d’une certaine façon, une répétition, c’est une même opération qui cependant produit, incessamment, de l’autre. L’opération est à chaque fois la même, c’est l’opération du plus un, et cependant le terme engendré, si je puis dire, par la répétition est incessamment différent. C’est cela qui nous donne le schème abstrait de l’indéfini.

Nous avions esquissé cela la dernière fois. Nous avions dit : pour qu’une action puisse se succéder à elle-même, il y a une condition sine qua non, c’est que le point d’arrivée de cette action soit le même que son point de départ, puisque sinon, vous ne pouvez pas répéter. Il s’agit d’une flèche dont la source est également la cible. Cela, c’est la matrice élémentaire, en termes catégoriels, de la répétition.

Par ailleurs, nous avions remarqué que, dans la procédure de l’indéfini, il faut que le point de départ soit fixé. Il faut qu’il y ait un point de départ assignable qui fixe le début de l’itération. Là, nous conviendrons que le point de départ doit être un point de départ élémentaire, et un élément d’un objet, c’est une flèche de 1 vers cet objet. [14]

Si on récapitule tout ça, on voit que le schème catégoriel de l’itération est intégralement représenté par ce diagramme :

Mais ce qui, pour l’instant n’est pas garanti, c’est que la répétition de s produise toujours du nouveau. Il se peut très bien que s soit telle qu’en la recommençant, votre action combinée vous redonne l’action élémentaire du départ. Ceci nous indique la possibilité de la répétition, donc la possibilité d’itérer le même, mais pour l’instant ne nous prescrit nullement que cette itération du même engendre du nouveau.

Donnons tout de suite un exemple. Nous connaissons parfaitement une des flèches de a vers a, c’est l’identité de a, qui existe obligatoirement associée à tout objet a, qui est ce par quoi a, si je puis dire, se rapporte à lui-même. Or, vous pouvez combiner ida avec ida ; mais : ida o ida = ida ; par conséquent, on a là une itération qui ne produit rien de nouveau. Ce n’est pas parce qu’on a une possibilité d’itération que l’on a nécessairement la productivité de l’itération. Il faut donc distinguer ce que l’on peut appeler les répétitions stagnantes — qui peuvent aussi être des répétitions circulaires —, et les réelles répétitions indéfinies dont il sera demandé ou exigé qu’elles engendrent à chaque pas une nouveauté.

Donc, pour l’instant ce que nous avons c’est simplement comment représenter dans un univers toposique le schéma élémentaire de l’itération.

Quand il y a cela, dans un topos — et il y a toujours nécessairement des objets tels qu’ils ont un élément et une flèche intérieure —, ce qu’on peut simplement dire, c’est qu’il y a de la répétition possible. La notion d’itération et d’action est présente dans le topos, sous la forme d’un certain nombre de cas. Mais c’est tout.

C’est ici que nous allons utiliser quelque chose de plus intéressant que cela, qui est la capacité de la pensée catégorielle et toposique de présenter, y compris sous forme de diagramme, non pas seulement un cas, mais le concept du cas. C’est-à-dire pas seulement ceci qu’il y a une itération possible, mais quelque chose qui exprime universellement cette possibilité.

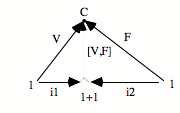
En pensée catégorielle, la notion de limite exprime une position universelle par rapport à une certaine configuration. Vous avez des configurations, et vous avez quelque chose qui, par rapport à toutes les configurations de ce type, est en position de type universel. La position universelle combine, assez classiquement, une espèce de subsumption, d’une part, et un principe d’unicité, de l’autre. Il y a de l’un, dirait Lacan, dans cette affaire de l’universel. C’est cette combinaison de subsumption et d’unicité qui détermine la notion d’universel.

Ce qui est caractéristique ici, c’est que cet universel est présenté. La limite est elle-même une configuration dans le topos. Ce qui veut dire que l’universel est lui-même localisé. On peut dire que l’universel est lui-même présenté comme singularité. Ce qui a fait dire qu’il y avait dans la pensée catégorielle quelque chose d’immédiatement dialectique, d’immédiatement hégélien, le fait que l’universel se présente sous la forme d’une singularité diagrammatique identifiable dans l’univers dont il s’agit. Donc, cette subsumption, cette unicité, ce ne sont pas une transcendance extérieure, ce ne sont pas des idées platoniciennes, ce ne sont pas des schèmes transcendantaux, ce n’est rien de tel. Ce sont des singularités présentes dans le topos, mais qui opératoirement sont en position et de subsumption et d’unicité.

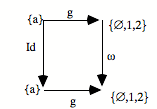
Le problème est de savoir comment, étant donnée la configuration de succession représentée par n’importe quel diagramme de ce type dans le topos, nous identifions ce genre de diagramme à l’idée de répétition avec point de départ. Comment saisir, avec subsumption et unicité, c’est-à-dire en limite, à sa limite, cette configuration ? Forcément ce qui saisit en subsumption, donc de façon universelle, une configuration de ce type est une configuration de ce type. Cela, c’est une démarche essentielle.

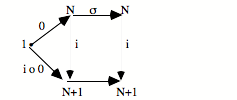
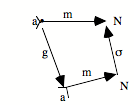
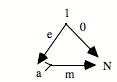
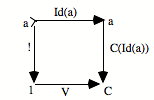
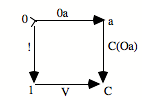
Comment vont s’effectuer la subsumption et l’unicité ? Comme dans tous les cas limites, cela va se donner dans le fait qu’il existe une flèche unique de N vers a qui fait commuter le diagramme. Cela va se donner sous la forme suivante : le triangle commute et le carré commute.

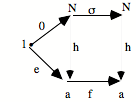
Le triangle commute : h o 0 = e

Le carré commute : h o s = f o h

Ces deux équations expriment que le carré commute, que le triangle commute, et donc que tout le diagramme commute. Le fait que ça commute nous donne un système de saisie ou de subsumption. L’élément e particulier, qui est le point de départ de la configuration répétitive, ici, va être «capturé» par l’élément 0 qui est le point de départ de l’universel. De même, l’opérateur f va être capturé par s, c’est-à-dire l’opérateur universel, avec l’aide du h qui est l’action de saisie, l’action de subsumption. On peut dire que h, c’est ce par quoi la succession s saisit la succession f.

Il y a plusieurs métaphores possibles : saisir, agir, voir... L’important est de retenir que par h, la succession f est subsumée sous la succession s. De même, par h, le point de départ élémentaire e est subsumé sous le point de départ 0. Quant à l’unicité, elle est présente sous la forme qu’h est unique. Il n’y a qu’une manière d’opérer la subsumption. Cela signifie que le :

est en position universelle pour la subsumption, cela saisit toute succession dans les conditions où l’opérateur de succession est unique.

Je dirai — c’est un peu une métaphore —, mais je dirai volontiers en tendant un peu les choses, que ceci nous donne à l’intérieur du topos, quand ça existe, le concept de la succession, et non pas simplement une succession. Nous aurions là quelque chose qui est la position conceptuelle de la répétition. Mais encore une fois, si cette limite existe, elle sera présente dans le topos. C’est pourquoi vous aurez, dans le topos, non seulement des successions diverses, variées, nombreuses, mais aussi le concept de la succession, en position limite de toutes les autres. Donc, ça nous donne une intériorisation structurale de l’universel.

Dans un topos où cette limite existe, c’est-à-dire où pour toute itération, pour tout diagramme répétitif de ce genre, N et s capturent la répétition, on dira qu’on a, dans le topos, un ONN, c’est-à-dire un objet nombre naturel. L’objet nombre naturel c’est N. Ici, objet nombre naturel ne renvoie à rien d’autre qu’au concept de la répétition à point de départ. Il faut éloigner ici toute intuition du nombre. Ceci ouvre à la possibilité que soit appelé nombre, dans un topos, quelque chose qui a peu de rapport avec notre intuition du nombre.

Donc, supposons que nous avons ceci :

un objet N qui a un élément, une action de N vers N, qui est en position universelle sur toute répétition possible.

Nous allons maintenant regarder ce qui se passe s’il y a cet objet.

Tout le point va être sur cette question de la productivité. Vous voyez que ça n’aura rapport à l’infini, même sous la forme de l’indéfini, que si, lorsque vous répétez s, vous engendrez du nouveau. Pour s’assurer qu’il y a toujours du nouveau, qu’est-ce qu’il faut montrer de manière un peu générale ?

Considérons une répétition de s, n fois :

Si vous voulez être sûrs que sn vous donne quelque chose de nouveau par rapport à tout ce que vous avez déjà produit avant, cela veut dire qu’il faut que sn soit différent de s, de s2, de s3, ... de sn-1.

On peut résumer cela : s ≠ sq, pour q < n.

Si on démontre cela de manière générale, quels que soient n et q, on aura notre affaire.

C’est une idée très importante, philosophiquement. C’est l’idée que, dans l’indéfini, dans l’idée d’une opération qui se répète indéfiniment, il n’y a présence de l’infini, même en un sens dégradé ou mauvais, comme dirait Hegel, que si le même répété produit de l’autre. C’est cela que nous exigeons...

Le mauvais infini, c’est une dialectique du même et de l’autre. L’opération est la même, mais les termes produits par la répétition de cette opération sont incessamment autres.

Nous allons démontrer que s’il y a un objet nombre naturel, c’est-à-dire une saisie universelle de la répétition, un concept de la répétition, alors il y a en effet mauvais infini : sn ≠ sq.

Pour démontrer ce point, qui est nodal, nous allons assumer un lemme qui se dit de la façon suivante : s’il y a un objet nombre naturel, il existe une flèche r de N vers N qui a les deux propriétés suivantes : r o 0 = 0, et r o s = idN

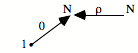
Qu’est-ce que c’est que cette flèche r ? C’est la fonction prédécesseur. Supposons que, dans les nombres, vous passiez de 1 à 2 par la fonction successeur. La fonction prédécesseur est une fonction qui va aller dans le sens contraire.

Donc la fonction arithmétique du prédécesseur obéit exactement à cette propriété. Le prédécesseur annule la succession. Vous passez au suivant, et si vous faites le prédécesseur, vous passez à l’identique.

Et elle obéit à r o 0 = 0, pourquoi ? Parce qu’il n’y a pas de prédécesseur de 0. Si vous lui appliquez la fonction, vous tombez sur lui-même parce qu’il n’y a rien avant.

Donc, vous retrouvez la propriété chaque fois qu’il y a un nombre naturel dans un topos. Cela veut dire qu’il y a la fonction prédécesseur.

Il y a une petite remarque à faire, c’est que la démonstration de l’existence de la flèche prédécesseur n’est pas triviale. Il faut démontrer pas mal de choses avant. C’est pour ça que je ne la fais pas, pour gagner du temps.

Maintenant, nous allons faire un deuxième lemme, c’est que, de l’existence de r résulte que s est un monomorphisme.[15]

Un monomorphisme est un conservateur de différences.

Supposons que : s o f = s o g

Il en résulte que : r o s o f = r o s o g

Mais r o s, par définition, c’est l’id N.

Par voie de conséquence, f = g.

Ce qui veut dire que l’opérateur universel de succession conserve les différences. Ça ne va pas pouvoir retourner au même, puisque ça conserve les différences. Donc, à chaque fois qu’il va y avoir des différences, elles vont devoir persister, et donc vous ne pourrez pas en répétant s, les annuler et reproduire de l’identique. C’est le point clé. A partir du moment où vous avez démontré que s est un conservateur de différences, il y a tout lieu de penser que ce n’est pas en le répétant qu’on va revenir à l’identique. Parce que chaque fois qu’on va cumuler une différence, il va falloir qu’elle se conserve. Et donc, vous allez forcément aller de différence en différence, c’est-à-dire que s va être différenciant parce qu’il ne peut pas être identifiant.

Comment va-t-on procéder ?

On va remarquer d’abord, ça va être notre troisième lemme : si m est un monomorphisme, mn l’est aussi.

C’est trivial. Vous voyez qu’un monomorphisme, c’est quelque chose qui peut se simplifier.

Ce qui veut dire, pour reprendre notre problème de tout-à-l’heure, que sn et sq sont des monomorphismes, puisque s est un monomorphisme. Donc, on a quelque chose qui conserve la différence. Ce n’est pas en répétant, qu’on va faire disparaître cette capacité à conserver la différence.

Notre but, c’est de démontrer que sn ¹ sq.

On va supposer que sn = sq, et on va démontrer que ce n’est pas possible.

Si sn = sq, sn o 0 = sq o 0

n > q ; donc il existe (n - q)

On peut donc écrire sq o sn-q o 0 = sq o 0

sq est un monomorphisme, donc on peut l’enlever.

Donc : sn-q o 0 = 0

L’idée va être de mettre du r devant, pour arriver à du s. Les r, quand on les met devant les s, c’est comme si on les supprimait parce que ça donne de l’identique.

r n-q-1 o sn-q-1 o s o 0 = r n-q-1 o 0

s o 0 = r n-q-1 o 0

Or : r o 0 = 0

Donc : s o 0 = 0

On aboutit à ceci : si sn = sq pour q < n, alors cela veut dire que s o 0 = 0, de façon absolument générale.

Évidemment, cela veut dire que s’il y a une boucle, c’est qu’il y a une boucle dès le départ. Dès votre première application de l’opérateur, vous êtes stagnant, vous ne produisez rien d’autre que le point de départ. En langue naturelle, ça se dit : dans les conditions de définition de s et de n, si c’est fini, s’il y a une boucle, si ça ne produit pas incessamment du nouveau, alors en réalité, ça n’en a jamais produit. Cela résulte de ce que s est un conservateur de différences. Intuitivement, cela veut dire que si à un moment donné il n’y a plus de différence, c’est qu’il n’y en a jamais eu.

Il nous faut encore montrer que s, dans un topos, ne peut pas être stagnant.

Nous allons maintenant supposer que s o 0 = 0, et voir ce que ça donne. C’est là qu’il va bien falloir en montrer une, de différence !

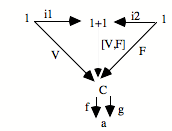
On est dans un topos. Et, dans un topos, nous connaissons plusieurs schémas de répétition. En particulier, celui-ci : un élément de l’objet central, qui existe nécessairement, est faux, et une flèche de l’objet central vers l’objet central, qui existe nécessairement, est la négation.[16] Nous savons que, dans un topos quelconque, dès lors qu’il y a un objet central, il y a une flèche de négation. Nous savons aussi qu’il y a une flèche faux qui est un des éléments de C. Les éléments de C sont les valeurs de vérité du topos. Il y a des topos où il peut y avoir une infinité d’éléments de C. Cela veut dire qu’il y a une infinité de valeurs de vérité. En tout cas, il y a le vrai et le faux, ça c’est sûr.

Mais ça, c’est un schème de répétition.

Par conséquent, s’il y a un objet nombre naturel, il faut qu’il subsume ça....

Supposons que s o 0 = 0. Supposons qu’il y ait stagnation. Nous allons voir que c’est incompatible, sauf dans un cas qui est le cas où le topos est dégénéré.

C’est un calcul qu’on peut faire de plusieurs manières :

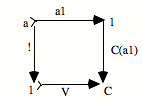
¬ o h o 0 = ¬ o f

Le carré commute.

Donc ¬ o h = h o s

¬ o f = V

Mais nous supposons que s o 0 = 0. Donc, nous avons : h o 0 = V

Mais h o 0 = F, parce que le triangle doit commuter.

Par conséquent, si s o 0 = 0, on a : le faux est égal au vrai. Et si le faux est égal au vrai, le topos est dégénéré. Il est réduit à un point.

C’est un théorème remarquable ; on le démontre. C’est peut-être la seule démonstration que je connaisse du fait que le faux est différent du vrai. Après tout, que le faux soit différent du vrai, c’est une vieille question philosophique. Comment se fait-il qu’il n’y a pas que le vrai ? ... Dans un topos, il est démontré qu’il faut que le faux soit différent du vrai pour qu’il y ait de la différence, tout simplement. Dès qu’il y a de la différence, et pas seulement un point, il faut que le faux soit différent du vrai.[17]

Nous voilà maintenant un peu au bout de nos peines. Si le topos n’est pas dégénéré — on va remonter la chaîne —, c’est-à-dire s’il y a ne fût-ce qu’une différence dans l’univers possible envisagé, si tout n’est pas rabattu dans l’indistinction de l’Un, alors le vrai est différent du faux, alors s o 0 ≠ 0, et alors sn ≠ sq pour n > q.

Donc, nous voici en possession de la conclusion : s’il y a un objet nombre naturel, dans un topos, ce qui veut dire — et cela est peut-être le point le plus difficile à penser — s’il y a du nombre dans un univers possible pour la pensée — le fait qu’il y ait l’objet nombre naturel veut simplement dire : dans cet univers possible, il y a du nombre, sous cette forme élémentaire essentielle qui est un concept de la succession —, alors il y a nécessairement de l’indéfini, c’est-à-dire de l’incessante productivité, du nouveau. Ce qui veut simplement dire ceci : si vous avez sn, vous avez répété n fois l’opération, vous êtes sûr qu’en la répétant n+1 fois, ce sera encore nouveau, non obtenu précédemment.

Appelons-le le mauvais infini, et notre théorème est le suivant : S’il y a un concept de la succession, alors il y a nécessairement du mauvais infini.

Reste maintenant à se demander si nécessairement il y a du bon.

...

La totalité de ce qui est dit depuis le début présuppose toujours qu’on est à l’intérieur d’un topos. On montrerait sur un certain nombre de points qu’on en a absolument besoin. En particulier, vous remarquerez un point très important c’est que nous avons convoqué l’objet central, la négation et le faux pour boucler notre démonstration. Ce qui veut dire que pour établir la productivité du nombre, on a besoin de la machinerie logique. Après tout, l’objet central, la négation, le faux, la vérité, c’est vraiment la logique immanente du topos. Nous reviendrons sur ce point, parce que ce point engage la question de la corrélation entre infini et logique. Là, sous une forme que nous rencontrons, qui n’est pas encore élucidée, sur laquelle nous reviendrons, qui est que pour passer de «il y a le concept de la succession» à «c’est le mauvais infini», nous avons eu besoin de recourir au fait qu’il y a dans le topos des opérateurs proprement logiques.

Cela, c’est une question philosophiquement extrêmement intéressante et profonde qu’on pourrait dire ainsi : qu’est-ce qu’il y a de proprement logique dans le concept d’infini ? Le concept d’infini, c’est un concept théologique, c’est un concept philosophique, c’est certainement un concept mathématique. Là, nous touchons, comme toujours lorsque nous analysons en termes de topos, une dimension supplémentaire : qu’est-ce qui convoque la logique dans cette question d’infini ?

C’est un point très intéressant. On peut, par exemple, se demander si l’infini cartésien, le Dieu de Descartes, n’est pas par certains côtés fondamentalement un opérateur logique. C’était la position de Pascal. Pascal disait : le Dieu de Descartes, il en a besoin à un moment donné, dans un protocole de démonstration, et après, on n’en entend plus parler. Et donc, en réalité, le fond véritable de la position de Pascal sur le Dieu de Descartes, c’est la conviction que ce Dieu n’est pas un Dieu, parce qu’au lieu d’être d’abord et avant tout une existence, il est un opérateur.

Et si on prend un autre exemple tout-à-fait différent, chez Lacan, la question de l’infini est aussi tirée, de toute évidence, entre une fonction d’opérateur, requise pour que finalement fonctionnent les formules de la sexuation — il faut que quelque chose comme l’infini fonctionne pour qu’il y ait réelle opérativité du quantificateur pas-tout —, et puis d’un autre côté, une répugnance de Lacan à admettre que ça puisse être une existence, autre chose que strictement cet opérateur. De là, ses efforts tout-à-fait singuliers pour montrer que l’infini ce n’est qu’un opérateur d’inaccessibilité, et que le nombre 2 est déjà infini.

Cette question de savoir quelle est la fonction purement logique de l’infini, c’est une question très importante. Là, on ne l’a pas vraiment traitée, sauf qu’on a constaté au passage que pour désancrer la répétition (nouvelle), c’est-à-dire assurer la constante altération des répétitions successives, c’est-à-dire le pouvoir différanciant de la répétition, pour garantir cela, dans le protocole de la démonstration, on en a appelé à des configurations purement logiques.

Ceci pose la question de savoir dans quelle mesure l’infini est impliqué dans le logique, ou le logique dans l’infini, et qu’est-ce que tout cela signifie.

Nous avons gagné le concept de succession tel qu’il se donne dans un topos. Il y a, dans ce cas, effectivement mauvaise infinité, au sens où il y a effectivement incessante production de différence. La différenciation n’est pas bornée. Si vous réitérez s, vous aurez une opération nouvelle par rapport à toutes celles que vous avez obtenues antérieurement.

Peut-on passer à l’infinité intrinsèque ? C’est-à-dire quelque chose qui ne serait pas de l’ordre du “encore nouveau” qui est le point où nous en sommes. Nous sommes passés de l’universalité de la succession au toujours encore nouveau. Et nous n’avons toujours, pour l’instant, garanti aucune infinité intrinsèque : s(n), ça reste toujours fini. C’est bien pour ça que Hegel l’appelle mauvais, cet infini. C’est la possibilité de toujours passer outre, mais vous n’avez pas de récollection infinie de la chose.

Le problème, c’est que la définition de l’infini intrinsèque que nous avons donnée, elle est strictement ensembliste. Nous avons dit : un ensemble est infini, s’il y a une correspondance bi-univoque entre lui-même et une de ses parties. Notre problème, c’est de savoir en quel sens on pourrait soutenir que l’objet N — celui qui supporte la position d’universalité — peut être considéré comme infini. L’objet N, ce n’est pas un ensemble. C’est une lettre, strictement, déterminée par les actions qui l’ont pour source ou qui l’ont pour cible. N, ça n’a pas d’intérieur. Alors, comment parler de la dimension de N ?

L’idée directrice intuitive est la suivante. On peut prendre l’intuition de Dedekind un peu autrement, sous une forme d’ailleurs tout-à-fait pascalienne[18], et qui est la suivante : au fond, est infinie une chose telle que si on y ajoute quelque chose, elle reste pareille. Ça a des racines théologiques, ça, parce que la question a toujours été de savoir ce qui arrivait à Dieu quand il créait le monde. Il créait quelque chose en plus ; est-ce que cet en-plus rétroagit sur lui de telle sorte que ça affecte ou non son infinité ? La réponse est non. Dieu n’est pas affecté dans son infinité immanente par le fait qu’il y a cet en-plus qu’est le monde infini. Ce qui, logiquement, donne la conclusion suivante : si vous ajoutez du fini à l’infini, ça ne change rien. On peut éventuellement tourner ça en définition. C’est proche de la définition de Dedekind, mais c’est pas tout-à-fait la même chose.

Le plus simple, c’est d’ajouter le moins possible. Par exemple, d’ajouter 1. On pourra dire : est infini quelque chose telle que si on lui ajoute 1, elle reste pareille. Vous voyez que là aussi on touche à l’idée de succession. Dans la succession des nombres, quand vous ajoutez 1, c’est pas pareil, et c’est quantitativement pas pareil. 3, c’est réellement plus que 2. L’idée, ici, c’est que si c’est infini, et si vous ajoutez 1, c’est comme si vous ne faisiez rien. En effet, dans les infinités au sens de Cantor, si vous ajoutez 1 à l’infini, la cardinalité n’est pas modifiée.

Est-ce que, dans un topos, nous avons 1, et nous avons : ajouter quelque chose à ?

1, nous l’avons, c’est l’objet terminal. Et encore une fois, il y a des raisons sérieuses de penser que ce 1 est réellement 1. Sa façon d’agir, et sa capacité à pointer élémentairement quelque chose, le désigne bien comme 1.

Ajouter ? Nous avons une opération analogique, qui s’appelle la somme, et qui est le co-produit. On peut parler du co-produit, ou de la somme, par exemple de N et de 1. Dans tout topos, le co-produit de deux objets quelconques existe, en vertu d’une propriété de tout topos qui est que dans un topos, existent les limites et les co-limites de tout diagramme fini.

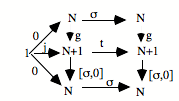
Supposons que nous soyons dans un topos où il y a un objet nombre naturel.[19] Alors, il y a la somme N+1 qui se présente de la façon suivante :

Ce diagramme est limite pour tout diagramme du même type :

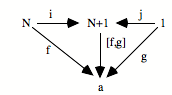
On peut dire que N+1 est en position de subsumption sur tout diagramme qui envoie des flèches de N et de 1 vers un objet quelconque. On trouve une subsumption et une unicité.

Revenons à notre situation initiale. Si nous avons un objet nombre naturel, nous avons certainement l’objet N+1 comme co-limite ou somme de N et de 1.

L’idée fondamentale va être la suivante. Ça va être de montrer que si N est un objet nombre, alors il est le même que N+1. C’est comme ça que nous allons passer à l’infinité intrinsèque. «Le même» en Catégories, c’est-à-dire N, va être isomorphe à N+1. Deux objets isomorphes sont identiques, à partir du moment où ils supportent le même type d’actions ; ils sont identiques, dès lors qu’ils sont structuralement, extrinsèquement, identiques. Il n’y a pas d’autre identité véritable, parce que les lettres, les objets, n’ont pas de caractérisation intrinsèque.

Notre programme serait le suivant : essayer de montrer que si N est un objet nombre naturel, alors N est isomorphe à N+1.

Nous aurons démontré quelque chose d’assez formidable, qui n’a pas d’exact équivalent ensembliste, qui est la chose suivante : s’il y a mauvais infini, il y a le bon. S’il y a le concept de la succession, il faut qu’en un certain sens, la lettre N nomme un infini, en un sens beaucoup plus interne, qui est son identité catégorielle à N+1. Et par conséquent, nous aurons démontré le fait que l’adjonction de quelque chose à N ne modifie pas fondamentalement N.

IV

Comment, dans cette présentation d’univers possible, le mot infini est-il exhibé ?

Il y a trois approches :

1) Infini comme indéfini, au sens spéculatif du mauvais infini. La répétition sans point d’arrêt. L’itération de la même opération produisant de l’autre. Un certain type de dialectique du même et de l’autre.

On peut se référer au Timée qui est une cosmologie présentée dans la fable de la création démiurgique. Les lois de l’univers y sont exhibées comme les lois de son façonnage. Il y a coextensivité entre le façonnage de l’univers et son intelligibilité. Au moment où le démiurge façonne l’âme du monde, il y a le geste crucial d’harmoniser le même et l’Autre (35b) : «par force avec le même la nature de l’Autre, nature rebelle au mélange». Violence (bia) est faite à l’Autre si on tente de le mixer au même. L’essence de l’altérité est rebelle à s’assortir à quoi que ce soit. La nature (fusi) de l’Autre n’est rien d’autre que l’altérité (comme l’explique le Sophiste ). Mais pour qu’il y ait univers, il faut que, de force, cette nature essentiellement fuyante de l’Autre, soit contrainte à cette harmonie.

On pourrait soutenir qu’il y a, dans l’infini, — en déplaçant le propos platonicien, le cosmos platonicien est fini — ceci que l’identification de l’altérité relève toujours d’un geste forcé. Il y a, dans l’idée de l’infini, l’assignation d’une perpétuelle violence qui s’apparenterait au geste du démiurge, à l’harmonisation forcée de l’Autre et du même. Quelque chose d’autre surgit dans le répété lui-même, harmonise le même et l’Autre sous le signe de l’indéfini. Il y a quelque chose d’essentiellement numérique dans la démiurgie platonicienne. L’Autre est fixé au même dans son altérité même. C’est, pour Platon, ce qui est au cœur de l’âme du monde. Un jeu forcé du même et de l’Autre par quoi tout univers peut se déployer.

2) L’infini comme propriété formelle de la multiplicité (cf. la définition de Dedekind).

3) L’infini comme champ opératoire.

Le cheminement dans lequel nous sommes engagés consiste à montrer que ces trois approches sont nouées dans le mode propre sur lequel se présente la question de l’infini dans un topos. Le topos va nous montrer que ces trois intelligibilités de l’infini ont entre elles une connexion que la pratique séparée de chacune d’elles ne permet pas d’établir. La logique sous-jacente à la décision fait apparaître des connexions invisibles de l’intérieur de cette décision.

Comment se présente le labeur de la chose ?

- On commence par capturer l’idée de succession, de l’opération qui va se répéter.

- On va montrer que, cette capture faite, on a nécessairement introduit un objet qui a une propriété intrinsèque.

- On va montrer que cet objet obéit aux principes opératoires disposés dans les axiomes de Peano.

On aura donc montré que les trois voies d’accès à l’infini, si on les logicise, sont connectées, se déduisent les unes des autres. C’est donc un processus de réunification des orientations de la pensée sur l’infini. En particulier, du point de vue de l’intelligibilité d’un univers quelconque, on peut ne pas avoir d’infini du tout, mais s’il y en a, il faut assumer les trois sens. Ce qui veut dire que l’opposition entre indéfini et infini ne tient pas. Il n’est pas vrai que l’un est la relève de l’autre, comme le dit Hegel.[20] En réalité, il n’y a qu’un et un seul concept de l’infini, dont les trois approches sont des facettes.

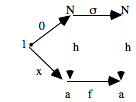
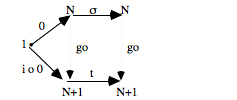
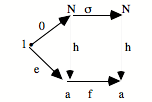
Une succession universelle doit pouvoir subsumer toute succession particulière.

S’il existe, dans un topos, un objet N, une flèche s de N vers N, et un élément 0, et que pour toute succession particulière f, il existe une et une seule flèche h qui fasse commuter tout le diagramme, on dira que [0, N, s] est en position universelle pour la succession.

On pourra dire que s, c’est la succession, le concept de succession dans le topos subsumant toute succession possible.

Il est requis que la flèche h soit unique (une position universelle combine la subsumption avec une position d’unicité).

[0, N, s] : Objet Nombre Naturel.

Il n’est pas requis qu’il y ait un objet nombre naturel dans un topos. La logique ne prescrit pas qu’il y ait de l’infini.

Nous avons montré :

1) que s est un monomorphisme : une flèche qui conserve les différences.

2) que sn ≠ sq, chaque fois que q < n.

Si l’on répète s n fois, on obtient une flèche différente de toutes les flèches obtenues en répétant toutes les flèches moins de n fois. Ce qui veut dire que nous produisons de l’autre. La répétition de s produit de l’autre.

Remarquons ceci :

s o 0 est un élément de N ;

s o s o 0 est aussi un élément de N. Mais le théorème précédent m’indique que c’est un élément différent, un autre élément de N. Et ainsi de suite. Intuitivement, cela signifie bien qu’il y a une infinité d’éléments de N. Mais infinité ne veut rien dire ici. Très précisément : étant donné un élément de N, de la forme sn o 0, je peux toujours en produire un autre, en refaisant s.

Nous sommes au point où ce dont il s’agit c’est que l’application du même, je suis sûr que ça me donne de l’autre, un autre élément de N.

Venons-en à l’infinité intrinsèque. Nous allons partir d’une variante de la propriété de Dedekind : un ensemble est infini si en lui ajoutant 1, on ne change rien ; on ne modifie pas son être quantitatif. L’infini, c’est ici la nullité du plus-un.

Il va falloir utiliser le concept d’adjonction ou de somme tel qu’il existe dans un topos : le co-produit de deux objets (p.27).

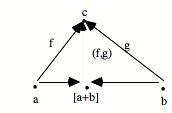
[f,g] est en position universelle, le concept même de être visé depuis a et depuis b. C’est la synthèse de ce qui peut venir simultanément de a et de b. Le lieu synthétique des actions qui procèdent à la fois de a et de b.

Ex : dans le topos des ensembles, [a+b] c’est ab.

Notre but va être de montrer que N et N+1 sont le même, c’est-à-dire que N et N+1 sont isomorphes, structuralement indiscernables. Dans un topos, [N+1] existe nécessairement en tant que produit.

A)

B)

t = i o [s,0]

puisqu’elle est de [N+1] vers [N+1], je peux la prendre comme flèche itérative.

[s,0] o j = 0 (A)

[s,0] o t = [s,0] o i o [s,0]

[s,0] o i = s

[s,0] o t = s o [s,0]

Donc, tout le diagramme du bas commute. La flèche de N vers N fait commuter tout le diagramme. Donc, c’est forcément la même qu’IdN, en raison de l’unicité, puisque IdN fait aussi commuter le diagramme.

[s,0] o g = IdN

Stratégie très courante en théorie des catégories : deux diagrammes dont il s’agit d’établir qu’ils commutent, d’où se déduit l’identité des flèches.

(1)	t o i = i o [s,0] o i t o i = i o s Donc, (1) commute.

(2)	g o s o 0 = t o g o 0 = i o [s,0] o g o 0 = i o IdN o 0 = i o 0 Le triangle commute. Qu’en est-il du carré ? g o s = t o g g o s o s = t o g o s Donc, le carré commute. Mais il ne doit y avoir qu’une seule flèche qui fait commuter. Donc : g o s = i

(3)

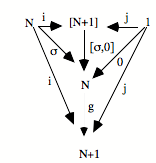
Le triangle (N,N,N+1) commute, à raison de ce que g o s = i.

Mais, d’après (B), g o 0 = j.

Donc, le triangle de droite commute.

Donc : g o [s,0] = IdN+1 en raison de la flèche qui fait commuter le triangle.

Or : [s,0] o g = IdN

Donc :

Remarques sur la démonstration catégorielle

I) - La démonstration catégorielle, bien qu’on puisse la démontrer de façon algébrique, est tout de même plus immédiatement prise dans l’évidence diagrammatique. Donc, il faut visualiser la situation. Il faut construire les flèches qui correspondent à la situation.

 - On est toujours renvoyé au diagramme de définition. Il faut tenter de faire surgir, de l’intérieur de cette situation connue, les flèches dont on a besoin.

 - Il faut utiliser à fond les propriétés d’unicité. La contrainte d’unicité donne des égalités.

II) Pour une bonne part, la démonstration consiste à présenter dans des positions diagrammatiques différentes, et sous des noms différents, des flèches qui, en réalité, sont identiques. Il faut s’habituer au caractère constamment déplaçable de l’égalité. A partir de là, on montre cette identité en utilisant des propriétés structurales. Le ressort est de disposer des actions identiques dans des réseaux différents, c’est-à-dire dont les systèmes de contraintes sont différents.

Dans notre démonstration, nous avons testé des identités dans un réseau de type co-produit, et dans un réseau de type nombre naturel. Donc, on essaie d’atteindre des identités élémentaires, de flèches, en utilisant des différences qui sont des différences de situation. On peut appeler ça une épreuve géométrique de l’identité. C’est un grand classique de la géométrie : étudier ce qui est invariant dans des changements de situation. C’est en ce sens-là qu’on peut dire que l’esprit général de la théorie des topos est géométrique.

A un niveau plus déployé, ça va intervenir avec la logique proprement dite. Ça va aboutir à l’idée que certaines vérités peuvent être liées à certaines situations, être faiblement invariantes par rapport à des transformations de situations générales. Ceci amènera à une doctrine des vérités locales. Nous allons avoir une géométrisation de la vérité, par variation locale des flèches, y compris des flèches logiques.

Nos résultats sont les suivants :

0) définition de {N, 0, s} dans un topos,

1) sn ≠ sq

2) N N+1

Notre troisième tâche est de considérer comment les choses se présentent quand on les aborde d’un point de vue opératoire. Comment les axiomes de Peano singularisent-ils l’opérateur de succession ?

Il y a trois propriétés :

• —⁄

0 est réellement un point de départ. C’est l’axiome du point de départ. Il n’y a pas non plus de boucle qui revienne sur 0.

• Deux entités qui ont le même successeur sont identiques :

—⁄

La succession est linéaire, ni circulaire, ni arborescente.

• Induction complète :

Si 0 a une propriété, et si à chaque fois qu’une entité a une propriété, son successeur l’a aussi, alors toutes les entités ont la propriété :

—⁄

—⁄

Mais ceci n’est pas comme tel démontrable.

Appelons w l’ensemble supposé des entités concernées ( w [champ opératoire de s] ),

A w, un sous-ensemble de w

—⁄

—⁄

L’axiome de l’induction complète a été considéré par certains mathématiciens comme le cœur des mathématiques : la capacité à tirer, de prémisses opératoires, des propriétés universelles. Il y a des commentaires approfondis de Poincaré là-dessus. Pourquoi cela lui paraît-il si central ? Parce que c’est une postulation qui fait un saut dans la pensée. Poincaré voyait là à la fois l’essence et la limite de la pensée mathématique. Il y a un outrepassement de l’opératoire. En réalité, on suppose un tout en passant au pour-tout, alors que le successif n’inclut pas de tout. C’est là qu’on bascule de l’indéfini à l’infini. Ce que Poincaré disait, c’est que les seules suppositions d’infinité possibles sont celles qui dérivent de l’opératoire.

Notre question, à partir de là, est : est-ce que ces axiomes peuvent prendre sens avec notre objet nombre naturel, dans un topos ?

Pour les deux premières propriétés, c’est immédiat :

- sq o 0 ≠ 0

- sn ≠ sq n ≠ q.

Le problème, c’est le troisième axiome. Il faut d’abord lui donner sens.

• Il va falloir nous donner un concept quelconque de l’inclusion : A N.

Nous savons qu’un sous-ensemble de N est transcrit catégoriquement sous la notion de sous-objet de N[21] :

• Il va falloir que nous donnions sens à l’appartenance, et à l’appartenance à un monomorphisme. A l’idée de l’appartenance d’une flèche élémentaire à une autre flèche.

Sous ces conditions, il faudra que nous démontrions que notre sous-objet est identique à l’objet. Il va falloir montrer que le monomorphisme m est élémentairement équivalent à Id(N).

Les étapes seront les suivantes :

- Travail définitionnel : • un sous-objet,

• l’appartenance d’un élément à une flèche quelconque.

- Travail de transcription : de l’axiome de l’induction complète en termes catégoriels.

- Travail de démonstration, c’est-à-dire de désaxiomatisation : la conclusion pour-tout x, une fois qu’on a les prémisses, elle est vraie. Nous allons donc transformer les axiomes de Peano en pures et simples propriétés de l’objet N.

V

a) Forme de la répétition avec point de départ, et sans point d’arrêt ni boucle : - «Encore un» - Même / Autre b) Forme intrinsèque. Il existe des parties aussi grandes que le tout. - Le plus-un est nul. c) Propriétés opératoires axiomes de Peano

a) (position limite, ou universelle) Tous les sont différents. b) c) (N, s, 0) valide les axiomes de Peano. s est un monomorphisme Il existe une flèche élémentaire e telle que :

Comment exprimer en langage toposique le concept ensembliste  ?

Nous avons le concept de sous-objet : monomorphisme de cible N, qui est une différenciation stable de l’objet. Un sous-ensemble est l’inscription stable d’une différence ; fonction caractéristique à deux valeurs possibles : y être ou n’y être pas.[22]

Il existe une flèche élémentaire e telle que : m o e = 0

Dans un topos, il y a l’idée d’élément, comme toujours, sous forme de flèche.

S’il existe un élément de ce qui va saisir 0, nous serons autorisés à penser que 0 est en position d’appartenance au monomorphisme.

L’idée est que nous avons la situation suivante :

Si le triangle commute, m o e = 0

Définition générale : si nous avons k o x = g, nous disons que g Î k (k, flèche quelconque, x, flèche élémentaire).

Ici, 0 est sous une dépendance élémentaire de m. Le 0 est saisi par m du biais d’une composition élémentaire.[23]

Partons de l’intuition ensembliste. Le fait que, si on applique s à quelque chose qui est dans A, on trouve quelque chose qui est dans A, signifie que l’opérateur s, quand on démarre dans A, ne fait jamais sortir de A. Il faut trouver une transposition de ça.

L’idée est que si on enchaîne s sur m, on va rester dans m : s o m Õ m. Reste à spécifier la relation : Õ. C’est la relation d’inégalité entre sous-objets (p.101-103 du fascicule).

Etant donnés des monomorphismes d’un objet quelconque, on dira que : f Õ g s’il existe h tel que g o h = f.

Notons que peuvent exister deux sous-objets non comparables : il n’existe pas, dans l’univers considéré, de flèche h qui fasse commuter le triangle. La relation d’ordre n’existe pas toujours dans l’univers entre tous les objets. Elle peut être une relation d’ordre partiel.

Appliquons la définition que nous venons de donner à : s o m Õ m.

Cela veut dire qu’il existe g telle que : m o g = s o m.

Nous serons fondés à dire que, appliquée à m, s ne fait pas sortir de m, nous laisse dans l’immanence, s’il existe une flèche g telle que : m o g = s o m.

S’il existe un diagramme commutatif tel que celui-ci, nous avons bien : s o m Õ m

(Ceci achève nos hypothèses de l’induction complète).

Comment va s’exprimer le saut : A = w, en langage toposique ?

m ª Id(N) [ª : équivalent][24]

De quoi s’agit-il ? Si nous arrivons à démontrer qu’un monomorphisme de cible N, un sous-objet de N, qui valide les conditions que nous venons de voir, est en réalité équivalent à Id(N), nous aurons en réalité montré que N valide les axiomes de Peano, y compris l’induction complète.

Si nous avons nos conditions, alors, dans un univers toposique, c’est vrai le pour tous. Le pour tous signifie ici l’Id(N). A la différence de l’ensemblisme qui parle de multiplicités, ici ça parle d’identité. C’est donc le passage d’une totalisation à une identification. Le premier mouvement est un mouvement de désobjectivation, le second de détotalisation. Ce sont des caractéristiques de l’installation de la pensée dans la logique qui est toujours au prix — ou au bénéfice — d’une désobjectivation, d’une minimalisation maximale de l’objet qui le ramène à la lettre. L’imminimalisable de l’objet, c’est la lettre, dirait-on en reprenant Beckett dans Cap au pire  ! Mais cette exténuation de l’objet, c’est aussi l’absolu primat de la relation, c’est-à-dire de la flèche. Ce mouvement en véhicule un autre qui est qu’on va détotaliser maximalement jusqu’à n’avoir que des relations d’identités.

Ce qui veut dire aussi qu’en sens inverse, toute décision ontologique, c’est de l’institution d’objets. C’est toujours poser qu’il y a autre chose que la lettre. Il y a un point d’irréductibilité littérale. Et puis, c’est toujours aussi retotaliser : la totalité concrète, dirait Althusser.

Mais, dans ce va-et-vient entre logique et ontologie, il y a toujours une trace de l’un dans l’autre. Toute installation dans la logique est toujours sous l’horizon d’une décision ontologique, et inversement. Le marquage dans la logique de la décision ontologique répudiée, c’est que l’identité est fuyante, comme si elle portait avec elle l’ombre de la totalité répudiée.

Quand on veut détacher l’identité du pluriel, du collectif, on y parvient, mais l’identité est fuyante. Elle est intérieurement marquée d’une pluralité évanouie.

Je pense que ça a une grande signification politique, surtout aujourd’hui où les questions du débat entre identité et totalité sont centrales. C’est le grand débat sur communautarisme, ethnie... Une communauté se représente-t-elle comme totalité ? Il y a des raisons de dire que la voie dé-totalitaire, identitaire, est la voie progressiste. Mais il ne faut pas perdre de vue que cette voie est logicisante, et qu’elle est à un moment donné sommée de dire quelle est sa décision ontologique sous-jacente.

La voie de l’identification détotalisante, qui est la voie de l’universalité, ne doit pas non plus s’imaginer qu’elle a d’elle-même absenté toute trace de la totalité, parce que ce n’est jamais exactement vrai. Toute voie identitaire traite non pas une absence de totalité, mais des débris de totalité. Il n’y a pas d’installation logique pure, et il y a un moment où l’identification bute sur sa propre fuite.

Dans toute pensée, il y a deux choix. Il n’y a pas de ligne pure de la pensée. Mais toujours deux registres. Aussi loin qu’on pousse une orientation, on est obligé à un moment donné de reconvoquer l’autre.[25]

Démonstration

Nos conditions sont les suivantes :

I- m o e = 0 0 Î m

II - s o m Õ m

Nous allons considérer le diagramme suivant (III) :

Par définition, le diagramme du haut commute.

Je vais démontrer que celui du bas commute :

Donc, le diagramme du bas commute.

Donc, tout le diagramme commute.

Donc, il y a une flèche unique qui doit le faire communter.

Donc, m o h = Id(N).

Cela signifie que : Id(N) Õ m

Mais il est clair que : m Õ Id(N)[26]

Ce qui signifie que : Id(N) = m

Nous avons démontré que, si nous avons I et II, alors nous avons III, et Id(N) = m.

Ce qui est le schéma de l’induction complète.

Le système (N, s, 0) vérifie les axiomes de Peano.

Finalement, qu’avons-nous fait ? Nous avons montré que, dans un espace logique, où il y a un concept de la répétition, ou de l’indéfini, ou du mauvais infini, ou du encore un ..., alors il y a aussi le fait que N est isomorphe à N+1. Donc le +1 est nul. Et il y a aussi que les axiomes de Peano sont valables. Cette fois, la conclusion est déduite.

L’universalité de la question de la succession, d’une part contraint à ce qu’il y ait la nullité du +1, et d’autre part contraint les axiomes de Peano comme figure opératoire.

On peut donc, à ce stade, dire qu’il y a bien une unité du concept d’infini. Cette unité est donnée comme une limite, celle du diagramme de succession. Mais la question qui demeure est : y a-t-il sens ou non à parler d’une pluralité des infinis ?

Pour Cantor, sa trouvaille portait plus sur la pluralité de l’infini — opération de dissémination de l’infini, dessoudé de l’un — que dans le concept d’infini proposé, unificateur et actuel. Entre l’infini et l’un, il n’y a aucun accord intrinsèque.

On pourra appeler infini quelquechose qui a la stucture de N, qui noue les trois dimensions : répétitive, intrinsèque, et opératoire.

La question de la pluralité des infinis concerne la question de savoir comment on pourrait représenter, dans un topos, l’idée du continu.

Le deuxième grand problème que nous allons traiter la prochaine fois, c’est la catégorie de différence.

- Topos bien pointé (78-79) ;

- Retour sur le problème de l’Objet Central (14-40).

Notre objectif va être la démonstration du théorème : un topos est bien pointé si, et seulement si, il y a unicité du vide et logique classique. Admirable théorème ontico-logique !

Le problème de savoir s’il existe ou pas des différences globales traverse, comme une pré-option décisive, l’histoire de la philosophie, parce que ça engage une doctrine de l’intuition.

Le traitement toposique fait apparaître que si on veut faire l’économie de quelquechose qui touche à la vie comme catégorie de la pensée, des différences globales, l’installation dans l’univers logique va obliger à assumer :

- qu’il n’y a qu’un vide,

- que la logique est classique.

Sinon, il faut admettre plusieurs vides, ou que la logique n’est pas classique : rejeter le principe du tiers exclu, de l’équivalence de l’affirmation et de la double négation.

VI

Nous allons nous engager sur la question de la différence.

Comment se construit le concept même de différence de l’intérieur d’un topos ?

Quelques rappels.

• On peut considérer que l’assertion il y a de la différence est au point de départ de toute philosophie. Ce n’est pas un concept régional ou singulier. Rendre raison de ceci qu’il y a de la différence est une question primordiale. Le poème de Parménide — qui peut être considéré comme le poème du même, de l’un — commence par une affirmation de différence : il y a deux voies.

Ceci est un point universel. Il y a philosophie sous condition qu’il puisse y avoir l’assertion du différenciant comme telle.

• Le il y a de la différence est modulé selon les philosophies. Il y a un mouvement premier de localisation de la différence qui va fixer la nature singulière de la trajectoire.

Donc le problème de la différence est toujours double. Il est le il y a de la différence qui est si originaire qu’il n’est que la supposition d’un il y a . Et le deuxième versant de la question est le problème de la localisation.

Il faut se reporter au début du Parménide de Platon. La théorie des Idées n’est rien d’autre qu’un protocole de résolution de la question de la différence. Les Idées, c’est le fondement du différenciant. Les Idées, ça doit rendre compte aussi de ce que la boue et les cheveux, c’est pas la même chose. Le point ici souligné par Parménide c’est que, aussi, la question est de savoir quel espace de localisation on assigne à cette question de la différence.

Cette question de la différence est toujours croisée par celle du local et du global. Il y a nécessairement aussi une topologie de la différence.

Cette question du croisement de la question de la différence dans son versant identité/différence, et de la topologie, est une question qui a toujours une grande portée, dans tous les ordres de la pensée : notamment en politique. Dans le marxisme classique, le concept de classe est un différenciant global. Mais la question est toujours de savoir quelle est la localisation de cette globalité. La classe n’est jamais là. D’où des concepts subordonnés comme : position de classe ou point de vue de classe : au regard d’un espace de déploiement effectif, il y a une disposition subjective, localisable.

Il y a des opérateurs de localisation : soit objectif, soit subjectif, assignant en un point le principe du différenciant global. Chez Mao-Tsé-toung, les masses désigne la différence entre la substance d’ensemble du phénomène politique et une résistance qui existe sous une autre forme que le concept de masse. D’où la spécification nécessaire de situation de masse, et une doctrine de la localisation singulière : l’exemple-type, concept médiateur entre la localisation de la différence et son signifiant global, les masses.

Le gros problème, de ce point de vue-là, a toujours été l’État qui est typiquement un différenciant global, et donc renvoyé au différenciant primitif : État de classe ... D’où la question nouvelle : qu’est-ce qu’une localisation de l’État ? Où l’État atteste-t-il la différence avec ce qui n’est pas lui ? Quel est, en termes d’État, le rapport entre le local et le global ? C’est une question complexe qui ne se résout pas en termes ensemblistes, par «morceaux» (un groupe de policiers, le Président de la République...). Toute la difficulté, et la vacillation, du concept de révolution porte sur l’idée que l’État ne peut être traité que globalement. La thèse révolutionnaire est : il n’y a de l’État qu’un traitement global. Or l’expérience a montré qu’en maintenant l’État dans son principe de différenciation globale, on ne fait que le re-produire, en perpétuer la nature.

De même, la question de la différence des sexes. S’agit-il d’une différence globale ou localisable ?

Nous, nous proposons d’examiner la question de la différence dans la tension du global et du local.

Nous sommes en logique, donc au régime du possible. Il faut bien s’attendre à ce que des considérations sur une différence nous entraînent sur des conséquences qui touchent au local et au global.

Deux flèches sont différentes si elles n’ont pas même cible et même source. Donc la question de la différence de deux flèches ne va se poser que si nous avons même source et même cible :

différenciation “objective” par les objets, littérale

atome de la différence

Le vrai principe du réel, dans la théorie des catégories, c’est les flèches. Si on en reste là, on ne sait pas que f et g sont différentes. On peut déclarer qu’elles ne le sont pas. J’entérine en logique qu’il y a de la différece, c’est-à-dire qu’il y a possiblement de la différence. Mais le il y a de la différence supposée ne me dit rien sur la différence elle-même. Il n’y a pas de critère de la différence autre que d’avoir supposé qu’elle peut être. L’élaboration va consister à remplir point à point ce il y a de la différence purement logique par un certain nombre de déterminations, qui vont être des différenciations de la différence.

Ces différenciant sont nécessairement externes. Il n’y a rien à l’intérieur des flèches qui me permette de dire : voilà ce qui les différencie. L’espace logique, un topos, est fondamentalement un espace de l’extériorité. Parce que je ne me donne aucune intériorité. Il faudrait une décision ontologique. En théorie des ensembles, je me donne le signe de l’appartenance. Dans la logique, je n’ai que des déterminations externes. Je vais différencier les flèches dans des réseaux de corrélations.

Donc :

• j’assume la possibilité de la différence,

• cette différence n’a aucune attestation immanente,

• pour l’élucider un tout petit peu, il va me falloir faire intervenir des déterminations externes. La différence ne va pouvoir être spécifiée que si je l’encadre. Une différence n’est pensable que contextuellement. Mais le contexte, c’est déjà une certaine réquisition du global. C’est la catégorie. En termes catégoriels, si la différence était isolée, je ne pourrais pas aller au-delà de l’assertion de possibilité de cette différence.

Il y a un cas où on sait que f et g sont forcément différentes : si elles succèdent à une seule action et si le résultat est différent :

f o h ≠ g o h Þ f ≠ g

Si je constate ça, c’est sûr que f et g sont différentes.

Je donne là une «condition relative» de la différence. L’évaluation de la différence est renvoyée contextuellement à l’évaluation d’autres différences, dans un espace élargi. De contexte en contexte, on est effectivement renvoyé au global, et en particulier à la question : est-ce qu’il y a une différence ?

Un des points-clé de la notion de topos, c’est que, dans un topos, s’il n’est pas réduit à un point, il y a une différence sûre, au moins : celle entre 0 et 1 ; et donc la différence entre le vrai et le faux :

Au fond, 0 et 1 garantissent qu’il y a de la différence entre flèches, sous réserve qu’eux-mêmes soient différents. On peut au moins dire : s’il y a deux objets différents, alors il doit aussi y avoir un atome de différence réelle. L’opération contextuelle n’est pas dépourvue de sens.

Une fois ceci établi, on va se livrer à des opérations conditionnelles contextuelles :

C’est le minimum atomique d’affection de a ; si f o e ≠ g o e Þ f ≠ g.

Nous avons là le diagramme atomique d’une localisation de la différence. f et g diffèrent en un point. f et g sont élémentairement différentes. Et on dira que la différece entre f et g est localisée (en un point). De la différence locale s’ensuit la différence globale. Alors que de l’identité locale, on ne peut conclure à l’identité globale. Donc, c’est très important d’avoir cette situation : f o e ≠ g o e, parce qu’il n’y a pas besoin de voir ailleurs.

De là, on peut se dire : ce ne serait pas mal d’avoir un univers où ce serait toujours le cas : un univers qui obéirait partout à la règle où, chaque fois qu’on a deux flèches parallèles, il existe un élément qui les différencie élémentairement.

Si f ≠ g Æ ($e) [ f o e ≠ g o e ]

Dans ce genre de situation, on peut toujours trouver un point où la différence se joue. Une différence globale, dans un tel univers, a toujours une attestation élémentaire, ou locale.

Quand c’est le cas, on dit que le topos est bien pointé. Un topos bien pointé est un topos où, sur la question de la différence, on a une articulation universelle entre le global et le local.

La propriété d’être bien pointé est une propriété bien particulière, et une propriété forte. C’est une propriété différenciante de la différence tout-à-fait particulière. Un exemple flagrant de topos bien pointé, c’est les ensembles.

Une question fondamentale, dans un espace de pensée quelconque, c’est de savoir si l’univers de référence est bien pointé ou pas.

Quelles sont les conséquences de l’hypothèse que le topos est bien pointé, ou n’est pas bien pointé ? (cf p. 78-79 du fascicule)

• La première grande caractéristique d’un topos bien pointé, c’est qu’il y a unicité du vide. C’est la caractéristique ontologique fondamentale. (cf p.79-80)

Nous nous situons dans un topos bien pointé.

Nous supposons l’existence d’un objet vide, non isomorphe à 0. (S’il y a une flèche de 1 vers 0, le topos est dégénéré).

Ces deux flèches sont différentes. Nous sommes dans un topos bien pointé. Donc, elles doivent être élémentairement différentes. Donc, il faut qu’il y ait un élément de a :

Conclusion : si un objet est vide, il est isomorphe à 0. Dans un topos bien pointé, il n’y a pas d’autre objet sans élément que O. A un isomorphisme près.

Donc, nous avons l’inférence suivante, démonstrative : si toute différence existe en un point, alors il n’y a qu’un seul vide, qu’un seul objet sans élément. Ce qui veut dire que, lorsque deux objets sont différents, il y en a au moins un qui n’est pas vide. Donc, la différence entre deux objets implique au moins l’existence d’éléments.[27]

• Conséquence logique

Nous allons montrer que : topos bien pointé Æ - deux valeurs de vérité

- l’objet central n’a que deux éléments : le vrai et le faux ; la logique est bivalente.

Il y a une corrélation entre la question de la différence, et la question du deux.

En substance, une valeur de vérité, dans un topos, est un élément de l’objet central. Il n’y a aucune raison de supposer, à partir du topos, que l’objet central n’a que deux objets. Ces éléments se disposeront entre le vrai et le faux, avec une infinité de valeurs intermédiaires.

Le choix de vérité, ou le choix de valeur, est binaire : c’est ça, ou c’est ça. Ce qui rapproche cette logique d’une logique de la décision. Le bien pointé est du côté du décisionnel. Tandis que le pas du tout bien pointé est plutôt du côté de la logique de l’intuition.

Nous savons que, dans un topos, existe toujours ce pull-back. Tout élément de C est la centration d’un sous-objet de 1. Et inversement. Nous avons une corres-pondance stricte entre éléments de l’objet central et sous-objets de 1.

Pour étudier les valeurs de vérité dans un topos, on peut tout aussi bien étudier les sous-objets de 1. La logique, à son niveau élémentaire, c’est-à-dire les valeurs de vérité, s’est projetée dans la question des sous-objets de 1. On a une corrélation entre les structures logiques de la pensée, et la question de l’Un, et même de la structure de l’Un (cf les neuf hypothèses du Parménide de Platon).

Ce que l’étude toposique met en évidence, c’est qu’en effet la question des valeurs de vérité, on peut tout-à-fait l’envisager comme la question du marquage des sous-objets de Un. La question de la logique, c’est au fond la question : de quelle(s) différence(s) l’Un est-il capable ? Les univers logiques possibles, les inflexions de la logique, vont dépendre entièrement des inflexions différenciantes de l’Un.

Il est très frappant de voir comment Platon a eu une intuition de cela. Jusqu’à quel point l’Un se laisse-t-il différencier par l’Autre ? C’est la clef ontologique de la logique. Si l’Un ne se laisse affecter d’aucune manière par l’Autre, alors il n’y a aucune logique. Nous pouvons donc remplacer la question : combien de valeurs de vérité ?, par la question : combien de sous-objets de 1 ?

Nous savons que, dans un topos non dégénéré, existent :

Þ

Supposons qu’il y en ait un troisième.

Il faut qu’il y ait un troisième sous-objet de Un :

a ne doit pas être isomorphe à 0, et a ne doit pas être isomorphe à 1.

Ce qui apparaît, c’est que m est nécessairement un épimorphisme aussi.

Si a ≠ 0, a n’est pas vide :

Supposons que : f o m = g o m

f o m o e = g o m o e

f o Id(1) = g o Id(1)

f = g

Or, c’est un monomorphisme. Donc, c’est un isomorphisme.

Par conséquent, dans un topos bien pointé, nous échouons à introduire une troisème valeur de vérité. Donc, dans un topos bien pointé, il n’y a que deux valeurs de vérité, le vrai et le faux. Nous sommes dans une logique de la décision, bivalente, de façon aussi contrainte que nous avions unicité du vide.

Si la différence est localisable,

1) il y a unicité du vide,

2) il n’y a que deux valeurs de vérité.

Deux valeurs de vérité, c’est assez proche de ce qu’on connaît d’habitude dans les logiques classiques. Donc le fait qu’il n’y ait qu’un seul vide, et que la logique soit classique (bivalente), est-ce que ça ne veut pas dire que la différence est localisable ?

Pour voir si la réciproque est vraie, il va falloir stabiliser le concept de logique classique. Bivalente ne va pas suffire ; ce qui compte dans cette logique de la décision, c’est l’autorité du deux. Ce qui ne veut pas dire qu’il n’y a que deux choses. Si on convient d’appeler classique une logique qui entérine l’autorité du deux, il faut trouver une définition plus forte que : elle reconnaît deux valeurs de vérité.

Notre cheminement va être le suivant :

1) Tenter de donner une définition de ce que c’est, dans un topos, que l’autorité du deux. Définir la logique classique dans un topos.

2) Ensuite, nous demander si on combine logique classique et unicité du vide, qu’est-ce qui se passe ? Nous verrons qu’on a bien pointé. C’est un très beau théorème.

Sur l’autorité du deux  :

Dans un topos, on a 1, et encore 1 : le co-produit.

Cela, ça existe toujours. On dira qu’un topos est classique quand la flèche somme [V,F] est un isomorphisme. Cela ne veut pas dire que l’objet central n’a que deux éléments. Dans tous les cas, cette flèche, c’est un monomorphisme (très compliqué à démontrer) . Donc, il faut montrer que c’est un épimorphisme.

VII

Sur la différence

La question est celle de la corrélation entre l’ontologie de la diffiérence et la nature intime de la logique. La grande cible de tout ça est le théorème selon lequel il y a équivalence entre le fait qu’un topos soit bien pointé, et le fait que : • le vide soit unique,

• sa logique soit classique.

Un topos est bien pointé si, et seulement si, il a conjointement les deux propriétés d’unicité du vide et de classissisme de la logique.

D’un point de vue interprétatif, un topos bien pointé est un topos où toute différence est localisable, où il n’y a pas de différence qui soit purement globale. Le paradigme du topos c’est les ensembles.

Cette propriété ontologique de la différence, pour tout univers bien pointé, est équivalente à l’addition des deux propriétés : l’unicité du vide et le caractère classique de la logique. Si l’on assume que le vide est unique et que la logique est classique, on prend position sur la différence en général.

C’est un énoncé logico-ontologique. C’est cela que nous essayons de démontrer et de penser.

Le point est d’identifier ce qu’on appelle logique classique.

On serait tenté de dire qu’une logique est classique quand elle est bivalente. Ce qui semblerait dire qu’on a le tiers exclu. L’analyse toposique montre que la logique peut être classique même s’il y a plus de deux valeurs de vérité et qu’inversement, la logique peut ne pas être classique même s’il n’y a que deux valeurs de vérité.

C’est la question de : où s’établit la souveraineté du deux. On admettra qu’une logique classique est une logique qui établit une certaine souveraineté du deux parce que c’est une logique de la décision — c’est sans doute sa caractéristique la plus profonde —. On ne peut pas s’égarer dans un labyrinthe d’options. Le deux étant ici la matrice du choix, mais cela ne veut pas dire qu’il n’y a que deux valeurs de vérité. Parce que cela, c’est une interprétation extensionnelle et statique, ensembliste dans le mauvais sens.

Mais la question est la puissance structurante du deux quand il n’y a pas deux mais beaucoup plus. La vraie question est de savoir comment il peut y avoir une souveraineté du deux même sur une infinité de valeurs de vérité. Le point crucial c’est qu’a contrario, le fait qu’il y ait du deux ne garantit pas la souveraineté du deux.

Remarque  : Il y a deux valeurs de vérité, c’est pas quelque chose qui a sens de l’intérieur d’un topos, parce que c’est ensembliste, parce qu’on compte aussitôt comme un ensemble les éléments de l’objet central.

La souveraineté du 2 va concerner la structure de l’objet central, et non pas le nombre de ses éléments. Mettre le 2 au centre, non pas comme nombre, mais comme opération centrale. 2 doit être ici pris purement comme un et un. Comme la juridiction c’est l’objet central, ce qu’on va avoir, en gros, c’est une isomorphie entre l’objet central et le 2, ce qui est tout autre chose que l’idée que le 2 a 2 éléments.

Comment figurer ce 2 ? Par 1 et 1 au sens catégoriel, c’est-à-dire du co-produit de 1 et de 1 :

Ceci est la co-limite du diagramme constitué par 1 et 1.

Ce 1+1 existe dans tout topos, puisqu’y existent toutes les co-limites finies.

L’idée va être que ce 1+1, par l’occurrence du vrai et du faux, va pouvoir être en isomorphie avec l’objet central quand la logique est classique.

Nous savons que, dans tout topos, il y a au moins deux éléments différents de l’objet central qui sont le vrai et le faux.

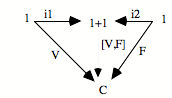
Ce diagramme existe dans tout topos. La flèche [V,F] existe dans tout topos.

On dira que la logique est classique si la flèche [V,F] est un isomorphisme.

Telle est la définition catégorielle du classissisme de la logique. Ça place donc la structure de l’objet central sous la juridiction du 2 par l’isomorphie de l’objet central et de 1+1. Même, on peut dire, en un certain sens, que l’objet central est le 2.[28]

Il n’y a aucune raison pour que [V,F] soit, en toutes circonstances, un isomorphisme. Ce n’est pas une propriété générale des topos. Sinon, on ne parlerait pas de logique classique.

1) Par contre, on démontre que : [V,F], dans tout topos, est un monomorphisme.

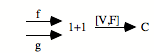[ [V,F] o f = [V,F] o g ] Æ f = g

Donc, cette flèche est un conservateur de différences. Quand on va vers l’objet central, le 2 structural conserve les différences. C’est ce qu’on pourrait appeler un certain pouvoir filtrant du 2. Donc on peut dire que le 2 conserve les différences en aval de lui-même.

Cela ne veut pas dire qu’est différent ce qu’on compte pour 2. Le co-produit fait du 2 avec lui-même. C’est du 2 structural pur. On fait du 2 sans discernabilité préalable.

Dans sa corrélation logique (à l’objet central), le 2 conserve les différences. Il n’est pas vrai que toute différence soit faite du 2 — parce que la différence peut se penser dans l’indiscernable —, mais il est vrai que le 2 conserve toute différence quant à sa signification logique. Il y a quelque chose du deux qui, logiquement, conserve la différence. C’est vrai dans tout topos.

Ce qui est remarquable, c’est que la démonstration de ce point est très compliquée. Pourquoi ? Il y a des raisons à cela : la raison que cette question du rapport du 2 et de la différence est, pour la pensée, une question complexe.[29]

2) Si l’on veut démontrer, dans tout topos, que la flèche [V,F] est un isomorphisme, il suffira de montrer que c’est un épimorphisme. Finalement, un topos est classique si [V,F] est un épimorphisme.

Nous allons démontrer qu’un topos bien pointé est toujours classique.

Soit un topos bien pointé :

Je veux démontrer : f o [V,F] = g o [V,F] Æ f = g f o V = f o [V,F] o i1 = g o [V,F] o i1 = g o V et f o F = g o F

Si f et g étaient différentes, comme le topos est bien pointé, il devrait exister e qui teste cette différence. Dans un topos bien pointé, toute différence a une assignation élémentaire.

Or ni V, ni F, ne discriminent f et g, nous venons de le démontrer.

Donc f et g sont égales, puisqu’aucun élément ne peut discriminer f et g.

Le résultat de cette démonstration est le suivant : la logique d’un topos bien pointé est classique. Dans un topos bien pointé, il y a souveraineté du 2, au sens où on peut dire que 1+1 est l’objet central. Donc, l’objet central est le 2.

Ce qui structure l’univers comme une logique de la décision, c’est que le 2 y est central : le 2 de la non-différence, le 2 du même.

Si un topos est bien pointé : le 2 est l’objet central. Cela veut dire que si la différence est localisable, c’est qu’au centre il y a le 2 qui n’est pas, lui, le 2 de la différence. Il n’a pas besoin de la différence pour se faire 2. Nous en avons un exemple bien connu : c’est le topos des ensembles.[30]

Pour marquer en réel cette différence entre la différence et le 2, je voudrais vous donner l’exemple d’un topos qui est bivalent, et qui cependant n’est pas classique. Entre le 2 saisi comme pure extension, et la souveraineté du 2 qui régit le classissisme logique, il n’y a pas identité.

Ce topos, généralement connu comme le topos M2 — action monoïdale M2 — va avoir les propriétés suivantes :

1) Il est bivalent ; il y a deux valeurs de vérité, le vrai et le faux ;

2) Il est non-classique (1+1 ≠ C) ;

3) Il s’ensuit nécessairement qu’il n’est pas bien pointé (il existe des différences globales) ;

4) Néanmoins, il y a unicité du vide[31] ;

5) Il valide le tiers-exclu[32] ;

6) La double négation n’est pas égale à l’identité : ¬ o ¬ ≠ Id[33]. Ce qui veut dire que ¬ o ¬, nétant pas l’identité, est un opérateur topologique. Cet objet est très intéressant.

Deux mots sur la présentation de ce topos :

On part de ceci : on part des ensembles, plus une structure dessus :

l [l(x)] = l(x) = x’

C’est une fonction qui, au deuxième coup, ne bouge plus. Une action qui ne marche qu’une fois.

- On va prendre comme objets du topos, des couples constitués par (X,l), au sens où on vient de définir l.

- Une flèche : . On va prendre des flèches dont on va dire qu’elles préservent des actions :

On dira que f est une flèche de (X,l) vers (Y,µ) si : 1) c’est une flèche de X vers Y ; 2) le diagramme commute : µ o f = f o l

Donc, on ne prendra comme flèches de la catégorie que les flèches qui conservent les actions. Il faut montrer que ces flèches sont associatives, et que pour tout objet, on a des flèches identiques.

Cela nous définit une catégorie. Ce qui est très intéressant, c’est que cette catégorie est un topos.

Pour démontrer qu’une catégorie est un topos, il faut démontrer :

1) Qu’elle admet toutes les limites de diagrammes finis, et les co-limites (il suffit de démontrer qu’elle a un objet terminal et les pull-back pour démontrer qu’elle admet les limites, et qu’elle a un objet initial et les push-out pour démontrer qu’elle admet les co-limites) ;

2) Qu’il y a l’exponentiation ;

3) Qu’il y a un objet central.

On va le faire sur des choses simples :

• Un objet terminal, c’est n’importe quel singleton avec la fonction identité. Or, c’est bien un objet :

Pour démontrer que c’est bien un objet terminal, il faut démontrer qu’il n’y a qu’une seule flèche qui va vers cet objet.

Un singleton, dans le topos des ensembles, est un objet terminal.

Il reste à montrer que le diagramme commute : c’est trivial.

Donc, f est bien une flèche de la catégorie, et elle est unique. Donc, nous pouvons dire : pour tout objet, et son action, il existe une seule flèche vers {a}.

Un objet initial, ce sera (Ø, fØ) qui va fonctionner vers tout objet (X,l).

On va en venir à la seule chose vraiment intéressante : l’objet central.

Remarque préliminaire : il est certain que l’objet initial est vide (il n’y a pas de flèche de 1 vers lui). Donc, le vide est vide.

Prenons un X (non vide) et une action l :

S’il existe une flèche qui fait commuter ce diagramme, X est non vide. Soit x Î X, et considérons l(x) Î X. Nous prenons comme fonction : f(a) = l(x) l o f = l (f(a)) = l(l(x)) = l(x) Dans l’autre sens, on tombe sur l(x).

Donc, cette flèche est une flèche de la catégorie et elle existe toujours si l’objet n’est pas vide. Donc, le vide est unique, dans cette catégorie.

Considérons la question de l’objet central. L’objet central va être construit comme un ensemble et une action, puisque c’est un objet du topos :

w va être ainsi défini : w(Æ) = Æ

w(1) = w(2) = 2

Donc w est bien une action.

C, ça va être l’objet central. Pour avoir un objet central, il faut aussi une flèche vraie vers cet objet central. Une flèche vraie, c’est un élément de l’objet central.

On va prendre comme flèche : f(a) = 2. C’est un élément de l’objet central.

Considérons la flèche g(a) = Ø : C’est une flèche du topos. C’est la flèche faux : F.

Y a-t-il une autre flèche élémentaire de l’objet central ? La seule possibilité serait une flèche qui donnerait à {a} la valeur 1. Or, ça ne marche pas. Donc, il n’y a que deux éléments de l’objet central, à savoir la fonction V qui à {a} assigne le 2, et la fonction F qui à {a} assigne le Ø. Il en résulte que le topos est bivalent.

Esquisse de plan de la suite de la démonstration :

Nous avons défini une catégorie. On peut montrer qu’elle a les limites et les co-limites.

On peut exhiber un objet central de cette catégorie qui n’a que deux éléments (nous n’avons pas encore montré que ça fonctionne comme objet central, c’est-à-dire que ça centre tout monomorphisme). Ensuite, on montre que ce topos n’est pas classique, c’est-à-dire que 1+1 n’y est pas isomorphe à l’objet central. Ensuite, on montre qu’il n’est pas bien pointé, — ça va de pair —. On a montré qu’il y avait unicité du vide. On va montrer qu’il valide le tiers exclu. Et enfin, que la double négation n’est pas égale à l’identité.

Le point est de se demander comment interpréter un monomorphisme dans un tel topos.[34]

___________

---

[1] Cf. art 29 et suivants de la Monadologie.

[2] 34 : «Principes primitifs qui ne sauraient être prouvés, et n’en ont point besoin. Ce sont des énonciations identiques dont l’opposé contient une contradiction expresse» .

[3] Le § 43 est un peu récapitulatif : «Il est vrai qu’en Dieu est non seulement la source des existences, mais encore celle des essences, en tant que réelles, ou de ce qu’il y a de réel dans la possibilité. C’est parce que l’entendement de Dieu est la région des vérités éternelles, ou des idées dont elles dépendent, et que sans lui, il n’y aurait rien de réel dans les possibilités, et non seulement rien d’existant, mais encore rien de possible».

[4] En ce qui concerne ma propre position sur ce point, la décision, voir L’être et l’événement : 20-21-22 ; l’exemple, là, est celui de Pascal.

[5] Le parricide est la soustraction à la loi parménidienne qui se donne comme injonction.

[6] La même recherche que celle de Platon : comment la dialectique, le discours, en tant que mouvement réel de l’être, est-il possible ?

[7] Cf. Livre g.

[8] Merveilleux passage où Hegel montre que le vrai chiffre de la négation, c’est 4 et pas 3. Donc la triplicité hégélienne n’est qu’une apparence. Même chose chez Lacan. L’essence de ce 3, c’est 4.

[9] Incise complémentaire sur Leibniz :

Il y a toujours eu deux options possibles sur Leibniz. On peut mettre l’accent sur la multiplicité descriptible des univers possibles, et sur leur caractère à la fois plié et continu (Deleuze). On peut, au contraire, appréhender Leibniz du point de vue de la décision et de son articulation au principe du meilleur, la fulguration de la limite. Leibniz est celui qui a installé sa pensée au lieu même de l’onto-logie : principe de non-contradiction d’un côté, principe de raison suffisante de l’autre.

[10] Lacan introduit la thèse que si l’espace de référence est fini, alors la négation va fonctionner de façon classique.

[11] Il n’y a, dans le pas-tout, nouvelle négation que si l’espace de référence où tout ça opère touche à l’infini.

[12] L’infini de Lacan est pré-cantorien, parce qu’indéterminé, en quoi, sans doute, il est intuitionniste.

La décision cantorienne est que la pensée de l’infini et la pensée du fini ne sont pas hétérogènes.

La question est de savoir quelle est la charge de négativité du féminin. Lacan propose de dire : c’est une négation singulière qui n’existe que là, qui objecte au tout, qui détotalise quelque chose. Cf. Hegel : «la femme c’est l’ironie de la communauté», figure de détotalisation de quelque chose qui s’affirme comme tout.

[13] Thème où Kierkegaard va venir en incise de Hegel.

[14] Cf. fascicule : définition de 1, objet terminal, p.18-19 ; les raisons pour lesquelles un élément, c’est une flèche de 1 vers un objet, sont discutées p.49-51.

[15] p.23-25 du fascicule.

[16] La question de l’objet central — qui est crucial dans un topos, appelé par les mathématiciens le classifieur de sous-objets — est étudiée au § 14 de la brochure, aux pages 58 et 60.

La négation et le faux sont introduits au § 15, p.60-67.

[17] Vous trouvez ce théorème démontré p.62 - 63. Démonstration à la fois remarquable, simple et très éclairante sur ce que c’est qu’un univers possible.

[18] Antérieurement, toute l’école jésuite portugaise avait beaucoup travaillé dessus.

[19] Le fait qu’il y ait un objet nombre naturel ne se déduit pas de l’identité des topos. Ce n’est pas une propriété générique des topos.

[20] C’est un destin extraordinaire que l’opposition entre indéfini et infini a eu dans l’histoire de la philosophie !

[21] §10 - p. 42-51.

[22] Hamlet essaie de transformer la première question en la seconde. Ne pas être comme sous-ensemble de l’être. Mais le mouvement de la tirade est que ça échoue sur le rêve ; le ne-pas-être est un dormir sans être. Dans le sommeil de l’être, il y a au moins le rêve.

[23] Dans l’univers toposique, l’appartenance est entre flèches, l’inclusion porte sur les objets.

[24] L’équivalence entre deux sous-objets est définie p. 101-103. L’équivalence est une notion constitutive des sous-objets : un sous-objet, c’est une classe d’équivalence de monomorphismes. L’un du sous-objet est évasif.

[25] La singularité — qui est enjeu — est un labeur. Elle va s’installer dans une équivoque. Le communisme des singularités ne peut être que logico-ontologique. La tâche de la singularisation est une tâche complexe, si complexe veut dire logico-ontologique. Il y a toujours quelque chose à faire. Ce n’est pas réglé par la règle.

[26]

Id(N) o m = m

m Õ Id(N)

[27] Est-ce que l’univers de la sexuation est bien pointé ? Est-ce qu’il n’y a qu’un seul vide ? Est-ce qu’on peut dire que toute différence suppose qu’un des termes soit non vide ? Si on admet qu’un élément, c’est le marquage par l’un, cela signifie-t-il qu’un des termes au moins est marqué par l’un ? Est-ce qu’il y a sens à parler de, et que signifierait, l’unicité du vide ?

[28] Encore une fois, rien n’empêche le 2 d’avoir d’autres éléments.

[29] A titre de paradigme, la question du rapport entre le 2 et la différence dans la question de la différence des sexes. Que signifie différence , et le rapport entre cette différence et l’énoncé : il y a deux sexes. On tombe dans des chicanes complexes. Ce qui nomme ça, c’est homme et femme. Homme et femme ne permet pas de penser la différence. Ni non plus la distribution extensionnelle. Si l’on veut penser ce que veulent dire les mots homme et femme, on est au croisement du 2 et de la différence. Dans quel topos sont homme et femme ? Est-ce que la logique de ce topos est classique ? Est-ce que la différence dont il est question est pertinente pour un compte pour deux ?

[30] Est-ce que le phallus ne peut pas être pensé comme limite du 1 et 1 ? Le point est que le phallus détermine la différence, mais aussi qu’il est toujours inscrit dans la différence (dans la position masculine). Chez Lacan, il y a un terme qui est opératoire de la différenciation, mais qui est aussi interne à la différenciation.

[31] Ce qui caractérise le bien pointé, c’est unicité du vide + classissisme. C’est une corrélation logico-ontologique.

[32] Ce qui prouve que la question du tiers-exclu n’identifie pas le classissisme.

[33] Alors que, dans un topos classique, la double négation est toujours égale à l’identité.

[34] Questions pour l’année prochaine :

Comment peut-on donner sens, de l’intérieur d’un univers, à ce que c’est que la topologie ?

La question de la définition de ce que c’est que la topologie commande la question de la vérité, — le caractère global ou local de la vérité —. C’est une question qui éclaire à nouveau la question du statut de la négation. La négation de la négation peut et doit être considérée, dans un topos, comme un opérateur topologique. Quel est le statut d’énoncés du type : «il est vrai localement que...» ?