Séminaire sur la théorie
des catégories
par Alain Badiou (1993-1994)
(Notes de Daniel Fischer)
20.11.93 1
Structures d'ordre 5
Logique générale de l'être et structure de l'Un 8
ALGEBRE DE 1 12
L'ordre partiel sur 1............................................................................................................ 12
Structure dialectique du Topos bien pointé 13
Algèbre de 1 (suite) 15
Intersection, union, complément......................................................................................... 15
L'intersection de deux sous-objets...................................................................................... 15
L'union de deux sous-objets de 1....................................................................................... 15
Le complément d'un sous-objet de 1................................................................................... 16
20.11.93
J'ai proposé l'année dernière (cf.
21.11.92) une présentation du rapport entre la théorie des ensembles et la théorie
des catégories qui différait de celle que j'avais donnée initialement (et dans
laquelle les deux théories apparaissaient comme deux entreprises concurrentes
de fondation du langage mathématique). Ma nouvelle thèse s'énonce ainsi :
- la théorie des ensembles relève de la
décision ontologique, elle prescrit un univers;
elle ne contient pas le concept d'univers, qu'elle ne fait qu'effectuer.
- la théorie des catégories est un
protocole de description des univers possibles; la prescription ontologique (la décision
d'existence) y est en un certain sens suspendue.
Il n'y a donc pas, dans ma nouvelle présentation,
d'unité de plan entre les deux théories, dont la visée propre n'est pas la même.
La question de savoir si, au sein des univers possibles décrits par la théorie
des catégories, la théorie des ensembles est ou non le meilleur (au sens
du meilleur des mondes tel que le fulgure le Dieu de Leibniz) est une question
distincte, qui ne remet pas en cause la pertinence de cette nouvelle présentation.
Redonnons les principaux traits de
l'option ontologique qui caractérise la théorie des ensembles (qui demeure, selon moi, celle
d'un matérialisme absolu de type démocritéen ou lucrècien).
1. L'être ne se laisse penser, en tant
qu'être, que comme multiplicité pure, multiplicité sans autre attribut que son être-multiple.
Ou encore : L'Un n'est pas; il y a un étalement multiple qui n'est jamais
subsumable sous une figure canonique de l'Un. Pas de principe ultime, pas d'étant
suprême, pas de transcendance, ce dispositif est radicalement soustrait à ce
que Heidegger nomme l'onto-théologie (il est d'autant plus frappant que
celui-ci ait totalement omis dans ses textes jusqu'à la mention des noms de Démocrite,
Epicure et Lucrèce; l'existence de cette filière philosophique contredit à elle
seule la reconstitution de l'histoire de la métaphysique qu'il a proposée).
1'. Il n'existe
aucun constituant élémentaire du multiple, aucune atomistique qualitative,
aucune unité dont le multiple serait la composition. Ou encore : tout multiple
est à son tour multiple de multiples.
2. Tout multiple est actuel ; la préexistence
de la possibilité comme puissance, i.e. l'opposition aristotélicienne de la
puissance et de l'acte (et la problématique de l'actualisation qui
l'accompagne) est éradiquée. Il n'y a pas de virtuel. Le possible n'est pas un virtuel, mais plutôt une possibilité
de l'actuel. Conception qui est en conflit avec celle de G. Deleuze, mais qui
renoue avec Platon (l'Idée platonicienne n'a rien de virtuel).
3. Toute différence est localement
assignable (si deux multiples sont différents, alors il existe un repérage
local, ou en point, de cette différence). C'est ce qu'implique l'axiome
d'extensionnalité. Car si deux
ensembles ne sont égaux que s'ils ont les mêmes éléments, il en résulte que
deux ensembles sont différents si un élément au moins appartient à l'un et pas à
l'autre. Vous concluez donc toujours, quant à une différence globale (entre
deux ensembles), à partir d'une différence locale (la monstration d'un élément qui entre dans la présentation de
l'un, et non dans celle de l'autre). L'opposition est ici à nouveau avec
Deleuze (les différences sont chez lui de l'ordre de la flexion globale) et,
au-delà, avec Bergson : c'est l'opposition d'un type de multiplicités composées
d'éléments à un type de multiplicités qualitatives qui supposent une intuition
globale de ce qu'elles sont.
4. Le point d'arrêt
de la composition du multiple comme multiple de multiples ne pouvant être l'un,
ou l'unité, est le multiple de rien, soit l'ensemble vide, qui est ultimement
le seul nom propre de l'être. Il n'y a pas de fond, ni de fondement, aucune espèce
de qualité première ou de matière primordiale dont l'actualisation constituerait
la réalité. Il n'y a pas de chaos, pas de désordre premier. A noter que le vide
est déjà le mot utilisé par les atomistes grecs, ce qu'ils avaient trouvé de
mieux pour désigner le fond le plus dépourvu de fond qui soit. De l'axiome
d'extensionnalité s'infère aussitôt l'unicité du vide. Car le vide est
ce qui n'expose nul élément, et donc son différer d'avec un "autre
vide" est impensable.
5. L'être n'impose aucune clause de finitude.
Il existe certes des multiplicités finies, mais le cas le plus général est
celui des multiplicités infinies actuelles. Comme l'avait vu Descartes,
l'infini est, dès que pensé comme dimension de l'être-multiple, plus clair et
plus distinct que le fini.
L'infini n'est pas l'Un (puisque l'Un n'est pas), mais se présente en
outre lui-même comme ramifié à l'infini en multiplicités. Cette banalisation de
l'infini, que nous devons à Cantor, est un trait anti-théologique : elle signifie
que l'infini n'est pas lié organiquement à l'Un, qu'il n'est en rien
principiel.
Il y a une autre
thèse encore, laquelle est en réalité un théorème qu'on peut déduire des
axiomes fondamentaux de la théorie des ensembles, et donc des principes de
l'ontologie du multiple : il n'existe pas d'ensemble de tous les ensembles.
La pensée de l'être
quand elle est pensée d'un univers ainsi constitué est la mathématique en tant
qu'elle fonctionne dans son cadre ensembliste. Ce qui est opaque dans un tel
univers sans qualités, c'est l'enchevêtrement des multiplicités; l'opération de
la mathématique revient dès lors à désenchevêtrer les multiplicités (c'est en
cela que consistent ses démonstrations).
* un objet
en mathématique ensembliste est une multiplicité complexe; ainsi le nombre
3 est un ensemble composé de l'ensemble vide, du singleton du vide, et de
l'ensemble constitué de l'ensemble vide et de son singleton - i.e. des
occurrences du vide tissées par des opérations et des ponctuations, et en définitive,
une multiplicité tissée du seul vide (c'est pourquoi les objets de la mathématique
ensembliste sont radicalement sans qualités : leur analyse, au sens de la séparation
des éléments de cette multiplicité, ne redonnera jamais que du vide, i.e. aucun
ingrédient qualitativement différencié). L'univers de l'ensemblisme est
ontologiquement homogène, en tant que tissé du seul vide, tandis qu'il est opératoirement
complexe.
* une structure
en mathématique ensembliste est un type possible d'enchevêtrement de
multiplicités. Elle se laisse décrire, par une sorte de phénoménologie de la
pensée ensembliste dans son effectivité, de la façon suivante :
par des théorèmes
d'existence : telle multiplicité complexe doit exister; elle est contrainte à
l'existence par l'univers qui a été décidé : si elle n'existait pas, l'univers
serait contradictoire ou inconsistant (la démonstration de ces théorèmes
d'existence recourt d'ailleurs le plus souvent au raisonnement par l'absurde).
Les théorèmes d'existence engagent quelque chose de l'univers en son entier,
mais celui-ci est testé en un point : ils constituent un plan d'épreuve local
de la consistance de l'univers.
par des théorèmes
de dimension : un objet se voit assigné une dimension nécessaire eu égard à l'univers décidé
(multiplicité finie, infinie, ou plus précisément : de telle finitude, de telle
infinitude). Un exemple de théorème de dimension connu depuis les Grecs est :
les nombres premiers constituent un ensemble infini (dans une formulation bien
entendu différente).
par des théorèmes
de présentation : tout enchevêtrement de multiples d'un type déterminé est
isomorphe à un de ses cas (qui est un objet ou un groupe d'objets); un cas de
tel type les exprime tous. La structure est présentée dans une objectivation
singulière. Exemple : une algèbre de Boole se laisse présenter comme algèbre
des parties d'un ensemble (théorème de Stone).
par des théorèmes
d'identification : une famille d'objets ou une structure a en commun une formule
ou un trait qui identifie les multiplicités qui la composent; le désenchevêtrement
consiste ici à "trouver le lieu et la formule".
par des théorèmes
de décomposition : une structure se laisse analyser en opérations combinant
des structures plus simples; c'est l'analyse au sens cartésien.
Telle est la phénoménologie
élémentaire de l'activité mathématique sous prescription ensembliste; elle tend, par des procédures qui visent à
la simplification, à dés-opacifier, à dés-enchevêtrer les multiplicités. Elle établit
ainsi des clairières de l'être, pour emprunter au lexique heideggerien; ce ne
sont cependant que des éclaircies locales : le desenchevêtrement a certes
tendanciellement le vide pour horizon en raison du caractère homogène de la présentation,
mais il n'opère effectivement que sur des segments de la présentation qui sont
très loin "en aval" de lui. Je dirais que l'éclaircie de la présentation
est polarisée par
l'imprésenté (i.e. le vide).
La théorie des
catégories ne reprend aucune des thèses de
l'ontologie ensembliste.
1. Un objet n'y est
identifié (y compris en ce qui concerne sa "quasi-immanence", ses
sous-objets) que par ses relations externes avec d'autres objets de l'univers
(les flèches).
2. Une différence
(entre deux objets, entre deux flèches) peut parfaitement n'avoir aucune assignation
élémentaire, être purement globale et qualitative (voire être une simple différence
littérale, comme dans le cas de deux objets isomorphes).
3. Il peut exister
plusieurs objets vides (ontologiquement vides, sans éléments),
"plusieurs" étant ici pris au sens catégoriel : plusieurs vides non
isomorphes.
La
pensée catégoricienne n'est nullement une prescription d'univers, mais en
quelque sorte un dispositif expérimental dont le fonctionnement consiste à
spectrographier les décisions ontologiques; et elle le fait du point des contraintes
logiques intérieures à ces décisions et inaperçues par elles : la théorie des
catégories est un appareil de monstration qui montre quelque chose des décisions
ontologiques possibles, quelque chose qui les contraint, mais qu'elles ne
peuvent pas dire, bien que cela leur soit immanent. Elle est d'essence géométrique (ou
diagrammatique), car sa destination principale est de montrer, plutôt que de démontrer.
Cette opposition du montrer et du dire
n'est pas sans analogie avec la pensée de Wittgenstein: "Sur cela, dont il
est impossible de parler, il n'y a qu'à faire silence" (TLP 7.) La théorie
des catégories serait le lieu de monstration silencieuse de l'indicible des décisions
ontologiques; et comme la dimension du montrer est irréductible à celle du
dire, on comprend pourquoi les deux théories ne sont pas réellement en rivalité.
La capacité d'éclaircie réflexive de la
théorie des catégories est exemplifiée par un théorème qui dit en substance : si
un Topos admet la localisation de toute différence (comme le fait l'univers
des ensembles), alors le vide est unique, et il est forcément en position
initiale. La théorie des catégories change ainsi une caractéristique
observable de l'univers de pensée ensembliste en une loi logique applicable à
"tous" les univers possibles qui "ressemblent", quant à tel
ou tel principe de pensée, à l'univers ensembliste.
On dira que deux flèches parallèles f et
g différentes sont élémentairement différentes s'il existe un élément x
de leur source qui est tel que fox gox :
![]()
f g fox gox
La flèche élémentaire x sert de validation locale pour la
différence globale entre les actions f et g.
On dira qu'un Topos est bien pointé
si, dans ce Topos, deux flèches parallèles différentes sont toujours élémentairement différentes
(toute différence s'y avère en un point). On peut donc dire qu'un Topos bien
pointé est un univers possible qui "ressemble" à l'univers de
l'ontologie ensembliste en ce qui concerne la thèse sur la différence.
Or, ce qui est admirable est que cette
logique de la différence prescrit aussitôt sa conséquence ontologique : si
un Topos est bien pointé, tout objet vide y est isomorphe à l'objet initial 0.
On démontre ici la connexion générale entre la thèse sur la différence et deux thèses sur le vide: son unicité et sa
position fondatrice (initiale).
démonstration
Soit un Topos bien
pointé, qui ne soit pas un Topos dégénéré. Considérons un objet a non initial
(i.e. qui n'est pas isomorphe à zéro); un tel objet existe nécessairement
puisque le Topos n'est pas dégénéré.
De même existent nécessairement la flèche
O a (qui exprime le caractère initial de 0) et la
flèche Id(a). Ces deux flèches sont des monomorphismes de même cible a; et
comme il n'y a pas d'isomorphisme entre leurs sources (puisque a est supposé
non isomorphe à 0), ces sous-objets sont réellement "deux" : ils ne
sont pas similaires. Ils ont par conséquent des centrations effectivement différentes
(qui, elles aussi, existent nécessairement dans un Topos) et qui sont des flèches
parallèles (puisqu'elles vont de a vers C).
Nous voici donc en situation d'avoir
deux flèches parallèles assurément différentes. Comme notre Topos est bien
pointé, la différence globale de ces deux flèches s'avère obligatoirement par
l'existence d'un élément x de leur source commune qui avère cette différence;
ceci impose que a possède au moins un élément, et par conséquent a n'est pas
vide. Nous avons ainsi démontré que si a
n'est pas isomorphe à zéro, alors il n'est
pas vide. Ce qui se dira aussi bien : s'il est vide, alors il est isomorphe à zéro.
Dans un Topos bien pointé,
"vide" et "zéro" (ou initial) s'avèrent être des concepts
de même extension donc substituables l'un à l'autre. Et comme nous savons qu'il
n'y a qu'un zéro (au sens catégoriel : tous "les" zéros, ou toutes
les lettres qui les nomment, sont isomorphes), il faut en conclure qu'il n'y a
qu'un seul vide.
Ainsi l'unicité fondatrice (initiale) du
vide est-elle l'effet ontologique de la thèse en pensée sur la différence.
Structures d'ordre
Soit un univers
littéralisé (i.e. constitué d'entités marquées par des lettres), et supposons
qu'y soit définie une relation d'ordre (notée et que l'on lira : "plus petit ou égal
à"); elle obéit aux propriétés suivantes :
- réflexivité : x x
- transitivité : si x y et y z, alors x z
- anti-symétrie : si x y et y x, alors x = y
Il s'agit d'une structure d'ordre
partiel : relie certains termes de l'univers, mais d'autres
restent incomparables. On peut citer deux exemples de structures d'ordre
partiel : la relation d'inclusion entre les sous-ensembles d'un ensemble (notée
), et la relation logique d'implication (notée ). Ces deux exemples ne sont pas choisis au
hasard; l'un relève de l'ontologique et l'autre du logique et le fait que la
relation d'ordre leur soit commune laisse supposer qu'elle joue un rôle
fondamental dans la connexion logico-ontologique. Les structures d'ordre
avaient déjà été isolées en tant que telles par Bourbaki, comme s'il y avait là
une dimension singulière de la pensée, irréductible aux structures algébriques
et aux structures topologiques; cette autonomie des structures d'ordre tient en
fait à leur situation d'interface entre l'algèbre et la topologie, de même que,
sans avoir réellement de domaine propre, elles jouent un rôle de médiation
entre le logique et l'ontologique. Nous tâcherons par la suite de comprendre
pourquoi la pauvreté axiomatique de la structure d'ordre ne l'empêche pas
d'exercer une puissance diagonale sur d'autres domaines.
Y a-t-il une transcription catégorielle
possible de la relation d'ordre ? Soit une catégorie ayant la propriété suivante
: il y a au plus une flèche entre deux objets de cette catégorie
(symbolisons une telle flèche
par ).
- Puisque c'est une
catégorie, la flèche identique Id(a) - a objet quelconque - existe nécessairement
et, dans la catégorie particulière que nous considérons, c'est la seule flèche
de a vers a : a a
- Toujours d'après
les réquisits minimaux des catégories, si les objets a, b et c sont reliés
entre eux de telle sorte que a b et b c, alors existe la composée de ces deux flèches,
elle-même unique dans la catégorie considérée : a c. Donc, si a b et b c, alors a c.
- Soit les deux
flèches f et g reliant a et b de la façon suivante :
![]()
g o f = Id(a) - identité évidente puisque dans cette
catégorie bien particulière, il n'y a qu'une seule flèche de a vers a, qui est
Id(a). De même f o g = Id(b); f est donc un isomorphisme et a est isomorphe à
b. Autrement dit : si a b et b a alors a et b sont isomorphes (ce que l'on peut
assimiler à l'égalité dans la propriété d'anti-symétrie).
Si dans une catégorie dotée d'une structure d'ordre, il
existe un objet plus petit que tous les autres (notons le 0), on aura 0 x et il s'agira d'une catégorie à objet initial; de
même s'il y existe un objet plus grand que tous les autres (notons le 1), on
aura x 1 et il s'agira d'une catégorie à objet terminal. Il
s'agit respectivement, si l'on prend la relation comme exemple de structure d'ordre, de l'ensemble
vide et de l'ensemble E lui-même; et s'il s'agit de la relation , du faux (le faux implique possiblement
n'importe quelle proposition de la catégorie, ce que les logiciens du Moyen Age
avaient déjà bien vu : ex falso sequitur quodlibet), et du vrai (une proposition vraie est
véridiquement impliquée indifféremment par une proposition vraie ou par une
proposition fausse); la catégorie "calcul des propositions" s'espace
entre le faux et le vrai (de la même façon que nous avons vu qu'une catégorie à
clôture cartésienne non dégénérée est fibrée par l'axe qui relie 0 et 1); les
autres propositions (celles qui sont situées entre ces deux extrêmes), ce sont
celles qui sont susceptibles d'être vraies ou fausses, celles qui n'ont pas
encore été validées comme fausses ou vraies. Rappelons à ce propos une règle
fondamentale du calcul des propositions qui nous servira souvent : il n'y a
qu'une seule circonstance au cours de laquelle l'implication est fausse, c'est
lorsque l'antécédent est vrai et que la conséquence est fausse (si p est vrai et que q est faux, l'implication p q est fausse).
Pour que cette catégorie admette les produits, il faut qu'y
existe un objet tel que (cf. déf. du produit) : cet objet soit plus petit ou
égal que a et que b; et en outre, soit c un objet quelconque qui soit plus
petit ou égal que a et que b, que c soit plus petit ou égal que l'objet que
nous cherchons à caractériser. Celui-ci est donc le plus grand de tous les
objets plus petits que a et que b. On l'appellera le PGI (pour "plus grand
inférieur de a et de b"). Par dualité, on dira que la catégorie admet les
co-produits, s'il existe un objet qui soit le plus petit de tous ceux qui sont
plus grands que a et que b. On l'appellera PPS (pour "plus petit supérieur
et à a et à b").
En ce qui concerne la relation , l'intersection des sous-ensembles A et B (A B) correspond, en terme catégoriel, au produit (elle
est ce qu'il y a de plus grand dans ce qui est plus petit que A et que B) et l'union
des sous-ensembles A et B (A B) correspond au co-produit (elle est ce qu'il y a de
plus petit dans ce qui est plus grand que A et que B).
Qu'en est-il de la relation ? Ce qui
correspond au produit, c'est la disjonction (le connecteur logique
"et", noté ); en effet, nous cherchons à caractériser une proposition
r telle que :
r p et r q ; soit une proposition t qui implique à la fois p
et q (t p et t q), t r
il est clair que r est
identique à p q
De même, il est aisé de voir qu'au co-produit, correspond la conjonction
(le connecteur logique "ou", noté ); en effet, la proposition r que nous cherchons ici
à caractériser est telle que :
p r et q r ; soit une proposition t impliquée à la fois par p
et par q (p t et q t), r t
r est identique à p q
On appellera catégorie
d'ordre une catégorie
- dont les objets sont reliés entre eux
par une flèche au plus
- possédant un objet initial, un objet
terminal,
- et admettant les produits et les
co-produits.
Une structure d'ordre peut toujours
être représentée comme une catégorie d'ordre.
Dans le champ de l'ontologie, on dira
que, supposé un ensemble E, l'ensemble de ses sous-ensembles est une telle
catégorie (puisque est une structure d'ordre); de même, dans le
champ de la logique, on considérera comme une catégorie de ce type une
catégorie dont les objets sont des propositions et dont les flèches sont des
implications (puisque est une structure d'ordre). Du point de vue
catégoriel, ça ne fait pas de différence. Au fond, la pensée catégorielle ne distingue pas
un univers de discours et un univers d'objets (un univers ontologique). Plus
précisément : elle les accueille dans un univers commun; le génie propre de la
pensée catégorielle est de suspendre l'opposition du logique et de
l'ontologique en tentant d'en donner les figures possibles communes.
En
tout état de cause, une telle catégorie ne saurait être un Topos, puisque dans
ce cas l'Objet Central reçoit deux flèches de l'objet terminal (le vrai et le
faux, qui sont deux flèches différentes). Et pourtant, la structure d'ordre
partiel va contribuer à nous faire comprendre ce que peut être l'ordre dans
un Topos. Fondamentalement, notre
objectif sera de déterminer un concept de l'ordre, une structure, qui permettra
d'étudier les connexions possibles entre ces flèches singulières que sont les
éléments de l'Objet Central - supports, rappelons-le, de l'évaluation logique
dans un Topos
a) Envisageons pour commencer la
question générale de l'ordre entre sous-objets d'un objet quelconque du Topos.
Soit deux sous-objets f et g de b. Ce sont deux
monomorphismes de cible b. Supposons qu'il existe une flèche h telle que le
diagramme suivant commute :
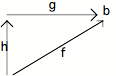
On a g o h = f. On dira alors que f g, ou que f est "inférieure à g", s'il
existe une flèche h telle que g o h = f. Nous allons voir que la relation est une structure d'ordre.
- elle est réflexive de ce que f o Id(a)
=f. On a donc bien f f (Id
(a) est le h qui "factorise" f).
- elle est transitive : le diagramme
suivant exprime que f g, et que g h
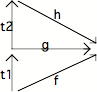
1. g o t1 = f
2. h o t2 = g
3. (h o t2) o t1 =f
4. h o (t2 o t1) = f (par associativité)
L'équation 4. exprime que (t2 o t1)
factorise f par h; et donc f h
Ainsi, si f g et g h, on a f h : la relation est transitive
Les sous-objets d'un objet donné (ou leurs
"représentants", i.e. les monomorphismes de même cible) constituent
donc le site d'une relation d'ordre possible; mieux vaut parler de site plutôt que d'ensemble des sous-objets, car la relation d'ordre excède
peut-être les ressources du compte-pour-un ensembliste (à ce stade en tout cas,
rien ne nous en garantit).
b) La relation est cependant peu maniable pour l'étude des éléments
de C, ce qui est, rappelons-le, le but de notre investigation actuelle;
considérons en effet le diagramme suivant :
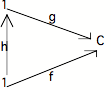
S'il existe h telle que g o h = f, il
faut que cette flèche soit de 1 vers 1. Mais la seule flèche de ce genre est
Id(1). On a donc g o Id(1) = f, soit g = f. Ainsi, le diagramme ne commute que
si f et g sont identiques; si f g, il n'y a pas de relation d'ordre possible entre f
et g, qui sont de ce fait incomparables.
c) Nous allons contourner l'obstacle en considérant les monomorphismes
de cible 1 - notons-les : 1(a); ils
ont nécessairement chacun une centration, de source 1 et de cible C (la
centration de chaque monomorphisme de cible 1 est donc un élément de C). Nous
avons vu, en effet, que tout sous-objet "réel" (non similaire) a une
centration, et, qu'à l'inverse, toute flèche vers C est la centration d'un
sous-objet et d'un seul (théorème crucial du Centre). Par conséquent, il y
a, dans un Topos, autant de monomorphismes de cible 1, qu'il y a d'éléments de
C, i.e. de valeurs logiques du Topos (nous savons qu'il y en a au moins
deux, le vrai et le faux, mais possiblement plus). Autrement dit : étudier les
sous-objets de 1, c'est la même chose qu'étudier les valeurs logiques d'un
Topos, puisque nous venons de voir qu'ils sont en correspondance bi-univoque.
Mais, ce faisant, au lieu d'une représentation élémentaire (les éléments de C)
qui ne permet pas d'introduire la machinerie de l'ordre, nous disposons de la
relation d'ordre qui existe entre les sous-objets de 1 (elle existe
pour les sous-objets d'un objet quelconque, et donc pour les sous-objets de 1).
Ainsi, l'objet terminal 1, par ses
sous-objets, représente en immanence la logique d'un Topos. La clef d'un Topos
comme lieu logique réside dans la structure (relationnelle) des sous-objets de
1, donc des monomorphismes de type a ---- 1, pris comme représentants d'une classe de
similarité. A ce titre, l'étude des sous-objets de 1 est une pièce centrale de
l'investigation logico-ontologique. L'algèbre de 1 développée à partir de cette
étude va donner le poids d'être, le lestage objectal, de la logique du Topos
(le réel du possible que constitue cette logique).
Logique générale de l'être et structure de l'Un
Ce que la théorie des Topos nous dit,
dans un montage transparent, c'est que la logique générale de l'existant, la
logique de ce qu'il y a, est suspendue à une réflexion sur la structure de
l'Un. Idée qui hante les dispositifs monothéistes sous la forme de la question
: comment se fait-il que l'Un, s'il est vraiment l'archi-transcendance du
simple, puisse avoir une structure ?
Il y a toujours eu deux orientations
principales sur cette question :
- pour l'une, l'Un est absolument l'Un; aucun prédicat structurant ne lui est approprié
(en dehors de l'absoluité de l'Un lui-même). La forme ultime de cette
orientation est la théologie négative, pour laquelle l'Un n'est pensable que
selon ce qu'il n'est pas. Plus radicalement encore : l'Un est au-delà de l'être
lui-même; il n'y a par conséquent aucune figure structurale de l'Un autre que
son indiscernabilité ultime au regard du néant.
- pour la seconde orientation au
contraire, l'Un est. Il en découle
que l'Un est appropriable dans une disposition structurée quelconque; non
seulement des prédicats lui conviennent, mais encore des divisions internes à
l'Un sont pensables, qui n'empêchent pas l'Un de perdurer comme Un dans sa
scission même. On aura ici reconnu en particulier les montages trinitaires
fleurissant à l'ombre des monothéismes.
Le Parémnide
Nous allons considérer le traitement de
cette question dans le Parménide;
je vais tenter, ce faisant, de vous expliquer pourquoi je pense que ce dialogue
de Platon est historiquement le premier texte de philosophie catégorielle.
1
Au début du dialogue, le jeune Socrate
réfute le discours que tient Zénon en lui reprochant de n'avoir pas donné une
localisation du pensable : Socrate introduit à cet endroit la théorie des Idées
précisément parce que le lieu du pensable n'est pas selon lui là où le voit
Zénon. Curieusement, le vieux Parménide semble soutenir les efforts du jeune
Socrate contre le champion officiel des thèses éléates qu'est Zénon, dont
l'argumentation ne semble pas ici constituer une défense adéquate de la position
de Parménide. Celui-ci déclare même à Socrate que son audace n'est pas assez
grande, qu'il ne va pas assez loin : il faut en effet, selon lui, admettre les
Idées de tout, pas seulement
l'Idée de vertu, mais aussi l'Idée de la boue, l'Idée du cheveu ... L'Idée
désigne ici la pensabilité en général et constitue la réponse à la question
"que pense la pensée ?" ou encore "à quelles conditions la
pensée s'empare-t-elle du pensable ?". Pour conquérir l'audace que préconise
Parménide, il faut s'exercer, et si Socrate est insuffisant dans la tâche qu'il
se propose, c'est qu'il est encore trop jeune.
Le texte du Parménide va dès lors s'infléchir vers un examen de type logique, car la notion
d'exercice véhicule celle de possibilités de la pensée, posées indépendamment
de la question : "qu'est-ce que la pensée décide ?". Dans l'ensemble
du dispositif platonicien, le Parménide est en quelque sorte un dialogue non-axiomatique, si par axiome
on entend une décision constituante. En effet, ce n'est pas exactement vers une
axiomatique de l'Un que va s'engager le dialogue; il n'est que de le comparer
avec le surgissement de l'Idée du Bien dans La République pour s'en convaincre : le recours à l'élément
poétique (la métaphore du soleil), l'absence de réseau catégoriel, y installent
l'Idée du Bien dans la singularité de sa transcendance pure et soulignent le
caractère de décision que revêt sa surrection. Dans Le Parménide, au contraire, aucune intuition simple de l'Un n'est
proposée, et encore moins une image.
2
Lisons à partir de 135 e jusqu'à 136 c : "Supposer, en
chaque cas, l'existence de l'objet et considérer ce qui résulte de l'hypothèse
ne suffit pas. Il faut supposer aussi l'inexistence du même objet, si tu veux
pousser à fond ta gymnastique ... En un mot, pour tout ce dont tu poseras ou
l'existence ou la non-existence ou toute autre détermination, examiner quelles
conséquences en résultent, d'abord relativement à l'objet posé, ensuite
relativement aux autres : l'un quelconque, d'abord, à ton choix, puis
plusieurs, puis tous. Tu mettras de même les autres en relation et avec
eux-mêmes et avec l'objet à chaque fois posé, que tu l'aies supposé exister ou
non-exister. Ainsi t'exerceras-tu, si tu veux, parfaitement entraîné, être capable
de discerner à coup sûr la vérité".
Comment procéder si l'on veut
"discerner à coup sûr la vérité" ? On considère quelque chose
dont on pose l'existence et aussi la non-existence; puis on examine les
conséquences qui résultent de cette existence ainsi que celles qui résultent de
cette non-existence, par rapport à ce quelque chose lui-même, et par rapport
aux autres choses. Ce qui nous donne 4 examens :
conséquences par rapport à
lui-même
[DN1] existe
conséquences par rapport aux autres
x
conséquences par rapport à lui-même
n'existe pas
conséquences par rapport aux autres
Il faut encore procéder en sens inverse,
i.e. considérer les objets autres que x sous la supposition que x existe, puis
sous celle que x n'existe pas, et ce dans leur rapport à eux-mêmes et dans leur
rapport à x
par rapport à eux-mêmes
x existe
par rapport à x
autres que x
par rapport à eux-mêmes
x n'existe pas
par rapport à x
Ce qui nous donne 4 + 4 hypothèses (or,
on sait que le déploiement du Parménide propose 9 hypothèses; ce bouclage de la pensée par l'hypothèse-en-plus
est un illustre exemple de ce que je nommerai volontiers la méthode diagonale
de Platon, et dont je vous entretiendrai peut-être un jour). Ces passages du Parménide désignent une méthode d'exhaustion logique, une
"matrice des matrices" (F. Regnault : Dialectique d'épistémologies Cahiers pour l'analyse n° 9 p. 46); il s'agit d'un
pur exercice de "gymnastique" : on ne part pas d'une assertion
privilégiée concernant x, mais on considère le système des possibilités inhérentes
à x. Ce dont il s'agit, c'est de fictionner la catégorie (de) x
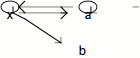
Les "rapports" - de x à
lui-même, de x aux autres - sont figurés dans cette catégorie par des flèches
relationnelles.
Pour qu'un exercice effectif ait lieu,
il faut que Parménide pose lui-même une hypothèse : "N'êtes-vous point
d'avis plutôt, le parti une fois pris de jouer ce jeu laborieux, que je
commence par moi-même et par ma propre hypothèse et que, posant, à propos de
l'Un en soi, ou qu'il est ou qu'il n'est pas un, j'examine ce qui doit en résulter" (137 b). C'est de ce choix que résultent les (8 ou) 9
hypothèses de la fin du texte. Le Parménide est au fond un exercice au sujet de l'Un qui n'a pas
d'autre enjeu que de tisser le réseau de la catégorie (de) x.
3
Relisons 136 b : pour tout ce dont tu
poseras ou l'existence ou la non-existence ou toute autre détermination. L'existence n'est pas ici ce dont on part, ce dont on
décide, mais, au même titre que la non-existence ou toute autre détermination,
ce qui est traité comme une propriété
possible de l'entité considérée.
Or, c'est très précisément cela -
considérer l'existence comme une propriété - que n'admettait pas Kant, dans sa
(tentative de) réfutation de Descartes (CRP Dialectique transcendantale chap. II, 4ème section : de l'impossibilité d'une
preuve ontologique de l'existence de Dieu). Selon lui, Descartes, dans la 5ème Méditation métaphysique, considère abusivement l'existence comme une
propriété de Dieu, alors que ces types de donation de l'objet que sont le
concept et l'existence sont hétérogènes, intransitifs, et que l'on ne peut
passer de l'un à l'autre : il faut radicalement séparer la conformité aux conditions
générales de la connaissance possible et l'inscription dans la totalité de
l'expérience. L'existence est une donation irréductible. Si on traite l'existence
comme une propriété, on établit une indiscernabilité entre existence et possibilité;
Descartes n'aurait, selon Kant, établi que ceci : l'existence de Dieu est
possible, mais non que Dieu existe. Kant est en réalité pris dans une
conception empiriste de l'existence : l'existence est ce qui se donne, ce qui
ne peut que se constater, l'improuvable même; c'est le seul point qui ne relève
pas de la constitution transcendantale. Concernant les "idées transcendantales"
(les concepts auxquels aucun objet ne correspond dans la réalité), on peut supposer leur existence - c'est même bien utile dans le cas de
Dieu, en vue d'un usage purement régulateur, et cela devient alors un postulat
de la raison pratique - mais rien ne peut les justifier, car pour justifier des idées, en faire un réel, il
n'y a pas d'autre recours que l'expérience.
L'indiscernabilité de l'existence et de
la possibilité, rappelons-le, c'est ce qui définit la logique :
l'existence des objets de la pensée pure, en tant qu'indiscernable de leur
possibilité, est une existence purement logique.
Pour le Platon du Parménide (laissons pour l'instant Descartes de côté), les deux
options - l'Un existe, l'Un n'existe pas - peuvent être différenciées par leurs
conséquences pour la pensée. On peut prendre pour axiome que l'Un existe, comme
on peut prendre pour axiome que l'Un n'existe pas; si l'examen des conséquences
de ces deux axiomes montre des effets différents pour la pensée (consistance ou
inconsistance), alors il faut poser que l'existence doit être traitée comme une
propriété (de l'Un).
La conception dualiste de Kant (le
couple pensée pure / expérience) est étrangère à Platon; le couple qui fonctionne
chez ce dernier - décision / consistance (ou non) des effets - le maintient sur
une unité de plan et ce monisme est le point de ce qu'il ne faut pas
craindre d'appeler son matérialisme.
Pour Platon, la décision prise, on est comptable des effets entiers de cette
décision, que ceux-ci affectent le pensable pur ou l'expérience, sans
distinction (l'Idée de triangle ou bien l'Idée de boue), et l'on doit en
examiner le réseau. Il s'agit dans
le Parménide de constituer le réseau
de l'Un, en examinant, quant à leur consistance, les effets induits par la
décision concernant l'existence de l'Un et ceux qui sont induits par la
décision concernant son inexistence. La norme pour cette évaluation est de
nature mathématique, et ce paradigme institue un seul champ homogène du pensable.
4
Très catégorielle d'inspiration est
également l'idée selon laquelle l'identité n'est pas une qualité substantielle,
mais une relation de soi à soi qui va être examinée sur le même plan que la
relation de soi aux autres. La détermination identitaire va en outre être
examinée sous la supposition de l'existence ou de la non-existence de l'entité
en question, ce qui nous livre ici une thématique "existentialiste"
avant la lettre (on part de la détermination d'existence pour n'aboutir qu'en
second lieu à la détermination d'identité).
L'un doit être distingué de l'identique
: "Parménide : La nature de l'un n'est point celle du même. Aristote :
Quelle est la différence ? Parménide : C'est que, lorsqu'une chose devient la
même qu'une autre, elle ne devient pas une. Aristote : Eh bien, que s'ensuit-il
? Parménide : Ce qui est devenu le même que plusieurs doit nécessairement
devenir plusieurs, et non pas un. Aristote : C'est vrai" (139 d). En théorie des catégories aussi, nous le
savons, plusieurs objets littéralement différents peuvent être catégoriellement
identiques (objets isomorphes); ce qui spécifie l'identité catégorielle, c'est
le réseau d'actions dans lequel est pris un objet.
Enfin, l'Un va être la localisation
paradigmatique de la vérité (conformément à l'esprit catégoriel suivant lequel
la vérité est une détermination locale pensée dans un réseau global) : l'Un est
la clef logique du champ du pensable (celui-ci se constitue de ce qu'ont été
posés l'existence ou la non-existence de l'Un), tandis que c'est la structure
de 1 qui donne la clef logique du Topos.
5
En définitive, l'enjeu du Parménide est de savoir quel est le champ de possibilité du
pensable. On en connaît la conclusion négative, qui formulée en termes catégoriels,
se dira : la catégorie (de) x est inconsistante; ou encore : il n'y a pas de
Topos du pensable. Ainsi, l'exercice platonicien sur l'exhaustion logique d'un
être indéterminé saisi comme Un délivre une catégorie inconsistante. La fin du Parménide en fait un dialogue aporétique. Ce qui signifie
que, pour Platon, il n'y a pas de structure de l'Un (thèse dont le néo-platonisme s'est nourri pendant des
siècles); ce n'est pas que l'Un soit impensable, mais plutôt : sa pensée n'est pas dans la figure de la
structuration (logique). La logique est l'exercice de la pensée, elle ne
saurait en être le point de départ. Ce dont il faut partir c'est d'une décision;
décider est cela seul qui institue une consistance du pensable. Il faut donc
dire : "Il y a de l'Un"
(ainsi que le fait Lacan quand il épingle cette formule au symbolique comme à
son principe). L'Un est décidé et de la sorte il est dessoudé de toute
possibilité, il est autre chose que le remplissement de la possibilité qu'il y
a l'Un (et il est aussi autre chose que la réfutation de la possibilité que
l'Un n'est pas). "Il y a de l'Un" est un axiome. La décision
ontologique précède la logique. C'est pourquoi Platon est véritablement le fils
de Parménide (quitte à commettre à son endroit le parricide dans le Sophiste); et c'est parce que Zénon est celui qui argumente
sur les possibilités qu'il est présenté comme son disciple infidèle. La
thèse de l'Un - c'est le
"message" du Parménide -
n'est pas argumentable sur horizon de possibilité.
La théorie des Topos soutient au
contraire (cf. fin du chapitre "Structures d'ordre"), qu'il y a bien
une structure de l'Un comme détermination logique de l'univers (nous retrouvons
à nouveau sa dimension anti-platonicienne). On pourrait faire une objection à
ce rapprochement entre l'Un platonicien et l'Un toposique. Celui-ci est un Un
positionnel (il est caractérisé comme objet terminal) plutôt qu'un Un
intrinsèque; y a-t-il vraiment là autre chose qu'une simple homonymie ? Je
tenterai de justifier néanmoins ce rapprochement par les remarques suivantes :
* Le Un toposique (1) n'est pas vide :
il a un élément - 1 ----Id(1)---- 1 - et cet élément c'est lui-même; il y a là une
unicité d'appartenance à soi-même qui "tire" le 1 vers l'intrinsèque.
1 est aussi ce qui prescrit l'élémentaire
- 1 ------ a -; chiffrage qui est sa caractérisation atomique.
* en outre 1 est catégoriellement unique
(à supposer qu'il y ait deux objets terminaux, ils sont, nous l'avons vu,
isomorphes).
* 1 est un annulateur universel des
différences élémentaires en a
1 ----e1- a -----f ----- 1
e2
1
supposons que les éléments e1 et e2
soient différents
f existe nécessairement (puisque 1 est
objet terminal)
or : f o e1 = f o e2 = Id(1); f fonctionne donc comme co-égalisateur de
e1 et de e2 (en toute rigueur, il faudrait, pour pouvoir l'affirmer, démontrer,
ce qui est aisé, que, soit un objet b cible d'une flèche unique dont la source
est 1, le triangle a-1-b commute).
* enfin 1 touche à la vérité : dans le
pullback qui définit l'Objet Central, on voit clairement que toute différence
assignable (tout monomorphisme de source a) s'analyse (c'est la fonction de
centration) du point de 1 (et plus précisément du compte-pour-un de l'objet a :
1(a)) et de la vérité).
Cette série de déterminations
intrinsèques explique que, après tout, l'Un toposique mérite bien son nom.
Algèbre de 1
L'ordre partiel sur 1
Notre objectif, qui est de determiner un
concept de l'ordre entre les éléments de l'Objet Central - i.e. ultimement de
savoir ce que peut être un ordre, une structure, qui concerne les supports de
l'évaluation logique dans un Topos - nous impose, nous l'avons vu, le recours
aux monomorphismes de cible 1.
Considérons le diagramme suivant :
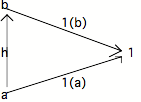
La flèche 1(b) o h est une flèche de a
vers 1. Or, il n'existe qu'une seule flèche de a vers 1 (1 objet terminal), qui
est 1(a). Donc le diagramme commute, et l'on a 1(a) 1(b). On voit par conséquent que deux sous-objets de
1 sont toujours comparables s'il existe une flèche h entre leurs sources.
Ou encore : parmi les sous-objets de 1, l'existence d'une relation d'ordre
entre 1(a) et 1(b) est strictement identique à l'existence d'une flèche entre a
et b, ou b et a. Philosophiquement : deux sous-objets de 1 sont ordonnés dès
que liés par une action. Seuls sont incomparables quant à l'ordre les
sous-objets 1(a) et 1(b) tels qu'il n'existe aucune flèche entre a et b (tels
donc que ces objets sont catégoriellement disjoints ou non reliés).
Examinons maintenant le sous-objet de 1
tout particulier qu'est la flèche 0 ----- 1.
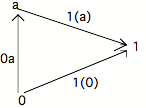
La flèche 1(a) o 0a est une flèche de 0
vers 1, donc est forcément la flèche 1(0). Le diagramme commute et l'on a 1(0) 1(a). Ainsi la flèche 1(0) est-elle parmi les
sous-objets de 1 toujours "inférieure" à tout autre sous-objet 1(a).
Nous dirons que le sous-objet de 1 qu'est 1(0) est un minimum pour la
relation d'ordre.
Examinons maintenant le sous-objet de 1
non moins particulier qu'est la flèche 1 ---- 1, ou Id(1).
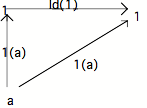
Ce diagramme montre que l'on a toujours
1(a) Id(1). Il suffit de remarquer que toutes les flèches
de ce diagramme existent nécessairement, et que Id(1) o 1(a) = 1(a) pour que la
conclusion s'impose. Nous dirons que le sous-objet Id(1) de 1 est un maximum
pour la relation d'ordre.
Finalement : il existe sur les sous-objets de 1 une relation d'ordre
partiel, effective entre a et b dès qu'existe une flèche entre a et b, qui a
1(0) pour minimum et Id(1) pour maximum.
Nous savons que le vrai est la
centration de la flèche Id(1) et que le faux est la centration de la flèche 1(0).
De ce que 1(0) soit un minimum pour la relation d'ordre, et de ce que Id(1) en
soit un maximum, il résulte (puisqu'il existe une relation biunivoque entre les
sous-objets de 1 et leur centration) que le faux est la valeur de vérité minimale
et que le vrai est la valeur de vérité maximale. Le vrai et le faux ne sont que
des limites et les différentes valeurs de vérité possibles s'espacent entre le
vrai et le faux, ouvrant à une logique de l'approximation, de la nuance. Si les
valeurs de vérité sont au nombre de deux (Topos bivalent), le vrai et le faux
épuisent les valeurs de vérité possibles - avec, il est aisé de le montrer,
1(0) Id(1) : la valeur de vérité du faux est inférieure à
celle du vrai (!). Il n'y a pas ici de spectre des valeurs de vérité, celles-ci
ne se présentent pas comme des limites. Un Topos bivalent, dont le modèle
canonique est la catégorie des ensembles, n'ouvre pas à une logique de
l'approximation, mais à une logique de la décision : entre le vrai et le faux,
il y a un choix à faire (il n'y a pas de troisième terme : le tiers est
exclu).
Structure dialectique du Topos bien pointé
Nous avons vu qu'un
Topos bien pointé est un Topos dans lequel deux flèches parallèles f et
g différentes possèdent toujours un élément x de leur source qui est tel que
fox gox. Un Topos bien pointé obéit
à l'axiome d'extensionnalité (c'est exemplairement le cas du Topos des
ensembles). Dans une conception extensionnelle toute différence globale a un
test local; les différences ne sont pas appréhendables par une intuition
différentiante des totalités, mais par un trait. On peut caractériser un tel
Topos en disant qu'il n'y a pas en son sein de différences suffisamment qualitatives
qu'elles ne puissent pas être évaluées en un point, et cette caractéristique
est ce qui homogénéise les multiples de ce Topos.
Les différences
seraient donc de deux types : il y aurait les différences homogènes (celles qui
se laissent élémentairement traiter) et les différences hétérogènes (celles qui
ne se laissent pas élémentairement traiter), ce qui renvoie ultimement à deux
types de multiplicités. C'est précisément la thèse de Deleuze - placée sous le
patronage de Bergson - qu'il existe deux types de multiplicités : une multiplicité
quantitative ou numérique (assignée à la science) et une multiplicité
qualitative, intensive. "Les concepts et les fonctions se présentent ainsi
comme deux types de multiplicités ou variétés qui diffèrent en nature" (Qu'est-ce
que la philosophie ? p.121). Plus exactement, l'être proprement dit est le mouvement de
dicession de ces deux types de multiplicités; ce qui importe donc en dernière
instance c'est le mouvement par lequel les deux types de multiplicités
s'écartent, c'est la bifurcation de l'élan (ce qui explique le primat accordé
en fait à la multiplicité intensive).
L'option ensembliste
est une option résolue pour l'homogène : chaque ensemble est ultimement tissé
du vide, et le vide est par conséquent un principe d'homogénéisation de la
composition immanente de chaque ensemble. L'option dynamique ou vitaliste
(comme l'est celle de Deleuze - Bergson) n'est pas, on le voit, exactement en symétrie
avec la précédente, puisqu'elle subsume l'homogène, elle prétend lui accorder
une place, à côté de l'hétérogène; elle se veut une théorie de la complexité.
Tout Topos bien
pointé est bivalent - c'est un théorème fondamental que nous avons déjà démontré;
autrement dit : dans un Topos bien pointé il n'y a que deux éléments de l'Objet
Central, le vrai et le faux. Ceux-ci étant les centrations de deux
monomorphismes de cible 1 (respectivement 1 ---- 1, et 0 ---- 1), il résulte de la correspondance
biunivoque existant entre élément de C et sous-objet de 1 que, dans un Topos
bien pointé, il n'existe que deux sous-objets de 1 : 1 ---- 1 et 0 ----- 1.
Soit un Topos bien
pointé quelconque et supposons un objet a de ce Topos qui ne soit pas isomorphe
à 0 ni à 1. Considérons la flèche 1(a) : a ----1(a)---- 1, flèche qui existe
nécessairement (puisque 1 est objet terminal). Puisque 1 --- et 0 --- épuisent les sous-objets
possibles de 1 dans ce Topos, a ---1(a)--- 1 n'est pas un monomorphisme. Et
donc, si a est cible de deux flèches parallèles différentes f et g, 1(a) est
astreint à ne pas conserver cette différence dans tous les cas; il
existe donc nécessairement au moins une paire de flèches f et g (parmi toutes
les paires de flèches parallèles de cible a) telle que : si f g, 1(a) o f = 1(a) o g.
Soit un objet c
cible d'une flèche h dont la source est a, avec h o f = h o g. On peut immédiatement
noter que :
* la flèche c ---- 1 existe nécessairement et est
unique (1 objet terminal)
* le triangle a/c/1 commute
1(a) se trouve ainsi
en position limite pour la destruction des différences entre f et g, il en est
le co-égalisateur.
Dans un Topos
bien pointé, toute flèche de a vers 1 où a n'est isomorphe ni à 0 ni à 1 est le
co-égalisateur d'au moins une paire de flèches parallèles différentes (est
en position universelle pour la destruction de leur différence). Ou : toute
flèche de a vers 1, qui ne soit ni minimum ni maximum, apparaît comme
destructrice universelle d'une différence au moins. C'est l'envers du fait que, dans ce même Topos bien pointé, toute différence
est évaluable. J'appellerai structure dialectique d'un Topos bien pointé l'existence dans un tel Topos
d'une corrélation pensable entre la localisation des différences et la
destruction des différences par l'Un.
Si la flèche 1(a)
peut être dite le compte-pour-un de a, ce qu'exprime la structure dialectique d'un Topos
bien pointé, c'est qu'un compte-pour-un qui n'inscrit pas de différence en 1
(1(a) n'est pas un sous-objet de 1 dans ce Topos) fait-un quelque part (au sens de
faire-un de ce qui était deux). Dans un Topos bien pointé soit une flèche est immanente
à l'un,
participe à l'un (mode philosophique de l'existence d'un monomorphisme), soit
elle fait-un,
elle détruit quelque part une différence au moins (mode philosophique de
l'existence d'un co-égalisateur pour une paire de flèches parallèles), mais pas
les deux en même temps.
Algèbre de 1 (suite)
Intersection, union, complément
Nous allons définir trois opérations sur
les sous-objets de 1 : l'intersection, l'union et le complément.
Attention : nous savons qu'une
flèche a ---- 1 est déterminée (puisque unique) dès que a est fixé.
Nous emploierons donc désormais de façon équivalente pour désigner ce type de
flèche les écritures 1(a) et a; il nous arrivera de parler du sous-objet a de 1
pour désigner un monomorphisme de source a et de cible 1, pris comme représentant
d'une classe de similarité. La notation "a" comporte par conséquent
une équivoque, puisque pouvant renvoyer tant à l'objet a qu'à la flèche a ---- 1; cette équivoque a elle-même une signification, car
cette flèche est en sorte le compte-pour-un de l'objet a.
L'intersection de deux sous-objets.
Soit deux sous-objets a et b de 1.
Considérons le pullback de a et de b (il existe toujours, puisque a et b sont
deux flèches "perpendiculaires" de même cible 1). Notons a b le point-pullback, et 1(a) 1(b) la diagonale qui va du point-pullback vers 1.
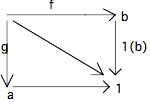
La flèche 1(a) 1(b) sera nommée l'intersection de 1(a) et
1(b).
a) 1(a) 1(b) est inférieure (pour la relation ) et à 1(a) et à 1(b). Car dans le diagramme précédent,
la flèche 1(b) o f est une flèche du point-pullback vers 1. Il n'y a qu'une
flèche de ce genre, qui est justement la flèche 1(a) 1(b). On a donc 1(b) o f = 1(a) 1(b), et par conséquent (1(a) 1(b)) 1(b).
Le même raisonnement appliqué au
triangle de gauche et à la composition 1(a) o g montre que 1(a) 1(b) est inférieur à 1(a).
b) on démontre également que 1(a) 1(b) est le plus grand (pour la relation ) des sous-objets qui sont plus petits que 1(a) et
que 1(b). Autrement dit : si un sous-objet c de 1 est tel que c a et c b, alors c (1(a) 1(b)). Ou : pour deux sous-objets quelconques de 1,
leur intersection est le plus grand des sous-objets qui leur sont simultanément
inférieurs, elle est leur PGI (plus grand des inférieurs); ce que l'on notera :
1(a) 1(b) = PGI (a,b)
L'union de deux sous-objets de 1.
Soit deux sous-objets a et b de 1.
Considérons la flèche co-produit des flèches a et b, notée, rappelons-le, a,b .
Selon un théorème (que nous ne
démontrerons pas), toute flèche dans un Topos admet une décomposition en un
épimorphisme suivi d'un monomorphisme; autrement dit : étant donnée f, il
existe m (monomorphisme) et e (épimorphisme) tels que : f = m o e. Le
monomorphisme de cette décomposition s'appelle l'image de f.
La flèche co-produit des flèches a et b
peut donc être décomposée en un épimorphisme et en son image; celle-ci sera
nommée l'union de a et de b, et sera notée a b.
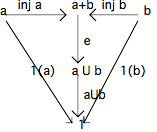
On démontre que deux sous-objets a et b
sont tous deux inférieurs à leur union. On a donc :
a a b, et b a b.
Et également que l'union a b est le plus petit des sous-objets de 1 supérieurs
simultanément à a et à b, elle est leur PPS (plus petit des supérieurs), ce que
l'on notera :
a b = PPS (a,b)
Le complément d'un sous-objet de 1.
Le complément -a d'un sous-objet a est
le sous-objet de 1 dont la centration est la négation de la centration de a.
Soit :
c(-a) = o c(a)
L'idée de complément d'un sous-objet est
donc directement référée à la centration. Il n'y a pas de possibilité, du
reste, de parler de "la négation de a" : car la négation, étant la
centration du faux, est une flèche qui va de C vers C et qui ne peut donc se
composer avec une flèche de type a --- 1. On peut soutenir que le complément de a, soit
la flèche 1(-a), est la négation "indirecte" de la flèche a :
négation médiée par la centration.
Le diagramme complet de la définition de
-a est le suivant (en deux étapes) :
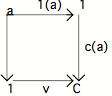 la composition de c(a), qui est une flèche de 1 vers C, et de
, qui est une flèche de C vers C, est une flèche de 1
vers C.
la composition de c(a), qui est une flèche de 1 vers C, et de
, qui est une flèche de C vers C, est une flèche de 1
vers C.
1 -----c(a) --- C --- --- C
1 --- o c(a) --- C
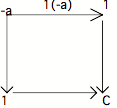
La proposition fondamentale du
complément est la suivante : L'intersection de a et de son complément -a est
similaire à 0 (0 est bien sur pris ici au sens de la flèche 0 ---- 1, qui, rappelons-le, est le minimum dans l'ordre
partiel des sous-objets de 1). Soit :
1(a) 1(-a) 1(0)
démonstration
Considérons le diagramme suivant :

Le carré du haut est le pullback qui
définit l'intersection a -a. Le carré du bas est le pullback qui définit la
centration de -a comme étant la négation de la centration de a, o c(a). En vertu du "lemme du pullback" que
nous avons déjà rencontré, le rectangle complet est un pullback :
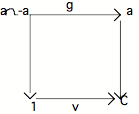
La flèche verticale de droite qui va de
a vers C est : o c(a) o a
Or, le pullback commutatif qui définit
la centration de 1(a) - ou a - permet d'écrire :
c(a) o a = v o a
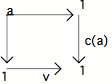
Il vient alors : o c(a) o a = o v o a
Nous savons que o v = F (définition de la négation)
Donc : o c(a) o a = F o a
Finalement, notre rectangle "mis au
carré" se présente ainsi :
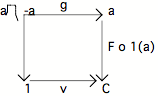
Sa commutation exige que : F o 1(a) o g
= v o 1(a -a). Notons que 1(a) o g et 1(a -a) sont deux flèches vers 1. Reportons les sur le
pullback qui définit le faux :
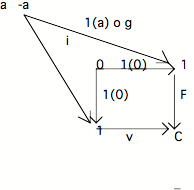
L'équation F o 1(a) o g = v o 1(a -a) exprime la commutation du "carré" extérieur.
Par conséquent, il doit exister une flèche (unique) i de a -a vers 0 qui fait commuter tout le diagramme
(définition du pullback comme limite).
En particulier, on a : 1(0) o i = 1(a -a). Ce qui, d'après la définition de la relation
d'ordre, signifie que :
1(a -a) 1(0)
Comme nous avons établi que 1(0) était
le sous-objet minimum pour la relation , le sous-objet 1(a -a) ne saurait être plus petit que 1(0) et l'équation
précédente signifie forcément que 1(a -a) est en fait le même sous-objet que 1(0), donc que
1(a -a) est similaire à 1(0). CQFD
On peut aussi écrire : PGI(a,-a) 0 (puisque nous avons montré que l'intersection de
deux sous-objets est le plus grand de tous les sous-objets simultanément plus
petits que chacun d'entre eux). Ce qui signifie que le seul sous-objet de 1 qui
soit simultanément inférieur à a et à -a est 0, qui est de toutes façons
inférieur à tous, étant le minimum pour la relation d'ordre.
La proposition 1(a -a) 1(0) est équivalente, dans le domaine des relations logiques, à : p -p = F. Elle est l'énoncé du principe de
non-contradiction en termes de sous-objets de 1.
Dans le livre Gamma de la Métaphysique, Aristote pose trois grands principes de la logique :
le principe d'identité (a a), le principe de non-contradiction (a -a 0), et le principe du tiers exclu (p -p = v).
Le principe de non-contradiction est un principe logique
universel, car vrai pour tout Topos; il régit tout univers possible (ce qui,
soit dit entre parenthèses, est la conception de Leibniz). Le principe du tiers
exclu, dont la transposition en termes de sous-objets donnerait : a -a 1, n'est, quant à lui, valide que dans certains Topos
(comme le Topos des ensembles), mais pas dans d'autres (la démonstration de
l'équation a -a 1 est impossible, ce n'est pas un théorème). Le principe
du tiers exclu requiert autre chose que la simple définition d'un univers
possible, il est une propriété singulière de certains Topos. On dira d'un Topos
qui valide le principe du tiers exclu, qu'il est un Topos booléen.
Dans un Topos non booléen, la négation
est affaiblie, car ce qui est obtenu quand une chose est niée, à savoir le
complémentaire, n'y est pas exactement "tout ce qui n'est pas" cette
chose; quelque chose persiste à s'affirmer (ou témoigne d'un affirmatif
irréductible, inentamé), qui n'a pas été touché par la négation. On reconnaît
le voisinage avec les conceptions freudiennes de la négation (désaveu, déni
etc...). Ou en termes lacaniens : quand la négation n'est pas strictement
booléenne, il y a du "pas-tout". Ou encore : la Femme est ce qui
décomplète la logique classique. Ou encore : la Femme est intuitionniste (ce
qui est dit depuis longtemps, par ailleurs). Et enfin : il est requis que
l'espace toposique soit non booléen pour pouvoir énoncer qu'il n'y a pas de
rapport sexuel.
––––––––––